4.7: Perfiles de velocidad

Introducción

Ya se ha visto que el perfil de la velocidad del fluido local promedio en el tiempo\(\overline{u}\) desde la parte inferior a la superficie en flujo turbulento hacia abajo de un plano es mucho más contundente en la mayor parte de la profundidad de flujo que el perfil parabólico correspondiente para flujo laminar (Figura 4.3.1). Este es el lugar para amplificar y cuantificar el tratamiento de los perfiles de velocidad en flujos turbulentos de capa límite.

Primero plantearé la siguiente pregunta: ¿Se puede encontrar una ecuación para el perfil de velocidad en un flujo turbulento de capa límite escribiendo una ecuación como la Ecuación 1.3.6 para flujo turbulento y resolviendo para el perfil de velocidad por integración? Como se señaló anteriormente, la Ecuación 4.2.4, para la distribución del esfuerzo cortante total en el flujo, es válida tanto para el flujo turbulento como para el flujo laminar, ya que no se hicieron suposiciones sobre la naturaleza de los movimientos internos del fluido en su derivación, solo que el flujo debe ser estable y uniforme en el promedio. Y una expresión del mismo tipo que la Ecuación 1.3.6, que define el esfuerzo cortante, también se puede escribir para flujo turbulento:

\[\tau=\mu \frac{d u}{d y}+\eta \frac{d u}{d y} \label{4.12} \]

El término\(\mu(d u / d y)\) es el esfuerzo de cizallamiento viscoso debido a la cizalladura media a través de planos paralelos al límite. (En realidad, es un promedio espacial sobre un área de tal plano que es grande en relación con las escamas de Foucault, porque el cizallamiento del fluido varía de punto a punto en flujo turbulento). El término\(\eta(d u / d y)\) es una forma de escribir el esfuerzo de cizallamiento turbulento a través de estos planos que involucra una cantidad artificial\(\eta\), llamada viscosidad de Foucault, que es formalmente como la viscosidad molecular\(\mu\). En todas partes en un flujo de cizallamiento turbulento excepto muy cerca del límite sólido, la viscosidad de Foucault es mucho mayor que la viscosidad molecular, porque el transporte de momento turbulento es dominante sobre el transporte de momento molecular. (A menudo\(\eta\) se escribe como\(\rho \varepsilon\), donde se\(\varepsilon\) puede ver como la viscosidad cinemática de Foucault, en analogía con\(ν\); también\(\varepsilon\) se llama el coeficiente de difusión de Foucault.) Al igual que para el flujo laminar, las expresiones para\(\tau_{\text{o}}\) en la Ecuación\ ref {4.12} y la Ecuación 1.3.6 se pueden establecer iguales para dar una ecuación diferencial para\(u\) como una función de la distancia\(y\) desde el límite:

\[(\mu+\eta) \frac{d u}{d y}=\gamma \sin \alpha(d-y) \label{4.13} \]

Desafortunadamente siempre hay un problema insuperable en la integración de la Ecuación\ ref {4.13}, o cualquier otra ecuación como ésta para flujo turbulento en un conducto o canal con alguna otra geometría, para encontrar la distribución de velocidad. A diferencia de la viscosidad molecular\(\mu\), la viscosidad de Foucault\(\eta\), más que ser una propiedad del fluido, depende del flujo: varía con la altura por encima del límite, porque el esfuerzo de cizallamiento turbulento que representa es una función del flujo en sí, para lo cual estamos tratando de resolver. Por lo tanto, siempre estamos obligados a encontrar la distribución de velocidad en flujo turbulento por experimento.

Es importante darse cuenta, sin embargo, que los experimentos para encontrar el perfil de velocidad no tienen que ser ciegamente empíricos: el razonamiento físico puede ser utilizado para adivinar qué efectos y por lo tanto qué variables son importantes para gobernar la distribución de velocidad en las diversas capas del flujo. Si las relaciones funcionales así especificadas por la estructura dimensional del problema son consistentes con los resultados observacionales, entonces se confirma la corrección de esa visión cualitativa de la física. De hecho, gran parte de lo que se sabe sobre el flujo turbulento más allá de los límites sólidos se ha aprendido de esta manera.

Nos quedaremos con un flujo constante y uniforme hacia abajo por un plano, pero exactamente el mismo tipo de análisis podría hacerse para el flujo en un conducto cerrado. Piensa en qué variables tienes que especificar para tener plenamente en cuenta el perfil de la velocidad promedio en el tiempo u a lo largo de una línea imaginaria a través del flujo, normal al límite inferior, que se extiende desde la parte inferior hasta la superficie libre (Figura\(\PageIndex{1}\)).

Figura\(\PageIndex{1}\): Croquis de definición para el análisis dimensional de perfiles de velocidad en flujo turbulento de canal abierto.

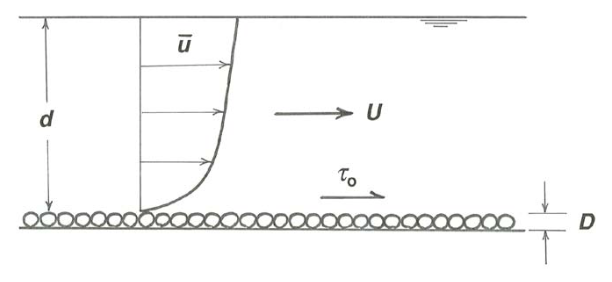
El fondo puede ser liso o rugoso. Al igual que en el problema de la resistencia al flujo, hacer la suposición (no buena, pero nos pone en marcha) que la rugosidad se puede caracterizar por el tamaño\(D\) de los elementos sin tener que preocuparse por su forma y disposición. El esfuerzo cortante límite\(\tau_{\text{o}}\) es la mejor variable a utilizar para caracterizar la resistencia del flujo. Debe esperar que en general también se necesite la profundidad\(d\) de flujo. \(\mu\)Se necesita la viscosidad, ya que está atada con cizallamiento en el fluido. Finalmente, como en todos los problemas en el flujo turbulento,\(\rho\) se necesita la densidad del fluido, porque el fluido experimenta aceleraciones locales (en forma de remolinos), por lo que la inercia del fluido es importante. Por lo tanto, se\(\overline{u}\) puede ver como una función de\(\tau_{\text{o}}\),\(\rho\),\(\mu\), y\(d\), y\(D\), por supuesto, la distancia por\(y\) encima de la parte inferior:

\[\overline{u}=f\left(\tau_{0}, \rho, \mu, D, d, y\right) \label{4.14} \]

La relación funcional adimensional para\(\overline{u}\) es entonces

\[\frac{\overline{u}}{u .}=f\left(\frac{u_{*} D}{v}, \frac{d}{D}, \frac{y}{d}\right) \label{4.15} \]

donde hemos hecho uso de la velocidad de cizallamiento\(u_{*}\) y la viscosidad cinemática\(ν\) introducidas anteriormente en este capítulo. La ecuación\ ref {4.15} dice que\(\overline{u} /u_{*}\), una versión adimensional de\(\overline{u}\) (a menudo denotada\(u^{+}\)), debe ser una función únicamente del número de rugosidad de Reynolds\(u_{*}D/ν\) y la rugosidad relativa\(d/D\) para una posición adimensional dada\(y/d\) en el flujo. Existen posibilidades alternativas para las tres variables adimensionales independientes (por ejemplo, las tres podrían ponerse en forma de un número de Reynolds, cada una con una diferente de las tres variables de longitud), pero esta es la más natural.

Estoy seguro de que todos los datos de velocidad que podrías tener en tus manos se trazarían muy bien en una gráfica de cuatro dimensiones usando las variables\(\overline{u} /u_{*}\),\(u_{*}D/ν\),\(d/D\), y\(y/d\). Pero a pesar de que el número de variables se ha reducido de siete a cuatro, seguiría teniendo un trabajo de trazado oneroso y un producto que sería difícil de manejar para su uso práctico. Además, sería necesario un estudio más cuidadoso para descifrar lo que el gráfico le dice sobre la física detrás de los perfiles de velocidad. Este es un buen lugar para pensar si el problema puede simplificarse aún más mediante un enfoque de dividir y conquistar en el que algunas de las variables son eliminadas o modificadas en ciertos rangos de condiciones para llegar a funciones más simples que representen bien los datos bajo esas condiciones. Esto tiene dos propósitos: proporciona resultados útiles, y ayuda a aclarar los efectos físicos que son importantes.

En primer lugar, en las dos secciones siguientes, presentaré algunas ideas sobre la energía en flujo turbulento. Esto puede parecer fuera de lugar aquí, pero lleva a dos conclusiones que son de gran importancia para los perfiles de velocidad en flujo turbulento: la de

1. la existencia de capas internas y externas superpuestas del flujo, en las que se mantienen ecuaciones separadas para perfiles de velocidad, y la de
2. la independencia aproximada de estos perfiles en el número de Reynolds de flujo medio.

Otras subsecciones están dedicadas a los detalles de los perfiles de velocidad en las capas interna y externa de los flujos para los cuales el diámetro del sedimento en el lecho es mucho menor que la profundidad de flujo.

Energía

Al hacer algunas suposiciones simplificadoras, ayuda a echar un vistazo más de cerca a la naturaleza de la turbulencia en un flujo de canal. Voy a presentar algunos argumentos que espero tengan algún sentido para ustedes aunque no se puedan desarrollar rigurosamente aquí. En lo que sigue, recuerda que la energía cinética, una cantidad\(m v^{2} / 2\) asociada a un cuerpo con masa que se\(m\) mueve con velocidad\(v\), se cambia solo cuando una fuerza desequilibrada sí trabaja en el cuerpo, y el cambio en la energía cinética es igual al trabajo realizado. El cambio en la energía cinética causado por la acción de ciertas fuerzas como la gravedad puede ser recapturado sin ninguna pérdida de energía mecánica, pero el trabajo realizado por las fuerzas de fricción representa la conversión de la energía mecánica en calor.

Comenzaré con el flujo laminar porque la contabilidad energética es más sencilla (Figura\(\PageIndex{2}\) A). El esfuerzo cortante viscoso que actúa a través de los planos de cizallamiento funciona contra el fluido en movimiento. (Recuerde que una fuerza sí funciona sobre un cuerpo en movimiento siempre que haya un componente de la fuerza en la dirección de movimiento del cuerpo, como es el caso aquí.) El esfuerzo de cizallamiento viscoso es el mecanismo que convierte la energía potencial en calor, siendo el calor luego transferido al entorno por conducción o radiación. La magnitud particular de la energía cinética en el flujo en el proceso de esta conversión es un resultado de la dinámica del flujo.

Figura\(\PageIndex{2}\): Energética de A) flujo laminar de canal abierto y B) flujo turbulento de canal abierto.

En el flujo turbulento (Figura\(\PageIndex{2}\) B), la energía cinética está contenida no solo en el flujo medio sino también en las fluctuaciones turbulentas. La energía potencial se convierte nuevamente en calor, pero la forma en que el flujo media esta conversión, y por lo tanto la imagen de la energía cinética en el flujo, es más complicada. Esto se debe a que la energía se extrae principalmente por el trabajo realizado contra el movimiento medio por el esfuerzo de cizallamiento turbulento en lugar de por el esfuerzo viscoso, ya que en todos los niveles del flujo excepto muy cerca del fondo, el primero ensombrece en gran medida al segundo. Este trabajo realizado por el esfuerzo de cizallamiento turbulento transforma la energía cinética del movimiento medio en energía cinética asociada principalmente con los remolinos más grandes, que tienen el papel dominante en el esfuerzo de cizallamiento turbulento porque son los portadores de mayor alcance de impulso de fluido. Pero no gran parte de esta energía cinética turbulenta se convierte directamente en calor en estos grandes remolinos, porque son tan grandes en relación con las diferencias de velocidad a través de ellos que las tasas de cizallamiento en ellos son muy pequeñas.

Entonces, ¿a dónde va la energía cinética? Respuesta: se dicta a remolinos más pequeños. Esta frase “dictada” podría parecerte plausible pero poco iluminadora. Los remolinos grandes degeneran o se distorsionan en remolinos más pequeños de formas no elaboradas aquí, y cuando esto sucede, la energía cinética que se asoció con los remolinos grandes se “transfiere a” (es decir, ahora se asocia con) los remolinos más pequeños. Pero todas las probabilidades están en contra de que los remolinos más pequeños se organicen nuevamente en remolinos más grandes, solo observe la ruptura del flujo regular en un penacho de humo para tener la sensación de que la tendencia natural en los movimientos turbulentos es que los movimientos a mayor escala se dividan en movimientos a menor escala. Entonces, en términos de energía cinética, la turbulencia es en gran parte una calle unidireccional: pasa energía principalmente de escalas grandes a escalas pequeñas, no en la otra dirección. Este efecto se llama cascada de energía. Las tasas de cizallamiento son mayores en los remolinos más pequeños debido a su pequeño tamaño en relación con las diferencias de velocidad entre ellos, y es en estos remolinos más pequeños donde la mayor parte de la energía cinética finalmente se convierte en calor. De hecho, la razón por la que existe un límite inferior para el tamaño de Foucault es que por debajo de cierta escala las tensiones de cizalladura viscosas son tan fuertes que amortiguan las fluctuaciones de velocidad.

Una consecuencia muy significativa es que la viscosidad tiene un efecto directo sobre la turbulencia solo en las escalas más pequeñas de movimiento turbulento. Si se incrementa el número de Reynolds de flujo medio, la cascada de energía se alarga en las escalas más pequeñas mediante el desarrollo de remolinos aún más pequeños, pero la estructura de turbulencia a escalas mayores no cambia mucho (Figura\(\PageIndex{3}\)). Entonces, cualquier característica de volumen del flujo que se rige por la turbulencia a gran escala, como el perfil de velocidad, que depende principalmente del intercambio turbulento del momento de fluido, debería ser solo ligeramente dependiente del número de Reynolds. Este efecto se llama similitud de números de Reynolds-number.

Figura\(\PageIndex{3}\): Incremento en el rango de escamas de Foucault en función del número de Reynolds de flujo medio.

Capas internas y externas

Ahora volvemos a los perfiles de velocidad. Quiero convencerte de que se pueden reconocer dos regiones o capas diferentes pero superpuestas del flujo (Figura\(\PageIndex{4}\)) en las que el perfil de velocidad no depende de la lista completa de variables\(\tau_{\text{o}}\),\(\rho\),\(\mu\),,\(D\)\(y\), y\(d\) se usa en el análisis dimensional arriba pero en ciertos subconjuntos. La ventaja es que en cada una de estas capas existe entonces una relación funcional más simple para el perfil de velocidad, una que conduce a una curva en una gráfica bidimensional que sostiene muy bien para casi todo el rango de flujos de canal turbulentos. Agitaré un poco los brazos sobre las diversas variables, pero claro que la evidencia más convincente es que así es como funcionan las cosas realmente, como verán.

Cerca del límite inferior, en lo que llamé la zona de amortiguamiento y por caminos fuera de ella, la turbulencia es a pequeña escala e intensa, y tanto la producción como la disipación de energía cinética turbulenta se sabe a partir de mediciones reales que están en un pico. Es razonable ver la dinámica de la turbulencia, y por lo tanto la naturaleza del perfil de velocidad, como controlada por efectos locales y sustancialmente independiente de la naturaleza de la turbulencia en el resto del flujo, hasta la superficie libre. Esto también es cierto para la subcapa viscosa, si hay una presente, porque allí el perfil de velocidad es controlado por el fuerte cizallamiento viscoso adyacente al límite sólido. Por lo tanto, el perfil de velocidad en esta capa interna depende de\(\tau_{\text{o}}\)\(D\)\(\rho\),\(\mu\),, y\(y\), pero no de\(d\).

Figura\(\PageIndex{4}\): Capas en flujo turbulento de canal abierto.

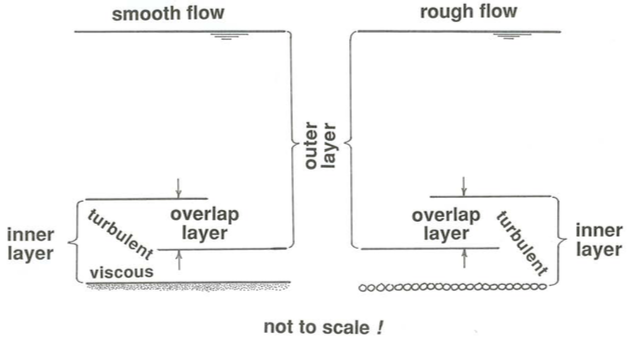
Por otro lado, sobre la mayor parte de la profundidad de flujo, desde la superficie libre hasta la parte superior de la capa tampón en flujo suave, ya se ha visto en la discusión de la energía turbulenta que el perfil de velocidad debería ser en gran medida independiente de\(\mu\). Si el límite es rugoso, el perfil debe ser independiente, así\(D\) como de\(\mu\) abajo a una posición lo suficientemente lejos por encima de los elementos de rugosidad que la turbulencia arrojada por los elementos no sea importante en la dinámica de turbulencia. Pero debes esperar que el perfil dependa\(d\), porque el tamaño de los remolinos más grandes es proporcional a la profundidad del flujo. El perfil de velocidad en esta capa externa (aquí he generalizado la significación del concepto de capa externa introducido en una sección anterior) debería depender así de\(\tau_{\text{o}}\),\(\rho\),\(d\), y\(y\), pero no de\(D\) o\(\mu\).

Si escudriña las definiciones de las capas interna y externa en los dos últimos párrafos a la luz de lo que he dicho sobre la estructura del flujo, verá que es probable que se superpongan. En otras palabras, hay una zona donde el perfil de velocidad es al mismo tiempo independiente de las tres variables\(d\),\(\mu\), y\(D\). Esto debería ser cierto siempre que el número de Reynolds de flujo medio sea lo suficientemente alto (mucho más allá de la transición laminar-turbulenta) como para que la zona dominada por la viscosidad cerca del límite sea muy delgada en relación con la profundidad de flujo. (Recuerde que el grosor de la subcapa viscosa disminuye a medida que aumenta el número de Reynolds, debido a que el número de Reynolds es una medida de la importancia relativa de las fuerzas inerciales y las fuerzas viscosas).

Probablemente ya estás pensando que te he presentado una confusión de capas. Los voy a resumir en este punto. Por un lado, en términos de la importancia relativa del esfuerzo de cizallamiento viscoso y el esfuerzo de cizallamiento turbulento, es natural reconocer tres zonas de intercalación pero bien definidas (la subcapa viscosa, la capa amortiguadora y la capa externa) o, más generalmente, una capa dominada por la viscosidad por debajo y una turbulencia- capa dominada arriba. Por otro lado, en términos de importancia o falta de importancia de las variables (una materia relacionada pero no idéntica), se pueden reconocer dos capas superpuestas: una capa interna en la que la velocidad media, y otras características medias del flujo también, dependen de\(\mu\) o\(D\) (o ambas) pero no\(d\), y la misma capa exterior en la que la velocidad media depende de\(d\) pero no de\(\mu\) o\(D\). En el flujo aproximado, todo el grosor del flujo está dominado por la turbulencia, y no hay ninguna capa dominada por la viscosidad, pero todavía hay capas internas y externas.

La Ley del Muro para Límites Lisos

Observe primero el perfil de velocidad de la capa interna sobre un límite inferior físicamente liso. Por lo que se acaba de decir sobre la capa interna,

\[\overline{u}=f\left(\tau_{0}, \rho, \mu, y\right) \label{4.16} \]

o en forma adimensional,

\[\frac{\overline{u}}{u}=f\left(\frac{\rho u_{*} y}{\mu}\right) \label{4.17} \]

La ecuación\ ref {4.17} establece que la velocidad\(u\), no dimensionalizada usando\(u_{*}\), depende únicamente de\(y^{+}\), la distancia adimensional desde la parte inferior. Por lo tanto, el perfil de velocidad debe ser expresable como una sola curva para todos los flujos de canales turbulentos con límites inferiores suaves. La ecuación\ ref {4.17} es la forma general de lo que se llama la ley del muro para límites lisos.

Debe esperar que el perfil de velocidad expresado en la Ecuación\ ref {4.17} esté en dos partes, una correspondiente a la subcapa viscosa y la otra a la parte externa de la capa interna, donde la tensión de cizallamiento turbulenta predomina sobre la tensión de cizallamiento viscosa. Estas dos partes del perfil tienen que pasar suavemente una de la otra en la capa intermedia intermedia. Debido a que las aceleraciones de fluidos no son importantes en la subcapa viscosa\(\tau_{\text{o}}\), depende de\(\mu\), y\(y\), pero no de\(\rho\):\(u\)

\[\overline{u}=f\left(\tau_{0}, \mu, y\right) \label{4.18} \]

La única manera de escribir la ecuación\ ref {4.18} en forma adimensional es

\[\frac{\mu u}{\tau_{o} y}=\mathrm{const} \label{4.19} \]

porque solo hay una manera de formar una variable adimensional a partir de las cuatro variables\(\overline{u}\),\(\tau_{\text{o}}\),\(\mu\), y\(y\). La ecuación\ ref {4.19} se puede hacer malabarismos algebraicamente un poco introduciendo\(\rho\) en ambos lados, sin otra razón que ponerla en la misma forma que la Ecuación\ ref {4.17}:

\[\frac{\overline{u}}{u_{*}}=\mathrm{const} \frac{\rho u_{*} y}{\mu} \label{4.20} \]

La constante en la Ecuación\ ref {4.20} resulta ser la unidad. Para tener una idea de por qué, volver a la Ecuación 4.2.7, la solución exacta para el perfil de velocidad en el flujo de canal laminar. Es razonable esperar que el perfil de velocidad en la subcapa viscosa de un flujo de canal turbulento sea como el perfil de velocidad cerca del límite en un flujo de canal laminar. Los puntos cercanos al límite en flujo laminar, donde el gradiente de velocidad\(d\overline{u} /dy\) es muy grande, están muy alejados en la extremidad de la parábola en la Ecuación 4.2.7, por lo que el segundo término a la derecha en la Ecuación 4.2.7 se puede descuidar y\(u\) asumir que es una función lineal de\(y/d\):

\[\overline{u}=\frac{\tau_{o}}{\mu d}(y d) \label{4.21} \]

Cuando se lanza en la misma forma que la Ecuación\ ref {4.20}, esto se convierte en

\[\frac{\overline{u}}{u_{*}}=\frac{\rho u_{*} y}{\mu} \label{4.22} \]

La ecuación\ ref {4.22} representa la parte específica de la ley de la pared para un flujo dinámicamente suave dentro de la subcapa viscosa. La figura\(\PageIndex{5}\) muestra que la Ecuación\ ref {4.22} está en buena concordancia con las medidas cuidadosas de la velocidad en la subcapa viscosa.

Figura\(\PageIndex{5}\): Gráfica de velocidad de flujo promedio adimensional\(\overline{u} / u_{*}\) vs. distancia adimensional desde el límite\(\rho u_{*} y / \mu\), para la subcapa viscosa en flujo turbulento de canal abierto. Esta parcela representa la ley del muro dentro de la subcapa viscosa.

En la parte externa, dominada por turbulencias de la capa interna sobre un fondo físicamente liso, podemos suponer que\(d\overline{u}/ dy\) no depende\(\mu\), porque el esfuerzo cortante y por lo tanto el gradiente de velocidad se determina casi en su totalidad por el intercambio de momento turbulento (ver Ecuación\ ref {4.12}). Por otro lado,\(u\) sí mismo debe depender de\(\mu\), porque el perfil de velocidad en la parte dominada por turbulencias de la capa interna debe estar conectado al de la parte dominada por la viscosidad, y usted acaba de ver que depende el perfil de velocidad en la subcapa viscosa\(\mu\). En otras palabras, la velocidad en la base de la parte dominada por turbulencias de la capa interna depende de la velocidad en la parte superior de la subcapa viscosa, que a su vez depende de\(\mu\). La parte dominada por la viscosidad del perfil puede verse como “anclando” la parte dominada por turbulencias del perfil al fondo, donde la velocidad es cero por la condición de antideslizante. Entonces, para obtener el perfil de velocidad tenemos que comenzar con el gradiente de velocidad, en lugar de la velocidad misma, y escribir\(d \overline{u} / d y y = f\left(\tau_{0}, \rho, y\right)\) en forma adimensional como

\[\frac{y}{u_{*}} \frac{d u}{d y}=A \label{4.23} \]

donde\(A\) es una constante adimensional que debe mantenerse en esta capa particular para todos los flujos de canales turbulentos sobre límites suaves, y luego integrarse para obtener el perfil de velocidad adimensional:

\[\frac{\overline{u}}{u_{*}}=A \ln y+A_{1} \label{4.24} \]

donde\(A_{1}\), también adimensional, es una constante de integración. Por el concepto de similitud de número de Reynolds discutido anteriormente,\(A\) debe ser casi constante siempre que el número de Reynolds sea lo suficientemente alto como para que la turbulencia se desarrolle completamente.

Obsérvese que la Ecuación\ ref {4.24} no contiene\(\mu\) explícitamente, sino de lo dicho anteriormente,\(\mu\) tiene que estar ahí en alguna parte. La resolución de esta aparente paradoja es que la constante de integración\(A_{1}\) debe depender de ella\(\mu\). Puedes verificar que esto es así señalando que la Ecuación\ ref {4.24} se puede poner en la forma general de la ley del muro dada por la Ecuación\ ref {4.17} si y solo si\(A_{1}\) es igual a\(A \ln \left(\rho u_{*} / \mu\right)+B\): poniendo esta expresión for\(A_{1}\) en la Ecuación\ ref {4.24},

\(\frac{\overline{u}}{u_{*}}=A \ln y+A \ln \frac{\rho u_{*}}{\mu}+\mathrm{B}\)

\[=A \ln \frac{\rho u_{*} y}{\mu}+B \label{4.25}\]

La constante\(B\) es solo el residuo de la constante de integración después de haber\(A \ln \left(\rho u_{*} / \mu\right)\) sido extraída.

No hay acuerdo universal en la literatura sobre los valores de las constantes\(A\) y\(B\): generalmente\(A\) se toma como entre\(2.4\) y\(2.5\), y\(B\) se toma como entre\(5\) y\(6\). Las pequeñas diferencias\(A\) y las mayores diferencias\(B\) de fuente a fuente son un resultado comprensible del ajuste de líneas rectas en parcelas semilogarítmicas de datos ligeramente dispersos de diversos estudios experimentales. Las discusiones sobre los valores de estas constantes se pueden encontrar en Monin y Yaglom (l971) y Hinze (1975). Con los valores comúnmente utilizados\(A = 2.5\),\(B = 5.1\), Ecuación\ ref {4.25} se convierte

\[\frac{\overline{u}}{u_{*}}=2.5 \ln \frac{\rho u_{*} y}{\mu}+5.1 \label{4.26} \]

La constante\(A\), que es un reflejo de la naturaleza del transporte de impulso turbulento en la capa interna, a menudo se escribe 1\(/ \kappa\), y\(\kappa\) se llama la constante de von Kármán. Así,\(\kappa\) tiene un valor muy cercano\(0.4\). La razón\(A\) está escrita como\(1/\kappa\) es histórica, no fundamental. Además, se debe esperar una dependencia débil del\(A\) número de Reynolds de flujo medio. La naturaleza exacta de la variación\(A\) con el número de Reynolds, y con la concentración de sedimentos suspendidos en los flujos de transporte de sedimentos también, ha sido polémica.

La ecuación\ ref {4.26} muestra que el perfil de velocidad se expresa mediante una sola curva para la parte dominada por turbulencias de la capa interna, tal como fue el caso de la parte dominada por la viscosidad. Es el perfil dado por la Ecuación\ ref {4.26} que suele llamarse la ley de la pared, aunque ese término describe más adecuadamente todo el perfil de capa interna, dominado por la viscosidad y dominado por turbulencias, más la transición entre.

Figura\(\PageIndex{6}\): Gráfica de velocidad de flujo promedio adimensional\(\overline{u} / u_{*}\) vs. distancia adimensional desde el límite\(\rho u_{*} y / \mu\), para la capa interna sobre un límite suave en flujo turbulento de canal abierto. Esta gráfica representa la ley del muro para un flujo dinámicamente suave.

Figura\(\PageIndex{6}\).

En resumen, la velocidad promedio de tiempo\(u\) en la capa interna sobre un límite suave, cuando no se dimensiona dividiendo por\(u_{*}\), debe graficarse como una sola curva en función de\(y^{+}\), la distancia adimensional por encima de la parte inferior. La Figura\(\PageIndex{6}\), que incorpora los datos ya trazados en la Figura\(\PageIndex{5}\) para la subcapa viscosa, muestra el perfil de velocidad a través de toda la capa interna sobre un límite liso. Este perfil representa la ley completa del muro para contornos lisos. Los puntos de datos en la parte dominada por viscosidad de la capa interna siguen la Ecuación\ ref {4.22}; los puntos de datos en la parte dominada por turbulencias de la capa interna siguen la Ecuación\ ref {4.26}, que se traza aquí como una línea recta debido a las coordenadas semilogarítmicas.

Entre\(y^{+}\) los valores de aproximadamente\(5\) y aproximadamente\(30\) en la Figura\(\PageIndex{6}\) hay una transición suave entre el perfil dominado por viscosidad (Ecuación\ ref {4.22}) y el perfil dominado por turbulencias (Ecuación\ ref {4.26}); ver Figura\(\PageIndex{7}\). Esta es la capa amortiguadora, donde tanto el esfuerzo cortante viscoso como el esfuerzo cortante turbulento son importantes. Para\(y^{+} < 5\) el esfuerzo cortante turbulento es insignificante, y la Ecuación\ ref {4.22} describe el perfil; para\(y^{+} > 30\) el esfuerzo cortante viscoso es insignificante, y la Ecuación\ ref {4.26} describe el perfil. Es en las gráficas de ley mural como Figura\(\PageIndex{6}\) donde los límites inferior y superior de la capa tampón se manifiestan con mayor claridad. Verás una variedad de\(y^{+}\) valores limitantes inferiores y superiores mencionados en la literatura; esto es comprensible, porque la divergencia de las curvas dadas por las Ecuaciones\ ref {4.22} y\ ref {4.26} a partir del perfil real es gradual. Aunque no es de gran significación física, la altura de intersección de las Ecuaciones\ ref {4.22} y\ ref {4.26} en la capa de búfer está en\(y^{+} = 11\), como se puede ver en la Figura\(\PageIndex{6}\). Lo que es de mayor importancia es que el esfuerzo de cizallamiento turbulento y el esfuerzo de cizallamiento viscoso se encuentran experimentalmente iguales a un\(y^{+}\) valor ligeramente mayor de aproximadamente\(12\); esto es en cierto sentido el “medio” de la capa amortiguadora.

La altura adimensional\(y^{+}\) sobre el límite en la que\(\overline{u} / u_{*}\) comienza a desviarse de la ley de la pared depende del número de Reynolds de flujo medio\(\text{Re}\); varía hacia arriba de alrededor\(500\) en pequeño\(\text{Re}\)\(1000\) a más grande\(\text{Re}\). Para\(y^{+}\) mayor que esto,\(\overline{u} / u_{*}\) es mayor de lo que predice la ley del muro.

¿Qué tan gruesa es la capa interna? El límite superior de\(y^{+}\) para la ley de la pared a números altos de Reynolds para flujo de canal abierto no está bien establecido, pero asume un\(y^{+}\) valor de\(1000\) en un flujo de agua a temperatura ambiente 1 de\(\mathrm{m}\) profundidad a una velocidad de flujo media de 0.5\(\mathrm{m} / \mathrm{s}\). Entonces\(y\) en el límite exterior de la capa interna es de aproximadamente 5\(\mathrm{cm}\). (Para resolver esto, compute\(\text{Re}\), use la curva de flujo suave en la Figura 4.6.7 para obtener\(f\) y por lo tanto\(\tau_{\text{o}}\), y poner eso en\(y^{+}\).) Por lo que la capa interna ocupa sólo un pequeño porcentaje de la profundidad de flujo, no más de\(10-20 \%\). Y la subcapa viscosa en este flujo tiene sólo una fracción de milímetro de espesor. Obsérvese que el eje logarítmico de abscisas en parcelas como Figura abscisa\(\PageIndex{6}\) multiplica toda la capa externa, en la que la Ecuación\ ref {4.26} ya no se sostiene, en una pequeña parte de la gráfica.

La mayoría de los puntos de datos en la Figura\(\PageIndex{6}\) provienen de flujos en tuberías circulares y conductos rectangulares en lugar de flujos de canal abierto. Pero los datos de los flujos de canal abierto, y de las capas límite que se desarrollan en placas planas también, son consistentes con los del flujo en tuberías y conductos. Esto enfatiza el punto importante que sostiene la ley del muro para una amplia variedad de geometrías de flujo de capa externa. De la discusión anterior de variables importantes en las capas interna y externa, esto no debería sorprender: el flujo en la capa interna se rige por efectos locales y es independiente de la naturaleza del flujo externo. De hecho, la ley del muro es aún más general: aunque aquí no vamos a perseguir el asunto, la ley del muro se mantiene incluso cuando hay un gradiente de presión sustancial (negativo o positivo) en la dirección del flujo, lo que resulta en una aceleración o desaceleración aguas abajo.

La ley del muro para las fronteras ásperas

En muchos flujos turbulentos de capa límite, el límite no es físicamente liso sino que está ocupado por, o está cubierto por, o consiste en, elementos de rugosidad de algún tipo. Por el término elemento de rugosidad me refiero a cualquier parte local del límite que sobresalga por encima de la superficie límite total o promedio. Cosas como edificios, árboles, cultivos, personas, olas de agua, partículas de arena, rocas o escamas de corrosión vienen fácilmente a la mente. En lo que sigue, asumiremos (Figura\(\PageIndex{8}\)) que los elementos de rugosidad son mucho menores que la profundidad de flujo\((D << d)\) y que la capa del flujo que consideraremos, por ahora, tiene un espesor que no es una fracción grande de la profundidad de flujo\((y << d)\). Siempre que los elementos de rugosidad no sean mucho menores que el grosor de la subcapa viscosa, el perfil de velocidad en la capa límite depende del tamaño, forma y disposición de los elementos de rugosidad, así como de\(\tau_{\text{o}}\)\(\rho\),\(\mu\), y\(y\):

\[\overline{u}=f\left(\tau_{o}, \rho, \mu, y, \text { roughness geometry) }\right. \label{4.27} \]

donde la geometría de rugosidad se especifica por la distribución de tamaños, la distribución de formas y el empaque o disposición en vista de planta de los elementos de rugosidad.

Figura\(\PageIndex{8}\): Croquis de definición para el análisis de perfiles de velocidad media en flujo dinámicamente áspero.

Para hacer cualquier progreso tenemos que ser específicos sobre la naturaleza de la rugosidad. Supongamos aquí que la rugosidad está compuesta por partículas de sedimentos minerales bastante bien clasificadas con el rango natural habitual de forma y redondez de las partículas, y que las partículas forman un lecho sedimentario completo que es plano a gran escala. La rugosidad de este tipo, denominada rugosidad granular apretada por los dinamistas de fluidos, se caracteriza bastante bien por la variable única\(D\), el tamaño medio o mediano de partícula. Esta rugosidad es del tipo mejor estudiado, y es importante en muchos flujos de agua natural sobre sedimentos, pero hay muchos otros tipos de rugosidad, tanto en la naturaleza como en la tecnología.

Con las simplificaciones anteriores, la ecuación\ ref {4.27} se convierte en

\[\overline{u}=f\left(\tau_{0}, \rho, \mu, y, D\right) \label{4.28} \]

o, en forma adimensional,

\[\frac{\overline{u}}{u_{*}}=f\left(\frac{\rho u_{*} y}{\mu}, \frac{\rho u_{*} D}{\mu}\right) \label{4.29} \]

Entonces, para el flujo sobre límites aproximados, la velocidad adimensional\(u/u_{*}\) generalmente depende no solo del número de Reynolds,\(y^{+}\) sino también del límite. La ecuación\ ref {4.28}, que también podría escribirse usando\(y/D\) en lugar de\(\rho u_{*} D / \mu\), se llama la ley del muro para límites granular-rugosos.

Dos aspectos diferentes del efecto de la rugosidad sobre el perfil de velocidad se hacen evidentes al examinar la Ecuación\ ref {4.29}. En primer lugar, es importante el tamaño de los elementos de rugosidad en relación con el grosor de la subcapa viscosa. Recuerde de la sección sobre flujo suave y flujo rugoso anterior en este capítulo que si\(D\) es mucho menor que la escala\(\mu/\rho u_{*}\) de longitud viscosa los elementos de rugosidad están incrustados en la subcapa viscosa, mientras que si\(D\) es mucho mayor que no\(\mu / \rho u_{*}\) hay subcapa viscosa y la los elementos de rugosidad están envueltos en turbulencias generadas por la separación de flujo alrededor de los elementos aguas arriba. Debe sospechar, entonces, que para muy pequeños\(\rho u_{*} D / \mu\) (menos de aproximadamente\(5\), para los cuales el espesor de la subcapa viscoso y la altura de rugosidad son aproximadamente iguales), la rugosidad no tiene ningún efecto sobre el perfil de velocidad. Bajo estas condiciones, se encuentra que el perfil de velocidad sobre límites físicamente ásperos coincide con el de límites físicamente lisos, siempre que no coloquemos nuestro medidor de velocidad tan cerca del lecho que los elementos de rugosidad individuales distorsionen el campo de velocidad. La ley del muro para límites lisos, Ecuaciones\ ref {4.22} y\ ref {4.26} junto con la transición entre ellas a través de la capa de búfer, por lo tanto se mantiene para flujos con límites físicamente\(\rho u_{*} D / \mu<5\) más ásperos también. Estos son los flujos que en la sección sobre resistencia al flujo se denominaron dinámicamente suaves aunque físicamente rugosos y se demostró que caían en la curva para límites físicamente lisos en el diagrama de resistencia en la Figura 4.6.7. Para muy grandes\(\rho u_{*} D / \mu\), sin embargo, no hay subcapa viscosa y por lo tanto ningún efecto de\(\mu\) sobre el perfil de velocidad, y se debe esperar ver un perfil de velocidad que sea bastante diferente de la ley de la pared para un flujo suave. Las siguientes dos subsecciones están dedicadas al perfil de velocidad en estos flujos dinámicamente ásperos.

Figura\(\PageIndex{9}\): Diferentes regiones de flujo en función de la distancia desde el límite en flujo dinámicamente áspero.

Segundo, en el caso del flujo aproximado el valor de\(y\) relativo a\(D\) es importante (Figura\(\PageIndex{9}\)). Porque\(y \approx D\), en los puntos del flujo que se encuentran enclavados entre los propios elementos de rugosidad o están solo unas pocas alturas de rugosidad por encima de las partes superiores de los elementos de rugosidad, la velocidad depende de manera complicada de las formas de los elementos de rugosidad y de la posición del perfil en relación con el individuo elementos, y no debemos esperar encontrar ningún perfil de aplicación general; podría decirse que el perfil de velocidad está espacialmente desunificado. Un poco más alto en el flujo, varios diámetros por encima de las partes superiores de los elementos, las estelas desprendidas por elementos individuales se mezclan de tal manera que el perfil de velocidad es aproximadamente el mismo en todas las posiciones, pero la estructura del flujo aún se ve afectada por la turbulencia generada por la rugosidad. Muy por encima de las cimas de los elementos, sin embargo\(y>> D\), pues, es razonable esperar que la estructura de turbulencia esté gobernada por dinámicas locales, como en flujo suave, y no por las estelas de los pequeños elementos de rugosidad muy por debajo. Si\(D\) es suficientemente menor que la profundidad del flujo\(d\), entonces debería haber una capa del flujo para la cual\(y << d\) y\(y >> D\) al mismo tiempo, es decir, una parte de la capa interna en la que la turbulencia generada por la rugosidad no es de importancia directa. Recuerde, sin embargo, que por analogía con lo dicho sobre el flujo suave arriba, esta parte del perfil aún tiene que anclarse en su extremo inferior a esa parte del perfil de velocidad controlada por la turbulencia generada por la rugosidad generada.

A continuación presentaré el perfil de velocidad en flujos rugosos para los que efectivamente existe una zona para la cual\(y << d\) pero al mismo tiempo\(y >> D\) (o, más precisamente, por encima de la capa cercana al lecho de desunificación espacial del perfil, que es algo así como varias alturas de rugosidad por encima de las cimas de los elementos de rugosidad). Voy a tratar sólo con la región lo suficientemente lejos por encima de la cama como para que los elementos de rugosidad no afecten a la forma del perfil; esto podría llamarse “la capa interna muy por encima de los elementos de rugosidad”. Voy a hacer sólo unos breves comentarios sobre los flujos igualmente importantes en los que no hay zona para la cual\(y << d\) y\(y >> D\), ejemplos son flujos poco profundos en arroyos de lecho gravoso.

En la parte de la capa interna para la cual\(y >> D\),\(\mu\) ni\(D\) afecta la pendiente del perfil de velocidad. Por lo tanto, podemos hacer exactamente la misma afirmación que para la parte dominada por turbulencias de la capa interna en flujo físicamente suave: el gradiente de velocidad\(d \overline{u} /dy\) depende solo de\(\tau_{\text{o}}\),\(\rho\), y\(y\). Esto lleva de nuevo a la Ecuación\ ref {4.23}, y tras la integración, a la Ecuación\ ref {4.24}. Incluso debemos esperar que la constante\(A\) sea la misma, porque es una manifestación del transporte turbulento vertical del impulso fluido fluvial, y acabamos de concluir que suficientemente lejos del límite la estructura de la turbulencia depende solo de los efectos locales y es independiente de la turbulencia desprendida por la rugosidad límite. La constante de integración\(A_{1}\), sin embargo, es diferente, ya que depende de la naturaleza del perfil de velocidad de conexión más cercano al límite, que es diferente a la del flujo suave. Esta última diferencia tiene que ver con la importancia relativa del esfuerzo cortante viscoso y el esfuerzo de cizallamiento turbulento cerca del límite, y con la importancia relativa de la resistencia viscosa y la resistencia a la presión en el límite: si\(D>>\mu / \rho u_{*}\) (llamé tales flujos completamente rugosos), esfuerzo de cizallamiento viscoso en el flujo y viscoso arrastre en el límite son insignificantes, por lo que no solo el gradiente de velocidad sino también la velocidad en sí no se ve afectada por μ en la capa bajo consideración aquí.

Podemos reorganizar la Ecuación\ ref {4.24} para obtener la Ecuación\ ref {4.25} al igual que en el caso del flujo suave, pero con una diferencia importante: por comparación con la forma general de la ley de la pared para el flujo aproximado (Ecuación\ ref {4.29}), el término ahora no\(B\) es una constante sino una función de la número de Reynolds límite:

\[\frac{\overline{u}}{u_{ .}}=A \ln \frac{\rho u_{*} y}{\mu}+f\left(\frac{\rho u_{*} D}{\mu}\right) \label{4.30} \]

La ecuación\ ref {4.30} se puede poner en una forma equivalente pero más reveladora y más útil\(f\left(\rho u_{*} D / \mu\right)\) dividiéndose en dos partes:\(-A \ln \left(\rho u_{*} D / \mu\right)\) más un resto que es alguna función diferente de\(\rho u_{*} D / \mu\), que voy a llamar\(B^{\prime}\). La única razón para esta elección por lo demás arbitraria es que ahora la Ecuación\ ref {4.30} se puede escribir

\(\frac{\overline{u}}{u_{*}}=A\left(\ln \frac{\rho u_{* }y}{\mu}-\ln \frac{\rho u_{*} D}{\mu}\right)+\mathrm{B}^{\prime}\)

\[=A \ln \frac{y}{D}+B^{\prime} \label{4.31} \]

La ecuación\ ref {4.31} es más ordenada que la ecuación\ ref {4.30}, pero recuerda que\(B^{\prime}\) es una función de\(\rho u_{*} D / \mu\). Si\(\rho u_{*} D / \mu\) es suficientemente grande, sin embargo, para que\(D\) sea grande en relación con lo que sería el grosor de la subcapa de viscosidad, la turbulencia se extiende hacia abajo entre los elementos de rugosidad y no hay una capa dominada por la viscosidad junto al fondo. El perfil de velocidad entonces no puede depender\(\mu\) y por lo tanto no de\(\rho u_{*} D / \mu\), por lo que\(B^{\prime}\) en la Ecuación\ ref {4.31} es una constante, que tiene un valor de aproximadamente\(8.5\) para rugosidad de grano de arena uniforme y apretada. (Hay tanta incertidumbre sobre esta constante como sobre la constante\(B\) en la Ecuación\ ref {4.25}.) De hecho, se\(B\) ha encontrado experimentalmente que el valor de se vuelve constante para\(\rho u_{*} D / \mu > 60\). Es bajo estas condiciones que el flujo se denominó completamente rugoso en la sección anterior sobre resistencia al flujo. La ecuación\ ref {4.31} se puede escribir entonces como Ecuación\ ref {4.32}, la ley de la pared para un flujo completamente rugoso:

\[\frac{\overline{u}}{u_{*}}=2.5 \ln \frac{y}{D}+8.5 \label{4.32}\]

La figura\(\PageIndex{10}\) muestra la Ecuación\ ref {4.32} junto con los datos de Nikuradse (1933) sobre los que originalmente se\(B^{\prime}\) derivó el valor de\(8.5\) for. Los datos de Nikuradse se obtuvieron para una geometría particular de rugosidad granular fabricada pegando una monocapa algo abierta de arena subredondeada y casi de un solo tamaño a las paredes internas de tuberías circulares. Se debe esperar que el valor de\(B^{\prime}\) sea diferente para diferentes geometrías de rugosidad, incluso si la altura promedio de rugosidad es la misma, porque la forma y disposición de los elementos de rugosidad serían diferentes, y esto afecta los detalles de la estructura de turbulencia justo cerca del límite y así también el perfil de velocidad justo cerca del límite.

Figura\(\PageIndex{10}\): Gráfica de\(\overline{u} / u^{*}\) vs.\(y/D\) para la capa interna sobre límites granular-rugosos. Los datos son de Nikuradse (1933) para corridas con radio de tubería\(> 60D\). Sólo se muestran datos para\(\text{Re}^{*} > 60\) los que se muestran, por lo que esta gráfica representa la ley del muro para un flujo dinámicamente completamente rugoso. Se muestran todos los puntos hasta\(0.2\) veces el radio de la tubería. Se incluyen ocho perfiles de cuatro tuberías revestidas de arena. Como se describe en una sección posterior, el\(y = 0\) nivel se ha ajustado hacia abajo desde la parte superior de los granos una distancia\(y/D = -0.36\) para extender el ajuste en línea recta lo más cerca posible del lecho.

La figura\(\PageIndex{11}\) es otra gráfica de la Ecuación\ ref {4.32}, esta vez sin los puntos de datos. Está destinado a servir como una advertencia sobre qué tan cerca del límite se aplica realmente la Ecuación\ ref {4.32}. Recordemos que en alturas no mayores a unos pocos tamaños de elementos de rugosidad, se puede decir que el flujo está desunificado espacialmente (véase el párrafo 114 anterior), y en esa región ya no se sostiene la base para la derivación de la Ecuación\ ref {4.32}. Eso se enfatiza, en forma de caricatura, por el desenfoque del perfil cerca del límite áspero.

Figura\(\PageIndex{11}\): Gráfica de\(\overline{u} / u^{*}\) vs\(y/D\) para la capa interna sobre límites granular-rugosos (Ecuación\ ref {4.32}), mostrando la región cerca del lecho donde el perfil no sigue la Ecuación\ ref {4.32}.

Como se hace comúnmente, puede conservar el valor de\(8.5\) for\(B^{\prime}\) en la Ecuación\ ref {4.31} y usarlo para\(D\) el diámetro ficticio de granos de arena de un solo tamaño en una monocapa uniforme que haga que la Ecuación\ ref {4.31} se ajuste mejor a los datos de velocidad. A ese tamaño se le llama la rugosidad equivalente de la arena, generalmente denotada\(k_{s}\). (Un término más descriptivo sería la “rugosidad de arena equivalente al estilo Nikuradse”). En otras palabras,\(k_{s}\) para cualquier rugosidad de lecho dada, de cualquier tipo, es la altura uniforme de grano de arena que da la misma distribución de velocidad de ley de pared para un valor dado de\(\tau_{\text{o}}\). A la vista esto parece una forma ordenada alrededor del problema de cuál\(B^{\prime}\) es el valor de, pero ten en cuenta que para determinar\(B^{\prime}\) en primer lugar se necesita medir tanto el perfil de velocidad como el esfuerzo cortante límite, independientemente, al mismo tiempo.

Para\(5<\rho u_{*} D / \mu<60\) el flujo se dice que es transicionalmente áspero. El perfil de velocidad sigue siendo una línea recta semilogada para\(y >> D\), ya\(\overline{u} /u_{*}\) sea trazada contra\(\rho u_{*} y / \mu\) como en la Figura\(\PageIndex{6}\) o contra\(y/D\) como en Figura\(\PageIndex{10}\), y sigue teniendo la misma pendiente dada por la constante universal\(A\). Pero la posición de la línea recta varía a medida que la parte cercana al lecho del perfil cambia del perfil de flujo suave mostrado en la Figura\(\PageIndex{6}\) al perfil completamente rugoso que se muestra en la Figura\(\PageIndex{10}\). Para los flujos transicionalmente ásperos, la ley del muro en la región más interna, donde hay cierta dependencia\(\mu\), no puede derivarse en forma de una ecuación simple como la Ecuación\ ref {4.26} o la Ecuación {4.31}; tenga en cuenta, sin embargo, que alguna forma de la ley general del muro para límites rugosos ( Ecuación\ ref {4.30}) se mantiene ahí sin embargo.

Finalmente, si\(\rho u_{*} D / \mu\) es muy pequeño los elementos de rugosidad están profundamente incrustados en la subcapa viscosa y no pueden tener ningún efecto sobre la estructura de la turbulencia y la forma del perfil de velocidad por encima de la subcapa viscosa. El perfil de velocidad es entonces el mismo que si el límite fuera físicamente suave. Como se discutió anteriormente en la sección sobre resistencia al flujo, el flujo es dinámicamente suave aunque físicamente áspero.

Figura\(\PageIndex{12}\): Gráficas combinadas de la ley del muro en flujos lisos, transicionalmente rugosos y completamente rugosos.

Figura\(\PageIndex{13}\): Rangos de rugosidad Número de Reynolds para flujos dinámicamente suaves, flujos transicionalmente rugosos y flujos completamente rugosos.

Figura\(\PageIndex{12}\), una gráfica combinada de la ley del muro en flujos lisos y rugosos, resume gran parte de lo que hay en esta sección y la anterior (ver también Figura\(\PageIndex{13}\)). La superficie tridimensional en la Figura\(\PageIndex{12}\), dibujada mediante el uso de las Ecuaciones\ ref {4.22},\ ref {4.26}, y\ ref {4.32},\(\overline{u} /u_{*}\) se muestra como una función de\(y^(+)\) y\(\text{Re}_{*}\). En flujos lisos, representados por la parte izquierda de la superficie, los perfiles de velocidad no dependen de ellos\(\text{Re}_{*}\), por lo que la superficie es un cilindro cuyos elementos son paralelos al\(\text{Re}_{*}\) eje. Cada uno de los diversos perfiles mostrados, que representan intersecciones de la superficie con planos para los cuales\(\text{Re}_{*} = const\), es exactamente el mismo que el de la Figura\(\PageIndex{6}\). En flujos completamente rugosos, representados por la región a la derecha del plano\(\text{Re}_{*} = 60\), los perfiles de velocidad dependen únicamente de\(y/D\). Para ver por qué la parte derecha de la superficie se inclina hacia abajo hacia la derecha, escriba\(\ln (y / D)\) como\(\ln \left(\rho u_{*} y / \mu\right)-\ln \left(\rho u_{*} D / \mu\right)\), o\(\ln y^{+}-\ln \mathrm{Re}_{*}\); así, cuanto mayor sea el valor de\(\text{Re}^{*}\), menor será el valor de\(\overline{u} / u_{*}\) para un valor dado de\(y^{+}\). Debido a que no hay una subcapa viscosa o capa amortiguadora con la que lidiar, los perfiles son líneas rectas hasta posiciones no muy por encima de las partes superiores de los elementos de rugosidad. El perfil de pared rugosa se desvía de una línea recta semilogada dentro de varias alturas de rugosidad por encima de las partes superiores de los elementos de rugosidad, por no hablar de la desunificación espacial del perfil de velocidad que se establece en un nivel justo por encima de las partes superiores de los elementos de rugosidad. Sólo en puntos de la superficie de la Figura\(\PageIndex{12}\) muy por encima de la curva discontinua que expresa la condición\(y = D\) son válidos los perfiles; la parte de la superficie que se muestra en la parte inferior derecha es, por lo tanto, útil solo hipotéticamente, para mostrar la naturaleza de las relaciones. Finalmente, en la parte media de la superficie los perfiles son transicionales entre los perfiles lisos y los completamente rugosos. Aquí las líneas para\(y^{+} = 5\) y\(y^{+} = 30\) mostradas en la parte izquierda de la superficie pierden su significado físico a medida que desaparece la subcapa viscosa.

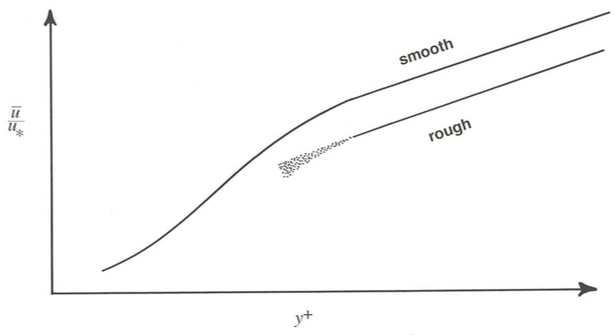
\(\PageIndex{12}\)Obsérvese en Figura que a cualquier valor de\(y^{+}\) pozo arriba\(\overline{u} /u_{*}\) en la capa interna en cualquier flujo rugoso es menor que\(\overline{u} /u_{*}\) en cualquier flujo suave, aunque las pendientes de los perfiles para los dos flujos son las mismas a esa altura. Esto se debe a que más cerca del fondo la velocidad aumenta más bruscamente con la distancia desde el fondo en flujo suave que en flujo áspero. La figura\(\PageIndex{14}\) muestra ese efecto, en forma de caricatura: el perfil para flujo áspero se encuentra por todas partes debajo del perfil para un flujo suave. Se puede pensar en los dos perfiles mostrados en la Figura\(\PageIndex{14}\) como representativos de los extremos izquierdo y derecho de la superficie mostrada en la Figura\(\PageIndex{12}\), dado que la superficie se inclina hacia abajo hacia la derecha en la Figura\(\PageIndex{12}\).

Figura\(\PageIndex{14}\): Gráfica de dibujos animados que muestra la comparación entre perfiles de velocidad para flujo suave y flujo rugoso.

Un paso adicional convencional que se toma con la Ecuación\ ref {4.31} es escribir\(B^{\prime}\) en la forma\(-A \ln \left(y_{0} / D\right)\), donde la cantidad\(y_{\text{o}}\), con las dimensiones de longitud, se denomina longitud de rugosidad. (Al aire libre, los dinamistas de fluidos como los meteorólogos toman la dirección de coordenadas de normal a límite para ser\(z\), por lo que tratan\(z_{\text{o}}\), no)\(y_{\text{o}}\). Nota: si lee la literatura sobre perfiles de velocidad en entornos de flujo natural, es probable que encuentre esta longitud de rugosidad, en lugar de las cantidades equivalentes que he usado anteriormente en esta sección.

El uso de\(y_{\text{o}}\)\(B^{\prime}\) permite ser completamente absorbido en el término logarítmico en la Ecuación\ ref {4.32}:

\(\frac{\overline{u}}{u_{*}}=A \ln \frac{y}{D}-A \ln \frac{y_{o}}{D}\)

\[=A \ln \frac{y}{y_{o}} \label{4.33} \]

Por la definición del logaritmo natural, se\(y_{\text{o}}\) puede escribir en términos de\(B^{\prime}\) como\(y_{0}=D \exp \left(-B^{\prime} / A\right)\).

Si el flujo es sólo transicionalmente áspero,\(y_{\text{o}}\) es una función de\(\rho u_{*} D / \mu\), como es\(B^{\prime}\). Si el flujo es completamente rugoso, sin embargo,\(y_{\text{o}}\) es independiente de\(\rho u_{*} D / \mu\) por la misma razón que\(B^{\prime}\) en la Ecuación\ ref {4.30} es independiente de\(\rho u_{*} D / \mu\).

Nota

Advertencia: no confundir\(y_{\text{o}}\) con la altura de rugosidad real\(D\): para una geometría dada de rugosidad en flujo completamente rugoso\(y_{\text{o}}\) es proporcional a\(D\) (para rugosidad uniforme de grano de arena compacta\(y_{0}=D / 30\)), pero el coeficiente de proporcionalidad varía considerablemente dependiendo de geometría particular de la rugosidad.

Ajuste\(y\) igual a\(y_{\text{o}}\) en Ecuación\ ref {4.33} da\(\overline{u} / u_{*}=0\). Entonces otra forma de ver\(y_{\text{o}}\) es que es la altura a la que la velocidad se convertiría en cero si la ecuación logarítmica de pared rugosa para el perfil de velocidad pudiera extenderse hasta esa altura. Es importante recordar, sin embargo, que la Ecuación\ ref {4.33} se vuelve inaplicable muy por encima de esa posición, que se encuentra enclavada entre los elementos de rugosidad. (Por eso utilicé la construcción del verbo “subjuntivo” contrario a hecho en la oración anterior.) Ver los comentarios muy breves en el siguiente párrafo.

Todavía no hemos considerado la parte más baja de la capa interna, no muy por encima de las partes superiores de los elementos de rugosidad. Para la rugosidad del lecho del tamaño de la arena esta región no es mucho más de unos pocos milímetros de espesor, pero para el agua que fluye sobre gravas o para el viento que sopla sobre grandes rugosidad de la superficie del suelo como edificios o vegetación puede ser decímetros o incluso metros de espesor, y no se necesitan medidores de velocidad sofisticados y miniaturizados para incluirlo en perfiles de velocidad medidos. En posiciones tan cercanas a la cama, surgen dos complicaciones: el perfil logarítmico se distorsiona, y no hay opción obvia para\(y = 0\).

Ley de Defecto de Velocidad

Ahora mira el perfil de velocidad en la capa exterior. Allí la velocidad se especifica de manera más natural en relación con la del límite con el flujo libre (o, en el caso del flujo de superficie libre, relativa a la velocidad superficial, o en el caso del flujo de tubería, relativo a la velocidad de la línea central), porque hemos visto que la capa interna, con una relación diferente para la velocidad, interviene entre la capa externa y el límite inferior. En otras palabras, si miramos la velocidad relativa a esa en la superficie no tenemos que preocuparnos de cómo se ancla la velocidad al fondo a través de la capa interna. Entonces en lugar de\(\overline{u}\) usar\(U_{s}-\overline{u}\), llamado defecto de velocidad, donde\(U_{s}\) está la velocidad de la superficie (es decir, máxima).

Si regresas y revisas la discusión en la sección sobre capas internas y externas verás que la estructura de la turbulencia en la capa externa debe depender de\(\tau_{\text{o}}\),,\(\rho\), y\(y\)\(d\), pero no de\(\mu\), por la misma razón que el perfil de velocidad en la turbulencia- parte dominada de la capa interna no depende de\(\mu\). Debido a que esto es cierto desde la superficie libre hasta la parte inferior de la capa externa, y porque\(U_{s}-\overline{u}\) caracteriza la velocidad relativa a la superficie libre en lugar de la parte inferior, entonces no solo el gradiente de velocidad\(d\overline{u} /dy\) (como en la parte turbulenta de la capa interna) sino también en\(U_{s}-\overline{u}\) sí mismo es independiente de\(\mu\). La turbulencia estructura y no\(U_{s}-\overline{u}\) debe depender de\(D\) ninguno de los dos, siempre y cuando eso\(D << d\). Entonces la forma general del perfil de velocidad-defecto es

\[U_{s}-\overline{u}=f\left(\tau_{o}, \rho, y, d\right) \label{4.34} \]

o en forma adimensional

\[\frac{U_{s}-\overline{u}}{u_{*}}=f\left(\frac{y}{d}\right) \label{4.35} \]

La ecuación\ ref {4.35} nos dice que el defecto de velocidad adimensional depende únicamente de la altura adimensional por encima de la parte inferior. Esta relación para el perfil de velocidad en la capa externa se llama la ley velocidad-defecto. Aplazaré la discusión adicional sobre los perfiles de velocidad en la parte exterior del flujo hasta la siguiente sección, donde un examen de la región de superposición entre las capas interna y externa permite una mayor comprensión de la forma de la ley de velocidad-defecto.

La capa de superposición; más sobre la ley de velocidad-defecto

Un asunto más a considerar en esta exposición de perfiles de velocidad tiene que ver con la capa de superposición, donde a un flujo medio suficientemente alto Reynolds numera las condiciones que definen las capas interna y externa se mantienen simultáneamente; les remito una vez más a la sección anterior sobre capas internas y externas. Esta capa de superposición está lo suficientemente lejos del fondo como para que la estructura de flujo sea independiente tanto de la viscosidad como de las características de la rugosidad del fondo pero lo suficientemente cerca del fondo como para que la estructura de flujo sea independiente de la profundidad de flujo (Figura\(\PageIndex{15}\)). Aquí los perfiles de velocidad de capa interna y capa externa deben coincidir, es decir, las velocidades dadas por la ley de la pared y por la ley de velocidad-defecto en cualquier nivel en la capa de superposición deben ser las mismas. El límite superior de la capa de superposición está en la parte superior de la capa interna. En flujo suave el límite inferior está en la parte superior de la capa tampón. Con respecto al límite inferior en flujo rugoso, presumiblemente la representación velocidad-defecto del perfil de velocidad, que mira hacia abajo desde la superficie libre y puede ignorar los detalles de la rugosidad del fondo, debe comenzar a descomponerse cuando llegue a la parte inferior de la capa interna, donde se ha visto que la rugosidad hace que el perfil de la capa interna se curve lejos de una línea recta semilogada.

Figura\(\PageIndex{15}\): La capa de superposición (la capa logarítmica) para ley de pared lisa, ley de pared rugosa y ley de defecto de velocidad.

Las restricciones impuestas por el requisito de coincidencia en la forma tanto de la ley de muro como de la ley de velocidad-defecto en la capa de superposición fueron percibidas por primera vez por Izakson (1937) y Millikan (1939). La consecuencia matemática de este emparejamiento, que no voy a detallar aquí, es que en la capa de superposición —pero no más lejos, más allá de la capa interna— la ley de defectos de velocidad, así como la ley de muro, es de forma logarítmica. La capa de superposición suele llamarse capa logarítmica, porque en ella tanto la ley de muro como la ley de defectos son logarítmicas.

Figura\(\PageIndex{16}\): Perfiles de velocidad-defecto: gráficas de flujos\((U_{s} - \overline{u} )/u_{*}\) versus\(y/D\) en capa límite con cuatro geometrías: A) placa plana; B) tubo circular; C) conducto plano ancho; y D) flujo de canal abierto. Después de Monin y Yaglom (1971) (diversas fuentes), y Coleman (1981). Las líneas rectas con pendientes de\(-A (= -1/\kappa)\) se ajustan a puntos para\(y/d < 0.2\).

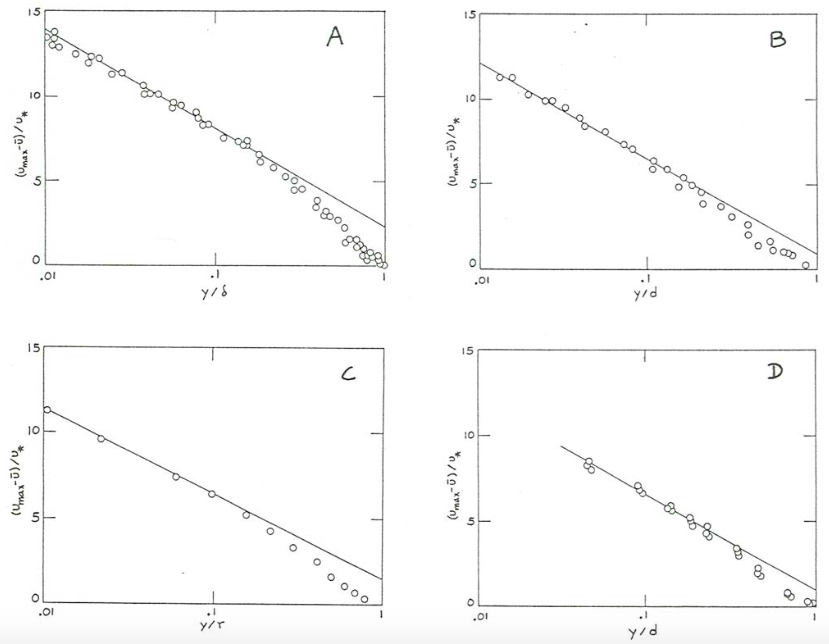
La figura\(\PageIndex{16}\) muestra perfiles de velocidad-defecto en placas planas y en tuberías, conductos planos anchos y canales abiertos. Los datos de canal abierto, de Coleman (1981), son para una relación ancho-profundidad de solo aproximadamente\(2\), pero no he podido encontrar ningún dato mejor; la escasez de buenos datos publicados sobre perfiles de velocidad completos de superficie a fondo en flujos de canal abierto uniformes y constantes en grandes proporciones de ancho a profundidad es llamativo. En cada gráfica de\(\PageIndex{16}\) la Figura los puntos de datos definen una sola curva que mantiene para un amplio rango de números de Reynolds de flujo medio, lo que indica que nuestras suposiciones sobre los controles de velocidad y turbulencia en la capa externa están justificadas. En cada gráfica hay un segmento semilog de línea recta bien definido para bastante pequeño\(y/d\); esa es la capa logarítmica. Hacia la posición de velocidad máxima en\(y/d = 1\) el perfil se separa de la línea recta semilog para alcanzar el punto\((U_{s} - \overline{u} )/u_{*} = 0\) en la posición de velocidad máxima.

La forma diferente de la parte exterior del perfil de velocidad-defecto en diferentes geometrías de flujo es de esperar debido a diferentes efectos físicos en el movimiento y geometría de grandes remolinos en la región del flujo más alejada del límite sólido. Debido a que el borde exterior de una capa límite turbulenta de crecimiento libre es de forma altamente irregular (Capítulo 3), en cualquier punto cerca del borde exterior, el paso de grandes remolinos turbulentos se alterna con el paso de fluido no turbulento, por lo que la eficacia del intercambio de momento turbulento es menor y la velocidad gradiente correspondientemente más empinado que en las regiones más cercanas al límite; esto explica la gran divergencia del perfil desde el segmento semilogo de línea recta en la Figura\ (\ PageIndex {16}\ A. En tuberías y conductos planos, la divergencia similar pero menor podría explicarse por el paso libre de grandes remolinos a través la línea central o el plano central desde los lados opuestos del flujo. En el flujo de canal abierto, un efecto similar podría ser producido por el aplanamiento de remolinos grandes que se mueven hacia la superficie libre. Los escasos datos de los canales abiertos sugieren un efecto similar en magnitud al de tuberías y conductos planos, o quizás incluso más pequeño. Parece que no hay razón para esperar un perfil perfectamente logarítmico hasta la superficie libre, pero las desviaciones claramente son insustanciales, al menos para el trabajo práctico.

Efectos de la Rugosidad Altura y Espaciado

De alguna manera es desalentador sentarse y considerar que casi todo lo dicho hasta ahora sobre los perfiles de velocidad se limita al caso del flujo libre de sedimentos sobre elementos de rugosidad apretados cuyo tamaño es una pequeña fracción de la profundidad del flujo. Obviamente, esto es solo un pequeño subconjunto de flujos turbulentos de capa límite sobre límites ásperos. La discusión en esta sección enfatiza principalmente los efectos cualitativos que se esperan como

1. La altura de los elementos de rugosidad aumenta en relación con la profundidad de flujo.
2. El espaciamiento de los elementos de rugosidad aumenta con respecto a su altura.

La figura\(\PageIndex{17}\) resume los cambios en el perfil de velocidad a medida que el tamaño de la rugosidad granular compacta aumenta en relación con la profundidad de flujo. En la Figura\(\PageIndex{17}\) A las partículas son tan pequeñas (o, más precisamente, el número de rugosidad de Reynolds\(\rho u_{*} D / \mu\) es tan pequeño) que las partículas están incrustadas en una subcapa viscosa, y el flujo es dinámicamente suave. En la Figura\(\PageIndex{17}\) B las partículas son más grandes y el flujo es dinámicamente rugoso, pero el tamaño de partícula sigue siendo tan pequeño en relación con la profundidad de flujo que hay una capa externa bien desarrollada más allá de la capa de superposición en la que se mantiene el perfil de velocidad-defecto pero el perfil de capa interna no. Estos dos primeros casos están cubiertos por el tratamiento detallado anterior de los perfiles de velocidad.

Figura\(\PageIndex{17}\): Cambios en el perfil de velocidad a medida que el tamaño de la rugosidad granular compacta aumenta en relación con la profundidad de flujo.

En la Figura\(\PageIndex{17}\) C, a medida que la relación de profundidad de flujo a tamaño de partícula disminuye aún más, la distinción entre capas interna y externa comienza a ser borrosa, y eventualmente se alcanza una situación en la que todo el perfil, desde el fondo hasta la superficie libre, se ve afectado por los detalles de la rugosidad. Todo el perfil entonces se parece solo a la parte inferior del perfil de ley de pared en flujos con valores muy grandes de\(d/D\). Este efecto comienza a hacerse apreciable a\(d/D\) valores de algo así como\(10\) a\(15\).

A medida que\(d/D\) disminuye aún más, una fracción cada vez más grande de la profundidad de flujo total es ocupada por la zona del flujo, dentro de uno o quizás dos diámetros de grano por encima de las partes superiores de las partículas de rugosidad, donde el perfil de velocidad está espacialmente desunificado, en el sentido de que varía con la posición relativa a la disposición de las partículas. Como se muestra en la Figura\(\PageIndex{17}\) D en forma exagerada, para\(d/D\) valores por debajo de aproximadamente\(2\) o la\(3\) mayor parte o la totalidad del perfil de velocidad es espacialmente variable de esta manera.

Lo que sucede a medida que\(d/D\) disminuye aún más (Figura\(\PageIndex{17}\) E) depende del valor del número de Froude de flujo medio\(U/(gD)^{1/2}\). (Para una plena apreciación de este punto habrá que esperar hasta que haya presentado más sobre el flujo de superficie libre más adelante, en el siguiente capítulo.) Para números de Froude cercanos o mayores a uno (es decir, para flujo supercrítico o casi supercrítico), la superficie libre se deforma fuertemente por la presencia de las partículas justo debajo de la superficie; piense en un arroyo montañoso poco profundo de flujo rápido con un lecho de adoquines y cantos rodados. Sin embargo, para los mismos números muy pequeños\(d/D\) pero bajos de Froude, los granos descansan justo debajo de una superficie de agua relativamente plácida, o en el caso extremo se proyectan por encima de la superficie como islas.

La figura\(\PageIndex{18}\) es una caricatura que muestra los cambios en la estructura del flujo a medida que disminuye el espaciamiento de rugosidad en relación con la altura de rugosidad. Comience con un fondo físicamente liso y plano; el flujo es dinámicamente suave y\(y = 0\) se toma naturalmente en el fondo plano. Ahora toma un conjunto de elementos de rugosidad cuyas alturas son una fracción muy pequeña de la profundidad de flujo y comienzan a colocarlos ya sea al azar o en un patrón regular sobre la cama. Los elementos podrían ser cuerpos de farol tridimensionales o crestas bidimensionales transversales al flujo; los efectos son cualitativamente los mismos, al menos hasta que la relación de espaciamiento a altura se vuelve muy pequeña.

Figura\(\PageIndex{18}\): Cambios en la estructura de flujo a medida que disminuye el espaciamiento de rugosidad en relación con la altura de

Siempre que el número de rugosidad de Reynolds (basado en la altura de los elementos de rugosidad que se agregan) sea suficientemente grande, cada elemento crea una estela a medida que el flujo se separa a su alrededor. De la discusión sobre la separación de flujo en el Capítulo 3 se puede ver que la estructura de flujo aguas abajo de cada elemento de rugosidad es muy complicada: la capa límite de flujo suave se modifica profundamente por el desarrollo de una capa de cizallamiento altamente turbulenta que se extiende aguas abajo de la separación punto. Aguas abajo de cada elemento el flujo se reajusta gradualmente hacia la estructura de capas límite que existiría en ausencia de rugosidad; se dice que las estelas arrojadas por los elementos se relajan. Este reajuste o relajación toma la forma de una nueva capa más baja del flujo, expandiéndose hacia arriba a expensas de la capa de cizallamiento turbulento, en la que se establece un perfil de ley de pared dominado por turbulencias de la misma manera que en una capa límite que crece sobre una placa plana. Se necesita un número sorprendentemente grande de alturas de elementos aguas abajo, algo del orden de cien, para que se complete el proceso, después de lo cual la estructura local del flujo no muestra rastro de la presencia del elemento de rugosidad aguas arriba y la capa de ley de pared se extiende sin interrupción desde el plano abajo hacia arriba en la región del flujo muy por encima del nivel de las partes superiores de los elementos de gran rugosidad. El caso de los números de Reynolds de baja rugosidad es de menor interés aquí, porque entonces los elementos se incrustan en una subcapa viscosa, pero en ese caso también se crea un déficit en el momento del fluido aguas abajo de cada elemento a pesar de que el flujo no se separa, y este déficit se plancha aguas abajo por viscoso cizallamiento hasta que se restaure el perfil de velocidad dominada por viscosidad original.

Si los elementos de rugosidad están suficientemente separados (Figura\(\PageIndex{18}\) A) cada uno tiene una estela larga que se extiende aguas abajo, pero el flujo es capaz de volver a la normalidad antes de que encuentre el siguiente elemento de rugosidad. A esto se le ha denominado flujo de rugosidad aislada (Morris, 1955). El perfil de velocidad medido por encima de un punto dado en el lecho depende de la posición de ese punto en relación con las estelas detrás de los elementos. Tendrías que medir una gran cantidad de perfiles y promediarlos espacialmente para obtener un perfil que represente todo el flujo. Comparado con el perfil original de flujo suave antes del emplazamiento de cualquier elemento de rugosidad, el perfil promediado espacialmente muestra un déficit de velocidad dentro de una o dos alturas de rugosidad del lecho.

El esfuerzo cortante límite promediado espacialmente\(\tau_{\text{o}}\) es todavía predominantemente viscoso, como en ausencia de elementos de rugosidad, pero la contribución de la resistencia a la presión\(\tau_{\text{o}}\) aumenta con la densidad de rugosidad. El flujo ahora podría denominarse transicionalmente rugoso, aunque en un sentido bastante diferente del uso de ese término en flujo sobre rugosidad apretada en secciones anteriores. Obsérvese también que el flujo original, antes del emplazamiento de los elementos de rugosidad, puede ser por sí mismo dinámicamente rugoso, si el fondo está cubierto con rugosidad apretada que es mucho menor que la rugosidad grande y aislada que estamos agregando. Entonces τo está dominado desde el principio por la resistencia a presión, pero esta resistencia a la presión es de dos partes: una parte espacialmente uniforme producida por la rugosidad subyacente pequeña y apretada, y una parte espacialmente no uniforme producida por la rugosidad grande y aislada. Solo se necesita una baja densidad de elementos de gran rugosidad para que su contribución a la resistencia a la presión supere a la de los elementos empaquetados.

A medida que continuamos agregando grandes elementos de rugosidad, se alcanza un punto donde las estelas arrojadas por los elementos no se relajan completamente antes de encontrarse con otro elemento de rugosidad aguas abajo, y con algún aumento adicional en la densidad, la mayoría de los puntos en el flujo cercano al lecho se encuentran dentro de las estelas en diversas etapas de relajación ( Figura\(\PageIndex{18}\) B). Ahora no hay lugar en el lecho que muestre el perfil de velocidad relativamente simple del flujo suave original sin elementos de rugosidad. Un flujo de este tipo se ha llamado flujo de interferencia de vigilia (Morris, 1955). Nuevamente hay que tomar una gran cantidad de perfiles de velocidad locales y promediarlos espacialmente para obtener un perfil representativo de toda la cama. Debido a que la mayor parte del área del lecho está superpuesta por despertadores reunidos y relajantes, el perfil promediado espacialmente muestra dos segmentos distintos: uno, adyacente al lecho y que se extiende hacia arriba por alguna fracción de la altura de rugosidad, representa el promedio espacial de los perfiles locales de ley de pared en las estelas relajantes , y la otra, comenzando muy por encima de las partes superiores de los grandes elementos de rugosidad y extendiéndose muy por encima, representa la ley del muro por encima de la zona en la que la turbulencia de estela que se difunde hacia arriba se funde en una capa espacialmente uniforme, el caso que se trató extensamente en la parte anterior de este capítulo. Estas dos partes distintivas del perfil tienden a trazar como líneas rectas semilogadas con una transición a alturas algo por debajo a algo por encima de las partes superiores de los elementos de rugosidad. Véase Nowell and Church (1979) para un buen ejemplo. A medida que disminuye el espaciado de rugosidad, la altura del\(y = 0\) nivel para el perfil general de ley de pared por encima de las partes superiores de los elementos de rugosidad se eleva cada vez más por encima del fondo plano.

Con el aumento de la densidad de rugosidad, eventualmente la mayor parte del área del lecho entre los elementos de rugosidad se superpone por las partes de las estelas que se encuentran aguas arriba en lugar de aguas abajo del reacoplamiento (Figuras\(\PageIndex{18}\) C,\(\PageIndex{18}\) D); esta condición se establece cuando la relación entre el espaciamiento de la rugosidad y la altura de rugosidad es del orden de diez o menos. Mucho antes de esta etapa el segmento de línea recta inferior del perfil de velocidad promediado espacialmente pierde su carácter distintivo. Las capas de cizallamiento turbulentas aguas abajo de los lugares de separación chocan principalmente sobre las superficies de los elementos de rugosidad aguas abajo en lugar de sobre el fondo plano; las tensiones de cizallamiento viscosas en el fondo plano son casi inexistentes, y la geometría del fondo en las áreas entre los elementos de rugosidad es irrelevante a la dinámica del flujo. Para la rugosidad granular tridimensional, esta condición se mantiene sin ningún cambio cualitativo a medida que los elementos se espacian tan estrechamente que sus bases se tocan, una buena aproximación a la condición de un lecho granular suelto tratado en detalle anteriormente. Sin embargo, si la rugosidad consiste en crestas transversales, la relación de espaciamiento a altura puede continuar disminuyendo hacia cero, y a medida que se vuelve más pequeña que aproximadamente una, el flujo pasa por las crestas de las crestas e impulsa una circulación de vórtices estables ubicados en los canales profundos y estrechos entre los crestas; esto se ha llamado flujo de desnatado (Morris, 1955).