8.9: Derivabilidad y consistencia

Última actualización
Guardar como PDF

Page ID: 103665

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Template:MathJaxZach

Ahora estableceremos una serie de propiedades de la relación de derivabilidad. Son independientemente interesantes, pero cada uno jugará un papel en la prueba del teorema de integridad.

Proposición\(\PageIndex{1}\)

Si\(\Gamma \Proves A\) y\(\Gamma \cup \{A\}\) es inconsistente, entonces\(\Gamma\) es inconsistente.

Prueba. Hay finitos\(\Gamma_0\) y\(\Gamma_1 \subseteq \Gamma\) tales que\(\Log{LK}\) deriva\(\Gamma_0 \Sequent A\) y\(A, \Gamma_1 \Sequent \quad\). Que la\(\Log{LK}\) -derivación de\(\Gamma_0 \Sequent A\) ser\(\pi_0\) y la\(\Log{LK}\) -derivación de\(\Gamma_1, A \Sequent \quad\) ser\(\pi_1\). Entonces podemos derivar

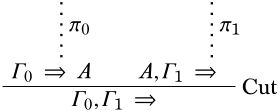
8.9.1.png

Desde\(\Gamma_0 \subseteq \Gamma\) y\(\Gamma_1 \subseteq \Gamma\),\(\Gamma_0 \cup \Gamma_1 \subseteq \Gamma\), por lo tanto\(\Gamma\) es inconsistente. ◻

Proposición\(\PageIndex{2}\)

\(\Gamma \Proves A\)iff\(\Gamma \cup \{\lnot A\}\) es inconsistente.

Prueba. Primero supongamos\(\Gamma \Proves A\), es decir, hay una derivación\(\pi_0\) de\(\Gamma \Sequent A\). Al agregar una\(\LeftR{\lnot}\) regla, obtenemos una derivación de\(\lnot A, \Gamma \Sequent \quad\), es decir,\(\Gamma \cup \{\lnot A\}\) es inconsistente.

Si\(\Gamma \cup \{\lnot A\}\) es inconsistente, hay una derivación\(\pi_1\) de\(\lnot A, \Gamma \Sequent \quad\). La siguiente es una derivación de\(\Gamma \Sequent A\):

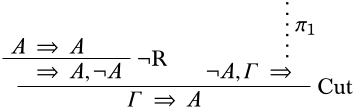
8.9.2.png

◻

Problema\(\PageIndex{1}\)

Demostrar que\(\Gamma \Proves \lnot A\) iff\(\Gamma \cup \{A\}\) es inconsistente.

Proposición\(\PageIndex{3}\)

Si\(\Gamma \Proves A\) y\(\lnot A \in \Gamma\), entonces\(\Gamma\) es inconsistente.

Prueba. Supongamos\(\Gamma \Proves A\) y\(\lnot A \in \Gamma\). Después hay una derivación\(\pi\) de un secuente\(\Gamma_0 \Sequent A\). El secuente también\(\lnot A, \Gamma_0 \Sequent \quad\) es derivable:

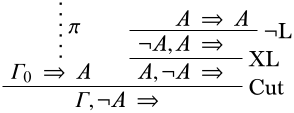
8.9.3.png

Desde\(\lnot A \in \Gamma\) y\(\Gamma_0 \subseteq \Gamma\), esto demuestra que\(\Gamma\) es inconsistente. ◻

Proposición\(\PageIndex{4}\)

Si\(\Gamma \cup \{A\}\) y ambos\(\Gamma \cup \{\lnot A\}\) son inconsistentes, entonces\(\Gamma\) es inconsistente.

Prueba. Hay conjuntos finitos\(\Gamma_0 \subseteq \Gamma\) y\(\Gamma_1 \subseteq \Gamma\) y\(\Log{LK}\) -derivaciones\(\pi_0\) y\(\pi_1\) de\(A, \Gamma_0 \Sequent \quad\) y\(\lnot A, \Gamma_1 \Sequent \quad\), respectivamente. Entonces podemos derivar

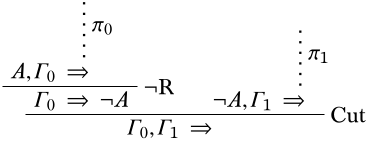
8.9.4.png

Desde\(\Gamma_0 \subseteq \Gamma\) y\(\Gamma_1 \subseteq \Gamma\),\(\Gamma_0 \cup \Gamma_1 \subseteq \Gamma\). De ahí\(\Gamma\) que sea inconsistente. ◻