8.8: Nociones teóricas de prueba
- Page ID
- 103647
Así como hemos definido una serie de nociones semánticas importantes (validez, vinculación, satisfacción), ahora definimos nociones teóricas de prueba correspondientes. Estos no se definen por la apelación a la satisfacción de las sentencias en las estructuras, sino por la apelación a la derivabilidad o no derivabilidad de ciertos secuentes. Fue un descubrimiento importante que estas nociones coincidan. Lo que hacen es el contenido del teorema de solidez e integridad.
Definición\(\PageIndex{1}\): Theorems
Una oración\(A\) es un teorema si hay una derivación en\(\Log{LK}\) del secuente\(\quad \Sequent A\). Escribimos\(\Proves A\) si\(A\) es un teorema y\(\ProvesN A\) si no lo es.
Definición\(\PageIndex{2}\): Derivability
Una oración\(A\) es derivable de un conjunto de oraciones\(\Gamma\),\(\Gamma \Proves A\), si hay un subconjunto finito\(\Gamma_0 \subseteq \Gamma\) y una secuencia\(\Gamma_0'\) de las oraciones de\(\Gamma_0\) tal manera que\(\Log{LK}\) deriva\(\Gamma_0' \Sequent A\). Si no\(A\) es derivable de\(\Gamma\) escribimos\(\Gamma \ProvesN A\).
Debido a las reglas de contracción, debilitamiento e intercambio, el orden y el número de oraciones en\(\Gamma_0'\) no importa: si un secuente\(\Gamma_0' \Sequent A\) es derivable, entonces también lo es\(\Gamma_0'' \Sequent A\) para cualquiera\(\Gamma_0''\) que contenga las mismas oraciones que \(\Gamma_0'\). Por ejemplo, si\(\Gamma_0 = \{B, C\}\) entonces ambos\(\Gamma_0' = \tuple{B, B, C}\) y\(\Gamma_0'' = \tuple{C, C, B}\) son secuencias que contienen solo las oraciones en\(\Gamma_0\). Si un secuente que contiene uno es derivable, también lo es el otro, por ejemplo:
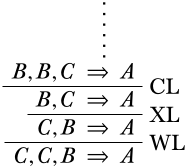
A partir de ahora diremos que si\(\Gamma_0\) es un conjunto finito de oraciones entonces\(\Gamma_0 \Sequent A\) es cualquier secuente donde el antecedente sea una secuencia de oraciones\(\Gamma_0\) e incluya tácitamente contracciones, intercambios y debilitaciones si es necesario.
Definición\(\PageIndex{3}\): Consistency
Un conjunto de oraciones\(\Gamma\) es inconsistente si hay un subconjunto finito\(\Gamma_0 \subseteq \Gamma\) tal que\(\Log{LK}\) deriva\(\Gamma_0 \Sequent \quad\). Si no\(\Gamma\) es inconsistente, es decir, si por cada finito\(\Gamma_0 \subseteq \Gamma\),\(\Log{LK}\) no deriva\(\Gamma_0 \Sequent \quad\), decimos que es consistente.
Proposición\(\PageIndex{1}\): Reflexivity
Si\(A \in \Gamma\), entonces\(\Gamma \Proves A\).
Prueba. El secuente inicial\(A \Sequent A\) es derivable, y\(\{A\} \subseteq \Gamma\). ◻
Proposición\(\PageIndex{2}\): Monotony
Si\(\Gamma \subseteq \Delta\) y\(\Gamma \Proves A\), entonces\(\Delta \Proves A\).
Prueba. Supongamos\(\Gamma \Proves A\), es decir, hay un\(\Gamma_0 \subseteq \Gamma\) tal finito que\(\Gamma_0 \Sequent A\) es derivable. Ya que\(\Gamma \subseteq \Delta\), entonces también\(\Gamma_0\) es un subconjunto finito de\(\Delta\). La derivación de\(\Gamma_0 \Sequent A\) así también muestra\(\Delta \Proves A\). ◻
Proposición\(\PageIndex{3}\): Transitivity
Si\(\Gamma \Proves A\) y\(\{A\} \cup \Delta \Proves B\), entonces\(\Gamma \cup \Delta \Proves B\).
Prueba. Si\(\Gamma \Proves A\), hay un finito\(\Gamma_0 \subseteq \Gamma\) y una derivación\(\pi_0\) de\(\Gamma_0 \Sequent A\). Si\(\{A\} \cup \Delta \Proves B\), entonces para algún subconjunto finito\(\Delta_0 \subseteq \Delta\), hay una derivación\(\pi_1\) de\(A, \Delta_0 \Sequent B\). Considere la siguiente derivación:
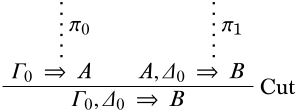
Ya que\(\Gamma_0 \cup \Delta_0 \subseteq \Gamma \cup \Delta\), esto demuestra\(\Gamma \cup \Delta \Proves B\). ◻
Tenga en cuenta que esto significa que en particular si\(\Gamma \Proves A\) y\(A \Proves B\), entonces\(\Gamma \Proves B\). De ello se deduce también que si\(A_1, \dots, A_n \Proves B\) y\(\Gamma \Proves A_i\) para cada uno\(i\), entonces\(\Gamma \Proves B\).
\(\Gamma\)es inconsistente iff\(\Gamma \Proves {A}\) para cada oración\(A\).
Prueba. Ejercicio. ◻
Problema\(\PageIndex{1}\)
Proponer Proposición\(\PageIndex{4}\).
Proposición\(\PageIndex{5}\): Compactness
-
Si\(\Gamma \Proves A\) entonces hay un subconjunto finito\(\Gamma_0 \subseteq \Gamma\) tal que\(\Gamma_0 \Proves A\).
-
Si cada subconjunto finito de\(\Gamma\) es consistente, entonces\(\Gamma\) es consistente.
Prueba.
-
Si\(\Gamma \Proves A\), entonces hay un subconjunto finito\(\Gamma_0 \subseteq \Gamma\) tal que el secuente\(\Gamma_0 \Sequent A\) tiene una derivación. En consecuencia,\(\Gamma_0 \Proves A\).
-
Si\(\Gamma\) es inconsistente, hay un subconjunto finito\(\Gamma_0 \subseteq \Gamma\) tal que\(\Log{LK}\) deriva\(\Gamma_0 \Sequent \quad\). Pero entonces\(\Gamma_0\) es un subconjunto finito de\(\Gamma\) eso es inconsistente.
◻


