9.12: Derivaciones con predicado de identidad

Última actualización
Guardar como PDF

Page ID: 103641

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Template:MathJaxZach

Las derivaciones con predicado de identidad requieren reglas de inferencia adicionales.

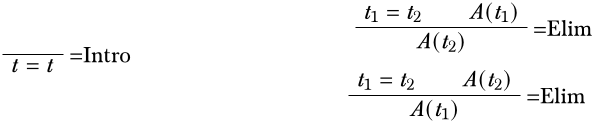
9.12.1.png

En las reglas anteriores,\(t\),\(t_1\), y\(t_2\) son términos cerrados. La\(\Intro{\eq[][]}\) regla nos permite derivar cualquier declaración de identidad de la forma de\(\eq[t][t]\) plano, a partir de ninguna suposición.

Ejemplo\(\PageIndex{1}\)

Si\(s\) y\(t\) son términos cerrados, entonces\(A(s), \eq[s][t] \Proves A(t)\):

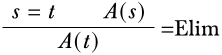
9.12.2.png

Esto puede ser familiar como el “principio de sustituibilidad de las mismas”, o Ley de Leibniz.

Problema\(\PageIndex{1}\)

Demostrar que\(=\) es tanto simétrico como transitivo, es decir, dar derivaciones de\(\lforall{x}{\lforall{y}{(\eq[x][y] \lif \eq[y][x])}}\) y\(\lforall{x}{\lforall{y}{\lforall{z}{}((\eq[x][y] \land \eq[y][z]) \lif \eq[x][z])}}\)

Ejemplo\(\PageIndex{2}\)

Derivamos la sentencia

\[\lforall{x}{\lforall{y}{((A(x) \land A(y)) \lif \eq[x][y])}} \nonumber\]

de la sentencia

\[\lexists{x}{\lforall{y}{(A(y) \lif \eq[y][x])}}\nonumber\]

Desarrollamos la derivación hacia atrás:

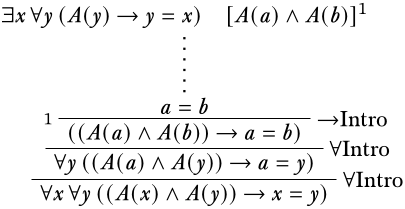
9.12.3.png

Ahora tendremos que usar el supuesto principal: al tratarse de una fórmula existencial, utilizamos\(\Elim{\lexists{}{}}\) para derivar la conclusión intermediaria\(\eq[a][b]\).

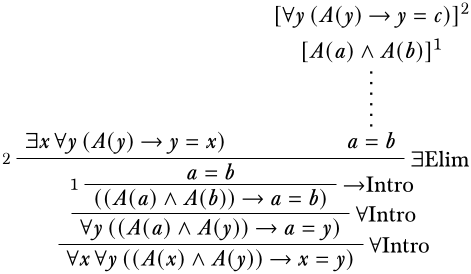
9.12.4.png

La subderivación en la parte superior derecha se completa utilizando sus supuestos para mostrar eso\(\eq[a][c]\) y\(\eq[b][c]\). Esto requiere dos derivaciones separadas. La derivación para\(\eq[a][c]\) es la siguiente:

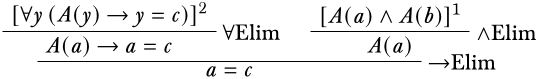
9.12.5.png

De\(\eq[a][c]\) y\(\eq[b][c]\) derivamos\(\eq[a][b]\) por\(\Elim{\eq[][]}\).

Problema\(\PageIndex{2}\)

Dar derivaciones de las siguientes fórmulas:

\(\lforall{x}{\lforall{y}{((\eq[x][y] \land A(x)) \lif A(y))}}\)
\(\lexists{x}{A(x)} \land \lforall{y}{\lforall{z}{((A(y) \land A(z)) \lif \eq[y][z])}} \lif \lexists{x}{(A(x) \land \lforall{y}{(A(y) \lif \eq[y][x])})}\)