9.11: Solidez
- Page ID
- 103626
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Un sistema de derivación, como la deducción natural, es sólido si no puede derivar cosas que realmente no siguen. Por lo tanto, la solidez es una especie de propiedad de seguridad garantizada para los sistemas de derivación. Dependiendo de qué prueba de propiedad teórica esté en cuestión, nos gustaría saber por ejemplo, que
- toda oración derivable es válida;
- si una oración es derivable de algunas otras, también es consecuencia de ellas;
- si un conjunto de oraciones es inconsistente, es insatisfactorio.
Estas son propiedades importantes de un sistema de derivación. Si alguno de ellos no se sostiene, el sistema de derivación es deficiente—derivaría demasiado. En consecuencia, es de suma importancia establecer la solidez de un sistema de derivación.
Teorema\(\PageIndex{1}\): Soundness
Si\(A\) es derivable de los supuestos no descargados\(\Gamma\), entonces\(\Gamma \Entails A\).
Prueba. Dejar\(\delta\) ser una derivación de\(A\). Se procede por inducción sobre el número de inferencias en\(\delta\).
Para la base de inducción mostramos el reclamo si el número de inferencias es\(0\). En este caso,\(\delta\) consiste únicamente en una sola oración\(A\), es decir, una suposición. Esa suposición no está descargada, ya que las suposiciones sólo pueden ser descargadas por inferencias, y no hay inferencias. Entonces, cualquier estructura\(\Struct{M}\) que satisfaga todos los supuestos no descargados de la prueba también satisface\(A\).
Ahora para el paso inductivo. Supongamos que\(\delta\) contiene\(n\) inferencias. La (s) premisa (s) de la inferencia más baja se derivan utilizando subderivaciones, cada una de las cuales contiene menos de\(n\) inferencias. Asumimos la hipótesis de inducción: Las premisas de la inferencia más baja se derivan de los supuestos no descargados de las subderivaciones que terminan en esas premisas. Tenemos que demostrar que la conclusión se\(A\) desprende de los supuestos no descargados de toda la prueba.
Distinguimos los casos según el tipo de inferencia más baja. Primero, consideramos las posibles inferencias con una sola premisa.
-
Supongamos que la última inferencia es\(\Intro{\lnot}\): La derivación tiene la forma
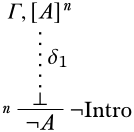
Por hipótesis inductiva,\(\lfalse\) se desprende de los supuestos no descargados\(\Gamma \cup \{A\}\) de\(\delta_1\). Considera una estructura\(\Struct{M}\). Tenemos que demostrar eso, si\(\Sat{M}{\Gamma}\), entonces\(\Sat{M}{\lnot A}\). Supongamos que para reductio eso\(\Sat{M}{\Gamma}\), pero\(\SatN{M}{\lnot A}\), es decir,\(\Sat{M}{A}\). Esto significaría eso\(\Sat{M}{\Gamma \cup \{A\}}\). Esto es contrario a nuestra hipótesis inductiva. Entonces,\(\Sat{M}{\lnot A}\).
-
La última inferencia es\(\Elim{\land}\): Hay dos variantes:\(A\) o\(B\) pueden inferirse de la premisa\(A \land B\). Considera el primer caso. La derivación\(\delta\) se ve así:
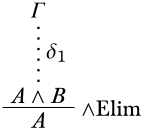
Por hipótesis inductiva,\(A \land B\) se desprende de los supuestos no descargados\(\Gamma\) de\(\delta_1\). Considera una estructura\(\Struct{M}\). Tenemos que demostrar eso, si\(\Sat{M}{\Gamma}\), entonces\(\Sat{M}{A}\). Supongamos\(\Sat{M}{\Gamma}\). Por nuestra hipótesis inductiva (\(\Gamma \Entails A \land B\)), lo sabemos\(\Sat{M}{A \land B}\). Por definición,\(\Sat{M}{A \land B}\) iff\(\Sat{M}{A}\) y\(\Sat{M}{B}\). (El caso en el\(B\) que se deduce\(A \land B\) se maneja de manera similar.)
-
La última inferencia es\(\Intro{\lor}\): Hay dos variantes: se\(A \lor B\) pueden inferir de la premisa\(A\) o de la premisa\(B\). Considera el primer caso. La derivación tiene la forma
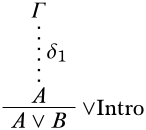
Por hipótesis inductiva,\(A\) se desprende de los supuestos no descargados\(\Gamma\) de\(\delta_1\). Considera una estructura\(\Struct{M}\). Tenemos que demostrar eso, si\(\Sat{M}{\Gamma}\), entonces\(\Sat{M}{A \lor B}\). Supongamos\(\Sat{M}{\Gamma}\); entonces\(\Sat{M}{A}\) desde\(\Gamma \Entails A\) (la hipótesis inductiva). Por lo que también debe ser el caso que\(\Sat{M}{A \lor B}\). (El caso en el\(A \lor B\) que se deduce\(B\) se maneja de manera similar.)
-
La última inferencia\(A \lif B\) es\(\Intro{\lif}\): se infiere de una subprueba con suposición\(A\) y conclusión\(B\), es decir,
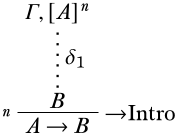
Por hipótesis inductiva,\(B\) se desprende de los supuestos no descargados de\(\delta_1\), es decir,\(\Gamma \cup \{A\} \Entails B\). Considera una estructura\(\Struct{M}\). Los supuestos no descargados de\(\delta\) son justos\(\Gamma\), ya que\(A\) se descarga en la última inferencia. Entonces tenemos que demostrar eso\(\Gamma \Entails A \lif B\). Para reductio, supongamos que para alguna estructura\(\Struct{M}\),\(\Sat{M}{\Gamma}\) pero\(\SatN{M}{A \lif B}\). Entonces,\(\Sat{M}{A}\) y\(\SatN{M}{B}\). Pero por hipótesis,\(B\) es una consecuencia de\(\Gamma \cup \{A\}\), es decir,\(\Sat{M}{B}\), que es una contradicción. Entonces,\(\Gamma \Entails A \lif B\).
-
La última inferencia es\(\FalseInt\): Aquí,\(\delta\) termina en
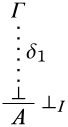
Por hipótesis de inducción,\(\Gamma \Entails \lfalse\). Tenemos que demostrarlo\(\Gamma \Entails A\). Supongamos que no; entonces para algunos\({\Struct{M}}\) tenemos\(\Sat{M}{\Gamma}\) y\(\SatN{M}{A}\). Pero siempre lo hemos hecho\(\SatN{M}{\lfalse}\), así que esto significaría eso\(\Gamma \EntailsN \lfalse\), contrario a la hipótesis de inducción.
-
La última inferencia es\(\FalseCl\): Ejercicio.
-
La última inferencia es\(\Intro{\lforall{}{}}\): Entonces\(\delta\) tiene la forma
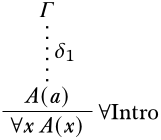
La premisa\(A(a)\) es consecuencia de los supuestos no descargados\(\Gamma\) por hipótesis de inducción. Considera alguna estructura,\(\Struct{M}\), tal que\(\Sat{M}{\Gamma}\). Tenemos que demostrarlo\(\Sat{M}{\lforall{x}{A(x)}}\). Ya que\(\lforall{x}{A(x)}\) es una oración, esto significa que tenemos que demostrar que para cada asignación de variables\(s\),\(\Sat[,s]{M}{A(x)}\) (Proposición 5.12.4). Ya que\(\Gamma\) consiste íntegramente en oraciones,\(\Sat[,s]{M}{B}\) para todos\(B \in \Gamma\) por Definición 5.11.4. Seamos\(\Struct{M'}\) como\(\Struct{M}\) excepto eso\(\Assign{a}{M'} = s(x)\). Ya que\(a\) no ocurre en\(\Gamma\),\(\Sat{M'}{\Gamma}\) por Corolario 5.13.1. Ya que\(\Gamma \Entails A(a)\),\(\Sat{M'}{A(a)}\). Ya que\(A(a)\) es una oración,\(\Sat[,s]{M'}{A(a)}\) por la Proposición 5.12.3. \(\Sat[,s]{M'}{A(x)}\)iff\(\Sat{M'}{A(a)}\) por la Proposición 5.13.3 (recuerda que\(A(a)\) es justo\(\Subst{A(x)}{a}{x}\)). Entonces,\(\Sat[,s]{M'}{A(x)}\). Ya que\(a\) no ocurre en\(A(x)\), por la Proposición 5.13.1,\(\Sat[,s]{M}{A(x)}\). Pero\(s\) era una asignación variable arbitraria, entonces\(\Sat{M}{\lforall{x}{A(x)}}\).
-
La última inferencia es\(\Intro{\lexists{}{}}\): Ejercicio.
-
La última inferencia es\(\Elim{\forall}\): Ejercicio.
Ahora consideremos las posibles inferencias con varias premisas:\(\Elim{\lor}\),\(\Intro{\land}\),\(\Elim{\lif}\), and \(\Elim{\lexists{}{}}\).
-
La última inferencia es\(\Intro{\land}\). \(A \land B\)se infiere de las premisas\(A\)\(B\) y y\(\delta\) tiene la forma
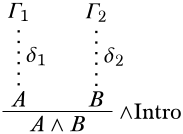
Por hipótesis de inducción,\(A\) se desprende de los supuestos no descargados\(\Gamma_1\) de\(\delta_1\) y se\(B\) desprende de los supuestos no descargados\(\Gamma_2\) de\(\delta_2\). Los supuestos no descargados de\(\delta\) son\(\Gamma_1 \cup \Gamma_2\), así que tenemos que demostrarlo\(\Gamma_1 \cup \Gamma_2 \Entails A \land B\). Considerar una estructura\(\Struct{M}\) con\(\Sat{M}{\Gamma_1 \cup \Gamma_2}\). Ya que\(\Sat{M}{\Gamma_1}\), debe darse el caso que\(\Sat{M}{A}\) como\(\Gamma_1 \Entails A\), y desde\(\Sat{M}{\Gamma_2}\),\(\Sat{M}{B}\) desde entonces\(\Gamma_2 \Entails B\). Juntos,\(\Sat{M}{A \land B}\).
-
La última inferencia es\(\Elim{\lor}\): Ejercicio.
-
La última inferencia es\(\Elim{\lif}\). \(B\)se infiere de las premisas\(A \lif B\) y\(A\). La derivación\(\delta\) se ve así:
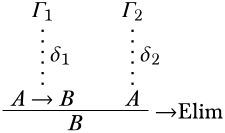
Por hipótesis de inducción,\(A \lif B\) se desprende de los supuestos no descargados\(\Gamma_1\) de\(\delta_1\) y se\(A\) desprende de los supuestos no descargados\(\Gamma_2\) de\(\delta_2\). Considera una estructura\(\Struct{M}\). Tenemos que demostrar eso, si\(\Sat{M}{\Gamma_1 \cup \Gamma_2}\), entonces\(\Sat{M}{B}\). Supongamos\(\Sat{M}{\Gamma_1 \cup \Gamma_2}\). Ya que\(\Gamma_1 \Entails A \lif B\),\(\Sat{M}{A \lif B}\). Ya que\(\Gamma_2 \Entails A\), tenemos\(\Sat{M}{A}\). Esto quiere decir que\(\Sat{M}{B}\) (Por si\(\SatN{M}{B}\), ya que\(\Sat{M}{A}\), tendríamos\(\SatN{M}{A \lif B}\), contradiciendo\(\Sat{M}{A \lif B}\)).
-
La última inferencia es\(\Elim{\lnot}\): Ejercicio.
-
La última inferencia es\(\Elim{\lexists{}{}}\): Ejercicio.
◻
Problema\(\PageIndex{1}\)
Completar la prueba del Teorema\(\PageIndex{1}\).
Si\(\Gamma\) es satisfecha, entonces es consistente.
Prueba. Demostramos lo contrapositivo. Supongamos que eso no\(\Gamma\) es consistente. Entonces\(\Gamma \Proves \lfalse\), es decir, hay una derivación\(\lfalse\) de supuestos no descargados en\(\Gamma\). Por teorema\(\PageIndex{1}\), cualquier estructura\(\Struct{M}\) que satisfaga\(\Gamma\) debe satisfacer\(\lfalse\). Ya que\(\SatN{M}{\lfalse}\) para cada estructura\(\Struct{M}\), ninguna\(\Struct{M}\) puede satisfacer\(\Gamma\), es decir, no\(\Gamma\) es satisfecha. ◻


