9.4: Derivaciones
- Page ID
- 103649
Hemos dicho lo que es una suposición, y hemos dado las reglas de inferencia. Las derivaciones en deducción natural se generan inductivamente a partir de estas: cada derivación es una suposición por sí misma, o consiste en una, dos o tres derivaciones seguidas de una inferencia correcta.
Definición\(\PageIndex{1}\): Derivation
Una derivación de una oración\(A\) a partir de suposiciones\(\Gamma\) es un árbol de oraciones que cumple las siguientes condiciones:
-
Las oraciones más altas del árbol están en\(\Gamma\) o son descargadas por una inferencia en el árbol.
-
La frase más baja del árbol es\(A\).
-
Toda oración en el árbol excepto la oración\(A\) en la parte inferior es una premisa de una correcta aplicación de una regla de inferencia cuya conclusión se encuentra directamente debajo de esa oración en el árbol.
Entonces decimos que\(A\) es la conclusión de la derivación y de eso\(A\) es derivable\(\Gamma\).
Ejemplo\(\PageIndex{1}\)
Cada suposición por sí misma es una derivación. Entonces, e.g.,\(C\) por sí mismo es una derivación, y así es\(D\) por sí misma. Podemos obtener una nueva derivación de estos aplicando, digamos, la\(\Intro{\land}\) regla,
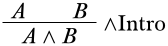
Estas reglas están destinadas a ser generales: podemos sustituir el\(A\) y\(B\) en él con cualquier oración, por ejemplo, por\(C\) y\(D\). Entonces la conclusión sería\(C \land D\), y así
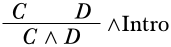
es una derivación correcta. Por supuesto, también podemos cambiar los supuestos, de modo que eso\(D\) juega el papel de\(A\) y\(C\) el de\(B\). Así,
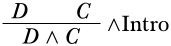
es también una derivación correcta.
Ahora podemos aplicar otra regla, digamos,\(\Intro{\lif}\), que nos permite concluir un condicional y nos permite descargar cualquier suposición que sea idéntica al antecedente de ese condicional. Entonces ambas de las siguientes serían derivaciones correctas:
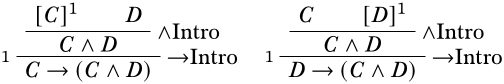
Recuerda que la descarga de suposiciones es un permiso, no un requisito: no tenemos que descargar los supuestos. En particular, podemos aplicar una regla aunque los supuestos no estén presentes en la derivación. Por ejemplo, lo siguiente es legal, aunque no hay supuesto\(A\) para ser dado de baja: