9.5: Ejemplos de Derivaciones

Template:MathJaxZach

Ejemplo\(\PageIndex{1}\)

Demos una derivación de la oración\((A \land B) \lif A\).

Comenzamos por escribir la conclusión deseada en la parte inferior de la derivación.

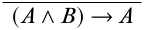
A continuación, necesitamos averiguar qué tipo de inferencia podría resultar en una oración de esta forma. El principal operador de la conclusión es\(\lif\), así que intentaremos llegar a la conclusión usando la\(\Intro{\lif}\) regla. Lo mejor es anotar los supuestos involucrados y etiquetar las reglas de inferencia a medida que avanza, por lo que es fácil ver si todos los supuestos han sido dados de alta al final de la prueba.

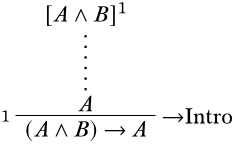
Ahora necesitamos rellenar los pasos desde el supuesto\(A \land B\) hasta\(A\). Ya que solo tenemos un conectivo con el que lidiar\(\land\),, debemos usar la regla\(\land\) elim. Esto nos da la siguiente prueba:

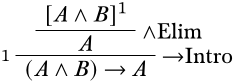
Ahora tenemos una correcta derivación de\((A \land B) \lif A\).

Ejemplo\(\PageIndex{2}\)

Ahora vamos a dar una derivación de\((\lnot A \lor B) \lif (A \lif B)\).

Comenzamos por escribir la conclusión deseada en la parte inferior de la derivación.

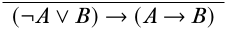
Para encontrar una regla lógica que nos pudiera dar esta conclusión, miramos las conectivas lógicas en la conclusión:\(\lnot\),\(\lor\), y\(\lif\). Solo nos importa en este momento la primera ocurencia de\(\lif\) porque es el operador principal de la oración en el final secuente, mientras que\(\lnot\),\(\lor\) y la segunda ocurre de\(\lif\) están dentro del alcance de otro conectivo, por lo que vamos a encargarse de esos más tarde. Por lo tanto, comenzamos con la\(\Intro{\lif}\) regla. Una aplicación correcta debe verse así:

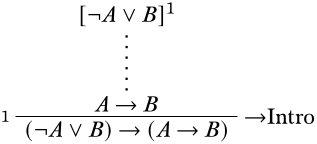
Esto nos deja con dos posibilidades para continuar. O podemos seguir trabajando de abajo hacia arriba y buscar otra aplicación de la\(\Intro{\lif}\) regla, o podemos trabajar de arriba hacia abajo y aplicar una\(\Elim{\lor}\) regla. Apliquemos este último. Utilizaremos la suposición\(\lnot A \lor B\) como la premisa más a la izquierda de\(\Elim{\lor}\). Para una aplicación válida de\(\Elim{\lor}\), las otras dos premisas deben ser idénticas a la conclusión\(A \lif B\), pero cada una puede derivarse a su vez de otra suposición, a saber, los dos desjuntos de\(\lnot A \lor B\). Entonces nuestra derivación se verá así:

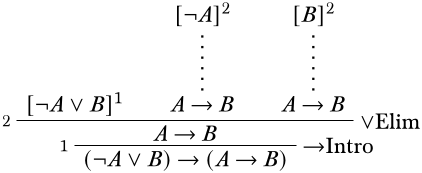
En cada una de las dos ramas de la derecha, queremos derivar\(A \lif B\), que se hace mejor usando\(\Intro{\lif}\).

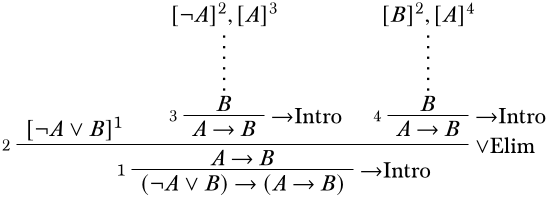
Para las dos partes faltantes de la derivación, necesitamos derivaciones de\(B\) desde\(\lnot A\) y\(A\) en el medio, y desde\(A\) y\(B\) por la izquierda. Tomemos primero el primero. \(\lnot A\)y\(A\) son las dos premisas de\(\Elim{\lnot}\):

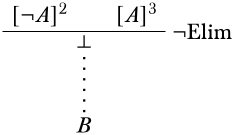
Mediante el uso\(\FalseInt\), podemos obtener\(B\) como conclusión y completar la rama.

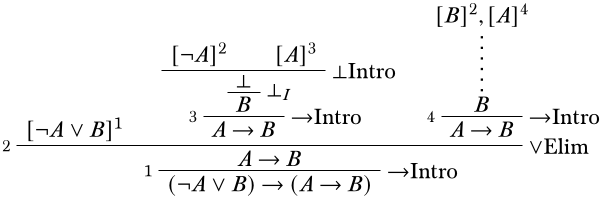
Veamos ahora la rama más a la derecha. Aquí es importante darse cuenta de que la definición de derivación permite que los supuestos sean dados de alta pero no requiere que sean. Es decir, si podemos\(B\) derivar de uno de los supuestos\(A\) y\(B\) sin usar el otro, está bien. Y\(B\) derivar de\(B\) ello es trivial:\(B\) por sí misma es tal derivación, y no se necesitan inferencias. Entonces podemos simplemente borrar la suposición\(A\).

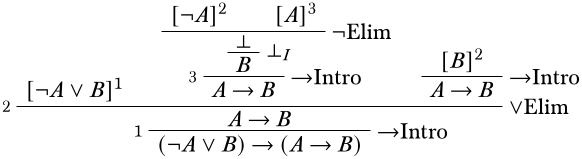
Obsérvese que en la derivación terminada, la\(\Intro{\lif}\) inferencia más a la derecha en realidad no descarga ningún supuesto.

Ejemplo\(\PageIndex{3}\)

Hasta el momento no hemos necesitado la\(\FalseCl{}\) regla. Es especial en que nos permite descargar una suposición que no es una subfórmula de la conclusión de la regla. Está estrechamente relacionado con la\(\FalseInt{}\) regla. De hecho, la\(\FalseInt{}\) regla es un caso especial de la\(\FalseCl{}\) regla—hay una lógica llamada “lógica intuicionista” en la que sólo\(\FalseInt{}\) se permite. La\(\FalseCl{}\) regla es un último recurso cuando nada más funciona. Por ejemplo, supongamos que queremos derivar\(A \lor \lnot A\). Nuestra estrategia habitual sería intentar derivar\(A \lor \lnot A\) usando\(\Intro{\lor}\). Pero esto requeriría que deriváramos\(A\) o\(\lnot A\) de ninguna suposición, y esto no se puede hacer. \(\FalseCl{}\)al rescate!

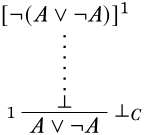
Ahora estamos buscando una derivación\(\lfalse\) de\(\lnot(A \lor \lnot A)\). Ya que\(\lfalse\) es la conclusión de que\(\Elim{\lnot}\) podríamos intentar que:

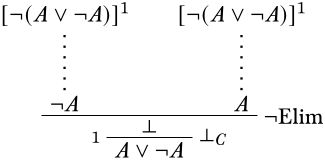
Nuestra estrategia para encontrar una derivación de\(\lnot A\) convocatorias para una aplicación de\(\Intro{\lnot}\):

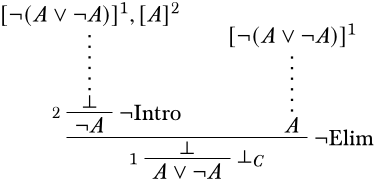
Aquí, podemos obtener\(\lfalse\) fácilmente aplicándonos\(\Elim{\lnot}\) a la suposición\(\lnot(A \lor \lnot A)\) y\(A \lor \lnot A\) que se desprende de nuestra nueva suposición\(A\) por\(\Intro{\lor}\):

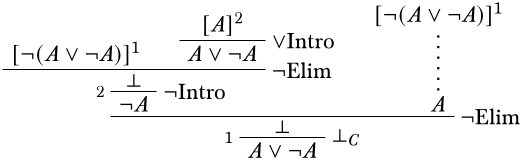
En el lado derecho usamos la misma estrategia, excepto que nos las\(A\) arreglamos\(\FalseCl\):

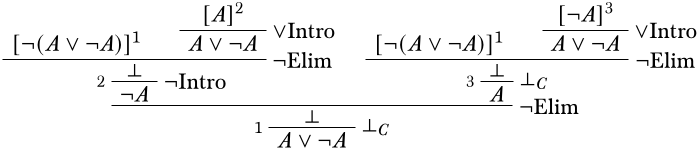
Problema\(\PageIndex{1}\)

Dar derivaciones de lo siguiente:

1. \(\lnot(A \lif B) \lif (A \land \lnot B)\)

2. \((A \lif C) \lor (B \lif C)\)de la suposición\((A \land B) \lif C\)

3. \(\lnot \lnot A \lif A\)

4. \(\lnot A \lif \lnot B\)de la suposición\(B \lif A\)

5. \(\lnot A\)de la suposición\(( A \lif \lnot A )\)

6. \(A\)a partir de los supuestos\(B \lif A\) y\(\lnot B \lif A\)