7.3: Deducción natural
- Page ID
- 103507
La deducción natural es un sistema de derivación destinado a reflejar el razonamiento real (especialmente el tipo de razonamiento regido empleado por los matemáticos). El razonamiento real procede por una serie de patrones “naturales”. Por ejemplo, la prueba por casos nos permite establecer una conclusión sobre la base de una premisa disyuntiva, estableciendo que la conclusión se deriva de cualquiera de los disjuntos. La prueba indirecta nos permite establecer una conclusión demostrando que su negación conduce a una contradicción. La prueba condicional establece una pretensión condicional “si... entonces...” demostrando que el consecuente se desprende del antecedente. La deducción natural es una formalización de algunas de estas inferencias naturales. Cada una de las conectivas lógicas y cuantificadores viene con dos reglas, una regla de introducción y una de eliminación, y cada una de ellas corresponde a uno de esos patrones de inferencia natural. Por ejemplo,\(\Intro{\lif}\) corresponde a prueba condicional, y\(\Elim{\lor}\) a prueba por casos. Una regla particularmente simple es la\(\Elim{\land}\) que permite la inferencia de\(A \land B\) a\(A\) (o\(B\)).
Una característica que distingue a la deducción natural de otros sistemas de derivación es su uso de suposiciones. Una derivación en deducción natural es un árbol de fórmulas. Una sola fórmula se encuentra en la raíz del árbol de fórmulas, y las “hojas” del árbol son fórmulas de las que se deriva la conclusión. En la deducción natural, algunas fórmulas foliares juegan un papel dentro de la derivación pero se “utilizan” para cuando la derivación llega a la conclusión. Esto corresponde a la práctica, en el razonamiento real, de introducir hipótesis que sólo permanecen vigentes por un corto tiempo. Por ejemplo, en una prueba por casos, asumimos la verdad de cada uno de los disjuntos; en la prueba condicional, asumimos la verdad del antecedente; en la prueba indirecta, asumimos la verdad de la negación de la conclusión. Esta forma de introducir supuestos hipotéticos y luego eliminarlos al servicio de establecer un paso intermedio es un sello de deducción natural. Las fórmulas a las hojas de una derivación de deducción natural se denominan supuestos, y algunas de las reglas de inferencia pueden “descargarlas”. Por ejemplo, si tenemos una derivación\(B\) de algunos supuestos que incluyen\(A\), entonces la\(\Intro{\lif}\) regla nos permite inferir\(A \lif B\) y descargar cualquier suposición de la forma\(A\). (Para realizar un seguimiento de qué supuestos se descargan en qué inferencias, etiquetamos la inferencia y los supuestos que descarga con un número). Los supuestos que permanecen sin descargar al final de la derivación son en conjunto suficientes para la verdad de la conclusión, por lo que una derivación establece que sus supuestos no descargados conllevan su conclusión.
La relación\(\Gamma \Proves A\) basada en la deducción natural sostiene si hay una derivación en la que\(A\) se encuentra la última frase en el árbol, y cada hoja que no está descargada está en\(\Gamma\). \(A\)es un teorema en deducción natural si hay una derivación en la que\(A\) se encuentra la última frase y se descargan todos los supuestos. Por ejemplo, aquí hay una derivación que muestra que\(\Proves (A \land B) \lif A\):
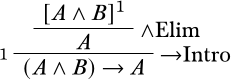
La etiqueta\(1\) indica que la suposición\(A \land B\) se descarga a la\(\Intro{\lif}\) inferencia.
Un conjunto\(\Gamma\) es inconsistente iff\(\Gamma \Proves \lfalse\) en deducción natural. La regla\(\FalseInt{}\) hace que a partir de un conjunto inconsistente, se pueda derivar cualquier oración.
Los sistemas naturales de deducción fueron desarrollados por Gerhard Gentzen y Stanisław Jaśkowski en la década de 1930, y más tarde desarrollados por Dang Prawitz y Frederic Fitch. Debido a que sus inferencias reflejan métodos naturales de prueba, es favorecida por los filósofos. Las versiones desarrolladas por Fitch se utilizan a menudo en libros de texto de lógica introductoria. En la filosofía de la lógica, las reglas de deducción natural a veces se han tomado para dar los significados de los operadores lógicos (“semántica probadora-teórica”).


