12.5: Representación Unaria de Números
- Page ID
- 103664
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Las máquinas Turing trabajan en secuencias de símbolos escritos en su cinta. Dependiendo del alfabeto que utilice una máquina Turing, estas secuencias de símbolos pueden representar varias entradas y salidas. De particular interés, por supuesto, son las máquinas Turing que computan funciones aritméticas, es decir, funciones de números naturales. Una forma sencilla de representar números enteros positivos es codificándolos como secuencias de un solo símbolo\(\TMstroke\). Si\(n \in \Nat\), deja\(\TMstroke^n\) ser la secuencia vacía si\(n = 0\), y de lo contrario la secuencia que consiste en exactamente\(n\)\(\TMstroke\)'s.
Definición\(\PageIndex{1}\): Computation
Una máquina Turing\(M\) calcula la función\(f\colon \Nat^n \to \Nat\) iff\(M\) se detiene en la entrada\[\TMstroke^{k_1} \TMblank \TMstroke^{k_2} \TMblank \dots \TMblank \TMstroke^{k_n}\nonumber\] con la salida\(\TMstroke^{f(k_1, \dots, k_n)}\).
Ejemplo\(\PageIndex{1}\)
Adición: Construye una máquina que, cuando se le da una entrada de dos cadenas no vacías de\(\TMstroke\)'s de longitud\(n\) y\(m\), calcula la función\(f(n,m) = n + m\).
Queremos llegar a una máquina que comience con dos bloques de trazos en la cinta y se detenga con un bloque de trazos. Primero necesitamos un método para llevar a cabo. Los trazos de entrada están separados por un espacio en blanco, por lo que un método sería escribir un trazo en el cuadrado que contiene el espacio en blanco, y borrar el primer (o último) trazo. Esto daría como resultado un bloque de\(n + m\)\(\TMstroke\)'s Alternativamente, podríamos proceder de manera similar a la máquina dobladora, borrando un trazo del primer bloque, y agregando uno al segundo bloque de trazos hasta que el primer bloque haya sido eliminado por completo. Procederemos con el ejemplo anterior.
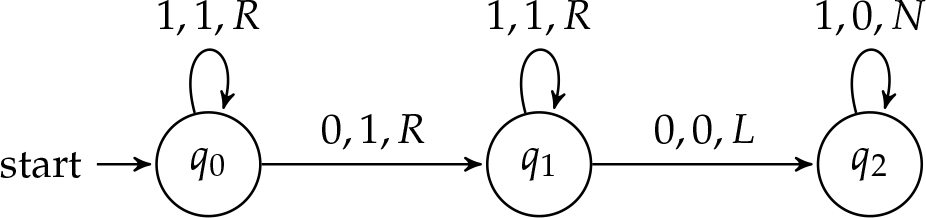
Problema\(\PageIndex{1}\)
Trace a través de las configuraciones de la máquina para la entrada\(\tuple{3,5}\).
Problema\(\PageIndex{2}\)
Resta: Diseñar una máquina Turing que cuando se le da una entrada de dos cadenas de trazos de longitud no vacías\(n\) y\(m\), donde\(n > m\), compute la función\(f(n,m) = n - m\).
Problema\(\PageIndex{3}\)
Igualdad: Diseñar una máquina Turing para calcular la siguiente función:\[\fn{equality}(x,y) = \begin{cases} \text{1} & \text{if $x = y$} \\ \text{0} & \text{if $x \neq y$} \end{cases}\nonumber\] donde\(x\) y\(y\) son enteros mayores que\(0\).
Problema\(\PageIndex{4}\)
Diseñe una máquina Turing para calcular la función\(\min(x,y)\) donde\(x\) y\(y\) son enteros positivos representados en la cinta por cadenas de\(\TMstroke\)'s separadas por a\(\TMblank\). Se pueden utilizar símbolos adicionales en el alfabeto de la máquina.
La función\(\min\) selecciona el valor más pequeño de sus argumentos\(\min(3,5)=3\), así\(\min(20,16)=16\),\(\min(4,4)=4\), y así sucesivamente.


