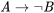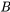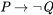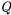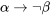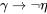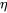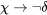3: La lógica formal en la filosofía
- Page ID
- 102756
En este capítulo se discuten algunas cuestiones filosóficas relativas a la naturaleza de la lógica formal. Se prestará especial atención al concepto de forma lógica, al objetivo de la lógica formal en la captura de la forma lógica y a la explicación de validez en términos de forma lógica. Veremos cómo esta comprensión de la noción de validez nos permite identificar lo que llamamos falacias formales, que son errores en un argumento por su forma lógica. También discutiremos algunos problemas filosóficos sobre la naturaleza de las formas lógicas. En aras de la simplicidad, nuestro enfoque estará en la lógica proposicional. Pero muchos de los resultados a discutir no dependen de esta elección, y son aplicables a sistemas lógicos más avanzados.
Lógica, Validez y Formas Lógicas
Diferentes ciencias tienen diferentes temas: la física trata de descubrir las propiedades de la materia, la historia tiene como objetivo descubrir lo que sucedió en el pasado, la biología estudia el desarrollo y evolución de los organismos vivos, las matemáticas son, o al menos parecen ser, sobre números, conjuntos, espacios geométricos y como. Pero, ¿qué es lo que la lógica investiga? ¿Qué es, en efecto, la lógica?
Se trata de una cuestión esencialmente filosófica, pero su respuesta requiere una reflexión sobre el estado y el comportamiento de las reglas lógicas e inferencias. Los libros de texto suelen presentar la lógica como la ciencia de la relación de consecuencia que se mantiene entre las premisas y la conclusión de un argumento válido, donde un argumento es válido si no es posible que sus premisas sean verdaderas y la conclusión falsa. Si la lógica es la ciencia de la relación de consecuencia que se mantiene entre las premisas y la conclusión de un argumento válido, podemos decir que los lógicos se preocuparán de si una conclusión de un argumento es o no una consecuencia de sus premisas.
Examinemos con más cuidado la noción de validez. Por ejemplo, considere el siguiente argumento:
- Si Alex es besugo, entonces Alex no es una rosa.
- Alex es una rosa.
Alex no es un besugo.
Se puede demostrar que no es posible que (1) y (2) sean verdaderos aún (3) falsos. De ahí que todo el argumento sea válido. Por conveniencia, representemos cada frase del argumento en la lógica proposicional estándar, que tiene como objetivo analizar la estructura y el significado de diversas proposiciones. Para ello, primero debemos introducir el lenguaje de nuestra lógica.
\[(\neg )\]
Así, si usamos A para “Alex es un besugo”, podemos representar (1) con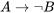 , y representar nuestro argumento anterior (1) - (3) de la siguiente manera:
, y representar nuestro argumento anterior (1) - (3) de la siguiente manera:
Pero, recordemos, nuestro objetivo era examinar por qué este argumento, si acaso, es válido. La mera representación de “no” por “ ” y “si... entonces” por “
” y “si... entonces” por “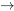 ” no será suficiente para verificar la validez o invalidez de un argumento dado: también necesitamos saber qué significan estos símbolos y las proposiciones que expresan. Pero, ¿cómo podemos especificar el significado de “
” no será suficiente para verificar la validez o invalidez de un argumento dado: también necesitamos saber qué significan estos símbolos y las proposiciones que expresan. Pero, ¿cómo podemos especificar el significado de “ ” y “
” y “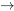 ”?
”?
Es plausible decir que si A es verdad, entonces su negación es falsa, y viceversa. Por ejemplo, si “Alex es una rosa” es cierto, entonces “Alex no es una rosa” es falso. Esto nos da el significado de “ ”. Podemos representar esta información sobre el significado de la negación en términos de una tabla de verdad de la siguiente manera (con T que simboliza verdadero y F falso):
”. Podemos representar esta información sobre el significado de la negación en términos de una tabla de verdad de la siguiente manera (con T que simboliza verdadero y F falso):
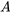 |
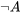 |
|---|---|
| T | F |
| F | T |
Aquí, podemos leer cada fila de la tabla de la verdad como una forma en que el mundo podría ser. Es decir, en situaciones o mundos posibles donde A es verdad (por ejemplo, donde Alex es efectivamente un besugo),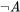 es falso (es falso que Alex sea besugo); y viceversa. Así interpretada, una tabla de la verdad nos da las situaciones en las que una proposición como A es verdadera, y aquellas en las que es falsa. Además, nos dice en qué situaciones
es falso (es falso que Alex sea besugo); y viceversa. Así interpretada, una tabla de la verdad nos da las situaciones en las que una proposición como A es verdadera, y aquellas en las que es falsa. Además, nos dice en qué situaciones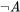 es verdad, y en qué situaciones es falsa.
es verdad, y en qué situaciones es falsa.
De manera similar, podemos especificar el significado de “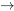 ” especificando las situaciones en las que las proposiciones condicionales de la forma “
” especificando las situaciones en las que las proposiciones condicionales de la forma “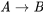 ” son verdaderas o falsas. Aquí está la tabla de verdad estándar para “
” son verdaderas o falsas. Aquí está la tabla de verdad estándar para “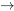 ”:
”:
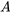 |
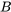 |
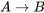 |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Como puede verse, sólo hay una fila en la que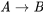 es falsa; es decir, la segunda fila en la que lo consecuente es falso, pero el antecedente es verdadero. Como nos dice la primera fila, si tanto A como B son verdaderas, entonces también lo es
es falsa; es decir, la segunda fila en la que lo consecuente es falso, pero el antecedente es verdadero. Como nos dice la primera fila, si tanto A como B son verdaderas, entonces también lo es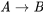 . Además, las filas tercera y cuarta nos dicen que si el antecedente es falso, entonces todo el condicional es verdadero, independientemente de que el consecuente sea verdadero o falso. De ahí que todos los condicionales con falsos antecedentes sean ciertos.
. Además, las filas tercera y cuarta nos dicen que si el antecedente es falso, entonces todo el condicional es verdadero, independientemente de que el consecuente sea verdadero o falso. De ahí que todos los condicionales con falsos antecedentes sean ciertos.
Pero, ¿cómo es posible que un condicional sea cierto si su antecedente es falso? Aquí hay una sugerencia para responder a esta pregunta: si tu suposición es falsa, entonces puedes concluir legítimamente lo que quieras. Por ejemplo, si asumes que Ámsterdam es la capital de Inglaterra, puedes concluir legítimamente cualquier cosa; no importa si es verdadera o falsa. Así, desde el supuesto de que Ámsterdam es la capital de Inglaterra, se puede concluir que París es la capital de Francia. También se puede concluir que París es la capital de Brasil.
Podemos ver que una pieza importante de información que transmiten las tablas de verdad se refiere a cómo la verdad o falsedad de oraciones complejas como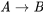 y
y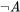 depende de la verdad o falsedad de las letras proposicionales que contienen: la verdad o falsedad de
depende de la verdad o falsedad de las letras proposicionales que contienen: la verdad o falsedad de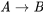 depende únicamente de la verdad o falsedad de A y de B. De igual manera, la verdad o falsedad de
depende únicamente de la verdad o falsedad de A y de B. De igual manera, la verdad o falsedad de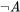 depende únicamente de la de A.
depende únicamente de la de A.
Ahora estamos en condiciones de verificar si nuestro argumento (1) - (3) es válido o no. Y, como veremos en un momento, la validez o invalidez de un argumento depende del significado de los conectivos lógicos (como “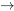 ” y “
” y “ ”) que se especifica por las tablas de verdad correspondientes. En otras palabras, si las tablas de verdad de estos conectivos fueran diferentes a lo que realmente son, tendríamos una colección diferente de argumentos válidos.
”) que se especifica por las tablas de verdad correspondientes. En otras palabras, si las tablas de verdad de estos conectivos fueran diferentes a lo que realmente son, tendríamos una colección diferente de argumentos válidos.
Definimos un argumento como válido si no es posible que sus premisas sean verdaderas y la conclusión falsa. Al diseñar una tabla de verdad, podemos ver bajo qué condiciones las premisas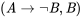 y la conclusión
y la conclusión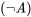 de nuestro argumento (1) - (3) son verdaderas o falsas:
de nuestro argumento (1) - (3) son verdaderas o falsas:
 |
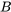 |
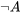 |
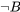 |
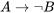 |
|---|---|---|---|---|
| T | T | F | F | F |
| T | F | F | T | T |
| F | T | T | F | T |
| F | F | T | T | T |
Ya que en la tabla de verdad anterior, no hay fila en la que las premisas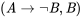 sean verdaderas y la conclusión
sean verdaderas y la conclusión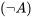 falsa, el argumento es válido. La única fila en la que ambas premisas son verdaderas es la tercera fila, y en esa fila la conclusión también es cierta. Es decir, no hay mundo ni situación en la que (1) y (2) sean verdaderos, pero (3) no lo es. Esto solo quiere decir que el argumento es válido.
falsa, el argumento es válido. La única fila en la que ambas premisas son verdaderas es la tercera fila, y en esa fila la conclusión también es cierta. Es decir, no hay mundo ni situación en la que (1) y (2) sean verdaderos, pero (3) no lo es. Esto solo quiere decir que el argumento es válido.
Ahora, considere el siguiente argumento:
- Si Alex es un tigre, entonces Alex es un animal.
- Alex no es un tigre.
Alex no es un animal.
Hay situaciones en las que el argumento funciona perfectamente bien. Por ejemplo, supongamos que Alex no es un tigre sino que es, de hecho, una mesa. En este caso, Alex tampoco sería un animal. Y así, las frases (4), (5), y (6) serían ciertas. Pero no siempre es así, pues podemos imaginar una situación en la que las premisas sean ciertas pero la conclusión falsa, como donde Alex no es un tigre sino que es, de hecho, un perro. Así, imaginando la situación que acabamos de describir, habríamos producido un contraejemplo: en esta situación, (6) sería falso, y de ahí no sería consecuencia de (4) y (5). El argumento no es válido.
Que el argumento es inválido también puede ser verificado por el método de tablas de verdad. Porque podemos encontrar una situación en la que (4) y (5) son a la vez verdaderas y sin embargo (6) falsas. Es decir, en la tabla de verdad, si representamos (4) como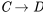 , (5) como
, (5) como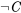 , y (6) como
, y (6) como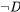 , habrá al menos una fila en la que las premisas sean verdaderas y la conclusión falsa (¿qué fila es esa?) :
, habrá al menos una fila en la que las premisas sean verdaderas y la conclusión falsa (¿qué fila es esa?) :
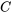 |
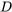 |
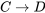 |
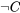 |
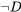 |
|---|---|---|---|---|
| T | T | T | F | F |
| T | F | F | F | T |
| F | T | T | T | F |
| F | F | T | T | T |
Dijimos que a los logísticos les preocupa la validez o invalidez de los argumentos, y propusimos el método de tablas de verdad para acometer esta tarea. Pero, ¿qué argumentos son válidos y cuáles no? Es aquí donde surge la noción de forma lógica. Supongamos que un lógico se embarca en la ridícula tarea de registrar todos y cada uno de los argumentos válidos. En este caso, seguramente registraría que (1) - (3) es válido. Ahora, supongamos que enfrenta el siguiente argumento:
- Si Alice está leyendo a Hegel, no se siente frustrada.
- Alice está frustrada.
Alice no está leyendo a Hegel.
Para ver si este argumento es válido o no, puede reescribir cada frase del argumento en su lenguaje lógico: Alice está leyendo a Hegel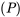 ; Alice está frustrada
; Alice está frustrada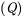 ; y, si Alice está leyendo a Hegel, entonces Alice no se frustra)
; y, si Alice está leyendo a Hegel, entonces Alice no se frustra)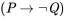 . Luego puede diseñar una tabla de verdad adecuada, y verificar si hay alguna fila o situación en la que las premisas sean verdaderas y la conclusión falsa. Ya que no hay tal fila (¿por qué?) , anunciará correctamente que el argumento es válido.
. Luego puede diseñar una tabla de verdad adecuada, y verificar si hay alguna fila o situación en la que las premisas sean verdaderas y la conclusión falsa. Ya que no hay tal fila (¿por qué?) , anunciará correctamente que el argumento es válido.
Pero es obvio que para verificar la validez de (7) - (9), nuestro lógico no necesitó acudir a este esfuerzo. Baste si solo señalara que los dos argumentos (1) - (3) y (7) - (9), y sus respectivas tablas de verdad, son en gran medida similares; tienen la misma forma. De hecho, su única diferencia es que en la primera se han utilizado las letras A y B, y en la segunda se han sustituido por P y Q, respectivamente. Los conectivos lógicos y no
y no han cambiado.
han cambiado.
Para ver el punto, traduzcamos cada argumento al lenguaje de la lógica proposicional que introdujimos anteriormente:
Los dos argumentos tienen algo en común. Digamos que lo que tienen en común es su forma lógica. Como puede ver, las conectivas lógicas de los argumentos no han cambiado. Dado que los dos argumentos tienen la misma forma, si uno es válido, entonces el otro debe ser válido, también. De manera más general, todos los argumentos de esta misma forma son válidos. La noticia liberadora es que nuestro lógico no necesita embarcarse en la exasperante tarea de verificar la validez de todos y cada uno de los argumentos por separado. Porque si ya sabe que un argumento dado es válido, y si también puede demostrar que otro argumento tiene la misma forma que el primero, entonces puede estar segura de que el segundo argumento es válido sin tener que diseñar su tabla de verdad.
Dijimos que un argumento es válido si no es posible que las premisas sean verdaderas y la conclusión falsa. Ahora bien, podemos decir que todo argumento que comparte su forma con un argumento válido también es válido, y en consecuencia, todo argumento que comparte su forma con un argumento inválido también es inválido. [1] Es en este sentido que la idea de forma lógica puede ser utilizada para establecer la (in) validez de los argumentos. Por ejemplo, supongamos que queremos verificar la validez del siguiente argumento:
- Si Alice está leyendo a Russell, entonces Alice está pensando en la lógica.
- Alice no está leyendo a Russell.
Alice no está pensando en la lógica.
En cuanto vemos que (10) - (12) tiene la misma forma que (4) - (6), que ya sabemos que es inválida, podemos estar seguros de que el primero también es inválido sin tener que construir su tabla de verdad.
Así, podemos ver que entender la noción de validez en términos de forma lógica nos permite identificar diversas falacias formales. Por ejemplo, el argumento (10) - (12) es una instancia de la falacia de negar el antecedente. Así, todo argumento que comparte su forma con (10) - (12) también es inválido.
Hay tres preguntas más que podemos hacer sobre las formas lógicas: (i) ¿Cómo podemos “extraer” la forma lógica de los argumentos que comparten? Es decir, ¿cómo podemos demostrar que diversos argumentos son instancias de una forma lógica común? ii) ¿Cuál es la naturaleza de una forma lógica? Es una forma lógica una cosa, y si es así, ¿qué clase de cosas es? (iii) ¿Cada argumento tiene una sola forma lógica? En las tres secciones siguientes, hablaremos de estas tres preguntas, respectivamente.
Extracción de formas lógicas
Consideremos, nuevamente, los argumentos (1) - (3) y (7) - (9) que parecen compartir una y la misma forma lógica. ¿Cómo podemos demostrar que tienen una forma lógica común? Primero, debemos representarlos en símbolos lógicos:
Para ver lo que estos dos argumentos tienen en común, debemos abstraer (o ignorar o dejar de lado) los contenidos específicos de sus premisas y conclusiones particulares, y con ello revelar una forma general que es común a estos argumentos. Por ejemplo, hay que ignorar si Alex es o no una rosa; lo único que importa es sustituir “Alex es una rosa” por B. En este sentido, para obtener o extraer la forma lógica de un argumento, debemos abstraernos del contenido de las premisas y de la conclusión considerándolas como meros colocadores en la forma que exhibe el argumento. Como habrás notado, no extraemos el contenido de las conectivas lógicas. Es una pregunta importante de por qué no nos alejamos de las conectivas lógicas. El pensamiento básico es que su significado constituye una parte importante de la forma lógica de un argumento, y con ello en la determinación de su (in) validez.
Para hablar de formas lógicas, usaremos las letras griegas minúsculas como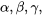 y
y . Por ejemplo, podemos representar la forma lógica que (1) - (3) y (7) - (9) comparten de la siguiente manera:
. Por ejemplo, podemos representar la forma lógica que (1) - (3) y (7) - (9) comparten de la siguiente manera:
Una analogía puede ayudar aquí: En matemáticas, pensamos en proposiciones aritméticas particulares como “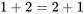 ” y “”
” y “”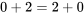 . Pero cuando queremos generalizar, utilizamos fórmulas que contienen variables, y no números específicos. Por ejemplo, “
. Pero cuando queremos generalizar, utilizamos fórmulas que contienen variables, y no números específicos. Por ejemplo, “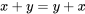 ” expresa algo general sobre el comportamiento de los números naturales. Independientemente de lo que representen los números naturales x e y, “
” expresa algo general sobre el comportamiento de los números naturales. Independientemente de lo que representen los números naturales x e y, “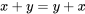 ” sigue siendo cierto. Lo mismo ocurre con las variables
” sigue siendo cierto. Lo mismo ocurre con las variables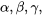 y
y , que nos permiten platicar de manera general sobre las premisas y conclusión de argumentos. Cualquiera que sea el sentido
, que nos permiten platicar de manera general sobre las premisas y conclusión de argumentos. Cualquiera que sea el sentido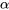 y
y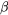 se les dé, es decir, cualesquiera que sean las proposiciones que expresen, (i) a (iii) sigue siendo válido, y así lo hacen todas sus instancias, como (1) - (3) y (7) - (9).
se les dé, es decir, cualesquiera que sean las proposiciones que expresen, (i) a (iii) sigue siendo válido, y así lo hacen todas sus instancias, como (1) - (3) y (7) - (9).
Como se mencionó anteriormente, extraer cierta forma lógica nos permite hablar, de manera general, sobre premisas y conclusiones de argumentos. No importa de qué objetos y propiedades específicos —qué tema específico importa— hablen. Y esto nos lleva, de nuevo, a nuestra preocupación inicial por el verdadero tema de la lógica:
Por lo tanto, la forma puede estudiarse independientemente de la materia, y es principalmente en virtud de su forma, ya que resulta, más que en su materia que los argumentos son válidos o inválidos. De ahí que sean las formas de argumento, más que los propios argumentos reales, lo que investiga la lógica. (Lemmon 1971, 4)
De acuerdo con esta concepción de lógica, los lógicos están en condiciones de evaluar la validez de un argumento, aunque no comprendan estrictamente el contenido de las afirmaciones dentro del argumento, ni bajo qué condiciones serían ciertas. Que las afirmaciones dentro de los argumentos sean o no ciertas, por lo tanto, no es cuestión de lógica. En cambio, lo que hace la lógica es explorar las formas lógicas de los argumentos, y con ello establecer su (in) validez.
La naturaleza de las formas lógicas
En esta y en la siguiente sección, vamos a investigar asuntos más filosóficos. En esta sección, discutiremos nuestra segunda pregunta: ¿cuál es la naturaleza de una forma lógica? La pregunta sobre la naturaleza de la forma lógica es una reminiscencia de la antigua cuestión sobre la naturaleza de los universales. Todas las rosas rojas tienen algo en común; todas comparten o instancian algo. Pero, ¿qué es esa cosa, si es una cosa en absoluto? ¿La propiedad de ser rojo es similar a un universal platónico que existe independientemente de las rosas rojas que lo instancian? ¿O es como un universal aristotélico cuya existencia depende de la existencia de las rosas particulares? Quizás, no tiene ninguna existencia en absoluto; no es más que un nombre o una etiqueta que usamos para hablar de rosas rojas. Podemos hacer exactamente las preguntas paralelas sobre las formas lógicas: ¿Qué es lo que comparten o instancian todos los argumentos válidos de la misma forma? ¿Es una entidad en el mundo, o un símbolo en el lenguaje, o una construcción mental formada y creada por nosotros?
Asumiendo que existen formas lógicas, ¿qué son? Aquí hay, en términos generales, dos líneas de pensamiento. Según la primera, las formas lógicas son esquemas, y por lo tanto, son entidades lingüísticas. Según la segunda, las formas lógicas son propiedades: son entidades extralingüísticas, afines a los universales. Son lo que los esquemas expresan o representan. (Una analogía puede ayudar aquí: La expresión “es feliz” es un predicado; es un ítem lingüístico. Pero expresa una entidad extralingüística, como la propiedad de ser feliz.)
Identificar formas lógicas con esquemas parece ser bastante intuitivo. Pero lleva a una falacia. Como señala Timothy Smiley, la falacia radica en “tratar al medio como el mensaje” (Smiley 1982, 3). Considere la forma lógica de (1) - (3):
Es posible que desee, con igual derecho, identificar la forma lógica de (1) - (3) con:
Y otro lógico puede preferir capturar su forma lógica con un conjunto distinto de variables:
¿Cuál de estos es la forma lógica de (1) - (3)? Hay muchas formas diferentes de capturar su forma lógica. ¿Cuál de ellos tiene derecho a ser calificado como la forma lógica de (1) - (3)? Esta pregunta es apremiante si las formas lógicas se toman como esquemas, y por lo tanto para ser entidades lingüísticas. Si una forma lógica es solo una cadena de símbolos, entonces varía usando un conjunto distinto de variables. No habrá manera no arbitraria de elegir uno en contraposición a cualquier otro como la forma lógica de un argumento dado. Es decir, no habrá nada que elegir entre estas entidades lingüísticamente distintas y, por lo tanto, ninguna de ellas podría identificarse con la forma lógica del argumento original.
Esto puede animarnos a identificar las formas lógicas como entidades independientes del lenguaje o invariantes del idioma. En esta visión, las formas lógicas se identifican no con esquemas, sino con lo que los esquemas expresan o representan. Son entidades mundanas, más que lingüísticas. Esta visión no sucumbe al problema anterior. Dado que, en este punto de vista, las formas lógicas son entidades mundanas, ninguno de los candidatos anteriores —es decir, (i) - (iii), (iv) - (vi) y (vii) - (ix) —es la forma lógica de (1) - (3). Más bien, cada uno de ellos expresa o representa su forma lógica.
¿Una forma lógica o muchas?
Parece entonces que estaremos en una mejor posición si asumimos que las formas lógicas son entidades mundanas. Pero esto tampoco nos deja completamente en casa y secos. Hasta el momento, hemos asumido que las formas lógicas son entidades únicas. Es decir, asumimos que argumentos como (1) - (3) y (7) - (9) tienen o ne y la misma forma lógica. Pero, ¿ese es el caso?
En general, los objetos pueden tomar muchas formas. Por ejemplo, un soneto en particular puede ser tanto Petrarchan como Miltonic, y un jarrón puede ser tanto un cuboide como un cubo. [2] También, parece que una sola oración puede tomar muchas (al menos, más de una) formas. Considerar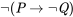 . ¿Cuál es su forma lógica? Parece que cada una de las siguientes opciones funciona perfectamente bien como respuesta a nuestra pregunta: es una negación; es una negación de un condicional; y es una negación de un condicional cuyo consecuente es una negación. [3]
. ¿Cuál es su forma lógica? Parece que cada una de las siguientes opciones funciona perfectamente bien como respuesta a nuestra pregunta: es una negación; es una negación de un condicional; y es una negación de un condicional cuyo consecuente es una negación. [3]
Ahora, supongamos que cada una de estas formas lógicas es una forma lógica de un argumento dado. En virtud de lo que cada uno de ellos es una forma lógica de un mismo argumento? Es decir, ¿qué explica el hecho de que diferentes formas lógicas son formas de un mismo argumento? ¿Qué los unifica en este sentido? Una respuesta es decir que todas estas formas tienen una forma lógica común. Pero entonces puedes hacer la misma pregunta sobre esta forma lógica común, ya que esta misma forma tiene otras formas diferentes. ¿En virtud de cuáles son estas formas lógicas de una y la misma forma? Y este proceso puede ir sin fin. Tienes una forma lógica que a su vez tiene otras formas lógicas, y así sucesivamente. Pero esto no es compatible con la tesis de que las formas lógicas son entidades únicas. [4]
Pregunta para la reflexión
Parece que no siempre podemos hablar de la forma lógica que comparten un argumento o varios argumentos. Si esta visión es correcta, ¿cuáles son sus implicaciones filosóficas? ¿Todavía podemos entender la noción de validez en términos de la noción de forma lógica?
Resumen
Este capítulo comenzó con una pregunta sobre el tema de la lógica formal: ¿qué es lo que estudia la lógica formal? Se discutió la tesis de que la lógica formal estudia la consecuencia lógica a través de la forma de argumentos. Luego explicamos la noción de validez en términos de tablas de verdad, que especifican las condiciones bajo las cuales una proposición es verdadera o falsa; por ejemplo, una proposición condicional es falsa sólo cuando su antecedente es verdadero y su consecuencia falsa; de lo contrario, es verdad. Así, como discutimos anteriormente, se pueden emplear tablas de verdad para determinar si los argumentos formulados en el lenguaje de la lógica proposicional son válidos.
Luego profundizamos en lo que significa que los argumentos tengan una forma lógica, y cómo su forma lógica impacta su (in) validez. La idea principal es que todo argumento que comparte su forma lógica con un argumento válido también es válido, y en consecuencia, todo argumento que comparte su forma lógica con un argumento inválido también es inválido. Vimos como esta comprensión de la noción de validez nos permite identificar falacias formales, como la falacia de afirmar lo consecuente. Terminamos este capítulo haciendo tres preguntas filosóficas sobre la naturaleza, existencia y singularidad de las formas lógicas.
EJERCIOS
Ejercicio Uno
Usando una tabla de verdad, mostrar que el siguiente argumento, que se conoce como la falacia de afirmar lo consecuente, no es válido:.
Ejercicio Dos
Usando una tabla de verdad, cómo es válido ese argumento siguiente, que se conoce como el silogismo hipotético:. [Pista: Tu tabla de verdad debe tener ocho filas, ya que hay tres variables proposicionales (A, B y C) que debes incluir dentro de ella.]
Ejercicio Tres
Usa las tablas de verdad ya dadas para el condicional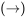 y la negación
y la negación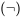 , y las dos nuevas tablas de verdad para conjunción
, y las dos nuevas tablas de verdad para conjunción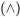 y disyunción a
y disyunción a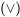 continuación, que se utilizan para expresar lógicamente usos comunes de la vernácula 'y' y 'o', respectivamente:
continuación, que se utilizan para expresar lógicamente usos comunes de la vernácula 'y' y 'o', respectivamente:
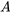 |
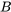 |
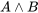 |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
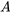 |
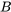 |
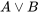 |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Evaluar si los siguientes argumentos son válidos o no válidos. En primer lugar, identificar su forma lógica, y luego usar tablas de verdad para establecer su (in) validez.
- Ahora conocemos la situación. Los Yankees o tienen que vencer a los Medias Rojas o no van a llegar a la Serie Mundial, y no van a hacer lo primero.
- Sarah solo aprobará el examen de matemáticas discretas si conoce su teoría de conjuntos. Afortunadamente, sí conoce bien la teoría de conjuntos, por lo que aprobará el examen.
- Simplemente no es el caso de que puedas ser liberal y republicano, así que o no eres republicano o no eres liberal.
- Si Dylan va a la facultad de derecho o medicina entonces estará bien financieramente. Afortunadamente, va a la escuela de derecho.
- Es más exacto decir que todo argumento que comparte su forma con un argumento inválido también es inválido dentro de esa lógica, pero no necesariamente para cada lógica. Por ejemplo, en la lógica proposicional,
- Todos los hombres son mortales
- Sócrates es un hombre
Sócrates es mortal
- Todos los hombres son inmortales
- Sócrates es un hombre
Sócrates es mortal
- P
- Q
R
- Ver Oliver (2010, 172), donde no está de acuerdo con Strawson (195, 54).
- Esta forma de poner el punto se debe a Smith (2012, 81).
- Esto es una reminiscencia del argumento aristotélico del Tercer Hombre contra la teoría de las Formas de Platón.