5: Condiciones Necesarias y Suficientes
- Page ID
- 102698
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los conceptos de condiciones necesarias y suficientes juegan un papel central y vital en la filosofía analítica. Por ejemplo, ser un varón soltero es una condición necesaria para ser soltero y ser soltero es una condición suficiente para ser un varón soltero. Que estos conceptos son vitales para la filosofía está fuera de toda duda, y es principalmente porque el relato ortodoxo de la metodología de la filosofía analítica implica la afirmación de que la filosofía pretende producir especificaciones precisas de conjuntos de condiciones necesarias y suficientes, como la afirmación de que todos los solteros son hombres solteros. Es, entonces, evidente y profundamente importante para la filosofía que tengamos una comprensión lógica adecuada de estos conceptos. En términos tanto de lógica proposicional como de primer orden los conceptos de condiciones necesarias y suficientes están íntimamente relacionados con el concepto de lo condicional (es decir, una declaración de la forma “si p, entonces q”) como deja claro el siguiente relato canónico. [1] Donde S (p, q) significa “p es una condición suficiente para q” y N (q, p) significa “q es una condición necesaria para p”,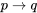 significa “si p, entonces q”, y
significa “si p, entonces q”, y significa “p y q son lógicamente equivalentes”, se supone que las siguientes dos definiciones representan estas dos ideas importantes:
significa “p y q son lógicamente equivalentes”, se supone que las siguientes dos definiciones representan estas dos ideas importantes:
\[\mathrm{S}(p, q) \equiv (p \rightarrow q)\]
\[\mathrm{N}(q, p) \equiv (p \rightarrow q)\]
En efecto, D1 y D2 pretenden ser entonces las interpretaciones lógicas estándar de nuestros conceptos de lenguaje ordinario de condiciones necesarias y suficientes enmarcadas en términos de lógica proposicional clásica. [2] Se basan en la idea de que las condiciones necesarias y suficientes pueden definirse exhaustivamente en términos de lo condicional entendido como implicación material y representado por el “→” de la lógica proposicional clásica con las siguientes condiciones familiares de verdad: [3]
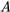 |
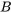 |
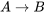 |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Por supuesto, la implicación material juega un papel importante en el razonamiento en general, particularmente con respecto a las siguientes formas inferenciales válidas en la lógica proposicional clásica, como vimos en el Capítulo 3.
1. \(A \rightarrow B\)
2. \(A\)
3. \(/ \therefore B\)
1. \(A \rightarrow B\)
2. \(\neg B\)
3. \(/ \therefore \neg A\)
Estas formas de inferencia tienen conexiones importantes con los conceptos de condiciones necesarias y suficientes, y con la forma en que razonamos utilizándolas. En el caso de afirmar el antecedente, la primera premisa puede entenderse como la afirmación de que A es suficiente para B, y la segunda premisa la afirmación de que obtiene la condición A. Entonces, de estas afirmaciones se deduce válidamente que B obtiene. En el caso de negar lo consecuente, la primera premisa puede leerse como la pretensión de que B es una condición necesaria para A y la segunda premisa como la pretensión que B no obtiene. De estas premisas se deduce válidamente que A no obtiene.
Sin embargo, las siguientes formas inferenciales que implican implicación material no son válidas en la lógica proposicional clásica:
1. \(A \rightarrow B\)
2. \(B\)
3. \(/ \therefore A\)
1. \(A \rightarrow B\)
2. \(\neg A\)
3./\(\therefore \neg B\)
Estas formas de inferencia inválidas también están relacionadas de manera importante con los conceptos de condiciones necesarias y suficientes. En el caso de afirmar lo consecuente, la primera premisa puede leerse como la afirmación de que A es una condición necesaria para B y la segunda premisa como la afirmación de que B es verdadera. Pero, a partir de estas premisas no se desprende válidamente que A también sea cierto. El hecho de que B sea necesario para A no asegura que también sea suficiente para A. En el caso de negar el antecedente, la primera premisa puede leerse como la afirmación de que A es una condición suficiente para B y la segunda premisa como la afirmación de que A no es cierta. De estas premisas no se desprende válidamente que B no es cierto, ya que alguna otra condición que basta para B podría, de hecho, obtener.
Además, cuando NS (p, q) significa “p es necesario y suficiente para q, y q es necesario y suficiente para p”, dichas condiciones conjuntamente necesarias y suficientes toman la siguiente forma: [4]
\[\mathrm{NS}(p, q) \equiv [(p \rightarrow q) \,\& \,(q \rightarrow p)]\]
Sin embargo, dado que la fórmula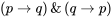 es equivalente a la fórmula
es equivalente a la fórmula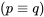 en la lógica proposicional clásica, conjuntos de tales condiciones necesarias y suficientes pueden definirse de manera más compacta en términos de equivalencia lógica de la siguiente manera:
en la lógica proposicional clásica, conjuntos de tales condiciones necesarias y suficientes pueden definirse de manera más compacta en términos de equivalencia lógica de la siguiente manera:
\[\mathrm{NS}(p, q) \equiv (p \equiv q)\]
Este concepto es solo la idea de que los valores de verdad de p y q son siempre los mismos, y la noción de equivalencia lógica tiene las siguientes condiciones de verdad:
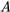 |
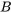 |
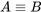 |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
Conjuntos de condiciones conjuntamente necesarias y suficientes son, entonces, solo definiciones regidas como oraciones de este tipo. Por ejemplo, resulta que ser soltero y ser un varón soltero son conjuntamente condiciones necesarias y suficientes el uno para el otro. Ahora bien, ¿por qué, específicamente, los conceptos de condiciones necesarias y suficientes, son tan entendidos, de tal trascendencia central en la filosofía analítica contemporánea?
Análisis conceptual y condiciones necesarias y suficientes
El relato central de los métodos de la filosofía analítica contemporánea se basa en la afirmación de que la metodología filosófica es un análisis conceptual impulsado por la intuición que tiene como objetivo determinar verdaderos conjuntos de condiciones necesarias y suficientes. De hecho, según un número significativo de filósofos, dicho análisis conceptual es el único método de filosofía. Para los fines que nos ocupa, este relato de los métodos de la filosofía se denominará el método filosófico estándar (SPM). Los análisis conceptuales toman la forma de especificaciones del contenido de un concepto pre-teórico (los analistas) a través de la articulación de un conjunto de condiciones necesarias y suficientes (el analysandum o analysanda), y aquí encontramos el locus de la conexión entre los conceptos de necesario y suficiente condiciones y metodología filosófica. Este relato metodológico de la filosofía se puede caracterizar más completamente de la siguiente manera:
- Los análisis conceptuales toman la forma de definiciones propuestas (es decir, conjuntos de condiciones necesarias y suficientes) de análisisda.
- La idoneidad de cualquier analysandum se puede probar contra casos concretos y/o imaginados.
- Si un análisis propuesto es adecuado o no con respecto a un caso dado puede determinarse mediante el uso de la intuición a priori, siendo la intuición a priori una facultad mental no sensorial distinta, confiable y falible. [5]
- La intuición nos permite acceder de manera confiable al conocimiento sobre conceptos.
- El método de equilibrio reflexivo es el método particular por el cual las intuiciones pueden ser utilizadas para confirmar/desconfirmar el análisis. [6]
Según los defensores de SPM, esta es esencialmente la metodología ortodoxa de la filosofía analítica, y se ha asumido que es adecuada para la solución de problemas filosóficos por parte de un número significativo de filósofos tanto practicantes como destacados a lo largo de la historia reciente de la filosofía. Por ejemplo, esta es la contienda que hizo Colin McGinn en un libro reciente. McGinn no es en lo más mínimo tentativo en su defensa general de SPM como el único método de filosofía. Con este objetivo en mente, a principios de su libro de 2012 realiza la siguiente declaración extendida sobre filosofía:
... no es una especie de indagación empírica, y no es metodológicamente comparable a las ciencias naturales (aunque es comparable a las ciencias formales). Se busca el descubrimiento de las esencias. Opera “desde el sillón”: es decir, por contemplación sin ayuda (generalmente solitaria). Sus únicos experimentos son los experimentos de pensamiento, y sus datos son posibilidades (o “intuiciones” sobre las posibilidades). Así, la filosofía busca a priori el conocimiento del ser objetivo, de la realidad no lingüística y no conceptual. Estamos investigando siendo como tal, pero lo hacemos utilizando sólo métodos a priori. (McGinn 2012, 4)
Como debe ser inmediatamente evidente, este es un respaldo claro, directo y sonoro a SPM tal como se ha entendido aquí. Para apoyar esta afirmación solo necesitamos tomar nota de sus otras afirmaciones de que “... el método adecuado para descubrir la esencia de las cosas es precisamente el análisis conceptual”, (McGinn 2012, 4) y que “la filosofía, correctamente concebida, simplemente es el análisis conceptual” (McGinn 2012, 11). En efecto, cree entonces que llegamos a tales análisis considerando casos posibles y preguntándonos si el concepto se aplica o no en esos casos, es decir, consultando nuestras “intuiciones” sobre tales casos (McGinn 2012, 5). Lo que también es importante para los fines que nos ocupa es su reconocimiento de que este relato de la metodología filosófica “fue realmente la concepción estándar para la mayor parte de la historia del sujeto, de una forma u otra” (McGinn 2012, 7). Entonces, McGinn no sólo avala a SPM como la única metodología de la filosofía contemporánea, sino que además afirma que es la metodología perdurable de indagación filosófica a lo largo de su historia. [7]
Una aclaración importante con respecto a la versión de McGinn de SPM se refiere a la naturaleza del objeto de análisis (los analistas) y, lo que es más importante, a la naturaleza del propio analysandum tal como se entiende típicamente (es decir, como definiciones de un tipo particular enmarcadas como conjuntos de condiciones necesarias y suficientes). Carl Hempel hace útilmente una distinción crucial en este sentido, que podemos usar para iluminar la visión estándar de tales definiciones:
La palabra “definición” ha llegado a ser utilizada en varios sentidos diferentes... Una definición real se concibe como una declaración de las “características esenciales” de alguna entidad, como cuando el hombre se define como un animal racional o una silla como un asiento móvil separado para una persona. Una definición nominal, por otra parte, es una convención que simplemente introduce una notación alternativa, y generalmente abreviada, para una expresión lingüística dada, a la manera de estipulación. (Hempel 1952, 2)
Además, nos dice además que algunas definiciones reales deben entenderse como análisis de significados, o como definiciones analíticas, del término en cuestión. La validación de tales afirmaciones requiere únicamente que conozcamos los significados de las expresiones constituyentes, y no es necesaria ninguna investigación empírica para determinar la exactitud del analysandum (Hempel 1952, 8).
Esto es, por supuesto, precisamente lo que McGinn tiene en mente con respecto al análisis conceptual. Es, entonces, digno de hacer el punto obvio de que el análisis conceptual es la operación de analizar conceptos a través de proponer definiciones, pero señalar que no es suficiente para captar completamente la visión. Es cierto que SPM es un método que toma como insumos nuestros conceptos, pero implica el claro reconocimiento de que las definiciones involucradas deben entenderse como análisis de significados más que como definiciones nominales o estipulativas (es decir, “diccionario”). Entonces, por ejemplo, la cuestión de si el conocimiento se justifica la verdadera creencia es solo la cuestión del análisis del concepto de conocimiento en términos de definiciones constituidas por conjuntos de condiciones necesarias y suficientes entendidas como un análisis de significados. El análisis conceptual es entonces un método para hacer algo con conceptos que ya poseemos, de donde provengan en última instancia. [8] Se trata de definir un concepto pre-teórico al ofrecer una expresión sinónima. Entonces parece ocurrir que los defensores de SPM deben creer que los conceptos tienen la forma de conjuntos de condiciones necesarias y suficientes, que tales análisis son análisis de significado, y que los análisis de nuestros conceptos preanalíticos son informativos. Los análisis típicos son, por lo tanto, tipos de descomposiciones de conceptos preanalíticos. Son verdades conceptuales con la forma de definiciones analíticas.
Entonces, para McGinn y otros pensadores afines, los analizadostienen una forma lógica muy simple, y podemos verlo a través del ejemplo del análisis del concepto de conocimiento. Donde K x es “x es conocimiento”, J x es “x está justificado”, T x es “x es verdadero” y B x es “x se cree”, el análisis estándar del conocimiento se ve así:
\[\equiv\]
Se supone que este análisis nos dice la verdadera naturaleza, o esencia, del concepto de conocimiento en términos de un conjunto finito de rasgos esenciales definitorios, con la forma lógica de un conjunto de condiciones conjuntamente necesarias y suficientes. Entonces, proporcionar tal análisis implica descomponer a los analizadores en una lista de características, exponiendo así en algún sentido importante el contenido del concepto.
Un problema con la visión ortodoxa y SPM
Muchos críticos recientes han atacado a SPM en términos de (2) - (5) desafiando la confiabilidad de la facultad de intuición. Esta es la principal línea de crítica contra SPM que ofrecen muchos defensores de lo que se llama filosofía experimental, y es una crítica interesante de la filosofía ortodoxa efectivamente. Sin embargo, algunos críticos han atacado alternativamente a SPM desafiando (1) sobre la base de la teoría de conceptos que asume; específicamente, la idea de que los conceptos pueden ser capturados adecuadamente por conjuntos de condiciones necesarias y suficientes. [9] Una versión de esta última forma de crítica es particularmente relevante para este capítulo. Esta crítica se basa en el argumento de que SPM asume erróneamente que los conceptos toman la forma de condiciones necesarias y suficientes en absoluto. Llama a esto el problema potencial de la vacuidad.
El problema potencial de la vacuidad
El problema de la vacuidad potencial surge de la siguiente manera, y se basa en los infames comentarios de Ludwig Wittgenstein sobre la teoría de conceptos asumidos en SPM. Abordó el tema de la confiabilidad de SPM en sus Investigaciones filosóficas y Los libros azules y marrones, y ahí Wittgenstein ataca la fundación del proyecto de análisis conceptual al intentar socavar (1) a través del examen de la afirmación de que los conceptos tienen la forma de conjuntos de condiciones necesarias y suficientes. [10] Primero, Wittgenstein rechazó la noción de que la mayoría de los conceptos, o incluso quizás alguno, pueden definirse precisamente a través de la especificación de conjuntos de condiciones necesarias y suficientes, y que este es un problema central en la filosofía ortodoxa. Esta importante revelación se hizo al señalar que los intentos filosóficos de análisis conceptual han fracasado sistemáticamente en la producción de los bienes. Nos dice explícitamente que,
No podemos circunscribir claramente los conceptos que utilizamos; no porque no conozcamos su definición real, sino porque no hay una “definición” real para ellos. (Wittgenstein 1958, 25)
Segundo, buscó sustituir la noción de conceptos entendidos como conjuntos de condiciones necesarias y suficientes por una teoría alternativa de conceptos. Este relato alternativo de conceptos se basa en la noción de una “relación de semejanza familiar”.
Para ver más claramente el primer punto, veamos el ejemplo favorito de Wittgenstein desde sus Investigaciones Filosóficas. Wittgenstein argumentó específicamente que el concepto de juego no puede analizarse correctamente en términos de un conjunto de condiciones necesarias y suficientes. Esto se debe a que los juegos no comparten algún conjunto de características definitorias en común. Más bien, los miembros del conjunto de juegos sólo son similares entre sí en algunos aspectos, y son estas relaciones de similitud las que constituyen la familia de juegos. Como hemos visto, SPM asume el siguiente principio:
(CON) Para cualquier concepto C, existe un conjunto de condiciones necesarias y suficientes que constituyen el contenido de C.
El ataque de Wittgenstein a SPM se monta a través de un ataque contra CON, y esta es la base fundamental del posible problema de vacío. Esencialmente, la esencia del problema es que si no hay (o incluso muy pocos) conceptos que puedan regirse correctamente como conjuntos de condiciones necesarias y suficientes, no puede haber (o muy pocos) análisis conceptuales correctos en el sentido de SPM. Entonces, la base de la crítica de Wittgenstein puede entenderse de la siguiente manera: se desprende de la consideración de ejemplos a lo largo de la historia de la filosofía que la mayoría o todos los intentos filosóficos de analizar conceptos proporcionando conjuntos de condiciones necesarias y suficientes han fracasado. Esto se debe a que, para cualquier conjunto propuesto de condiciones necesarias o suficientes destinadas a ser el correcto análisis de un concepto, existen instancias de ese concepto que no cumplen con el conjunto de condiciones definitorias propuestas.
Piense en el ejemplo favorito de Wittgenstein del concepto de un juego. El póquer y el fútbol se toman plausiblemente como juegos y así podríamos, por ejemplo, postular que algo es un juego, si y sólo si, esa actividad involucra a un ganador y un perdedor. Pero, el juego patty cake es otro caso plausible de un juego y no tiene un ganador y un perdedor. Entonces, esta definición de un juego en términos de un conjunto de condiciones necesarias y suficientes falla. Wittgenstein afirma que este ejemplo generaliza, y la presunta mejor explicación para los intentos filosóficos fallidos de articular los contenidos de los conceptos en términos de conjuntos de condiciones necesarias y suficientes es que los contenidos de los conceptos no son capturados por conjuntos de necesarios y condiciones suficientes (es decir, la negación de CON). En otras palabras, Wittgenstein sostiene que para cualquier (o, al menos la mayoría) intento (s) de especificar el contenido de los conceptos en términos de condiciones necesarias y suficientes, encontraremos contra-ejemplos.
Como reemplazo de CON, Wittgenstein introduce la noción de una clase de semejanza familiar. La idea central es que los casos que caen dentro de un concepto están relacionados entre sí no por un conjunto definitorio de condiciones necesarias y suficientes, sino por complejas condiciones de similitud superpuestas que relacionan grupos de miembros del conjunto total de casos que caen dentro del concepto. Sin embargo, ningún conjunto de condiciones tiene para todos y sólo para los miembros que exhiben ese concepto. Así, si Wittgenstein es correcto, la razón de que no existen análisis conceptuales correctos se debe a que los conceptos no pueden analizarse en términos de condiciones necesarias y suficientes. SPM es, por lo tanto, potencialmente (si no realmente) vacío.
Soluciones prospectivas al problema potencial de la vacuidad
¿Las críticas de Wittgenstein señalan la derrota del SPM, entonces? No necesariamente. Colin McGinn (2012) propone una solución al problema. Primero, observe que la crítica de Wittgenstein es una negación directa de (1). [11] McGinn responde mordiendo la bala contra Wittgenstein y argumentando que, aunque muy a menudo son difíciles de articular, los conceptos se caracterizan adecuadamente por conjuntos de condiciones necesarias y suficientes. Pace Wittgenstein, nuestro fracaso en articular ejemplos definitivos de tales análisis no es razón para suponer que no existen tales cosas. Más hábilmente, muestra cómo las críticas de Wittgenstein pueden ser refutadas efectivamente de la siguiente manera. Como hemos visto, la afirmación de Wittgenstein de que los conceptos no pueden ser capturados por conjuntos de condiciones necesarias y suficientes se supone que debe derivarse de su investigación del concepto de juego. Pero, como señala McGinn, del hecho de que es difícil producir los bienes en este (o cualquier otro) caso, no necesariamente se deduce que no existan tales análisis (McGinn 2012, 21-28).
En segundo lugar, Wittgenstein utiliza este punto en apoyo de la afirmación de que los conceptos en realidad tienen la estructura de un conjunto de relaciones de semejanza familiar entre elementos paradigmáticos y no paradigmáticos en la extensión de un concepto. Lo que McGinn muestra entonces es que la propia teoría de los conceptos de Wittgenstein en términos de semejanzas familiares presupone que los conceptos pueden ser capturados por un tipo especial de condiciones necesarias y suficientes: para cualquier concepto C, los miembros no paradigmáticos de C llevan una relación de semejanza familiar con el caso paradigmático ( s) de C. [12] Entonces, parecería darse el caso de que según Wittgenstein, algo es necesariamente un concepto, si y sólo si, se trata de un conjunto de entidades relacionadas por relaciones de semejanza familiar con uno o más casos paradigmáticos. Como tal, McGinn afirma con razón que Wittgenstein no rechaza a SPM. Más bien, en su tratamiento del concepto de juego está “favoreciendo una forma particular del mismo, una en la que el análisis toma la forma 'familia se asemeja a juegos de paradigma' (como ajedrez, tenis, etc.)” (McGinn 2012, 18-19). Sin embargo, esta respuesta no hace nada para calmar el problema de que tales especificaciones de contenidos conceptuales no pueden ser verdades plausiblemente necesarias, como suelen creer McGinn y otros defensores de SPM. Esto se debe a que las relaciones familiares de semejanza no pueden entenderse plausiblemente como verdades necesarias. En otras palabras, claramente no es el caso de que las relaciones de semejanza entre los objetos sean tales que sean verdaderas en todos los mundos posibles. [13] Este es el caso porque las semejanzas no son relaciones puramente objetivas entre objetos. Son relativos perceptores, y por lo tanto varían dependiendo de las características en las que uno se centre. Por ejemplo, un bolígrafo se asemeja a un lápiz cuando uno se enfoca en la función de escribir. Pero, una pluma y un lápiz no se parecen entre sí cuando uno se enfoca en cambio en la característica de contener tinta.
EJERCICIOS
Ejercicio Uno
Para cada par, decidir si el primer miembro del par es una condición necesaria para el segundo, una condición suficiente, o ninguna.
Ejemplo: El auto de Bob es azul/El auto de Bob es de color
Respuesta: El auto de Bob siendo azul es suficiente para que esté coloreado, ya que su ser azul asegura que esté coloreado. Sin embargo, no es una condición necesaria, ya que el auto de Bob podría ser coloreado sin ser azul, podría ser rojo, por ejemplo.
-
- Bob sacó el ocho de picas de una baraja ordinaria de naipes.
Bob sacó una carta negra de una baraja de naipes ordinarios. - Alice tiene un cuñado.
Alice no es hija única. - La hija de Alice está casada.
Alice es madre de familia. - La hija de Alice está casada.
Alice es abuela. - Algunas mujeres pagan impuestos.
Algunos contribuyentes son mujeres. - Todas las mujeres pagan impuestos.
Todos los contribuyentes son mujeres. - Ser mamífero.
Ser de sangre cálida. - Ser de sangre cálida.
- Ser mamífero.
- Bob sacó el ocho de picas de una baraja ordinaria de naipes.
Ejercicio Dos
Para cada reclamo, reescribirlo en términos de condiciones necesarias y/o suficientes.
Ejemplo: No se puede jugar al fútbol sin una pelota
Respuesta: Tener una pelota es necesario para jugar al fútbol.
- Debes pagar si quieres ingresar.
- Se necesita una cámara de nubes para observar partículas subatómicas.
- Si algo es un electrón es una partícula cargada.
- Tu auto solo es genial si es un Honda.
- Ser un triángulo solo es ser una forma de tres lados, bidimensional.
Ejercicio Tres
Pon a prueba por ti mismo la suposición filosófica tradicional de que los conceptos se definen por condiciones necesarias y suficientes. Trate de proporcionar las condiciones necesarias y suficientes para los siguientes conceptos, y luego pruebe este conjunto de condiciones con posibles contraejemplos:
- Cuchara
- Jardín
- Éxito
- Salud (mental y física)
Los posibles contraejemplos para su análisis de estos conceptos en términos de condiciones necesarias y suficientes pueden tomar la forma de:
- Casos a los que debería aplicarse el concepto, pero que no cumplan con tus condiciones necesarias y suficientes.
- Casos a los que el concepto no debe aplicarse, pero que sí cumplen con sus condiciones necesarias y suficientes.
- Como se dio anteriormente en el Capítulo 3.
- Véase, por ejemplo, Copi, Cohen y Flage (2007, 196, 446, 449) y Fisher (2001, 241).
- El concepto del condicional material introducido aquí es solo una formalización de lo que antes e informalmente llamábamos “condicionales”.
- NS (p, q) es entonces equivalente a S (p, q) & S (q, p) & N (p, q) & N (q, p).
- El conocimiento a priori es conocimiento totalmente independiente de cualquier experiencia.
- Las defensas recientes de SPM incluyen: Bealer (1996), Jackson (1998) y McGinn (2012). Para puntos de vista estrechamente relacionados, véase Braddon-Michell y Nola (2009). Véase Shaffer (próximamente) para una amplia discusión de esta opinión. El equilibrio reflexivo es el método para poner los casos intuitivamente verdaderos en conformidad con una regla o principio.
- Véase McGinn (2012, 4-11) para un resumen de ejemplos históricos significativos del uso de SPM, incluyendo algunos de los que aquí se discuten con más detalle.
- Estrictamente hablando, los análisis conceptuales también pueden implicar cierto grado de alteración en el contenido de los conceptos pre-teóricos, como suele ocurrir cuando dicho análisis implica hacer un concepto más preciso.
- Ver Moore (1968) y Wittgenstein (1953), por ejemplo. La paradoja del análisis de Moore parece mostrar que tales análisis no son informativos, y Wittgenstein afirma que los conceptos tienen la forma de semejanzas familiares, más que conjuntos de condiciones necesarias y suficientes. Véase también Brennan (2017) y Shaffer (2015) para preocupaciones adicionales sobre la naturaleza de las condiciones necesarias y suficientes.
- Véase Wittgenstein (1953), Lakoff (1987), Ramsey (1998), Rosch y Mervis (1998), y McGinn (2012, Ch. 3) para más información sobre este tema.
- La crítica de Wittgenstein también tiene una importante aplicación adicional a puntos de vista, como el de McGinn, donde las verdades conceptuales se entienden como verdades necesarias. Esto se debe a que si los conceptos no son capturados por conjuntos de condiciones necesarias y suficientes, y sólo tienen la forma de conjuntos de casos relacionados por semejanzas familiares, entonces no se entiende fácilmente cómo podrían ser necesariamente definiciones verdaderas. Esto se debe simplemente a que las relaciones de parecido entre las cosas parecen ser relaciones contingentes.
- Los miembros paradigmáticos de una clase de semejanza familiar son los casos centrales obvios, mientras que los casos no paradigmáticos son casos menos centrales y obvios de esa clase. Entonces, por ejemplo, un petirrojo es un caso paradigmático de la clase de aves, mientras que un pingüino es (plausiblemente) un caso no paradigmático de un ave.
- Esta comprensión de la verdad necesaria como afirmaciones que son verdaderas en todos los mundos posibles es el concepto estándar de una verdad necesaria. Tales verdades no pueden ser falsas en ningún arreglo consistente de lo que posiblemente podría existir.


