Soluciones para ejercicios
- Page ID
- 102755
CAPÍTULO UNO
En primer lugar, explique los siguientes argumentos, parafraseando lo necesario y sólo incluyendo premisas tácitas cuando se le instruya explícitamente para hacerlo. A continuación, diagrama de los argumentos.
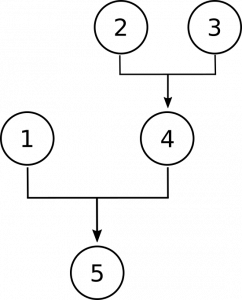
1. Los números, si existen en absoluto, deben ser objetos concretos o abstractos. Los objetos concretos —como los planetas y las personas— son capaces de interactuar con otras cosas en las relaciones de causa y efecto. Los números carecen de esta habilidad. Por lo tanto, los números son objetos abstractos. [¡Necesitarás agregar una premisa intermedia implícita aquí!]
- Los números deben ser objetos concretos o abstractos.
- Los objetos concretos son capaces de interactuar con otros objetos en relaciones de causa y efecto.
- Los números no interactúan con otros objetos en las relaciones de causa y efecto.
- Los números no son objetos concretos. [Premisa intermedia implícita]
- /* Los números son objetos abstractos.
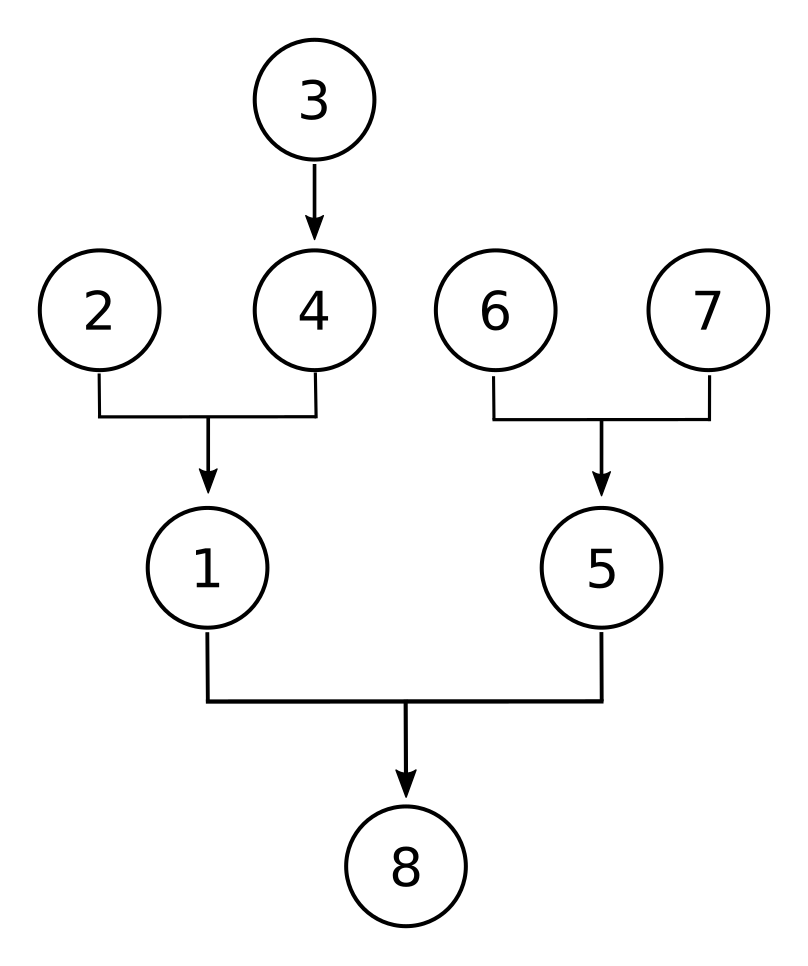
2. ¡Abolir la pena de muerte! ¿Por qué? Es inmoral. Numerosos estudios han demostrado que existe sesgo racial en su aplicación. El auge de las pruebas de ADN ha exonerado a decenas de presos condenados a muerte; ¿quién sabe cuántas personas inocentes han sido asesinadas en el pasado? La pena de muerte tampoco es práctica. La venganza es contraproducente: “Ojo por ojo deja ciego al mundo entero”, como dijo Gandhi. Además, los costos de litigar casos de pena de muerte, con sus interminables apelaciones, son enormes.
- La pena de muerte es inmoral.
- Los estudios demuestran que existe un sesgo racial en la aplicación de la pena de muerte.
- Pruebas de ADN cómo exoneró a las puntuaciones de los presos condenados a muerte.
- Presos inocentes han sido condenados a la pena de muerte
- La pena de muerte no es práctica.
- La venganza es contraproducente.
- Los costos de litigar casos de pena de muerte son enormes.
- /∙ Se debería abolir la pena de muerte.
3. Un sistema económico justo presentaría una distribución equitativa de los recursos y una ausencia de explotación. El capitalismo es un sistema económico injusto. Bajo el capitalismo, la distribución típica de la riqueza está muy sesgada a favor de los ricos. Y los trabajadores son explotados: a pesar de su papel esencial en la producción de bienes para el mercado, la mayor parte de las ganancias de las ventas de esos bienes van a los dueños de las empresas, no a sus trabajadores.
- Los sistemas económicos justos presentan una distribución equitativa de los recursos y una ausencia de explotación.
- Dentro de los sistemas capitalistas, la distribución típica de la riqueza está muy sesgada a favor de los ricos.
- Dentro de los sistemas capitalistas, los trabajadores son explotados.
- /El capitalismo es un sistema económico injusto.
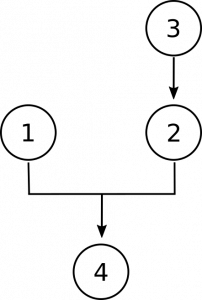
4. La mente y el cerebro no son idénticos. ¿Cómo pueden ser idénticas las cosas si tienen propiedades diferentes? Hay una propiedad que la mente y el cerebro no comparten: el cerebro es divisible, pero la mente no lo es. Como todas las cosas materiales, el cerebro se puede dividir en partes—diferentes mitades, regiones, neuronas, etc. pero la mente es una unidad. Es mi esencia pensante, en la que no puedo discernir partes separadas.
- Los objetos idénticos deben tener las mismas propiedades.
- La mente y el cerebro no tienen las mismas propiedades.
- El cerebro es divisible, mientras que la mente no lo es.
- /4-1 La mente y el cerebro no son idénticos.
5. Todo adulto sano debe participar en la fuerza laboral. Cuanta más gente trabaje, mayor será la riqueza de la nación, lo que beneficia a todos económicamente. Además, no hay reemplazo para la dignidad que los trabajadores encuentran en el trabajo. Por lo tanto, el gobierno debería emitir créditos fiscales para alentar a las personas a ingresar a la fuerza laboral. [Incluya en su explicación una premisa tácita, no enunciada explícitamente en el pasaje, sino necesaria para sustentar la conclusión. ]
- Todo adulto sano debe participar en la fuerza laboral.
- Cuanta más gente trabaje, mayor será la riqueza de la nación.
- El trabajo proporciona dignidad insustituible a las personas.
- Algunos individuos no podrán trabajar sin créditos fiscales. [Premisa intermedia implícita]
- /⟩ El gobierno debe emitir créditos fiscales para incentivar a la gente a trabajar.
CAPÍTULO DOS
Ejercicio Uno
Para cada argumento decidir si es deductivo, inductivo o abductivo. Si contiene más de un tipo de inferencia, indique cuál.
1.
- Pollos de mi granja han desaparecido.
- Mi granja está en el campo británico.
- /Hay zorros matando a mis gallinas.
Se trata de un argumento abductivo porque se trata de explicar algunos fenómenos conocidos, a saber, la desaparición de los pollos, al inferir una hipótesis a partir de toda la información que el individuo tiene a su disposición: que los zorros mataron a los pollos.
2.
- Todos los flamencos son pájaros rosados.
- Todos los flamencos son criaturas que respiran fuego.
- /⟩ Algunas aves rosadas son criaturas que respiran fuego.
Este es un argumento deductivo porque se trata de demostrar que es imposible concluir “Algunos pájaros rosados son criaturas que respiran fuego” desde las instalaciones “Todos los flamencos son pájaros rosados” y “Todos los flamencos son criaturas que respiran fuego”.
3.
- Todos los viernes en lo que va del año la cafetería ha servido pescado y patatas fritas.
- Si la cafetería sirve pescado y papas fritas y quiero pescado y papas fritas entonces debería traer £4.
- Si la cafetería no sirve pescado y papas fritas entonces no debería traer £4.
- Siempre quiero pescado y patatas fritas.
- /Debería traer 4£ el próximo viernes.
Este argumento tiene componentes tanto inductivos como deductivos. Para inferir deductivamente que debo traer 4£ el próximo viernes, en conjunto con el segundo y cuarto local, necesitamos saber que todos los viernes la cafetería sirve pescado y papas fritas. No obstante, en la actualidad no lo sabemos. Sólo sabemos que todos los viernes en lo que va del año la cafetería ha servido pescado y patatas fritas. Entonces, necesitamos hacer una inferencia inductiva (es decir, una inferencia de instancias observadas a instancias aún no observadas) desde la primera premisa antes de poder deducir la conclusión usando las otras premisas. Entonces, hecho completamente explícito el argumento se vería así:
- Todos los viernes en lo que va del año la cafetería ha servido pescado y patatas fritas.
- La cafetería sirve pescado y papas fritas todos los viernes (desde la primera premisa por inducción).
- Si la cafetería sirve pescado y papas fritas y quiero pescado y papas fritas entonces debería traer £4.
- Si la cafetería no sirve pescado y papas fritas entonces no debería traer £4.
- Siempre quiero pescado y patatas fritas.
- /Debería traer 4£ el próximo viernes.
Tenga en cuenta que la premisa tres en realidad no es necesaria en el argumento, pero esto no es un problema. Muchos argumentos tienen contenido superfluo.
4.
- Si Bob Dylan o Italo Calvino fueran galardonados con el Premio Nobel de Literatura, entonces las elecciones que hiciera la Academia Sueca serían respetables.
- Las elecciones que toma la Academia Sueca no son respetables.
- /⟩ Ni Bob Dylan ni Italo Calvino han sido galardonados con el Premio Nobel de Literatura.
Esto también es un argumento deductivo, ya que se trata de demostrar que es imposible que la conclusión sea falsa si las premisas son ambas verdaderas. También es un argumento válido, y es de la forma:
- Si A entonces B
- No B
- /alisco No A
que se conoce como Modus Tollens.
5.
- En todos los juegos que han disputado los Medias Rojas de Boston en lo que va de la temporada han sido mejores que su oposición.
- Si un equipo juega mejor que su oposición en todos sus juegos entonces ganará la Serie Mundial.
- /4-1 Los Medias Rojas de Boston ganarán la liguilla.
Este argumento tiene componentes tanto inductivos como deductivos. Usar la premisa 2 para inferir deductivamente la conclusión requiere que sepamos que los Medias Rojas de Boston han jugado mejor que todos sus oponentes, sin embargo, esta no es la premisa que uno nos dice. Entonces, para derivar la afirmación de que “Los Medias Rojas de Boston jugarán mejor que todos sus oponentes este año” necesitamos hacer una inferencia inductiva desde la premisa uno (es decir, una inferencia de instancias observadas a instancias aún no observadas). Entonces, hecho completamente explícito el argumento se vería así:
- En todos los juegos que han disputado los Medias Rojas de Boston en lo que va de la temporada han sido mejores que su oposición.
- Los Medias Rojas de Boston serán mejores que toda su oposición este año (desde primera premisa por inducción)
- Si un equipo juega mejor que su oposición en todos sus juegos entonces ganará la Serie Mundial.
- /4-1 Los Medias Rojas de Boston ganarán la liguilla.
6.
- Hay luces encendidas en la habitación delantera y hay ruidos que vienen de arriba.
- Si hay ruidos que vienen de arriba entonces Emma está en la casa.
- /alisco Emma está en la casa
Se trata de un argumento deductivo, ya que se trata de demostrar que es imposible que la conclusión sea falsa si las premisas son ambas verdaderas. También es un argumento válido, y es de la forma:
- A y B
- Si B entonces C
- /C
Esta forma de argumentación se conoce como Modus Ponens.
Ejercicio Dos
Dar ejemplos de argumentos que tienen cada una de las siguientes propiedades:
1. Sonido
Aquí quiere proporcionar un argumento que sea válido y que tenga realmente verdaderas premisas. Aquí hay un ejemplo:
- Todos los mamíferos son animales
- Los osos son mamíferos
- /alisco Los osos son animales
2. Válido, y tiene al menos una premisa falsa y una conclusión falsa
Aquí es necesario proporcionar un argumento cuya conclusión debe ser cierta si todas las premisas son verdaderas, pero que en realidad al menos una de las premisas es falsa y la conclusión es falsa. Aquí hay un ejemplo:
- Todos los peces son mamíferos
- Las pirañas son peces
- /alisco Las pirañas son mamíferos
3. Válido, y tiene al menos una premisa falsa y una conclusión verdadera
Aquí hay que aportar un argumento cuya conclusión debe ser cierta si todas las premisas son verdaderas, pero que en realidad al menos una de las premisas es falsa y la conclusión es verdadera. Aquí hay un ejemplo:
- Todas las aves pueden volar
- Las gaviotas son aves
- /alisco Las gaviotas pueden volar
4. No válido, y tiene al menos una premisa falsa y una conclusión falsa
Aquí es necesario proporcionar un argumento cuya conclusión pueda ser falsa aunque todas las premisas sean verdaderas, y también que en realidad al menos una de las premisas y la conclusión sea falsa. Aquí hay un ejemplo:
- Todas las aves pueden volar
- Las gaviotas son aves
- /alisco Las pirañas pueden volar
5. No válido, y tiene al menos una premisa falsa y una conclusión verdadera
Aquí es necesario proporcionar un argumento cuya conclusión pueda ser falsa aunque todas las premisas sean verdaderas, y también que en realidad al menos una de las premisas es falsa pero la conclusión es verdadera. Aquí hay un ejemplo:
- Todas las aves pueden volar
- Las gaviotas son aves
- /alisco Las pirañas pueden nadar
6. No válido, y tiene verdaderas premisas y una conclusión verdadera
Aquí es necesario proporcionar un argumento cuya conclusión pueda ser falsa aunque todas las premisas sean verdaderas, y también que en realidad las premisas y la conclusión sean verdaderas. Aquí hay un ejemplo:
- Todos los mamíferos son animales
- Los osos son mamíferos
- /alisco Las pirañas pueden nadar
7. No válido, y tiene verdaderas premisas y una conclusión falsa
Aquí es necesario proporcionar un argumento cuya conclusión pueda ser falsa aunque todas las premisas sean verdaderas, y también que en realidad las premisas son verdaderas pero la conclusión es falsa. Aquí hay un ejemplo:
- Todos los mamíferos son animales
- Los osos son mamíferos
- /alisco Las pirañas pueden volar
8. Fuerte, pero inválido [Pista: Piense en argumentos inductivos.]
Aquí hay que aportar un argumento fuerte, es decir, un argumento cuyas premisas sustentan su conclusión, la cual no tiene validez deductiva. La forma más fácil de hacer esto es proporcionar un argumento inductivamente fuerte:
- El Sol ha salido todos los días durante los últimos dos mil años
- /∙ Mañana saldrá el Sol
CAPÍTULO TRES
Ejercicio Uno
Usando una tabla de verdad, muestran que el siguiente argumento, que se conoce como la falacia de afirmar lo consecuente, no es válido: A→BA→B, BB; /A/A.
| A | B | A → B | B | A |
|---|---|---|---|---|
| T | T | T | T | T |
| T | F | F | F | T |
| F | T | T | T | F |
| F | F | T | F | F |
La tabla de verdad anterior muestra que el argumento es inválido, porque hay una circunstancia en la que ambas premisas son verdaderas y la conclusión es falsa (proporcionada por la tercera fila de la tabla de verdad).
Ejercicio Dos
Usando una tabla de verdad, cómo ese argumento siguiente, que se conoce como el silogismo hipotético, es válido: A → B, B → C;/⟩ A → C. [Pista: Tu la tabla de verdad debe tener ocho filas, ya que hay tres variables proposicionales —una, B y C— que debe incluir dentro de ella.]
| A | B | C | A → B | B → C | A → C |
|---|---|---|---|---|---|
| T | T | T | T | T | T |
| T | T | F | T | F | F |
| T | F | T | F | T | T |
| T | F | F | F | T | F |
| F | T | T | T | T | T |
| F | T | F | T | F | T |
| F | F | T | T | T | T |
| F | F | F | T | T | T |
La tabla de verdad anterior muestra que el argumento es válido, ya que no hay circunstancias (filas en la tabla de verdad) en las que ambas premisas sean verdaderas y la conclusión sea falsa.
Ejercicio Tres
Evaluar si los siguientes argumentos son válidos o no válidos. Primero, identificar su forma lógica, y luego usar tablas de verdad para establecer su (in) validez.
1. Ahora conocemos la situación. Los Yankees o tienen que vencer a los Medias Rojas o no van a llegar a la Serie Mundial, y no van a hacer lo primero.
- Los Yankees tienen que vencer a los Medias Rojas o los Yankees no llegarán a la Serie Mundial
- Los Yankees no ganarán a los Medias Rojas
- //⟩ Los Yankees no llegarán a la Serie Mundial
A = Los Yankees tienen que vencer a los Medias Rojas
B = Los Yankees llegarán a la Serie Mundial
- A alisco ¬ B
- ¬ A
- /¬ B
| A | B | A alisco ¬ B | ¬ A | ¬ B |
|---|---|---|---|---|
| T | T | T | F | F |
| T | F | T | F | T |
| F | T | F | T | F |
| F | F | T | T | T |
La tabla de verdad anterior muestra que el argumento es válido, ya que la única circunstancia en la que ambas premisas son verdaderas (fila cuatro de la tabla de verdad) es también una circunstancia en la que la conclusión es verdadera. Esta forma de argumentación se conoce como el silogismo disyuntivo.
2. Sarah solo aprobará el examen de matemáticas discretas si conoce su teoría de conjuntos. Afortunadamente, sí conoce bien la teoría de conjuntos, por lo que aprobará el examen.
- Si Sarah pasa su examen de matemáticas discretas, entonces conoce la teoría de conjuntos
- Sarah conoce la teoría de conjuntos
- /⟩ Sarah aprobará su examen discreto de matemáticas
A = Sarah aprobará su examen discreto de matemáticas
B = Sarah conoce la teoría de conjuntos
- A → B
- B
- /A
| A | B | A → B | B | A |
|---|---|---|---|---|
| T | T | T | T | T |
| T | F | F | F | T |
| F | T | T | T | F |
| F | F | T | F | F |
La tabla de verdad anterior muestra que el argumento es inválido, porque existe una circunstancia en la que ambas premisas son verdaderas y la conclusión es falsa (proporcionada por la tercera fila de la tabla de verdad). Esta es otra instancia de la falacia formal conocida como afirmar lo consecuente.
3. Simplemente no es el caso de que puedas ser liberal y republicano, así que o no eres republicano o no eres liberal.
- No se puede ser tanto liberal como republicano
- /⟩ O no eres republicano o no eres liberal
A = Eres un liberal
B = Eres republicano
- ¬ (A B)
- /⟩ ¬ B alisco ¬ A
| A | B | ¬ (A B) | ¬ B alisco ¬ A |
|---|---|---|---|
| T | T | F | F |
| T | F | T | T |
| F | T | T | T |
| F | F | T | T |
La tabla de verdad anterior muestra que el argumento es válido, ya que toda circunstancia en la que la premisa es verdadera es también aquella en la que la conclusión es verdadera. Este argumento es una instancia de una de las leyes de DeMorgan, que afirma que las proposiciones de la forma ¬ (AB) ¬ (AB) son equivalentes a las de la forma ¬A¬B¬A¬B ¿Cómo crees que mostramos la verdad de esta ley? [Pista: Ya hemos logrado uno de los dos pasos requeridos]
4. Si Dylan va a la facultad de derecho o medicina entonces estará bien financieramente. Afortunadamente, va a la escuela de derecho.
- Si Dylan va a la facultad de derecho o Dylan va a la escuela de medicina, estará bien financieramente
- Dylan va a la facultad de derecho
- /Dylan estará bien financieramente
A = Dylan va a la facultad de derecho
B = Dylan va a la escuela de medicina
C = Dylan estará bien financieramente
- (A) → C
- A
- /C
| A | B | C | (A) → C | A | C |
|---|---|---|---|---|---|
| T | T | T | T | T | T |
| T | T | F | F | T | F |
| T | F | T | T | T | T |
| T | F | F | F | T | F |
| F | T | T | T | F | T |
| F | T | F | F | F | F |
| F | F | T | T | F | T |
| F | F | F | T | F | F |
La tabla de verdad anterior muestra que el argumento es válido, ya que en las dos únicas circunstancias en las que ambas premisas son verdaderas (la primera y tercera fila de la tabla de verdad) la conclusión también es verdadera. Este argumento es una instancia de afirmar el antecedente, también conocido como modus ponens, pero en el que el antecedente es una disyunción más que una proposición singular.
CAPÍTULO CUATRO
Ejercicio Uno
Para cada enunciado identificar la falacia informal.
1. No está mal que los periódicos transmitan rumores sobre escándalos sexuales. Los periódicos tienen el deber de imprimir historias que sean de interés público, y el público claramente tiene un gran interés por los rumores sobre escándalos sexuales ya que cuando los periódicos imprimen tales historias, su circulación aumenta.
Este argumento trata sobre una equívoca del significado de “interés público”.
El argumento puede parecer plausible porque en primera instancia de “interés público”, esto significa “en el bien público”, pero en la segunda instancia, “gran interés” solo significa, “al público le parece interesante”. Dado que en el bien público y el público lo encuentran interesante no significan lo mismo, el argumento descansa en un equívoco.
2. El libre comercio será bueno para este país. El motivo es claramente claro. ¿No es obvio que las relaciones comerciales irrestrictas otorgarán a todos los sectores de esta nación los beneficios que resultan cuando hay un flujo sin trabas de bienes entre países?
Este argumento plantea la pregunta, pues simplemente presupone que el libre comercio será bueno para el país al reafirmar la conclusión en términos más complicados.
3. Por supuesto que el partido en el poder se opone a plazos más cortos, eso es solo porque quieren permanecer más tiempo en el poder.
Se trata de un argumento ad hominem, en el sentido de que intenta socavar el argumento (u opinión) del partido político puramente en virtud de sus motivaciones, y no comprometiéndose activamente con el argumento.
4. Una alumna mía me dijo que soy su profesora favorita, y sé que está diciendo la verdad, porque ninguna alumna le mentiría a su profesor favorito.
Este argumento plantea la pregunta. El argumento concluye que un estudiante cree que el profesor es su favorito, pero se basa en este mismo hecho para apelar a “ningún estudiante le mentiría a su profesor favorito” para establecer la conclusión.
5. Todo aquel que intente violar una ley, aunque falle el intento, debe ser castigado. Las personas que intentan volar están tratando de violar la ley de la gravedad, por lo que deben ser castigadas.
Este argumento trata sobre una equívoca del significado de “ley”. En primera instancia, en “violar una ley”, estamos destinados a interpretar esto como “derecho jurídico”, mientras que en la segunda instancia, “las personas que intentan volar están tratando de violar la ley de la gravedad”, lo que obviamente se entiende es una ley de la naturaleza, y no una ley legal.
6. Hay más budistas que seguidores de cualquier otra religión, por lo que debe haber algo de verdad en el budismo.
Este es un simple atractivo a la popularidad.
CAPÍTULO CINCO
Ejercicio Uno
Para cada par, decidir si el primer miembro del par es una condición necesaria para el segundo, una condición suficiente, o ninguna.
1.
Bob sacó el ocho de picas de una baraja ordinaria de naipes.
Bob sacó una carta negra de una baraja de naipes ordinarios.
Como las cartas de Espadas son negras, pero no las únicas cartas negras, Bob dibujar una Spade es suficiente pero no necesario para que él saque una carta negra.
2.
Alice tiene un cuñado.
Alice no es hija única.
El hecho de que Alice tenga un cuñado no es suficiente ni necesario para que Alice no sea hija única. No es suficiente porque Alice podría tener un cuñado en virtud de que su cónyuge tuviera un hermano. Adicionalmente, Alice podría tener un hermano que no esté casado con un hombre. Por lo tanto, el hecho de que Alice tenga un cuñado no es necesario para que no sea hija única.
3.
La hija de Alice está casada.
Alice es madre de familia.
El hecho de que la hija de Alice esté casada es suficiente para que Alice sea madre, ya que asegura su verdad. No obstante, no es necesario que sea madre de familia. Ella podría, por ejemplo, tener sólo hijos, o hijas solteras.
4.
La hija de Alice está casada.
Alice es abuela.
El hecho de que la hija de Alice esté casada no es necesario ni suficiente para que Alice sea abuela. No es necesario porque Alice podría ser una abuela con solo hijos, o con hijas que no están casadas. No es suficiente porque la hija de Alice podría casarse sin hijos.
5.
Algunas mujeres pagan impuestos.
Algunos contribuyentes son mujeres.
Algunas mujeres que pagan impuestos es a la vez necesario y suficiente para que algunos contribuyentes sean mujeres, ya que los dos reclamos son sinónimos.
6.
Todas las mujeres pagan impuestos.
Todos los contribuyentes son mujeres.
Todas las mujeres que pagan impuestos no es necesario ni suficiente para que todos los contribuyentes sean mujeres. No es necesario porque puede ser que mientras solo algunas mujeres paguen impuestos, ninguna no mujer lo haga, y no sea suficiente porque aunque todas las mujeres paguen impuestos, algunas no mujeres también pueden pagar impuestos.
7.
Ser un mamífero
Ser de sangre caliente
Ser mamífero es suficiente para ser de sangre caliente, ya que ser mamífero asegura ser de sangre caliente. Sin embargo, no es necesario, ya que uno puede ser de sangre caliente y un no mamífero, como un ave.
8.
Ser de sangre caliente
Ser un mamífero
Ser de sangre caliente es necesario para ser un mamífero, ya que ser mamífero requiere ser de sangre caliente. No obstante, no es suficiente, ya que además de ser de sangre caliente también se deben poseer ciertas otras características, como poseer cabello y dar a luz a vivir joven.
Ejercicio Dos
Para cada reclamo, reescribirlo en términos de condiciones necesarias y/o suficientes.
1. Debes pagar si quieres ingresar.
El pago es necesario para la entrada.
2. Se necesita una cámara de nubes para observar partículas subatómicas.
Es necesaria una cámara de nubes para observar partículas subatómicas.
3. Si algo es un electrón es una partícula cargada.
Ser un electrón es suficiente para una partícula cargada.
4. Tu auto solo es genial si es un Honda.
El hecho de que tu auto sea un Honda es necesario para que sea genial.
5. Ser un triángulo solo es ser una forma bidimensional de tres lados.
Ser un triángulo es necesario y suficiente para ser una forma bidimensional de tres lados.