2.11: Las pruebas y las ocho formas válidas de inferencia
- Page ID
- 101175
Si bien las tablas de verdad son nuestro único método formal para decidir si un argumento es válido o inválido en la lógica proposicional, existe otro método formal para probar que un argumento es válido: el método de prueba. Aunque no se puede construir una prueba para demostrar que un argumento no es válido, puede construir pruebas para demostrar que un argumento es válido. La razón por la que las pruebas son útiles, es que nos permiten demostrar que ciertos argumentos son válidos de manera mucho más eficiente que las tablas de verdad. Por ejemplo, considere el siguiente argumento:
1. (R v S) (T K)
2. ~K
3. R v S /~T
(Nota: en esta sección estaré escribiendo la conclusión del argumento a la derecha de la última premisa—en este caso premisa 3. Como antes, la conclusión que estamos tratando de derivar se denota con el signo “por lo tanto”, “”.) Podríamos intentar probar que este argumento es válido con una tabla de verdad, pero la tabla de verdad tendría 16 filas de largo porque hay cuatro proposiciones atómicas diferentes que ocurren en este argumento, R, S, T y K. Si hubiera 5 o 6 proposiciones atómicas diferentes, ¡la tabla de la verdad tendría 32 o 64 líneas de largo! No obstante, como veremos pronto, también podríamos probar que este argumento es válido con sólo dos líneas adicionales. Esa parece una forma mucho más eficiente de establecer que este argumento es válido. Haremos esto un poco más tarde, después de haber introducido las 8 formas válidas de inferencia que necesitará para hacer pruebas. Cada línea de la prueba se justificará citando una de estas reglas, siendo la última línea de la prueba la conclusión que estamos tratando de establecer en última instancia. Voy a introducir las 8 formas válidas de inferencia en grupos, comenzando por las reglas que utilizan la herradura y la negación.
La primera de las 8 formas de inferencia es “modus ponens” que es latino para “manera que afirma”. Modus ponens tiene la siguiente forma:
1. p q
2. p
3.
Lo que dice esta forma, en palabras, es que si hemos hecho valer una declaración condicional (p q) y también hemos hecho valer el antecedente de esa declaración condicional (p), entonces tenemos derecho a inferir lo consecuente de esa declaración condicional (q). Por ejemplo, si afirmaba el condicional, “si está lloviendo, entonces el suelo está mojado” y también afirmé “está lloviendo” (el antecedente de ese condicional) entonces yo (o cualquier otra persona, para el caso) tengo derecho a hacer valer lo consecuente del condicional, “el suelo está mojado”.
Al igual que con cualquier forma válida de inferencia en esta sección, podemos probar que modus ponens es válido construyendo una tabla de verdad. Como ve en la tabla de verdad a continuación, esta forma de argumento pasa la prueba de validez de la tabla de verdad (ya que no hay fila de la tabla de verdad en la que todas las premisas son verdaderas y sin embargo la conclusión es falsa).
| p | q | p q | p | q |
| T | T | T | T | T |
| T | F | F | T | F |
| F | T | T | F | T |
| F | F | T | F | F |
Por lo tanto, cualquier argumento que tenga esta misma forma es válido. Por ejemplo, el siguiente argumento también tiene esta misma forma (modus ponens):
1. (A ⋅ B) C
2. (A ⋅ B)
3.
En este argumento podemos afirmar C según la regla, modus ponens. Esto es así a pesar de que el antecedente del condicional es complejo en sí mismo (es decir, es una conjunción). Eso no importa. La primera premisa sigue siendo una declaración condicional (ya que la herradura es el operador principal) y la segunda premisa es el antecedente de esa declaración condicional. El modus ponens regla dice que si tenemos tanto, tenemos derecho a inferir lo consecuente de lo condicional.
En realidad podemos usar modus ponens en el primer argumento de esta sección:
1. (R v S) (T K)
2. ~K
3. R v S /~T
4. T K Modus ponens, líneas 1, 3
Lo que he hecho aquí es que he escrito la forma válida de inferencia (o regla) que justifica la línea que estoy derivando, así como las líneas a las que se aplica esa regla, a la derecha de la nueva línea de la prueba que estoy derivando. Aquí he derivado “T K” de las líneas 1 y 3 del argumento por modus ponens. Observe que la línea 1 es una sentencia condicional y la línea 3 es el antecedente de esa declaración condicional. Esta prueba aún no está terminada, ya que aún no hemos derivado la conclusión que estamos tratando de derivar, es decir, “~T”. Necesitamos una regla diferente para derivar eso, que vamos a introducir a continuación.
La siguiente forma de inferencia se llama “modus tollens”, que es latino para “la forma que niega”. Modus tollens tiene la siguiente forma:
1. p q
2. ~q
3. ~p
Lo que dice esta forma, en palabras, es que si hemos hecho valer una declaración condicional (p q) y también hemos afirmado el consecuente negado de ese condicional (~q), entonces tenemos derecho a inferir el antecedente negado de esa declaración condicional (~p). Por ejemplo, si afirmaba el condicional, “si está lloviendo, entonces el suelo está mojado” y también aseveré “el suelo no está mojado” (el consecuente negado de ese condicional) entonces tengo derecho a hacer valer el antecedente negado del condicional, “no está lloviendo”. Es importante ver que cualquier argumento que tenga esta misma forma es un argumento válido. Por ejemplo, el siguiente argumento es también un argumento con esta misma forma:
1. C (E v F)
2. ~ (E v F)
3. ~C
En este argumento podemos afirmar ~C según la regla, modus tollens. Esto es así a pesar de que lo consecuente de lo condicional es en sí mismo complejo (es decir, es una disyunción). Eso no importa. La primera premisa sigue siendo una declaración condicional (ya que la herradura es el operador principal) y la segunda premisa es la consecuencia negada de esa declaración condicional. La regla modus tollens dice que si tenemos tanto, tenemos derecho a inferir el antecedente negado de lo condicional.
Podemos usar modus tollens para completar la prueba que iniciamos anteriormente:
1. (R v S) (T K)
2. ~K
3. R v S /~T
4. T K Modus ponens, líneas 1, 3
5. ~T Modus tollens, líneas 2, 4
Observe que la última línea de la prueba es la conclusión que se supone que debemos derivar y que cada afirmación que he derivado (es decir, las líneas 4 y 5) tiene una regla a la derecha. Esa regla citada es la que justifica la afirmación que se está derivando y las líneas citadas son las líneas anteriores de la prueba donde podemos ver que la regla aplica. Esto es lo que se llama una prueba. Una prueba es una serie de declaraciones, comenzando por las premisas y terminando con la conclusión, donde cada declaración adicional después de las premisas se deriva de alguna línea (s) anterior (s) de la prueba utilizando una de las formas válidas de inferencia. Practicaremos esto un poco más en el ejercicio al final de esta sección.
La siguiente forma de inferencia se llama “silogismo hipotético”. Esto es lo que los filósofos antiguos llamaban “el argumento de la cadena” y debería ser obvio por qué en un momento. Aquí está la forma de la regla:
1. p q
2. q r
3. p r
Como puede ver, la conclusión de este argumento vincula p y r juntos en una declaración condicional. Podríamos seguir agregando condicionales como “r s” y “s t” y las inferencias serían igual de válidas. Y si los alineamos todos como tengo a continuación, se puede ver por qué los filósofos antiguos se referían a esta forma de argumento válido como un “argumento en cadena”:
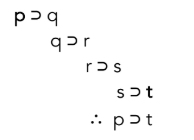
Observe cómo el consecuente de cada sentencia condicional precedente se vincula con el antecedente de la siguiente declaración condicional de tal manera que se cree una cadena. La cadena podría ser tan larga como nos haya gustado, pero la regla que vamos a citar en nuestras pruebas sólo conecta dos declaraciones condicionales diferentes juntas. Como antes, es importante darse cuenta de que cualquier argumento con esta misma forma es un argumento válido. Por ejemplo,
1. (A v B) ~D
2. ~D C
3. (A v B) C
Observe que lo consecuente de la primera premisa y el antecedente de la segunda premisa son exactamente el mismo término, “~D”. Eso es lo que nos permite “vincular” el antecedente de la primera premisa y lo consecuente de la segunda premisa juntos en una “cadena” para inferir la conclusión. Ser capaz de reconocer las formas de estas inferencias es una habilidad importante en la que tendrás que adquirir dominio para poder hacer pruebas.
Las siguientes cuatro formas de inferencia que introduciremos utilizan conjunción, disyunción y negación de diferentes maneras. Comenzaremos con la regla llamada “simplificación”, que tiene la siguiente forma:
1. p ⋅ q
2. -02 p
Lo que dice esta regla, en palabras, es que si hemos hecho valer una conjunción entonces tenemos derecho a inferir cualquiera de las conjunciones. Esta es la regla que introduje en la primera sección de este capítulo. Se trata de una regla bastante “obvia” —tan obvia, de hecho, que incluso podríamos preguntarnos por qué tenemos que expresarla. Sin embargo, toda forma de inferencia que introduzcamos en esta sección debe ser obvia, es decir, el punto de llamarlas formas básicas de inferencia. Son algunas de las formas más simples de inferencia, cuya validez debe ser transparentemente obvia. La idea de una prueba es que aunque la inferencia que se hace en el argumento no es obvia, podemos romper esa inferencia en escalones, cada uno de los cuales es obvio. Así, las inferencias obvias justifican en última instancia la inferencia no obvia que se hace en el argumento. Esas inferencias obvias funcionan así como reglas que utilizamos para justificar cada paso de la prueba. La simplificación es un excelente ejemplo de una de las reglas más obvias.
Como antes, es importante darse cuenta de que cualquier inferencia que tenga la misma forma que la simplificación es una inferencia válida. Por ejemplo,
1. (A v B) ⋅ ~ (C ⋅ D)
2. (A v B)
es una inferencia válida porque tiene la misma forma que la simplificación. Es decir, la línea 1 es una conjunción (ya que el punto es el operador principal de la oración) y la línea 2 está inferyendo una de las conjunciones de esa conjunción en la línea 1. (Basta pensar en la “A v B” como la “p” y la “~ (C ⋅ D)” como la “q”.)
La siguiente regla que vamos a introducir se llama “conjunción” y es como el reverso de la simplificación. (No confunda la regla llamada conjunción con el tipo de proposición compleja llamada conjunción.) La conjunción tiene la siguiente forma:
1. p
2. q
3. p ⋅ q
Lo que dice esta regla, en palabras, es que si has hecho valer dos proposiciones distintas, entonces tienes derecho a hacer valer la conjunción de esas dos proposiciones. Como antes, es importante darse cuenta de que cualquier inferencia que tenga la misma forma que conjunción es una inferencia válida. Por ejemplo,
1. A B
2. C v D
3. (A B) ⋅ (C v D)
es una inferencia válida porque tiene la misma forma que la conjunción. Simplemente estamos uniendo dos proposiciones juntas; no importa si esas proposiciones son atómicas o complejas. En este caso, por supuesto, las proposiciones que estamos uniendo son complejas, pero mientras esas proposiciones ya hayan sido afirmadas como premisas en el argumento (o derivadas por alguna otra forma válida de inferencia), podemos unirlas juntas en una conjunción.
La siguiente forma de inferencia que presentaremos se llama “silogismo disyuntivo” y tiene la siguiente forma:
1. p v q
2. ~p
3. q
En palabras, esta regla establece que si hemos hecho valer una disyunción y hemos hecho valer la negación de uno de los disjuntos, entonces tenemos derecho a hacer valer el otro disjunto. Una vez que lo piensas, esta inferencia debería ser bastante obvia. Si estamos dando por sentada la verdad de los locales —que o p o q es verdad; y que p no es verdad—entonces tiene que seguir que q es verdad para que la disyunción original sea cierta. (Recuerda que debemos asumir que las premisas son verdaderas al evaluar si un argumento es válido). Si afirmo que es cierto que ya sea Bob o Linda se robaron el diamante, y afirmo que Bob no se robó el diamante, entonces tiene que seguir que Linda lo hizo. Eso es un silogismo disyuntivo. Como antes, cualquier argumento que tenga esta misma forma es un argumento válido. Por ejemplo,
1. ~A v (B ⋅ C)
2. ~~A
3. B ⋅ C
es una inferencia válida porque tiene la misma forma que el silogismo disyuntivo. La primera premisa es una disyunción (ya que la cuña es el operador principal), la segunda premisa es simplemente la negación del disyuntor izquierdo, “~A”, y la conclusión es la disyuntiva derecha de la disyunción original. Te puede ayudar a ver la forma del argumento si tratas a “~A” como la p y a “B ⋅ C” como la q. Observe también que la segunda premisa contiene una doble negación. Tu profesor de inglés puede decirte que nunca uses dobles negativos, pero en lo que respecta a la lógica, no hay absolutamente nada de malo en una doble negación. En este caso, nuestro disjunto izquierdo en la premisa 1 es en sí mismo una negación, mientras que la premisa 2 es simplemente una negación de ese disjunto izquierdo.
La siguiente regla que presentaremos se llama “adición”. No es una regla tan “obvia” como las que hemos introducido anteriormente. No obstante, una vez que entiendas las condiciones bajo las cuales una disyunción es verdadera, entonces debería ser obvio por qué esta forma de inferencia es válida. La adición tiene la siguiente forma:
1. p
2. p v q
Lo que dice esta regla, en palabras, es que si hemos hecho valer alguna proposición, p, entonces tenemos derecho a hacer valer la disyunción de esa proposición p y cualquier otra proposición q deseamos. Aquí está la simple justificación de la regla. Si sabemos que p es verdad, y una disyunción es verdadera si al menos uno de los disjuntos es cierto, entonces sabemos que la disyunción p v q es verdadera aunque no sepamos si q es verdadera o falsa. ¿Por qué? Porque no importa si q es verdadero o falso, ya que ya sabemos que p es verdad. Lo más difícil de entender de esta regla es por qué alguna vez querríamos usarla. La mejor respuesta que puedo darte para eso ahora mismo es que nos puede ayudar a la hora de hacer pruebas. 3
Como antes, es importante darse cuenta de que cualquier argumento que tenga esta misma forma, es un argumento válido. Por ejemplo,
1. A v B
2. (A v B) v (~C v D)
es una inferencia válida porque tiene la misma forma que la suma. La primera premisa afirma una afirmación (que en este caso es compleja, una disyunción) y la conclusión es una disyunción de esa afirmación y alguna otra afirmación. En este caso, esa otra afirmación es en sí misma compleja (una disyunción). Pero un argumento o inferencia puede tener la misma forma, independientemente de que los componentes de esas oraciones sean atómicos o complejos. Esa es la lección importante que he estado tratando de profundizar en esta sección.
La final de nuestras 8 formas válidas de inferencia se llama “dilema constructivo” y es la más complicada de todas ellas. Puede ser de gran ayuda introducirlo usando un ejemplo. Supongamos que razoné así:
El asesino está o bien en el ático o en el sótano. Si el asesino está en el ático entonces está por encima de mí. Si el asesino está en el sótano entonces el suyo está debajo de mí. Por lo tanto, el asesino es _________________ o _________________.
¿Se pueden rellenar los espacios en blanco con las frases que harían válido este argumento? Supongo que puedes. Debería ser bastante obvio. La conclusión del argumento es la siguiente:
El asesino está por encima de mí o por debajo de mí.
Que este argumento sea válido debería ser obvio (¿te imaginas un escenario donde todas las premisas sean verdaderas y sin embargo la conclusión sea falsa?). Lo que podría no ser tan obvio es la forma que tiene este argumento. Sin embargo, deberías poder identificar esa forma si utilizas las herramientas que has aprendido hasta ahora. La primera premisa es una disyunción. La segunda premisa es una declaración condicional cuyo antecedente es el disyuntor izquierdo de la disyunción en la primera premisa. Y la tercera premisa es una declaración condicional cuyo antecedente es el derecho disjunto de la disyunción en la primera premisa. La conclusión es la disyunción de las consecuentes de los condicionales en las premisas 2 y 3. Aquí está esta forma de inferencia usando símbolos:
1. p v q
2. p r
3. q s
4. r v s
Ahora hemos introducido cada una de las 8 formas de inferencia. En la siguiente sección te guiaré a través de algunas pruebas básicas que utilizan estas 8 reglas.
Ejercicio
Rellene los espacios en blanco con la forma válida de inferencia que se esté utilizando y las líneas de las que se deduce la inferencia. Nota: la conclusión se escribe a la derecha de la última premisa, siguiendo los símbolos “/”.
Ejemplo 1:
1. M ~N
2. M
3. H N /~H
4. ~N Modus ponens, 1, 2
5. ~H Modus tollens, 3, 4
Ejemplo 2:
1. A v B
2. C D
3. A C
4. ~D /fk B
5. A D Silogismo hipotético, 3, 2
6. ~A Modus tollens, 5, 4
7. B Silogismo disyuntivo, 1, 6
# 1
1. A ⋅ C /fk (A v E) ⋅ (C v D)
2. A _________________
3. C _________________
4. A v E _________________
5. C v D _________________
6. (A v E) ⋅ (C v D) ______________
# 2
1. A (B D)
2. ~D
3. D v A /~B
4. A _________________
5. B D _________________
6. ~B _________________
# 3
1. A ~B
2. A v C
3. ~~B ⋅ D /fk C
4. ~~B _________________
5. ~A _________________
6. C _________________
#4
1. A B
2. A ⋅ ~D
3. B C /C ⋅ ~D
4. A _________________
5. A C _________________
6. C _________________
7. ~D _________________
8. C ⋅ ~D _________________
#5
1. C
2. A B
3. C D
4. D E /E v B
5. C E _________________
6. C v A _________________
7. E v B _________________
#6
1. (A v M) R
2. (L R) ⋅ ~R
3. ~ (C ⋅ D) v (A v M) /~ (C ⋅ D)
4. ~R _______________
5. ~ (A v M) _______________
6. ~ (C ⋅ D) _______________
#7
1. (H ⋅ K) L
2. ~R ⋅ K
3. K (H v R) /L
4. K _________________
5. H v R _________________
6. ~R _________________
7. H _________________
8. H ⋅ K _________________
9. L _________________
#8
1. C B
2. ~D ⋅ ~B
3. (A (B C)) v D
4. A v C /B C
5. ~D _________________
6. A (B C) _____________
7. ~B _________________
8. ~C __________________
9. A __________________
10. B C __________________
11. ~B __________________
12. (B C) v B __________________
3 Una mejor respuesta es que necesitamos esta regla para hacer de este conjunto de reglas que estoy presentando un sonido un conjunto completo de reglas. Es decir, sin ella habría argumentos que son válidos pero que no podemos mostrar son válidos usando este conjunto de reglas. En áreas más avanzadas de la lógica, como la metalógica, los lógicos intentan probar cosas sobre un determinado sistema de lógica, como probar que el sistema es sólido y completo.


