2.14: Lógica Categórica
- Page ID
- 101186
Considera el siguiente argumento:
1. Todos los humanos son mortales
2. Todas las cosas mortales mueren
3. Por lo tanto, todos los humanos mueren
Si tuviéramos que aplicar la prueba informal de validez (del capítulo 1) a este argumento, veríamos que el argumento es válido porque no es posible imaginar un escenario en el que las premisas sean verdaderas y sin embargo la conclusión sea falsa. Sin embargo, mira lo que sucede si tratamos de traducirlo usando lógica proposicional. Dado que “todos los humanos son mortales” es atómico, (es decir, no contiene ningún operador funcional de verdad) podemos traducirlo usando la constante “H” La segunda premisa, “todas las cosas mortales mueren”, también es atómica, por lo que podemos traducirla usando la constante, “M” Por último, la conclusión, es otra afirmación atómica más, “Todos los humanos mueren”, que podemos traducir “D.” Pero entonces la forma de nuestro argumento es justamente esta:
1. H
2. M
3.
El problema es que este argumento no es válido, lo que podemos ver claramente construyendo una tabla de verdad. Dado que hay tres componentes atómicos diferentes, nuestra tabla de verdad será de 8 filas. (En la siguiente tabla de verdad, dado que las columnas de referencia simplemente serían idénticas a las columnas de premisa y conclusión, simplemente colapsé las dos para que la tabla de verdad sea menos redundante).
| H | M | D |
| T | T | T |
| T | T | F |
| T | F | T |
| T | F | F |
| F | T | T |
| F | T | F |
| F | F | T |
| F | F | F |
Observe la segunda fila de la tabla de la verdad (que he escrito en negrita). Las premisas son ambas verdaderas en esa fila y sin embargo la conclusión es falsa. Eso quiere decir que este argumento no pasa la prueba de validez de la tabla de verdad y por lo tanto no es válido. Pero claramente este argumento es válido. Si es cierto que todos los humanos son mortales y que todas las cosas mortales mueren, entonces debe ser cierto que todos los humanos mueren. Lo que este argumento revela es una de las limitaciones de la lógica proposicional. Hay algunos argumentos que son intuitivamente válidos (como éste) pero que no se puede demostrar que sean válidos utilizando los métodos de la lógica proposicional. Esto demuestra que necesitamos otro tipo de lógica formal para poder capturar una gama más amplia de inferencias lógicamente válidas. La lógica categórica nos permite complementar la lógica proposicional con un método formal que manejará argumentos como este que la lógica proposicional es incapaz de manejar.
La lógica categórica es la lógica que aborda la relación lógica entre declaraciones categóricas. Una declaración categórica es simplemente una declaración sobre una categoría o tipo de cosa. Por ejemplo, la primera premisa del argumento anterior es una afirmación sobre las categorías de humanos y cosas que son mortales. La segunda premisa es una declaración sobre las categorías de cosas que son mortales y cosas que mueren. Por último, la conclusión es una afirmación sobre los humanos y las cosas que mueren. Si bien se puede pensar que este argumento como una forma similar a un silogismo hipotético, es distinto de un silogismo hipotético porque las premisas no están compuestas por dos proposiciones atómicas diferentes. Más bien, cada premisa contiene solo una proposición atómica.
En la lógica categórica, los términos lógicos (análogos a la verdad operadores funcionales de la lógica proposicional) son los términos “todos” y “algunos”. En contraste con la lógica proposicional, en la lógica categórica usaremos letras mayúsculas para representar categorías de cosas en el mundo, en lugar de proposiciones atómicas. Así, podemos representar el enunciado:
Todos los humanos son mortales
como
Todas las H son M
donde “H” significa la categoría de “humanos” y “M” significa la categoría, “cosas que son mortales”. Observe que las categorías son sustantivos o frases sustantivas. Así, en vez de decir que la categoría es “mortal” dije que la categoría es “cosas que son mortales”. Es importante reconocer la diferencia entre cómo se están utilizando las letras mayúsculas en la lógica categórica y cómo se usaron en la lógica proposicional. En lógica categórica, las letras mayúsculas representan frases sustantivas que denotan categorías de cosas en el mundo, por ejemplo, “autos” o “cosas que son hechas por el hombre” o “mamíferos” o “cosas que son rojas”.
En lógica categórica, usaremos lo que se llama diagramas de Venn para representar las relaciones lógicas entre los diferentes tipos de declaraciones categóricas. Un diagrama de Venn es simplemente una forma de representar gráficamente la relación lógica entre dos declaraciones categóricas diferentes. A continuación se muestra un diagrama de Venn que representa la afirmación, “todos los humanos son mortales”.
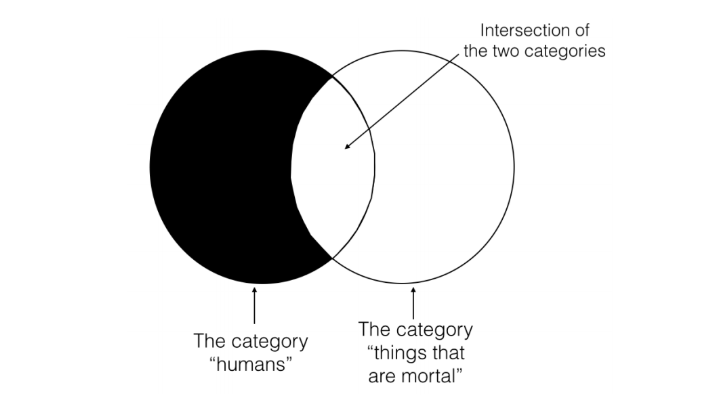
Aquí es cómo entender a este Venn. Hay dos círculos que representan las dos categorías, “humanos” y “cosas que son mortales”. Estas dos categorías se superponen de manera que la intersección de esas dos categorías (es decir, el lugar donde se superponen los dos círculos) representa cosas que son tanto humanas como mortales. Cualquier porción sombreada del diagrama de Venn (por “sombreado” significaré “oscurecido”) representa que no hay nada en esa área de la categoría. Entonces el anterior Venn dice que no hay nada en la categoría “humanos” que no esté también en la categoría “cosas que son mortales”. El anterior Venn también permite que haya cosas que están en la categoría “cosas que son mortales” pero que no están en la categoría “humanos” (que es como debería ser ya que, por supuesto, los perros son mortales y sin embargo no humanos). Entonces, la razón por la que la categoría “cosas que son mortales” se deja sin sombra es que al decir “todos los humanos son mortales” dejo abierta la posibilidad de que haya cosas que no son humanas y aún mortales.
Como se señaló anteriormente, la afirmación, “todos los humanos son mortales”, tiene una forma particular:
Todos los H son M.
Esta es una de las cuatro formas categóricas. La forma en que representaremos estas formas categóricas generalmente es con una “S” (que significa “término sujeto”) y una “P” (que significa “término predicado”). Así, la afirmación categórica, “todos los humanos son mortales”, tiene la siguiente forma categórica:
Todas las S son P
La forma en que interpretamos declaraciones de esta forma es la siguiente: todo en la categoría S también está en la categoría P. Esta forma de declaración es lo que llamamos una “afirmativa universal”, ya que es una afirmación universal que no contiene una negación. Hay otras tres formas de declaración categórica con las que tendrás que familiarizarte para poder hacer lógica categórica. Aquí están (con el nombre del tipo de declaración entre paréntesis a la derecha:
No S son P (negativo universal)
Algunas S son P (particular afirmativas)
Algunos S no son P (particular negativo)
Aquí hay tres ejemplos de declaraciones que tienen estas tres formas (respectivamente):
No hay reptiles que den a luz
Algunas aves son más altas que el presidente Obama
Algunas aves no vuelan
Observe que aunque estas tres declaraciones no tienen exactamente la misma forma que las formas de declaración anteriores, pueden traducirse a esas mismas formas. Todo lo que tenemos que hacer es averiguar la frase sustantiva que describe cada categoría a la que se refiere el enunciado. Empecemos con “ningún reptiles da a luz viva”. Esta afirmación categórica se refiere a dos categorías distintas: la categoría de “reptiles” y la categoría de “cosas que dan a luz viva”. Observe, nuevamente, que agregué “cosas que...” al predicado de la oración (“dar a luz viva”) porque “dar a luz viva” no es una descripción de una categoría. Más bien, la manera de describir la categoría es con la frase sustantiva, “cosas que dan a luz viva”. Usando estas dos descripciones de categorías, podemos traducir esta oración para que tenga la misma forma que su forma categórica. Todo lo que tenemos que hacer es sustituir en el nombre de la categoría de sujeto (es decir, el término “S”) y la descripción de la categoría de predicado (es decir, el término “P”). Hacer eso dará como resultado la siguiente frase:
No hay reptiles son cosas que dan a luz viva
Si bien esta frase suena extraña en inglés, tiene la misma forma que la forma categórica, ninguna S es P, y esta traducción nos permite ver claramente que sí y así ver cuáles son las dos categorías. Así es como se ve el diagrama de Venn para esta declaración:
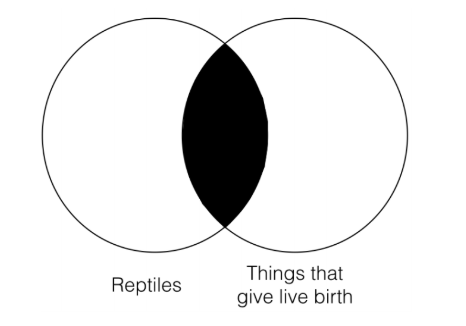
Este diagrama de Venn representa que no hay nada en la intersección de las dos categorías, “reptiles” y “cosas que dan a luz viva”. Si lo piensas, esto es exactamente lo que decía nuestra declaración original: no hay nada que sea a la vez un reptil y dé a luz viva.
Veamos la siguiente declaración, “algunos pájaros son más altos que el presidente Obama”. Esta es una declaración no sobre todas las aves, sino sobre algunas aves. ¿Cuáles son las dos categorías? Una categoría es claramente “aves”. La otra categoría es “cosas que son más altas que el presidente Obama”. Eso puede sonar como una categoría extraña, pero es categoría perfectamente legítima. Incluye cosas como avestruces adultos, osos pardos grandes de pie sobre sus patas traseras, jirafas, el Edificio Flatiron, un autobús escolar, etc. Así es como traduciríamos esta frase usando nuestras dos categorías: Algunas aves son cosas que son más altas que el presidente Obama. Nuevamente, aunque esta frase suena extraña en inglés, tiene la misma forma que la forma categórica, algunas S son P, y nos permite ver claramente cuáles son las dos categorías. A continuación se muestra el diagrama de Venn para esta declaración:

Por convención, un asterisco en el diagrama de Venn significa que hay al menos una cosa en esa categoría. Al poner el asterisco en la intersección de las dos categorías, estamos diciendo que hay al menos una cosa que es un pájaro y es más alta que el presidente Obama, que es exactamente lo que decía nuestra frase original.
Por último, consideremos la afirmación, “algunas aves no vuelan”. ¿Cómo traduciríamos esta frase para tener la forma de “algunas S no son P”? El primer paso es obtener las descripciones de las dos categorías usando ya sea sustantivos o frases sustantivas.
El término “S” es fácil; es sólo “pájaros” otra vez. Pero hay que ser un poco más cuidadosos con el término “P”, ya que su predicado contiene una negación. No queremos que ninguna de nuestras categorías contenga una negación. Más bien, la negación está contenida en la forma (es decir, el “no”). La categoría no puede ser simplemente “volar” o incluso “moscas” ya que ninguna de estas es una categoría de cosa. Tenemos que usar nuestro truco de convertir el predicado en una frase sustantiva, es decir, “cosas que vuelan”. Dadas estas dos descripciones de categorías, entonces podemos traducir la oración para que tenga la forma categórica, algunas S no son P:
Algunas aves no son cosas que vuelan
Nuevamente, aunque el inglés suena torpe aquí, tiene la misma forma que la forma categórica, algunas S no son P, y nos permite ver claramente cuáles son las dos categorías. A continuación se muestra el diagrama de Venn para esta declaración:
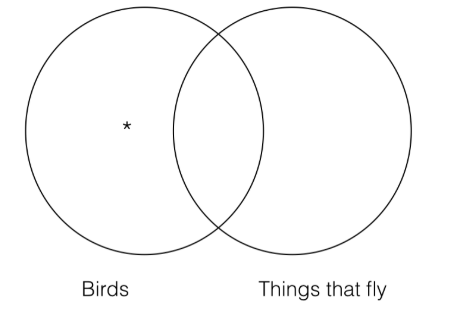
Por convención, un asterisco en el diagrama de Venn significa que hay al menos una cosa en esa categoría. Al poner el asterisco dentro de la categoría “pájaros”, pero fuera de la categoría “cosas que vuelan”, estamos representando que al menos una cosa que es un pájaro no es una cosa que vuela. Esto es exactamente lo que decía nuestra frase original.
Traducir declaraciones categóricas a su forma categórica puede ser complicado. De hecho, es probablemente una de las cosas más complicadas que harás en la lógica formal. No hay una forma sencilla de hacerlo que no sea preguntarse si su traducción captura con precisión el significado de la oración original en inglés. Aquí hay un ejemplo de una declaración categórica complicada:
Nadie me quiere sino a mi madre.
Esta es una afirmación categórica, pero ¿cuál de las cuatro formas categóricas tiene? El primer paso es preguntar a qué dos categorías se refieren en esta frase. Aquí están las dos categorías: “cosas que me aman” y “cosas que son mi madre”. Observe que la categoría no podría ser simplemente “mi madre” ya que esa no es una categoría; es algo en particular. Nuevamente, esto suena extraño, pero es importante recordar que estamos describiendo categorías de cosas. La siguiente pregunta es: ¿qué dice esta frase es la relación entre estas dos categorías? Pista: tiene que ser una de las cuatro formas categóricas (ya que cualquier enunciado categórico puede traducirse a una de estas cuatro formas). La frase está diciendo que las únicas cosas que me aman son las cosas que son mi madre. La forma categórica de la declaración es la forma “todas las S son P”. Así, la frase, traducida a la forma categórica correcta sería:
Todas las cosas que me aman son cosas que son mi madre.
Terminaremos esta sección con un último ejemplo. Considera la siguiente declaración categórica:
El babuino es una bestia temible.
¿Cuál de las cuatro formas categóricas tiene esta afirmación? Si bien el artículo “el”, que a menudo denota particularidades, puede llevar a pensar que se trata de una forma afirmativa particular (algunas S son P), en realidad es una forma afirmativa universal (todas las S son P). Esta frase en inglés tiene el sentido de “los babuinos son bestias temibles” en lugar de “ese (particular) babuino es una bestia temible”. El inglés es extraño, que es lo que hace de la traducción una de las partes más complicadas de la lógica. Entonces, las dos categorías son: “babuinos” y “bestias temibles”. Observe que como “bestias temibles” ya es una frase sustantiva, no tenemos que agregarle “cosas que son...”. Utilizando las dos descripciones de categorías, la traducción a la forma categórica “todas las S son P” es así:
Todos los babuinos son bestias temibles.
En esta sección hemos aprendido qué son los enunciados categóricos, cómo traducir declaraciones categóricas en una de las cuatro formas categóricas, y cómo construir diagramas de Venn para cada una de las cuatro formas categóricas. Los siguientes ejercicios te darán algo de práctica con la parte de traducción; en secciones posteriores aprenderemos a usar diagramas de Venn como método formal para evaluar una determinada clase de argumentos.
Ejercicio
Traducir cada una de las siguientes frases en una de las cuatro formas categóricas (afirmativa universal, negativa universal, afirmativa particular, negativa particular). Asegúrese de que las descripciones de las dos categorías sean sustantivos o frases sustantivas (en lugar de adjetivos o verbos).
1. Los hombres de verdad visten de rosa.
2. Los dinosaurios no son aves.
3. Las aves evolucionaron a partir de los dinosaurios.
4. Algunos mamíferos no son depredadores.
5. Algunos depredadores no son mamíferos.
6. No todos los que deambulan están perdidos.
7. Todos los presidentes no son mujeres.
8. Los boxeadores no son ricos.
9. Si alguien está durmiendo entonces no está consciente.
10. Si alguien está consciente entonces no está durmiendo.
11. Todo bien eso termina bien.
12. Mis amigos son los únicos a los que les importa.
13. Alguien te ama.
14. Jesús ama a todos.
15. Jesús ama a los niños pequeños.
16. Algunas personas no aman a Jesús.
17. Solo los peatones podrán utilizar el Sendero de los Apalaches.
18. Sólo los ciudadanos pueden ser presidentes.
19. Cualquiera que sea hindú cree en Dios.
20. Cualquier cosa que sea barata no es buena.
21. Algunas cosas caras no son buenas.
22. No todos los mamíferos tienen patas.
23. Hay parejas sin hijos.
24. No hay gente que odie el chocolate.
25. Hay gente que odia a los gatos.
26. Nada que sea agudo es seguro.
27. Ningún caniche podría correr más rápido que un guepardo.
28. Ningún corredor profesional es lento.
29. Los babuinos no son amigables.
30. Los cerdos comerán cualquier cosa.


