2.17: Validez de Venn para Silogismos Categóricos
- Page ID
- 101159
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Un silogismo categórico es sólo un argumento con dos premisas y una conclusión, donde cada enunciado del argumento es una afirmación categórica. Como hemos visto, existen cuatro tipos (formas) diferentes de enunciado categórico:
Todos los S son P (afirmativo universal)
No S son P (negativo universal)
Algunos S son P (particular afirmativo)
Algunos S no son P (particular negativo)
Así, las premisas y conclusión de cualquier silogismo categórico serán alguna mezcla de estos diferentes tipos de enunciados. El argumento que di al inicio de la sección 2.13 fue un silogismo categórico. Aquí, nuevamente, está ese argumento:
1. Todos los humanos son mortales
2. Todas las cosas mortales mueren
3. Por lo tanto, todos los humanos mueren
Como podemos ver ahora que hemos aprendido las cuatro formas categóricas, cada una de las afirmaciones en este silogismo es una declaración “afirmativa universal” de la forma, “todas las S son P.” Primero traduzcamos cada enunciado de este argumento para que tenga la forma “todas las S son P”:
1. Todos los humanos son cosas que son mortales.
2. Todas las cosas que son mortales son cosas que mueren.
3. Todos los humanos son cosas que mueren.
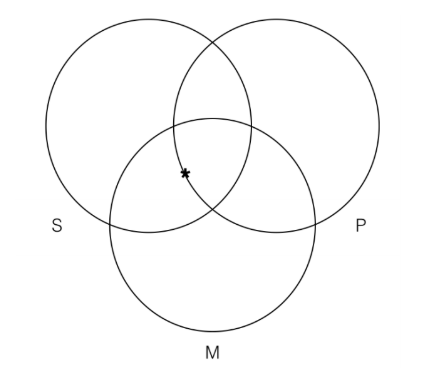
Para determinar la validez de los silogismos categóricos, debemos construir un diagrama de Venn de tres categorías para las premisas y un diagrama de Venn de dos categorías para la conclusión. Así es como se ve el Venn de tres categorías para las instalaciones:
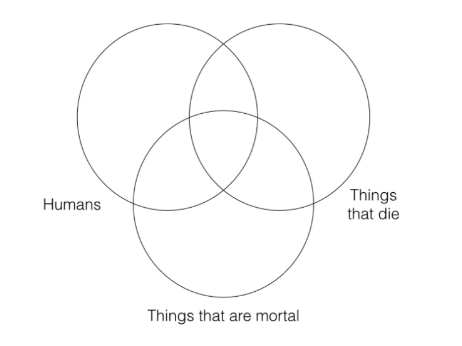
Necesitamos un Venn de tres categorías para las instalaciones ya que las dos premisas se refieren a tres categorías diferentes. La forma en que debes construir el Venn es con el círculo que representa la categoría “S” de la conclusión (es decir, la categoría “humanos”) a la izquierda, el círculo que representa la categoría “P” de la conclusión (es decir, la categoría “cosas que mueren”) a la derecha, y la categoría restante (“cosas que son mortales”) ) en el medio, como he hecho anteriormente. Construir tus tres categorías Venn de esta manera te permitirá determinar fácilmente si el argumento es válido.
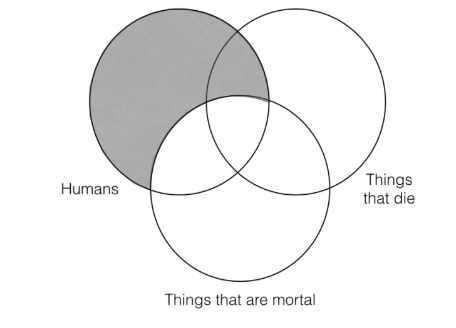
Lo siguiente que debemos hacer es representar la información de las dos primeras premisas en nuestras tres categorías Venn. Comenzaremos con la primera premisa, que dice “todos los humanos son cosas que son mortales”. Eso quiere decir que debemos sombrear cualquier cosa que esté en la categoría “humana”, pero que no esté en la categoría de “cosas que son mortales”, así:
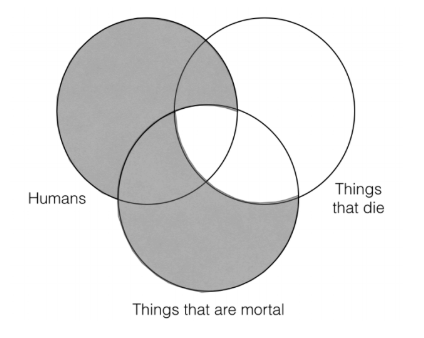
Lo siguiente que tenemos que hacer es rellenar la información para la segunda premisa, todas las cosas que son mortales son cosas que mueren. Eso quiere decir que no hay nada que esté en la categoría “cosas que son mortales” sino que no está en la categoría de “cosas que mueren”. Así que debemos sombrear todas las partes de la categoría “cosas que son mortales” la mentira fuera de la categoría “cosas que mueren”, así:
Lo siguiente que tenemos que hacer es construir un Venn de dos categoría para la conclusión y luego comparar la información representada por los tres categoría Venn para las premisas con los dos categoría Venn para la conclusión.
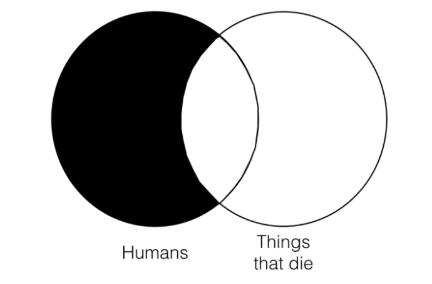
La conclusión representa la información de que no hay nada en la categoría “humanos” que no esté también en la categoría de “cosas que mueren”. También permite que haya cosas que mueren, pero que no son humanos. La premisa Venn también incluye esta misma información, ya que cada parte de la categoría “humanos” que está fuera de la categoría de “cosas que mueren” está sombreada. Así, este argumento pasa la prueba de validez de Venn y por lo tanto es válido ya que no hay información representada en la conclusión Venn que tampoco esté representada en la premisa Venn. Observe que no importa que la premisa Venn contenga más información que la conclusión Venn. Eso es de esperarse, ya que la premisa Venn representa una categoría completamente distinta que la conclusión Venn no es, esto es perfectamente permisible. Lo que no es permisible (y así haría que un argumento falle la prueba de validez de Venn) es si la conclusión Venn contenía información que no estaba ya contenida en la premisa Venn. No obstante, como este argumento no hace eso, es válido.
Intentemos con otro.
1. Todos los pediatras son médicos
2. A todos los pediatras les gustan los niños
3. Por tanto, a todos los médicos les gustan los niños
El primer paso es identificar las tres categorías a las que se hace referencia en este silogismo categórico. Ellos son:
Pediatras
Doctores
Cosas que les gustan a los niños
El siguiente paso es llenar los tres categoría Venn para el local y los dos categoría Venn para la conclusión.

Este argumento no pasa la prueba de validez de Venn porque hay información contenida en la conclusión Venn que no está contenida en la premisa Venn. En particular, la conclusión dice que no hay nada en la categoría “médicos” que esté fuera de la categoría “cosas que gustan de niños”. No obstante, las premisas no representan esa información, ya que la sección de la categoría “médicos” que se encuentra fuera de la intersección de la categoría “cosas que gustan de niños” está sin sombra, lo que representa que ahí puede haber cosas.
En ocasiones al rellenar declaraciones particulares sobre una categoría tres para las instalaciones, se encontrará con un problema que requiere de otra convención para representar con precisión la información en el Venn. Aquí hay un ejemplo donde esto sucede:
1. Algunos mamíferos son osos
2. Algunas criaturas de dos patas son mamíferos
3. Por lo tanto, algunas criaturas de dos patas son osos
Hay tres categorías a las que se hace referencia en este silogismo categórico:
Mamíferos
Osos Criaturas de
dos patas
Como siempre, pondremos el término “S” de la conclusión a la izquierda de nuestras tres categorías Venn, el término “P” a la derecha, y el término restante en el medio, de la siguiente manera:
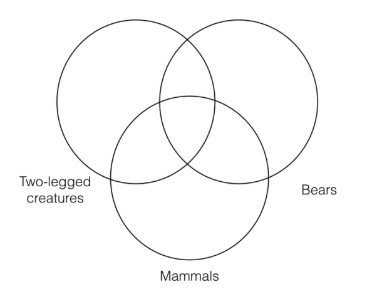
Ahora necesitamos representar la primera premisa, lo que significa que necesitamos poner un asterisco en la intersección de las categorías “mamíferos” y “osos”. Sin embargo, aquí tenemos una elección que hacer. Dado que la intersección de las categorías “osos” y “mamíferos” contiene una sección que está fuera de la categoría “criaturas de dos patas” y una sección que está dentro de la categoría “criaturas de dos patas”, debemos elegir entre representar lo particular como parte de la categoría “criaturas de dos patas” o no.
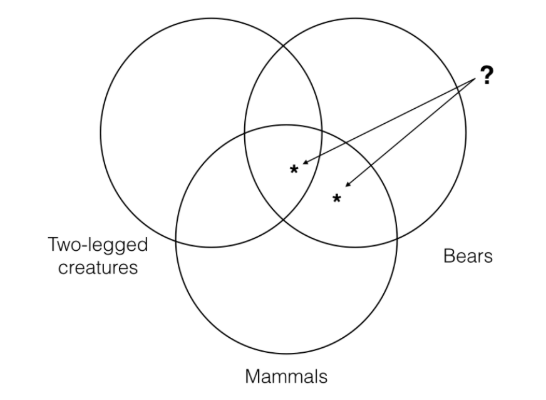
Pero ninguno de estos puede tener razón, ya que la primera premisa no dice nada en absoluto sobre si lo que es a la vez un oso y un mamífero es ¡de dos patas! Así, para representar con precisión la información contenida en esta premisa, debemos adoptar una nueva convención. Esa convención dice que cuando nos encontramos con una situación en la que debemos representar a un particular en nuestras tres categorías Venn, pero la premisa no dice nada de una categoría en particular, entonces debemos poner el asterisco en la línea de esa categoría como lo he hecho a continuación. Cuando hagamos esto, representará que el particular no está ni dentro de la categoría ni fuera de la categoría.
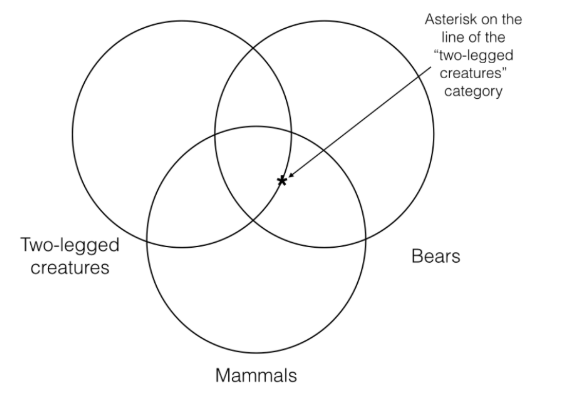
Debemos hacer lo mismo para la segunda premisa, ya que ahí nos encontramos con el mismo problema. Así, al poner el asterisco en la intersección de las categorías “criaturas de dos patas” y “mamíferos”, no podemos poner el asterisco ni dentro ni fuera de la categoría de “osos”. En cambio, debemos poner el asterisco en la línea de la categoría “osos”. Así, utilizando esta convención, podemos representar la premisa Venn y la conclusión Venn de la siguiente manera:
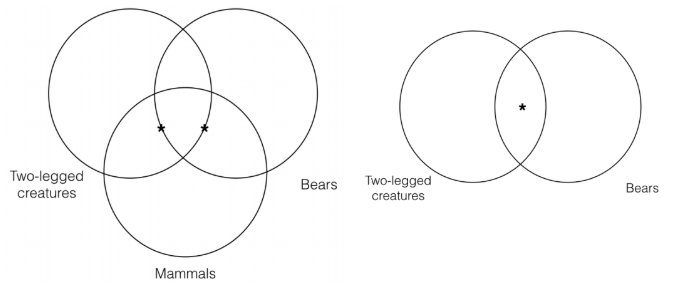
Teniendo en cuenta la convención que acabamos de introducir, podemos ver que este argumento falla la prueba de validez de Venn y, por lo tanto, no es válido. La razón es que la conclusión Venn representa claramente a un individuo en la intersección de las categorías “criaturas de dos patas” y “osos”, mientras que la premisa Venn no contiene tal información. Así, la conclusión Venn contiene información que no está contenida en la premisa Venn, lo que significa que el argumento no es válido.
Cerraremos esta sección con un último ejemplo que ilustrará una estrategia importante. La estrategia es que siempre debemos mapear declaraciones universales antes de mapear declaraciones particulares. Aquí hay un silogismo categórico que ilustra este punto. Esta vez voy a cambiar a solo usar las letras mayúsculas S, P y M para representar las categorías. Recordemos que podemos hacer esto porque la prueba de validez de Venn es un método de evaluación formal donde no tenemos que entender realmente qué representan las categorías en el mundo para determinar si el argumento es válido.
1. Algunas S son M
2. Todas las M son P
3.
Si pensamos en mapear la primera premisa sobre nuestras tres categorías Venn, parece que tendremos que utilizar la convención que acabamos de presentar, ya que la primera premisa es una afirmación categórica particular que menciona solo las categorías S y M y nada sobre la categoría P:
No obstante, resulta que no tenemos que usar esta convención porque cuando mapeamos la premisa 2, que es una afirmación universal, ésta aclara a dónde tiene que ir el asterisco:
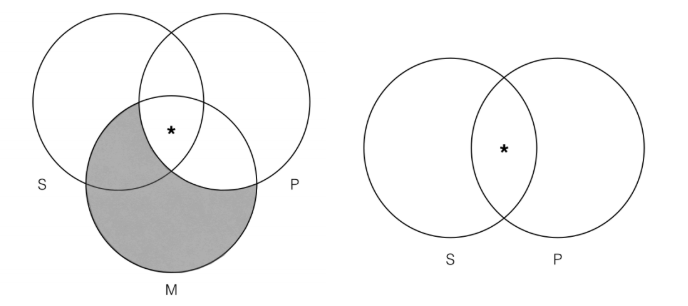
Podemos ver que una vez que hemos mapeado la declaración universal sobre la premisa Venn (a la izquierda), solo hay una sección donde puede ir el asterisco que está en la intersección de S y M. La razón es que una vez que hemos mapeado la premisa de “todos M son P”, y así hemos sombreado cualquier porción de la categoría M que está fuera de la categoría P, sabemos que ese asterisco no puede pertenecer dentro de la categoría M, dado que tiene que estar dentro de la categoría P. Cuando aplicamos la prueba de validez de Venn al argumento anterior, podemos ver que es válida ya que la conclusión Venn no contiene ninguna información que no esté ya contenida en la premisa Venn. La conclusión simplemente dice que hay algo que es tanto S como P, y que la información ya está representada en nuestra premisa Venn. Así, el argumento es válido. El punto de la estrategia aquí es que siempre debemos mapear nuestras declaraciones universales en nuestras tres categorías Venns antes de mapear nuestras declaraciones particulares. La razón es que lo universal puede determinar cómo mapeamos nuestras declaraciones particulares (pero no al revés).
Ejercicio
Utilice la prueba de validez de Venn para determinar si los siguientes silogismos son válidos o no válidos.
1. Todo M es P
Todo M es
S Todo S es P
2. Todo P es M
Todo M es
S Todo S es P
3. Todo M es P
Algunos M es
S Algunos S es P
4. Todo P es M
Algunos M es
S Algunos S es P
5. Todo P es M
Algunos S es
M Algunos S son P
6. Todo P es M
Algunos S no es
M Algunos S no son P
7. Todo M es P
Algunos S no es M
Algunos S no es P
8. Todo M es P
Algunos M no es
S Algunos S no es P
9. No M es P
Algunos S es
M Algunos S no son P
10. No P es M
Algunos S es
M Algunos S no son P
11. No P es M
Algunos S no son
M Algunos S no son P
12. No M es P
Algunos S no son
M Algunos S no son P
13. No P es M
Algunos M no es
S Algunos S no son P
14. No P es M
No M es
S No S es P
15. No P es M
Todo M es
S No S es P
16. No P es M
Todo S es
M No S es P
17. Todo P es M
No S es
M No S es P
18. Todo M es P
No S es
M No S es P
19. Algunos M es P
Algunos M no es S
Algunos S no es P
20. Algunos P es M
Algunos S no son
M Algunos S son P


