11.4.1: Tablas de la Verdad
- Page ID
- 101936
Desarrollemos lo que se llama la semántica formal de la Lógica Sentencial. La semántica se trata, entre otras cosas, de la manera en que la verdad de algunas frases afecta a la verdad de otras oraciones. Se dice que la verdad y la falsedad son los dos valores de verdad que pueden tener las oraciones. Pero una sentencia no puede tener a los dos al mismo tiempo.
Aquí está la tabla de la verdad que da una imagen de cómo funciona la negación:
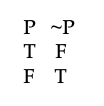
Esta tabla implica, entre otras cosas, que (A & B) y ~ (A & B) tienen valores de verdad opuestos, como se puede ver dejando que P abrevie “(A & B)” en la tabla de verdad.
Aquí hay una tabla de verdad sobre cómo 'v' afecta a los valores de verdad de una oración:
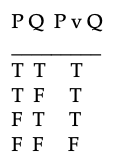
La última línea de esta tabla implica que si la oración A (cuando se sustituye por P) fuera falsa y la oración B (sustituida por Q) fuera falsa, entonces la oración A v B tendría que ser falsa. Pero la tabla no se aplica sólo a las letras de oraciones simples. La última línea también implica que si la oración C & A es falsa y la oración C & B es falsa, entonces la oración (C & A) v (C & B) también es falsa.
Aquí está la tabla de la verdad para &
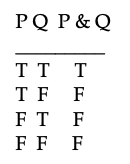
La &-tabla te dice que la única manera de que una oración & sea verdadera es que ambas oraciones componentes sean verdaderas. Por ejemplo, la única manera para que (A v B) & (C v A) sea cierto es que (A v B) sea verdadero y (C v A) sea verdadero.
Aquí está la tabla de la verdad para →
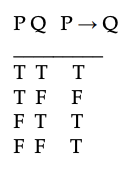
Puedes construir tablas de verdad más grandes para ayudarte a descubrir los valores de verdad de oraciones complicadas a partir de conocer los valores de verdad de sus letras de oraciones componentes. Aquí hay una tabla de verdad para (A & (A → B)) → B. Las columnas intermedias para A → B y para A & (A → B) son nuestro “trabajo de cero” para ayudarnos a averiguar el valor de verdad de la oración más grande.
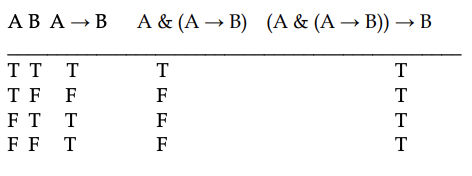
Necesitas una fila de una tabla de verdad para cada forma en que puedas asignar Ts y Fs a las letras de oración componentes. Si hubiera una letra de tercera oración como C en una oración formal, entonces su tabla de verdad necesitaría ocho filas en lugar de cuatro. ¿Cómo nos dimos cuenta de que una T pertenece a la última fila de la última columna de la tabla anterior? Hicimos uso del hecho de que la oración (A & (A → B)) → B es básicamente una → oración cuya if-part es F [como encontramos haciendo el trabajo scratch] y cuya entonces parte es F. Entonces notamos que la tabla de verdad para P→Q dice que, cuando P tiene el valor de verdad F y Q tiene el valor F, deberíamos asignar T a P→Q. Por eso una T pertenece en la fila inferior de la columna derecha de la tabla anterior.
Ejercicio\(\PageIndex{1}\)
¿Cuál es el valor de verdad de E v (F & G) en una fila de la tabla de verdad donde E es falso y F y G son ambos verdaderos?
- Contestar
-
Es verdad. Si F y G son verdaderas, entonces F&G tiene que ser verdad. Pero eso hace que el lado derecho de la 'v' sea cierto, y la tabla de la verdad para 'v' requiere entonces que la oración completa sea verdadera.
Por cada oración de Lógica Sentencial, por más larga que sea la oración, podemos construir su tabla de verdad de esta manera y averiguar las condiciones (filas) bajo las cuales es verdadera y las condiciones bajo las cuales es falsa. Esta característica de la Lógica Sentencial se llama la funcionalidad de verdad de la Lógica Sentencial.
Para decir un poco más de semántica, podemos definir una oración lógicamente verdadera o una tautología en Lógica Sentencial para que sea una oración que sea cierta sin importar cuáles sean los valores de verdad de sus simples letras. Por ejemplo, A v ~A es una tautología, pero A v B no lo es. A v B puede ser verdadero o puede ser falso dependiendo de los valores que tengan A y B. Saldrá falso si A y B son ambos falsos, como se podría comprobar trabajando en la tabla de la verdad. Una frase que siempre es falsa ya no más cuáles son los valores de la verdad de sus simples letras se llama contradicción. A & ~A es una contradicción. La mayoría de las oraciones de Lógica Sentencial no son ni tautologías ni contradicciones. Llamamos a tales oraciones contingentes. Por ejemplo, la frase A v B es contingente. Así es C. En algunas condiciones son verdaderas y en otras condiciones son falsas.
Volvamos por un momento al inglés y comparemos lo que acabamos de decir sobre las oraciones contingentes de la Lógica Sentencial con oraciones contingentes del inglés. 4La frase “El presidente Eisenhower era un general” es contingente porque podría ser cierta y podría ser falsa. Sin embargo, en realidad es cierto; no es realmente falso. Podría ser falso, no en el sentido de que podría llegar a ser falso, sino sólo en el sentido de que podría haber sido falso si los hechos del mundo hubieran sido diferentes. La frase “El presidente Eisenhower era un general o no lo era” es una verdad lógica, y se podría entender que era verdad aunque nunca hubiera oído hablar del presidente Eisenhower. No hay manera de cambiar las condiciones o hechos del mundo para que esta frase sea otra cosa que verdadera. Entérate de esto solo estar mirando su forma lógica subyacente y sabiendo cómo funcionan “o” y “negación” en inglés. Ahora, supongamos que hay una persona de la que nunca has oído hablar, dice Sen-Chu. ¿Sabes si la siguiente frase es cierta?
Sen-Chu era y no era un general.
Se puede decir que esto es falso solo por su estructura semántica, por cómo funcionan las palabras “y” y “no”. No importa quién sea esta persona Sen-Chu, la sentencia debe ser falsa. Esta visión que tienes sobre la estructura semántica se refleja en la Lógica Sentencial cuando descubres que la oración compleja A & ~A tiene que ser falsa incluso si no conoces el valor de verdad de A.
Ejercicio\(\PageIndex{1}\)
Una de estas frases es una tautología, una es contingente y la otra es una contradicción. ¿Cuál es cuál?
F & (~F v G)
~F v (B & (B → F))
(C → D) v ~ (C → D)
- Contestar
-
contingente, contradicción, tautología.
La negación de una oración p es otra oración q que tiene el valor de verdad opuesto como p en cualquier situación, es decir, en cualquier asignación de Ts y Fs a las letras de oración básica. Es fácil ver que ~A es la negación de A.
Se dice que dos afirmaciones son semánticamente equivalentes (o simplemente equivalentes) si están de acuerdo en sus valores de verdad sin importar cuál sea la situación, es decir, sin importar qué asignación de Ts y Fs a sus letras de oración básica. A es equivalente a ~~A. B es equivalente a B v B. ~A es equivalente a A → (B & ~B).
Ejercicio\(\PageIndex{1}\)
La frase C v ~B equivale a una y sólo una de las siguientes frases. ¿Cuál?
a. C → B
b. B →
C c. ~B → C
d. B → ~C
e. ~B → ~C
- Contestar
-
b.


