11.4.3: Lógica de 3 Valores
- Page ID
- 101928
Aquí hay un viejo argumento llamado la paradoja del montón. Comienza con un solo grano de arena. Un grano de arena no es un montón de arena. Agregar un grano a esa pila tampoco hará un montón. De hecho, agregar un grano de arena a cualquier cosa que no sea un montón no lo convierte en un montón. Entonces, no hay montones de arena.
Pero claro que hay montones de arena, por lo que debe haber algún problema con el razonamiento. En la lucha con la lógica de la vaguedad, un pequeño número de logísticos sugieren que debe haber algún punto preciso donde el no-montón se convierta en un montón. Muchos otros recomiendan usar lo que llamamos una lógica de 3 valores para permitir que algunas pilas sean montones, algunas no sean montones y otras estén en el medio. Estos logísticos recomiendan decir que en estos casos intermedios la frase “Eso es un montón” no es ni verdadera ni falsa, y se le debe asignar un tercer valor de verdad “ninguno”. Indiquemos este tercer valor de verdad con el símbolo “#” y lo asignemos a la frase “Agregar un grano de arena a cualquier cosa que no sea un montón no lo convierte en un montón” por lo que la oración no es del todo cierta pero tampoco del todo falsa. A lo mejor podemos resolver la paradoja del montón de esta manera.
Antes de decir más sobre los montones, desarrollemos un poco más nuestra lógica formal.
En cuanto a la negación, nuestras intuiciones nos dicen que, si P fuera a abreviar cualquier declaración formal como A, B, C,..., o incluso declaraciones más complicadas que contengan muchas letras mayúsculas, entonces
~P es verdadero si P es falso,
y esperamos que la tabla de la verdad de la negación tenga estas dos filas:
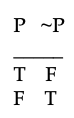
La mayoría de los filósofos y lógicos están contentos con esto. Sin embargo, nuestras intuiciones no son tan claras a la hora de negar una frase que creemos que no tiene un valor de verdad clásico (una T o una F). He aquí por qué. El filósofo y lógico Bertrand Russell creía que todas las oraciones tienen un valor de verdad clásico, pero muchos defensores de la lógica de 3 valores tienen la intuición de que la siguiente oración es otro tipo de oración que no es ni verdadera ni falsa:
El actual rey de Francia es calvo.
Dicen que no es ni verdadero ni falso por la presuposición fallida, por lo que debería obtener un tercer valor de verdad como #. Dicen que la negación
El actual rey de Francia no es calvo
tampoco es verdadero ni falso.

Russell nuevamente no está de acuerdo y dice que ambas frases sobre el rey de Francia son falsas, y en realidad no son negaciones entre sí. En fin, es por eso que los defensores de la lógica de 3 valores dan la siguiente tabla para la negación, donde # es el tercer valor de verdad que representa la falta de un valor de verdad clásico:

El lógico polaco Jan Łukasiewicz utilizó esa tabla en 1924, pero su motivación para desarrollar la lógica de 3 valores no era dar el tercer valor de verdad a oraciones con presuposiciones fallidas ni a frases vagas sino para darle a oraciones sobre el futuro, como “Mañana habrá una batalla marítima”, que él creían que eran incapaces de ser asignados ya sea una T o una F porque mañana no ha pasado. Otros logísticos quieren usar la lógica de 3 valores para oraciones sobre entidades irreales como “Superman y Batman están almorzando”.
Para tener una lógica sentencial completa que sea de 3 valores necesitamos dar tablas de verdad para los símbolos del conector & y v y →. Los logísticos han investigado diversas opciones para estas mesas. Usemos las siguientes tablas que fueron recomendadas por Łukasiewicz.

La forma de leer estas tablas para, digamos A&B, es que los valores de verdad de A provienen de una de las filas, pero el valor de verdad de B proviene de una de las columnas, y el valor de A&B es el valor donde la fila A se encuentra con la columna B. Por ejemplo, si A es # y B es F, entonces miramos la fila # y la columna F y encontramos que A&B es F.
Ejercicio\(\PageIndex{1}\)
Si a la frase “El actual rey de Francia es calvo” se le da el verdad-valor #, ¿cuál es el valor de verdad de estas tres frases cuando se traducen a nuestra lógica sentencial de 3 valores?
El actual rey de Francia es calvo o no calvo.
Si el actual rey de Francia es calvo, entonces el actual rey de Francia es calvo.
No es el caso de que el rey de Francia sea calvo y no calvo.
- Contestar
-
Sea B la frase “El actual rey de Francia es calvo”. Entonces las preguntas están pidiendo los valores de verdad de B v ~B y B → B y ~ (B & ~B). Sus valores son requeridos por las tablas de verdad para ser # y T y #.
Ejercicio\(\PageIndex{1}\)
Consideremos una pregunta más general sobre cómo funciona la lógica de 3 valores. ¿Se puede decir cómo sostiene esa ley de Aristóteles de P v ~P medio excluido en la lógica clásica de 2 valores pero no en nuestra lógica de 3 valores? La ley implica que no importa qué valor de verdad tenga la oración sustituida por P, la oración compleja P v ~P tendrá el valor de verdad T. ¿Por qué esta implicación se mantiene en la lógica de 2 valores pero falla en nuestra lógica de 3 valores?
- Contestar
-
Brevemente, la ley del medio excluido falla en la lógica de 3 valores porque, cada vez que P obtiene el valor #, la oración mayor P v ~P no es cierta; es #.
El anterior Concept Check mostró que P v ~P es una tautología en nuestra lógica de 2 valores pero no logra ser una tautología en nuestra lógica de 3 valores, como esperaríamos. Łukasiewicz quería que fracasara cuando P era una frase que carecía de un valor de verdad clásico como, “Mañana habrá una batalla marítima”.
Pasemos ahora de frases simples a argumentos. Definimos un argumento para ser deductivamente válido en la lógica de 2 o 3 valores si y solo si su conclusión es verdadera siempre que sus premisas sean todas verdaderas. Los argumentos en la lógica de 3 valores se pueden evaluar con tablas de verdad de una manera similar a la lógica habitual de 2 valores, pero ahora hay más filas porque hay más combinaciones de valores de verdad. Por ejemplo, si un argumento está hecho de oraciones de exactamente dos letras de oración A y B, entonces en lugar de las cuatro filas de tablas de verdad clásicas hay nueve filas. Necesitará las siguientes nueve filas para tratar todas las asignaciones posibles de valores de verdad a las letras de oración A y B:

Usemos tablas de verdad para decidir si la siguiente forma de argumento es válida en nuestra lógica de 3 valores. Es válido en lógica de 2 valores y se dice que tiene la forma lógica llamada “modus ponens”.

Aquí está la tabla de la verdad para ese argumento en nuestra lógica de 3 valores:
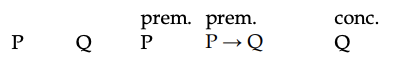
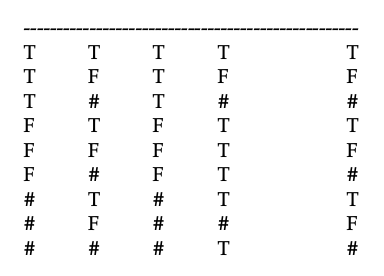
Para utilizar esta tabla para evaluar la validez del argumento, buscará una fila que sirva como contraejemplo al argumento, es decir, una fila en la que las dos premisas son verdaderas pero la conclusión no lo es. Sólo hay una fila en la que las dos premisas son verdaderas, la primera fila, por lo que no es necesario mirar las otras filas. En esa primera fila, Q obtiene el valor T, por lo que la fila no puede ser un contraejemplo. Por lo tanto, el argumento es válido en la lógica de 3 valores. Una moraleja aquí es que si te enfocas en este problema en encontrar solo un contraejemplo, no necesitas construir toda la tabla de la verdad de nueve filas; basta con construir solo la primera fila. Por lo general, al tratar cualquier argumento habrá alguna manera de agilizar la búsqueda de un contraejemplo y evitar construir mesas grandes.
Ejercicio\(\PageIndex{1}\)
Demuestre que este argumento clásicamente válido no es válido en nuestra lógica de 3 valores:
A → B entonces ~A v B
- Contestar
-
En la fila en la que tanto A como B obtienen el valor de verdad #, la premisa es verdadera pero la conclusión no lo es, por lo que esa fila es un contraejemplo


