12.1: La lógica de clases de Aristóteles
- Page ID
- 102232
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Una clase es cualquier colección, grupo o conjunto que se considera como un solo objeto. Todos los símbolos negros en la pantalla de tu computadora hacen una clase, y así lo hacen todos tus dedos. Incluso podrías recolectar mentalmente estas dos clases en la clase combinada de ambos tipos de cosas, aunque esa sería una clase muy extraña. Sorprendentemente, mucha charla ordinaria que no parece ser sobre clases puede interpretarse así que se trata explícitamente de clases, y es por eso que la lógica de clases es más útil de lo que parece ser al principio. Por ejemplo, decir que Obama es presidente puede interpretarse como decir que Obama está en la clase de presidentes. Es miembro de esa clase.
La lógica de clases se enfoca en las clases que se mencionan en sujetos y predicados de oraciones, y se enfoca en la ocurrencia de las palabras clave todo, algunos, ninguno y sus sinónimos. Por ejemplo, la palabra griego se refiere a la clase de los griegos, y la frase “Todos los griegos son europeos” puede interpretarse como diciendo que la clase de griegos está incluida dentro de la clase de los europeos ─es decir, cualquier miembro de la clase de griegos es también miembro de la clase de europeos. La frase “Sócrates era un griego antiguo” no parece ser sobre clases, pero puede interpretarse como diciendo que un objeto (es decir, Sócrates) es miembro de una clase (es decir, la clase de los antiguos griegos). En la lógica de clase, la frase “No los estadounidenses son europeos” se interpretaría como diciendo que la clase de los estadounidenses no se superpone con la clase de los europeos ─es decir, las dos clases no tienen un miembro en común.

Las oraciones sobre clases tienen formas lógicas. Por ejemplo, la frase “Algunos europeos son griegos” tiene la forma “Algunos E son G” donde la letra E significa la clase de europeos y la letra G significa griegos. La frase se interpreta en la lógica de clase como afirmando que algunos miembros de E son miembros de G. La forma de declaración “Todos los N son B” es una versión más breve de “Todos los miembros de la clase N son miembros de la clase B.” En la lógica sentencial, las letras mayúsculas se utilizaron para oraciones o cláusulas, pero aquí en la lógica de clases de Aristóteles, las letras mayúsculas se utilizan para las clases.
Así como las oraciones tienen formas lógicas, también lo hacen los argumentos.

Aquí hay un argumento que se puede parafrasear en inglés para revelar su estructura de clases:
Los nazis son malos.
A los nazis les gusta golpear a los católicos.
Entonces, el gusto de golpear a los católicos es malo.
Su paráfrasis en la lógica de clases:
Todos los miembros de la clase de nazis son miembros de la clase de personas malas.
Todos los miembros de la clase de nazis son miembros de la clase de personas a las que les gusta golpear a los católicos.
Entonces, todos los miembros de la clase de personas a las que les gusta golpear a los católicos son miembros de la clase de personas malas.

Al crear una paráfrasis para su uso en la lógica de clases, buscamos oraciones lógicamente equivalentes en las que el verbo principal sea alguna forma de ser y en las que el sujeto y predicado puedan leerse como sobre clases. Usando algunas abreviaturas obvias de las clases, podemos mostrar la forma lógica del argumento anterior de la siguiente manera:
Todos los N son B
Todos los N son L.A
ll L son B.
donde
N = (la clase de) nazis
B = (la clase de) malas personas
L = (la clase de) todas las personas a las que les gusta golpear a los católicos
La prueba de si realmente hemos encontrado la forma lógica del argumento es si podemos reproducir el argumento sustituyendo las palabras por las letras.
Dos argumentos diferentes en inglés podrían tener la misma forma en la lógica de clases si podemos cambiar la definición de las letras mayúsculas. Por ejemplo, si la letra L fuera a representar a la clase de personas a las que les gusta respirar aire, entonces al sustituir palabras por letras en la forma de argumento anterior, obtendríamos un argumento análogo sobre que a los nazis les gusta respirar aire.
Los nazis son malos.
A los nazis les gusta respirar aire.
Entonces, el gusto por respirar aire es malo.
Los dos argumentos se levantan y caen juntos en la lógica de clase porque son lógicamente análogos, es decir, tienen la misma forma en la lógica de clase. Esta forma en particular es deductivamente inválida, ¿no es así?
Nuestra elección de la letra N fue arbitraria. Podemos reescribir argumentos formales en la lógica de clases y obtener la misma forma. Si reemplazamos N por M arriba, obtendríamos esta forma análoga:
Todas las M son B
Todas las M son L.
Todas las L son B.
En la lógica de clases, si estamos hablando de miembros individuales en lugar de clases, la costumbre es usar letras minúsculas. Entonces, si quisiéramos tratar la frase “El pez más grande de nuestro mar no es un mamífero” en la lógica de clase, podríamos elegir la minúscula “b” para “el pez más grande de nuestro mar” y elegir “M” para el predicado “es un mamífero”. Entonces traduciríamos nuestra oración a lógica de clase como “b es NO-M”.
El “NO” no es la negación que se utilizó en la lógica sentencial. Aquí significa el complemento de M, es decir, la clase de todas las cosas no en M.
Ejercicio\(\PageIndex{1}\)
¿Cuál de las siguientes opciones tiene la forma lógica de este argumento sobre las ballenas? (Pista: El orden en que se presentan las premisas en un argumento no es esencial para la validez de un argumento ni para su forma.) Las ballenas son mamíferos, pero el pez más grande de nuestro mar definitivamente no es un mamífero, así que tampoco es una ballena.
- Las papas son productos. No todos los alimentos de engorde son papas, por lo que tampoco todos los alimentos de engorde son productos.
- Esa cosa que se revuelve no tiene columna vertebral. Sin embargo, los peces son el tipo de cosas que sí tienen columna vertebral. Entonces no es un pez.
- Los peces gordos son nadadores. Ningún gato de la casa es un pez gordo, así que ningún gato de la casa es nadador.
- Contestar
-
Respuesta (b). Ambos argumentos tienen esta forma: Todos los W son M. b es NO-M, entonces b es NO-W.

No estás restringido a usar letras mayúsculas simples para una clase. Si te ayuda a recordar mejor su nombre dándole a la clase un nombre más largo, eso está bien. Podrías haber elegido “MAM” como la abreviatura de la clase de mamíferos en lugar de “M”
Ejercicio\(\PageIndex{2}\)
Elija el patrón lógico de clase correcto para el siguiente argumento biológico:
Todos los insectos tienen exactamente seis patas. Entonces ninguna araña es un insecto porque todas las arañas tienen exactamente ocho patas.
Aquí hay cuatro opciones para el patrón. SIX significa la clase de cosas que tienen seis patas.

- Contestar
-
Respuesta (d). Sólo los apartados b) y d) tienen la conclusión correcta por debajo de la línea
Los dos argumentos que aparecen a continuación tienen formas distintas. Cualquier argumento con el formulario de la derecha es válido:
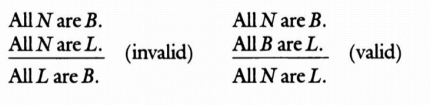
Deberías poder pensar en un contraejemplo a la forma de argumento de la izquierda. Piensa en qué definiciones podrías darle a N, B y L que crearían un argumento con verdaderas premisas y una conclusión falsa.
Sustituir a los nazis por N y a los malos por B y les gusta respirar aire por L producirá un contraejemplo a la forma de la izquierda.
Ejercicio\(\PageIndex{3}\)
Si algunos A son C y todos los C son R, entonces algunos R deben ser A?
- Contestar
-
Sí, este es un razonamiento deductivamente válido en la lógica de clase. No se puede pensar en ninguna definición para las letras que produzca un argumento inválido.
De la respuesta a la comprobación conceptual anterior se puede ver que la lógica deductiva es poner límites a lo que se le ocurra.

Ejercicio\(\PageIndex{4}\)
¿Es ésta una forma de argumento deductivamente válida?
No A son B.
Algunos B son C.
No A son C.
- Contestar
-
No, es deductivamente inválido. Probablemente puedas pensar en algunas definiciones para las letras que producirán un argumento no válido. ¿Qué tal A siendo manzanas y B siendo plátanos y C siendo fruta?


