12.6: Ejercicios
- Page ID
- 102241
■ 1. Encuentra tres clases en el mundo real que tengan las relaciones indicadas en el siguiente diag r am:

2. Dibuja un diagrama en el que la siguiente afirmación sea verdadera, y dibuje uno en el que sea falso: “Solo las cosas que no son portátiles son retornables”. Asegúrese de definir sus etiquetas.
■ 3. Dibuja un diagrama en el que sea cierto que aunque no hay estadounidenses votantes, algunos de ellos son libres y otros no, sin embargo, todos son ricos. En tu diagrama, ¿todos los votantes son ricos?
4. Si todos A son C pero no C son B, entonces algunos A son también B?
■ 5. Encontrar algo que tenga ambas propiedades W y T tiende a confirmar la afirmación “Todos los W son T”; por ejemplo, encontrar un cuervo negro tiende a confirmar la afirmación “Todos los cuervos son negros”.
a. verdadero
b. falso
6. Si todas las cosas no negras son no cuervos, entonces puedes estar seguro de que no hay cuervos albinos.
a. verdadero
b. falso
7. Suponiendo que todas las cosas no negras no son violentas, se deduce con certeza que todas las cosas no violentas no son negras.
a. verdadero
b. falso
8. Aunque todos los cuervos sean negros, no necesariamente se daría el caso de que todo lo que no es negro no sea un cuervo.
a. verdadero
b. falso
9. La oración puede ser utilizada para expresar un argumento inválido. Conviértelo en un argumento deductivamente válido agregando solo la palabra.
Los niños no pagan impuestos en absoluto, porque los niños no son adultos y porque los adultos pagan impuestos.
■ 10. Dar la forma lógica del siguiente argumento en la lógica de clase. Define tus nuevos símbolos, pero deja que M = la clase de las obras de arte modernas. Dibujar los diagramas relevantes para evaluar la validez deductiva del argumento. Evalúa su validez haciendo referencia a su (s) diagrama (s): es decir, digamos, “Estos diagramas muestran que el argumento es válido (o inválido) porque...”
Dado que todas las obras de arte modernas son obras de arte profundas, pero no todas las obras de arte profundas son obras de arte modernas, y debido a que algunas obras de arte religiosas son obras de arte modernas, aunque algunas no lo son, se deduce que algunas obras de arte religiosas no logran ser profundas.
■ 11. La técnica del diagrama Venn-Euler es una forma de probar si algo está mal (no válido) con el patrón de argumentos que se refieren a clases de cosas.
a. verdadero
b. falso
12. Dado un argumento lógico de clase que es deductivamente válido pero poco sólido, la técnica del diagrama puede mostrar por qué no es sólida.
a. verdadero
b. falso
13. Utilice el método de diagramas para determinar la validez o invalidez del siguiente argumento:
Hay médicos que no son ricos, porque todos los médicos son profesionales, sin embargo algunos profesionales no son ricos.
14. Si ningún artículo de la columna C es indeducible, y si la columna C no está vacía de artículos, entonces ¿podemos inferir con certeza que al menos un artículo de la columna C es deducible?
■ 15. ¿Este argumento es deductivamente válido?
Algunos antropoides son subrepticiosos y otros no; de ahí que haya cosas descaradas que no son antropoides porque todos los seres subrepticios son descarados.
■16. ¿Este argumento es deductivamente válido? Usa el método de diagramas, y muestra tu trabajo.
Hay ganadores de premios que no son avariciosos, porque cada participante temprano es ganador de premios y porque uno o más seres avariciosos sí entraron temprano, aunque algunos no.
17. ¿Este argumento es deductivamente válido? Usa el método de diagramas, y muestra tu trabajo.
Hay ganadores de premios que no son avariciosos, porque todos los participantes tempranos son ganadores de premios y algunas personas avariciosas ingresaron temprano y algunos entrantes tempranos no son avariciosos.
18. ¿Es cierta la afirmación “Algunos árabes son dravidianos” en el siguiente diagrama?

a. si
b. no
19. ¿Este argumento es deductivamente válido? Primero, considere si el argumento se maneja mejor con lógica sentencial o lógica de clase.
A las doncellas lunares no les gusta Miller Lite. Si la Bestia controla al planeta Gorp, entonces Xenon está en el poder en esa luna. Si Xenon está en el poder en esa luna, entonces la luna doncella como Miller Lite. Entonces la Bestia no controla al planeta Gorp.
Dar la forma lógica del argumento. Defina sus términos.
20. Uno de los dos argumentos siguientes es deductivamente válido, y el otro no. Identifique el inválido y utilice el método de diagramación de Venn-Euler para defender su respuesta.
A = Árabes D = Dravidianos
- Hay personas biópicas que no son retorcidas porque algunas personas desviadas no son subrepticiosas, y otras lo son, y porque una persona es subrepticia sólo si es biopical.
- Hay personas biópicas que no son desviadas porque algunas personas subrepticiosas no son retorcidas, y otras lo son, y porque cualquier persona es biopical si es subrepticia.
21. Utilice la técnica de diagramas para evaluar la validez de los siguientes argumentos:
a. si algunos A son C, y todos los C son R, entonces algunos R deben ser A
b. No A son B.
Algunos B son C.
Entonces, no A son C.
c. No A son B.
Todas las B son C.
Entonces, ninguna A es C.
22. ¿Qué diagrama demuestra la invalidez deductiva del siguiente argumento?

Ningún simio son osos.
Ningún oso son gatos.
Entonces, ningún simios son gatos.

23. Dibuja un diagrama que demuestre la invalidez deductiva del siguiente argumento que podría dar un político liberal que no esté razonando lógicamente:
Ningún conservador en el Congreso está a favor de ayudar a la humanidad, porque todos los partidarios de la legislación para incrementar los programas de bienestar quieren ayudar a la humanidad, sin embargo ninguno de los conservadores apoya la legislación para incrementar los programas de bienestar.
24. ¿Las siguientes afirmaciones son lógicamente consistentes entre sí? Usa diagramas para defender tu respuesta.
No sólo no son arácnidos bluejays, sino tampoco los diálidos. Aún así, algunas bluejays son catalíticas, pero no todas lo son. Cualquier cosa catalítica es un dializado.
■ 25. Decir que todas las personas que van a este restaurante son niños es decir algo lógicamente equivalente a
a. Sólo las personas que van a este restaurante son niños.
b. Sólo los niños (son las personas que) van a este restaurante.
c. Ni a ni b.
d. Tanto a como b.
■ 26. Qué pares de formularios de declaración de la siguiente lista son lógicamente equivalentes a
el uno al otro? Al responder, use solo las letras minúsculas, no las formas de declaración en sí mismas.
a. No Aare B.
b. No B son A
c. Todos son no-B.
d. Todos los no-B son A.
e. Sólo que no -A son B.
27. ¿Qué pares de declaraciones de la siguiente lista son lógicamente equivalentes entre sí? Al contestar, use solo las letras, no las declaraciones. Pista: Usa la lógica aristotélica.
a. Toda cosa de mano no es retornable.
b. Ninguna cosa retornable es de mano.
c. Todas las cosas no retornables son de mano.
d. Solo las cosas que no son de mano son retornables.
e. Ninguna cosa de mano es retornable.
■ 28. ¿Estos son lógicamente equivalentes? Si no, ¿por qué no?
a. No todas las obras de arte profundas son modernas.
b. No todas las obras de arte profundas son obras de arte modernas.
29. Durante la presidencia de Ronald Reagan, el fiscal general de Estados Unidos, Edwin Meese III, criticó la decisión Miranda de la Suprema Corte que detallaba los derechos legales de las personas acusadas que la policía debe respetar. Meese dijo: “La cosa es que no tienes muchos sospechosos que sean inocentes de un crimen... Si una persona es inocente de un delito, entonces no es sospechoso”. Una de las siguientes afirmaciones es lógicamente equivalente a lo que dijo Meese en su última frase. Es decir, dijo Meese
a.- Si una persona no es inocente de un delito, no es sospechoso.
b. Ningún sospechoso en un delito es inocente.
c. Ninguna persona que no sea inocente de un delito es sospechosa.
d. Todos los sospechosos en delitos son inocentes.
e.- Si una persona es inocente de un delito, entonces no es culpable del delito.
■ 30. Probemos algo más de terminología del amigo de todos, el Servicio de Impuestos Internos de Estados Unidos.

Si ningún artículo de la columna C es deducible, entonces ¿podemos inferir con certeza que no hay artículos deducibles de la columna C? ¿Y viceversa? ¿Qué puede concluir sobre si las dos afirmaciones son lógicamente equivalentes?
31. Sofá y sofá son términos equivalentes, es decir, son sinónimos. Ahora considera raro el término. ¿El término está más cerca de ser equivalente a inusual o más bien a muy inusual? Si alguien no estuvo de acuerdo contigo sobre esto, ¿qué podrías hacer para demostrar que la persona está equivocada?
32. Decir que solo las personas que van a este restaurante son niños es decir algo lógicamente equivalente a
a. todas las personas que van a este restaurante son niños.
b. Todos los niños van a este restaurante.
c. Ni a ni b.
d. Tanto a como b.
■ 33. Supongamos que alguien dice: “Sólo los niños van a los restaurantes Chuck E. Cheese”.
i. ¿La siguiente frase, si es verdad, sería un contraejemplo?
Algunos niños en Rusia no van a los restaurantes Chuck E. Cheese.
ii. ¿Qué tal esto como contraejemplo en su lugar?
Soy un adulto, no un niño, y voy a los restaurantes Chuck E. Cheese.
34. Considera este argumento:
Todos los cilindros contienen petróleo, ya que cada uno tiene una tapa azul y solo los contenedores de petróleo tienen tapas azules.
¿De la segunda premisa se desprende que algunas cosas pueden tener tapas azules pero no ser contenedores de petróleo?

Soluciones
1 A = fruto, B = naranjas, C = cosas que crecen en los árboles.
3 Hay muchos diagramas aceptables. La relación entre votantes y ricos no está fijada por la sentencia. En consecuencia, tiene margen de maniobra sobre a dónde puede ir la región de los votantes. Puede salir de la zona rica, puede cruzarla, o puede estar completamente dentro de ella, siempre que el área de votantes esté completamente separada del área estadounidense. En el siguiente diagrama todos los votantes son ricos, pero esto no necesita ser cierto en otros diagramas aceptables
5 Respuesta (a).
10 Aunque no se le pidió el formulario estándar, aquí está:
Todas las obras de arte modernas son obras de arte profundas.
No todas las obras de arte profundas son obras de arte modernas.
Algunas obras de arte religiosas son obras de arte modernas.
Algunas obras de arte religiosas no son obras de arte modernas.
Entonces, algunas obras de arte religiosas no logran ser profundas.
La forma lógica del argumento es:
Todas las M son P.
No todas las P son M.
Algunas R son M.
Algunas R no son M.
Por lo tanto, algunas R no son P.
donde usamos estas definiciones:
M = (la clase de) obras de arte modernas
P = las profundas obras de arte
R = obras de arte religiosas
“No todos P son M” significa que no todos los miembros de P son miembros de M.
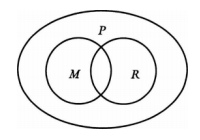
Este diagrama muestra que el argumento es deductivamente inválido porque el diagrama hace que las premisas (de la forma lógica) sean verdaderas mientras que la conclusión es falsa.
11 Respuesta (a).
15 No es válido por la posibilidad de la situación que se muestra en el siguiente diagrama:
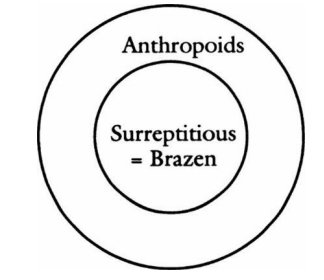
16 Para encontrar la respuesta, traducirla al tipo de inglés que más obviamente habla de clases y que usa los términos todos, algunos, y ninguno en lugar de sus equivalentes.
Todos los participantes anticipados son ganadores de premios.
Algunos seres avariciosos son los primeros en entrar.
Algunos seres avariciosos no son entrantes tempranos.
Algunos ganadores de premios no son avariciosos.
La forma lógica de lo anterior es:
Todos los EE son PW.
Algunos AB son EE.
Algunos AB no son EE.
Algunos PW no son AB.
Dónde
EE = (la clase de) primeros participantes
PW = (la clase de) ganadores del premio
AB = (la clase de) seres avariciosos
Objetivo: Dibujar un diagrama que muestre que el argumento puede tener verdaderas premisas al tiempo que tiene una conclusión falsa, el signo seguro de invalidez deductiva. El siguiente diagrama logra este objetivo:
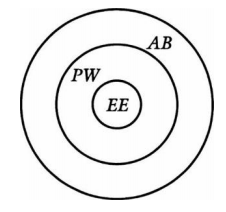
25 Respuesta (b).
26 Todos los pares del grupo {a, b, c, d} son lógicamente equivalentes.
28 Sí, dicen lo mismo, usando el principio de la caridad. Son diferentes gramaticalmente pero no lógicamente. Es posible interpretar el primero como significado medio moderno en el tiempo y el segundo como significado moderno en estilo. No obstante, si haces este último punto, también debes notar que los dos podrían ser (mejor aún, es probable que sean) lógicamente equivalentes; es erróneo decir que definitivamente no son equivalentes. De hecho, si las dos oraciones fueran utilizadas en un razonamiento y sí tuvieran significados diferentes, y si el contexto no lo dejara claro, se acusaría al razonador de cometer la falacia de la equívoco.
30 Sí. Sí. Son equivalentes; son dos formas de decir lo mismo.
33 i. no ii. si


