3.1: OBJETIVOS

La salida producida por un amplificador operacional (o cualquier otro sistema dinámico) en respuesta a un tipo o clase particular de entradas normalmente proporciona la caracterización más importante del sistema. El propósito de este capítulo es desarrollar las herramientas analíticas necesarias para determinar la respuesta de un sistema a una entrada especificada.

Si bien siempre es posible determinar exactamente la respuesta de un sistema lineal a una entrada dada, frecuentemente encontraremos que una mayor comprensión del proceso de diseño resulta cuando una respuesta del sistema se aproxima por la respuesta conocida de una configuración más simple. Por ejemplo, al diseñar un preamplificador de bajo nivel destinado a señales de audio, podríamos estar interesados en mantener la respuesta de frecuencia del amplificador dentro del\(\pm 5\)% de su valor de banda media sobre un ancho de banda particular. Si es posible aproximar el amplificador como un sistema de dos o tres polos, las restricciones necesarias en la ubicación de los polos son relativamente sencillas. De manera similar, si se va a diseñar un amplificador vertical de osciloscopio, una especificación requerida podría ser que el sobredisparo de la salida del amplificador en respuesta a una entrada escalonada sea inferior al 3% de su valor final. Nuevamente, se producen restricciones simples si la función de transferencia del sistema puede aproximarse por tres o menos polos.

Las ventajas de aproximar las funciones de transferencia de sistemas lineales solo se pueden apreciar con la ayuda de ejemplos. El amplificador operacional de circuito integrado LM301A (Este amplificador se describe en la Sección 10.4.1.) tiene 13 transistores incluidos en su trayectoria de transmisión de señal. Dado que cada transistor puede modelarse teniendo dos condensadores, la función de transferencia del amplificador debe incluir 26 polos. Incluso esta estimación es optimista, ya que existe capacitancia distribuida, comparable a capacitancias de transistor, asociada con todos los demás componentes en la trayectoria de la señal.

Figura 3.1 Respuestas escalonadas del amplificador inversor. (\(a\)) Conexión. (\(b\)) Respuesta escalonada con condensador compensador de 220-pF. (\(c\)) Respuesta escalonada con condensador 3.1 de compensación de 12 pF.

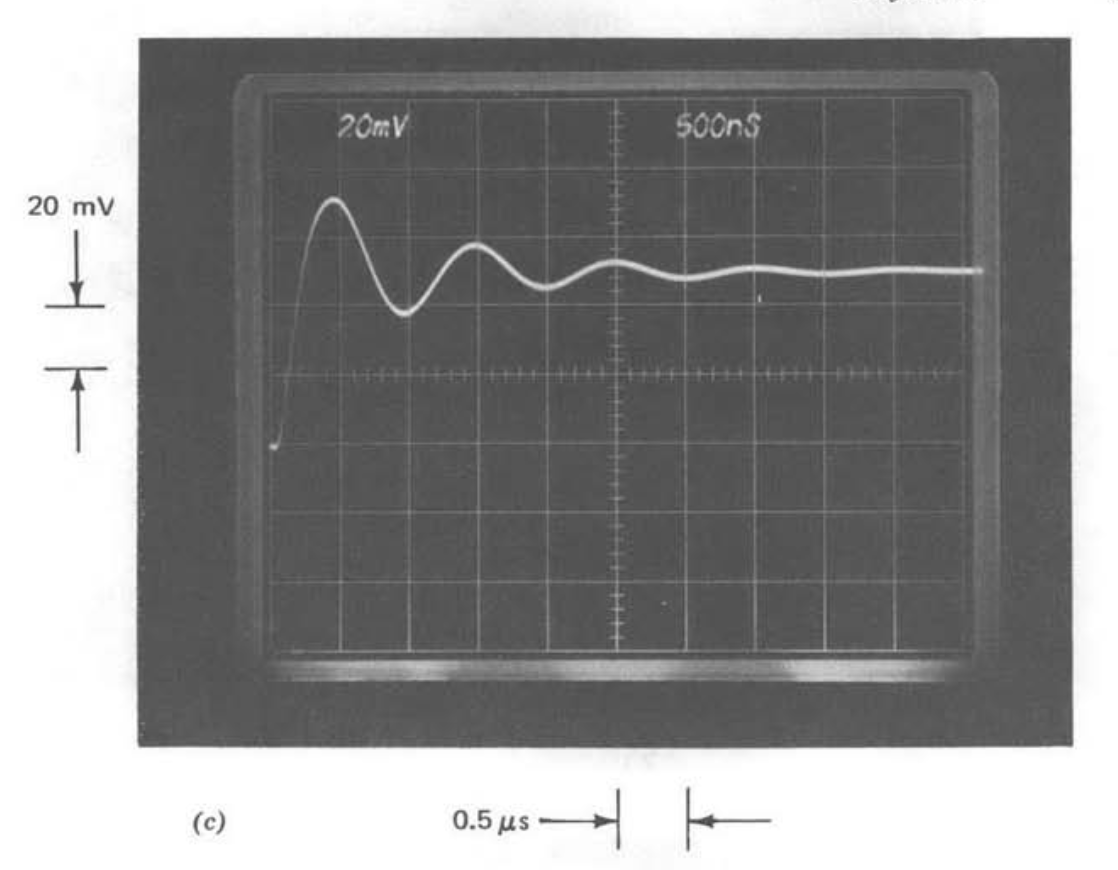
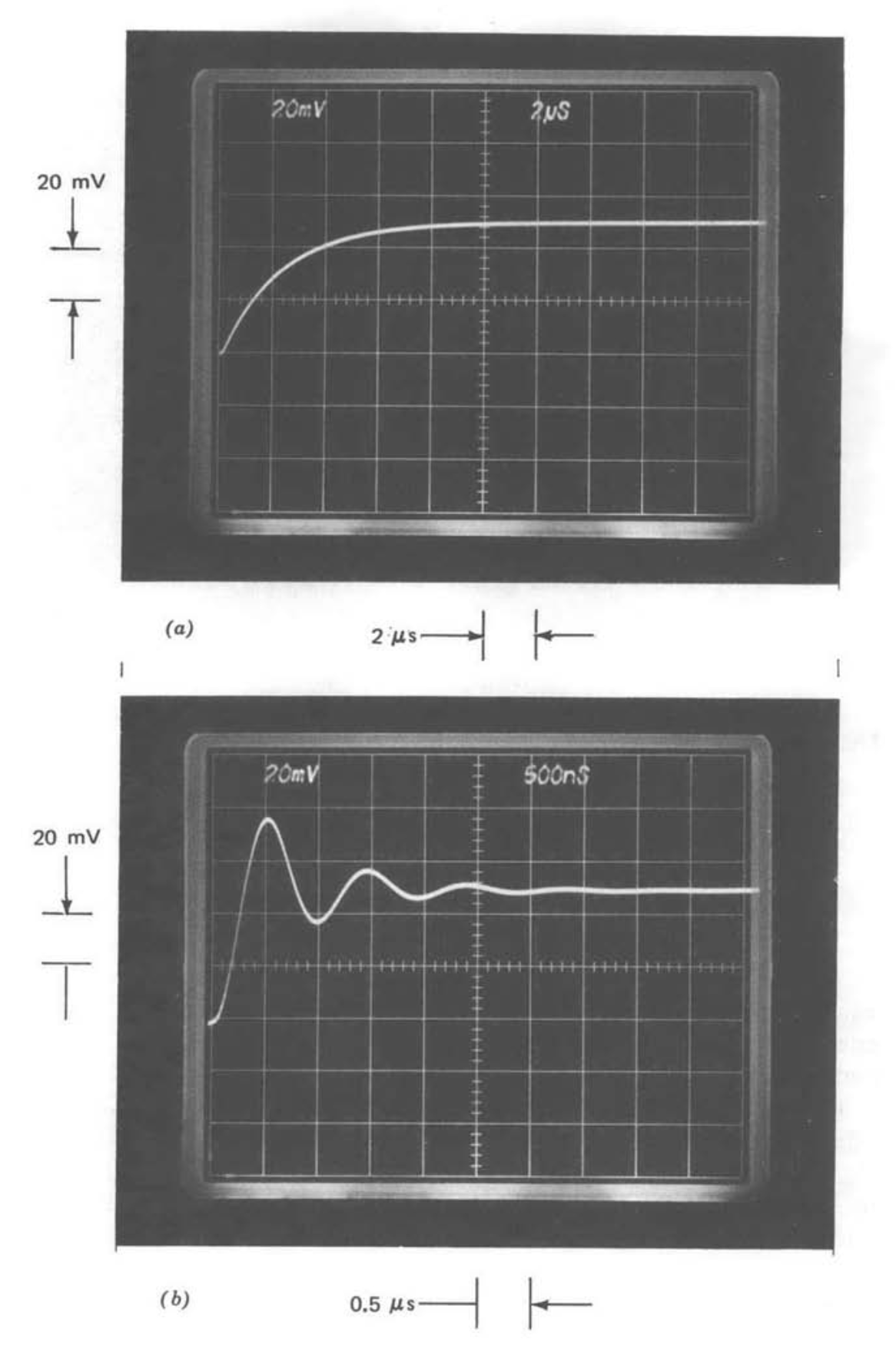
Afortunadamente, las mediciones experimentales de rendimiento pueden salvarnos de la conclusión de que este amplificador es analíticamente intratable. La Figura 3.1\(a\) muestra el LM301A conectado como un inversor de ganancia unitaria. Las figuras 3.1\(b\) y 3.1\(c\) muestran la salida de este amplificador con la entrada un paso de -50-mV para dos valores diferentes de condensador compensador. (La compensación es un proceso mediante el cual la respuesta de un sistema puede ser modificada de manera avanzada, y se describe en detalle en secciones posteriores). Las respuestas de una\(R-C\) red y una\(R-L-C\) red cuando se excitan con pasos de +50 mV suministrados desde el mismo generador utilizado para obtener los transitorios anteriores se muestran en las figuras 3.2\(a\) y 3.2\(b\), respectivamente. Las funciones de transferencia de red son

\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{1}{2.5 \times 10^{-6} s + 1}\label{eq3.1.1} \]

para la respuesta mostrada en la Figura 3.2\(a\) y

\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{1}{2.5 \times 10^{-14} s^2 + 7 \times 10^{-8} s + 1}\label{eq3.1.2} \]

para lo que se muestra en la Figura 3.2b. Concluimos que existen muchas aplicaciones donde las funciones de transferencia de primer y segundo orden de las Ecuaciones 3.1 y 3.2 modelan adecuadamente la función de transferencia de bucle cerrado del LM301A cuando están conectadas y compensadas como se muestra en la Figura 3.1.

Este mismo tipo de proceso de modelado también se puede utilizar para aproximar la función de transferencia de bucle abierto del propio amplificador operacional. Supongamos que la impedancia de entrada del LM301A es grande en comparación con 4.7\(k\Omega\) y que su impedancia de salida es pequeña en comparación con este valor a frecuencias de interés. La función de transferencia de bucle cerrado para la conexión mostrada en la Figura 3.1 es entonces

\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{-a(s)}{2 + a(s)}\label{eq3.1.3} \]

Figura 3.2 Respuestas escalonadas para redes de primer y segundo orden. (\(a\)) Respuesta escalonada para\(V_o (s)/V_i (s) = 1/(2.5 \times 10^{-6} s + 1)\). (\(b\)) Respuesta escalonada para\(V_o (s) /V_i (s) = 1/(2.5 \times 10^{-14} s^2 + 7 \times 10^{-8} s + 1)\).

donde\(a(s)\) está la función de transferencia de bucle abierto descargada del amplificador. Sustituir valores aproximados por ganancia de bucle cerrado (los negativos de Ecuaciones\(\ref{eq3.1.1}\) y\(\ref{eq3.1.2}\)) en Ecuación\(\ref{eq3.1.3}\) y resolución de\(a(s)\) rendimientos

\[a(s) \simeq \dfrac{8 \times 10^5}{s} \nonumber \]

y

\[a(s) \simeq \dfrac{2.8 \times 10^7}{s(3.5 \times 10^{-7} s + 1)} \nonumber \]

como ganancias aproximadas de bucle abierto para el amplificador cuando se compensa con condensadores 220-pF y 12-pF, respectivamente. Veremos que estos valores aproximados son bastante precisos en frecuencias donde la magnitud de la transmisión de bucle está cerca de la unidad.