3.2: LAPLACE TRANSFORMA
- Page ID
- 84208
Se presenta una discusión completa en M. F. Gardner y J. L. Barnes, Transients in Linear Systems, Wiley, Nueva York, 1942.
En esta sección suspendemos temporalmente la notación variable y subíndice utilizada else where y conformamos a la tradición usando una variable minúscula para significar una función de tiempo y el capital correspondiente para su transformación.
Laplace Transforms ofrece un método para resolver cualquier ecuación diferencial lineal invariable en el tiempo y, por lo tanto, se puede utilizar para evaluar la respuesta de un sistema lineal a una entrada arbitraria. Dado que se asume que la mayoría de los lectores han tenido algún contacto con este tema, y dado que no pretendemos utilizar este método como nuestra herramienta analítica primaria, la exposición que aquí se presenta es breve y está dirigida principalmente hacia la introducción de notación y definiciones que serán utilizadas posteriormente.
Definiciones y Propiedades
La transformación de Laplace de una función de tiempo\(f(t)\) se define como
\[\mathcal{L} [f(t)] \triangleq F(s) \triangleq \int_{0}^{\infty} f(t) e^{-st} dt \nonumber \]
donde\(s\) es una variable compleja\(\sigma + j \omega\). La transformada inversa de Laplace de la función compleja\(F(s)\) es
\[\mathcal{L}^{-1} [F(s)] \triangleq f(t) \triangleq \dfrac{1}{2\pi j} \int_{\sigma_1 - j\infty}^{\sigma_1 + j \infty} F(s) e^{st} ds \nonumber \]
El par de transformación directo-inversa es único (Hay tres restricciones adicionales llamadas condiciones Direchlet que se satisfacen para todas las señales de origen físico. El lector interesado es referido a Gardner y Barnes.) para que
\[\mathcal{L}^{-1} \mathcal{L} [f(t)] = f(t)\label{eq3.2.3} \]
si\(f(t) = 0\),\(t < 0\), y si\(\int_{0}^{\infty} |f(t)| e^{-\sigma_1 t} dt\) es finito para algún valor real de\(\sigma_1\).
Una serie de teoremas útiles para el análisis de sistemas dinámicos pueden ser desarrollados a partir de las definiciones de las transformaciones directas e inversas para funciones que satisfacen las condiciones de Ecuación\(\ref{eq3.2.3}\). Entre los más importantes de estos teoremas se encuentran los siguientes.
- Linealidad
\[\mathcal{L} [af(t) + bg(t)] = [aF(s) + bG(s)]\nonumber \]
donde\(a\) y\(b\) son constantes. - Diferenciación
\[\mathcal{L} \left [\dfrac{df(t)}{dt} \right ] = sF(s) - \lim_{t \to 0^+} f(t) \nonumber \]
(El límite se toma acercándose\(t = 0\) de positivo\(t\).) - Integración
\[\mathcal{L} \left [\int_{0}^{t} f(\tau) d\tau \right ] = \dfrac{F(s)}{s}\nonumber \] - Convolución
\[\mathcal{L} \left [\int_{0}^{t} f(\tau) g(t - \tau) d\tau \right ] = \mathcal{L} \left [\int_{0}^{t} f(t - \tau) g(\tau) d \tau \right ] = F(s) G(s) \nonumber \] - Cambio de tiempo
\[\mathcal{L} [ f(t - \tau)] = F(s) e^{-s\tau}\nonumber \]
si es\(f(t - \tau) = 0\) para\((t - \tau) < 0\), donde\(\tau\) es una constante positiva. - Escala de tiempo
\[\mathcal{L} [f(at)] = \dfrac{1}{a} F \left [\dfrac{s}{a} \right ]\nonumber \]
donde\(a\) es una constante positiva. - Valor inicial
\[\lim_{t \to 0^+} f(t) = \lim_{s \to \infty} sF(s)\nonumber \] - Valor final
\[\lim_{t \to \infty} f(t) = \lim_{s \to 0} sF(s)\nonumber \]
El teorema 4 es particularmente valioso para el análisis de sistemas lineales, ya que muestra que la transformada de Laplace de una salida de sistema es el producto de la transformación de la señal de entrada y la transformación de la respuesta de impulso del sistema.
Transformas de funciones comunes
Las integrales definitorias siempre se pueden utilizar para convertir de una función de tiempo a su transformación o viceversa. En la práctica, los valores tabulados se utilizan frecuentemente por conveniencia, y muchas referencias matemáticas o de ingeniería (Ver, por ejemplo, A. Erdeyli (Editor) Tables of Integrales Transforms, Vol. 1, Bateman Manuscript Project, McGraw-Hill, Nueva York, 1954 y R. E. Boly y G. L. Tuve, (Editores), Handbook of Tables for Applied Engineering Science, The Chemical Rubber Company, Cleveland, 1970.) contienen listas extensas de funciones de tiempo y transformaciones correspondientes de Laplace. En la Tabla 3.1 se presenta una breve lista de las transformaciones de Laplace.
Las funciones de tiempo correspondientes a proporciones de polinomios en\(s\) que no se listan en la tabla pueden evaluarse mediante una expansión parcial de la fracción. La función de interés está escrita en la forma
\[F(s) = \dfrac{p(s)}{q(s)} = \dfrac{p(s)}{(s + s_1)(s + s_2) \cdots (s + s_n)} \nonumber \]
Se supone que el orden del polinomio numerador es menor que el del denominador. Si todas las raíces del polinomio denominador son de primer orden (es decir,\(s_i \ne s_j\),\(i \ne j\)),
\[F(s) = \sum_{k = 1}^{n} \dfrac{A_k}{s + s_k} \label{eq3.2.5} \]
donde
\[A_k = \lim_{s \to -s_k} [(s + s_k) F(s)] \label{eq3.2.6} \]
Si una o más raíces del polinomio denominador son raíces múltiples, aportan términos de la forma
\[\sum_{k = 1}^{m} \dfrac{B_k}{(s + s_i)^k} \label{eq3.2.7} \]
Tabla 3.1 Pares de Transformación de Laplace
| \(F(s)\) | \(f(t), t \ge 0\) \([f(t) = 0, t < 0]\) |
| 1 | Impulso unitario\(u_0 (t)\) |
| \(\dfrac{1}{s}\) | Paso de unidad\(u_{-1} (t)\) \([f(t) = 1, t \ge 0]\) |
| \(\dfrac{1}{s^2}\) | Paso de unidad\(u_{-2} (t)\) \([f(t) = 1, t \ge 0]\) |
| \(\dfrac{1}{s^{n + 1}}\) | \(\dfrac{t^n}{n!}\) |
| \(\dfrac{1}{s + a}\) | \(e^{-at}\) |
| \(\dfrac{1}{(s + a)^{n + 1}}\) | \(\dfrac{t^n}{(n)!} e^{-at}\) |
| \(\dfrac{1}{s(\tau s + 1)}\) | \(1 - e^{-t/\tau}\) |
| \(\dfrac{\omega}{(s + a)^2 + \omega^2}\) | \(e^{-at} \sin \omega t\) |
| \(\dfrac{s + a}{(s + a)^2 + \omega^2}\) | \(e^{-at} \cos \omega t\) |
| \(\dfrac{1}{s^2/\omega_n^2 + 2 \zeta s/\omega_n + 1}\) | \(\dfrac{\omega_n}{\sqrt{1 - \zeta^2}} e^{-\zeta \omega_n t} (\sin \omega_n \sqrt{1 - \zeta^2} t), \zeta < 1\) |
| \(\dfrac{1}{s(s^2/\omega_n^2 + 2 \zeta s/\omega_n + 1)}\) | \(1 - \dfrac{e^{-zeta \omega_n t}}{\sqrt{1 - \zeta^2}} \sin \left [\omega_n \sqrt{1 - \zeta^2} t + \tan^{-1} \left (\dfrac{\sqrt{1 - \zeta^2}}{\zeta} \right ) \right ], \zeta < 1\) |
donde\(m\) es el orden de la raíz múltiple ubicada en\(s = -s_i\). Los\(B\)'s se determinan a partir de la relación
\[B_k = \lim_{s \to -s_i} \left \{\dfrac{1}{(m - k)!} \dfrac{d^{m-k}}{ds^{m - k}} [(s + s_i)^m F(s)] \right \} \label{eq3.2.8} \]
Debido a la propiedad de linealidad de Laplace transforma, es posible encontrar la función de tiempo\(f(t)\) sumando las contribuciones de todos los componentes de\(F(s)\).
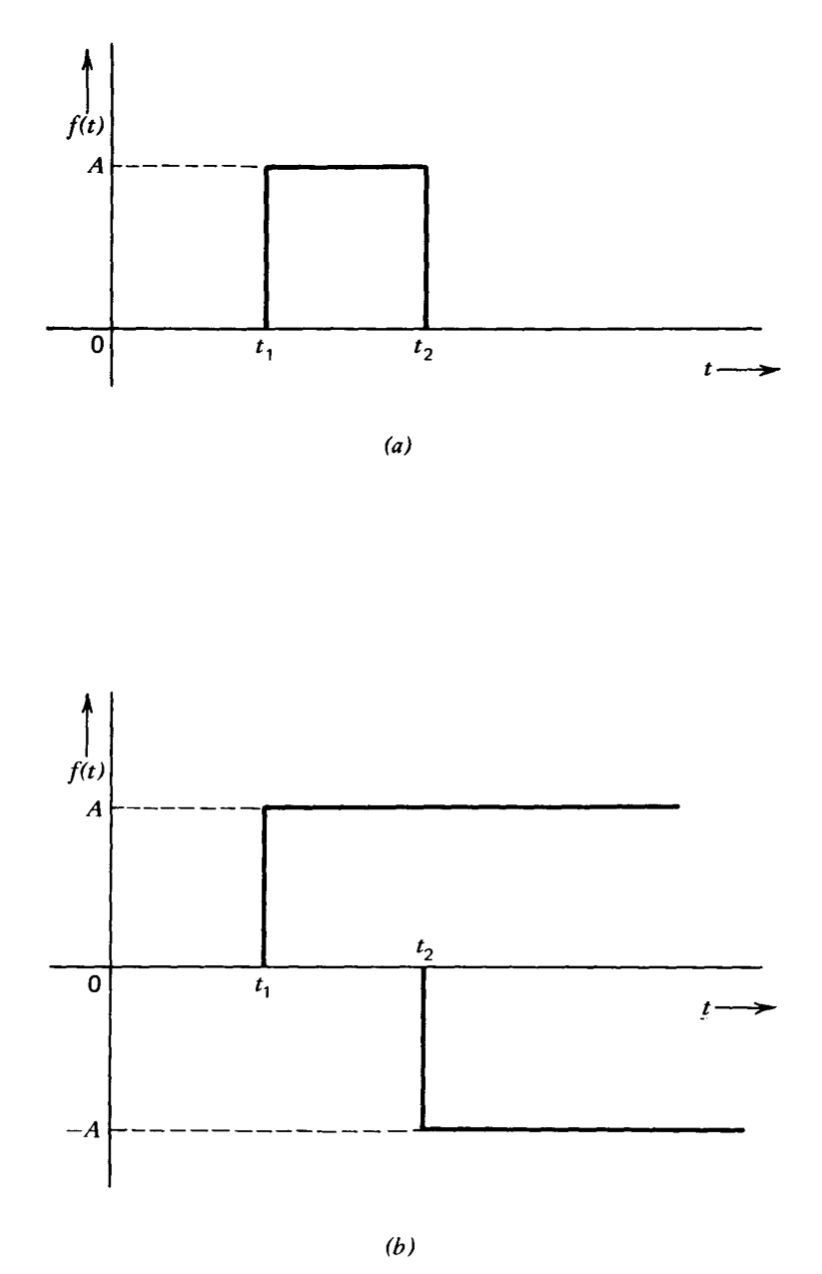
Las propiedades de las transformaciones de Laplace enumeradas anteriormente a menudo se pueden usar para determinar la transformación de funciones de tiempo que no aparecen en la tabla. El pulso rectangular mostrado en la Figura 3.3 proporciona un ejemplo de esta técnica. El pulso (Figura 3.3a) se puede descomponer en dos pasos, uno con una amplitud de\(+A\) inicio en\(t = t_1\), sumado con un segundo paso de amplitud\(-A\) comenzando en\(t = t_2\). Los teoremas 1 y 5 combinados con la transformación de un paso unitario de la Tabla 3.1 muestran que la transformación de un paso con amplitud\(A\) que comienza en\(t = t_1\) es\((A/s)e^{-st_1}\). De igual manera, la transformación del segundo componente es\(-(A/s) e^{-st_2}\). La superposición asegura que la transformación de\(f(t)\) es la suma de estas dos funciones, o
\[F(s) = \dfrac{A}{s} (e^{-st_1} - e^{-st_2}) \nonumber \]
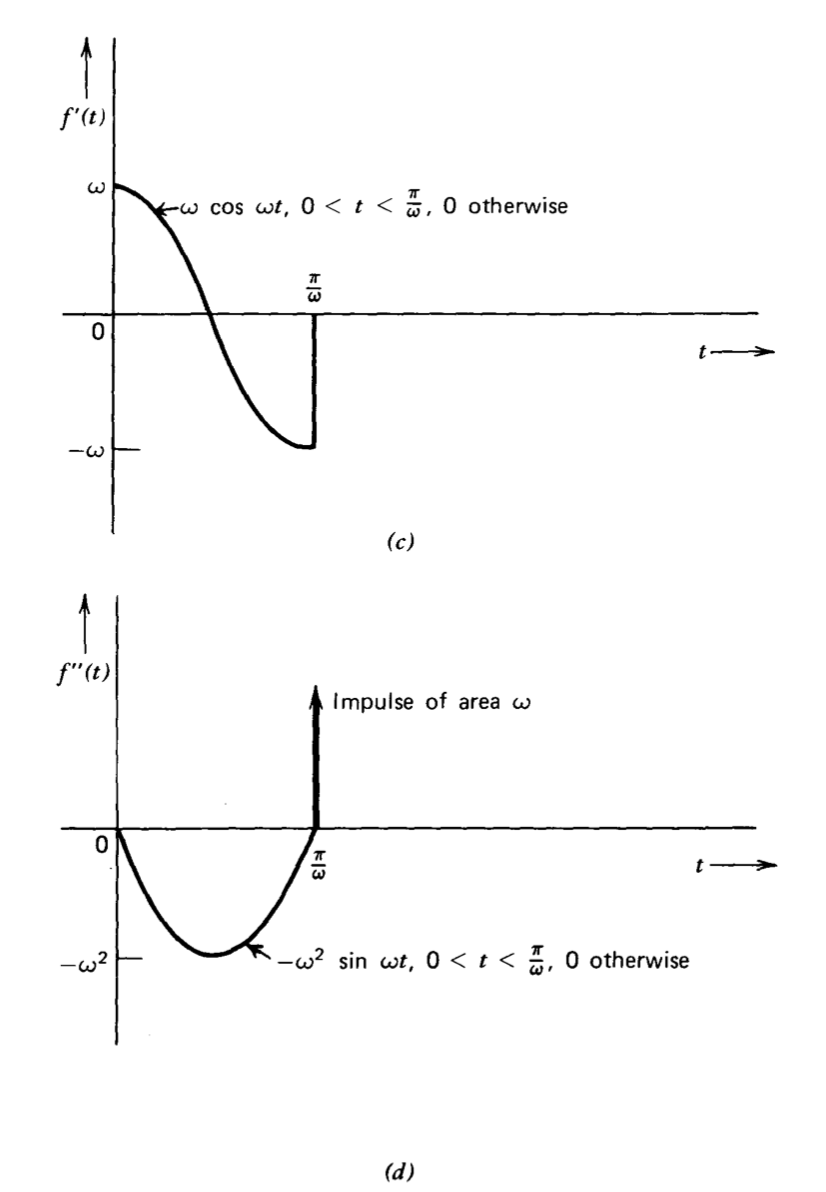
El pulso sinusoidal mostrado en la Figura 3.4 se utiliza como segundo ejemplo. Un enfoque es representar el pulso único como la suma de dos sinusoides exactamente como se hizo para el pulso rectangular. El Cuadro 3.1 muestra que la transformación de una sinusoide de amplitud unitaria que comienza en el tiempo\(t = 0\) es\(\omega/ (s^2 + \omega^2)\). Sumar transformadas de los componentes mostrados en la Figura 3.4\(b\) rendimientos
\[F(s) = \dfrac{\omega}{s^2 + \omega^2} [1 + e^{-s(\tau /\omega)}] \nonumber \]
Un enfoque alternativo implica diferenciar\(f(t)\) dos veces. La derivada de\(f(t)\),\(f'(t)\), se muestra en la Figura 3.4\(c\). Ya que\(f(0) = 0\), el teorema 2 muestra que
\[\mathcal{L} [f'(t)] = sF(s) \nonumber \]
La segunda derivada de\(f(t)\) se muestra en la Figura 3.4\(d\). Aplicación del teorema 2 a esta función (La porción de esta expresión implicada\(\lim t \to 0^+\) podría eliminarse si se\(\omega u_0 (t)\) incluyera un segundo impulso en\(f''(t)\).) conduce a
\[\mathcal{L} [f'' (t)] = s \mathcal{L} [f'(t)] - \lim_{t \to 0^+} f'(t) = s^2 F(s) - \omega \label{eq3.2.12} \]
Sin embargo, la Figura 3.4\(d\) indica que
\[f''(t) = -\omega^2 f(t) + \omega u_0 \left (t - \dfrac{\pi}{\omega} \right ) \nonumber \]
Así
\[\mathcal{L} [f'' (t)] = -\omega^2 F(s) + \omega e^{-s(\pi/\omega)} \label{eq3.2.14} \]
Combinación de ecuaciones\(\ref{eq3.2.12}\) y\(\ref{eq3.2.14}\) rendimientos
\[s^2 F(s) - \omega = -\omega^2 F(s) + \omega e^{-s (\pi/\omega)} \label{eq3.2.15} \]
Ecuación\(\ref{eq3.2.15}\) se resuelve para\(F(s)\) con el resultado de que
\[F(s) = \dfrac{\omega}{s^2 + \omega^2} [1 + e^{-s (\pi/ \omega)}] \nonumber \]
Obsérvese que este desarrollo, en contraste con el que implica superposición, no se basa en el conocimiento de la transformación de una sinusoide, e incluso puede ser utilizado para determinar esta transformación.
Ejemplos del uso de las transformadas
Las transformaciones de Laplace ofrecen un método conveniente para la solución de ecuaciones diferenciales lineales invariables en el tiempo, ya que reemplazan la integración y diferenciación requerida para resolver estas ecuaciones en el dominio del tiempo por manipulación algebraica. Como ejemplo, considere la ecuación diferencial
\[\dfrac{d^2 x}{dt^2} + 3 \dfrac{dx}{dt} + 3x = e^{-t} \ \ t > 0 \label{eq3.2.17} \]
sujeto a las condiciones iniciales
\[x(0^+) = 2 \ \ \ \dfrac{dx}{dt} (0^+) = 0 \nonumber \]
La transformación de ambos lados de la Ecuación\(\ref{eq3.2.17}\) se toma utilizando el teorema 2 (aplicado dos veces en el caso de la segunda derivada) y el Cuadro 3.1 para determinar la transformada de Laplace de\(e^{-t}\).
\[s^2 X(s) - sx (0^+) - \dfrac{dx}{dt} (0^+) + 3sX(s) - 3x (0^+) + 2X(s) = \dfrac{1}{s + 1} \nonumber \]
Recopilación de términos y resolución de\(X(s)\) rendimientos
\[X(s) = \dfrac{2s^2 + 8s + 7}{(s + 1)^2 (s + 2)} \nonumber \]
Ecuaciones\(\ref{eq3.2.5}\) y\(\ref{eq3.2.7}\) muestran que como hay una raíz de primer orden y una raíz de segundo orden,
\[X(s) = \dfrac{A_1}{(s + 2)} + \dfrac{B_1}{(s + 1)} + \dfrac{B_2}{(s + 1)^2} \nonumber \]
Los coeficientes se evalúan con la ayuda de Ecuaciones\(\ref{eq3.2.6}\) y\(\ref{eq3.2.8}\), con el resultado de que
\[X(s) = \dfrac{-1}{s + 2} + \dfrac{3}{s + 1} + \dfrac{1}{(s + 1)^2} \nonumber \]
La transformación inversa de\(X(s)\), evaluada con la ayuda del Cuadro 3.1, es
\[x(t) = -e^{-2t} + 3e^{-t} + te^{-t} \nonumber \]
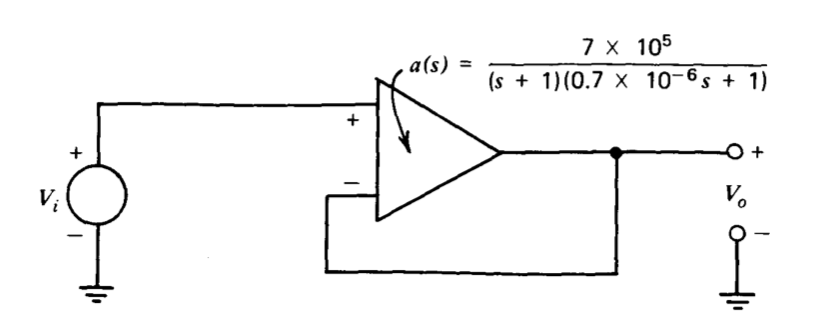
El amplificador operacional conectado como un amplificador no inversor de ganancia de unidad (Figura 3.5) se utiliza como un segundo ejemplo que ilustra las técnicas de Laplace. Si asumimos que la carga es insignificante,
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{a(s)}{1 + a(s)} = \dfrac{7 \times 10^5}{(s + 1)(0.7 \times 10^{-6} s + 1) + 7 \times 10^5} \simeq \dfrac{1}{10^{-12} s^2 + 1.4 \times 10^{-6} s + 1} \nonumber \]
Si la señal de entrada es un paso de unidad\(1/s\),\(V_i (s)\) es decir,
\[V_o (s) = \dfrac{1}{s (10^{-12} s^2 + 1.4 \times 10^{-6} s + 1)} = \dfrac{1}{s[s^2/(10^6)^2 + 2(0.7)s/10^6 + 1]}\label{eq3.2.24} \]
El término final en Ecuación\(\ref{eq3.2.24}\) muestra que la porción cuadrática de la expresión tiene una frecuencia natural\(\omega_n = 10^6\) y una relación de amortiguación\(\zeta = 0.7\). La función de tiempo correspondiente se determina a partir de la Tabla 3.1, con el resultado
\[f(t) = 1 - \dfrac{e^{-0.7 \times 10^6 t}}{0.7} \sin (0.7 \times 10^6 t + 45^{\circ}) \nonumber \]


