4.4: Estabilidad basada en la respuesta de frecuencia
- Page ID
- 84109
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El criterio Routh y los métodos de locus raíz proporcionan información sobre la estabilidad de un sistema de retroalimentación a partir de la ecuación característica o las singularidades de transmisión de bucle del sistema. Por lo tanto, ambas técnicas requieren que la transmisión en bucle del sistema sea expresable como una relación de polinomios en\(s\). Hay dos posibles dificultades. El sistema puede incluir elementos con funciones de transferencia que no pueden expresarse como una relación de polinomios finitos. Un ejemplo familiar de este tipo de elemento es el retardo de tiempo puro de\(\tau\) segundos con una función de transferencia\(e^{-s\tau}\). Una segunda posibilidad es que la información disponible sobre el sistema consista en una respuesta de frecuencia determinada experimentalmente. La aproximación de los datos medidos en una forma adecuada para el análisis de Routh o de locus radicular puede no ser práctico.
Los métodos descritos en esta sección evalúan la estabilidad de un sistema de retroalimentación a partir de su transmisión en bucle en función de la frecuencia. Los únicos datos requeridos son la magnitud y el ángulo de esta transmisión, y no es necesario que estos datos se presenten como expresiones analíticas. Como resultado, la estabilidad se puede determinar directamente a partir de los resultados experimentales.
Criterio Nyquist
Es necesario desarrollar un método para determinar la información de estabilidad absoluta y relativa para los sistemas de retroalimentación basado en la variación de sus transmisiones de bucle con frecuencia. Se asume la topología de la Figura 4.1. Si hay alguna frecuencia\(\omega\) a la que
\[a(j \omega) f(j \omega) = -1 \nonumber \]
la transmisión en bucle es + 1 a esta frecuencia. Es evidente que el sistema puede entonces oscilar a la frecuencia co, ya que en efecto puede suministrar su propia señal de accionamiento sin una entrada aplicada externamente. Este tipo de argumento intuitivo falla en muchos casos de interés práctico. Por ejemplo, un sistema con una transmisión en bucle de +10 a alguna frecuencia puede o no ser
estable dependiendo de los valores de transmisión de bucle en otras frecuencias. El criterio Nyquist puede ser utilizado para resolver esta y otras cuestiones de estabilidad. La prueba determina si hay algún valor de s con partes reales positivas para las cuales\(a(s)f(s) = -1\). Si se cumple esta condición, la ecuación característica del sistema tiene un cero de medio plano derecho que implica inestabilidad. Para utilizar el criterio Nyquist, la función\(a(s)f(s)\) se evalúa como s toma valores a lo largo del contorno mostrado en la gráfica\(s\) -plano de la Figura 4.16. El contorno incluye un segmento del eje imaginario y se cierra con un gran semicírculo de radio\(R\) que se encuentra en la mitad derecha del\(s\) plano. Los valores de\(a(s)f(s)\) como\(s\) varía a lo largo del contorno indicado se trazan en forma de fase de ganancia en un plano af. En la Figura 4.17 se muestra una posible gráfica de\(af\) plano. La simetría sobre la\(0^{\circ}\) línea en el\(af\) plano es característica de todas esas parcelas desde entonces\(\text{Im} [a(j\omega )f(j\omega )] = - \text{Im} [a(-j\omega )f(-j\omega)]\).
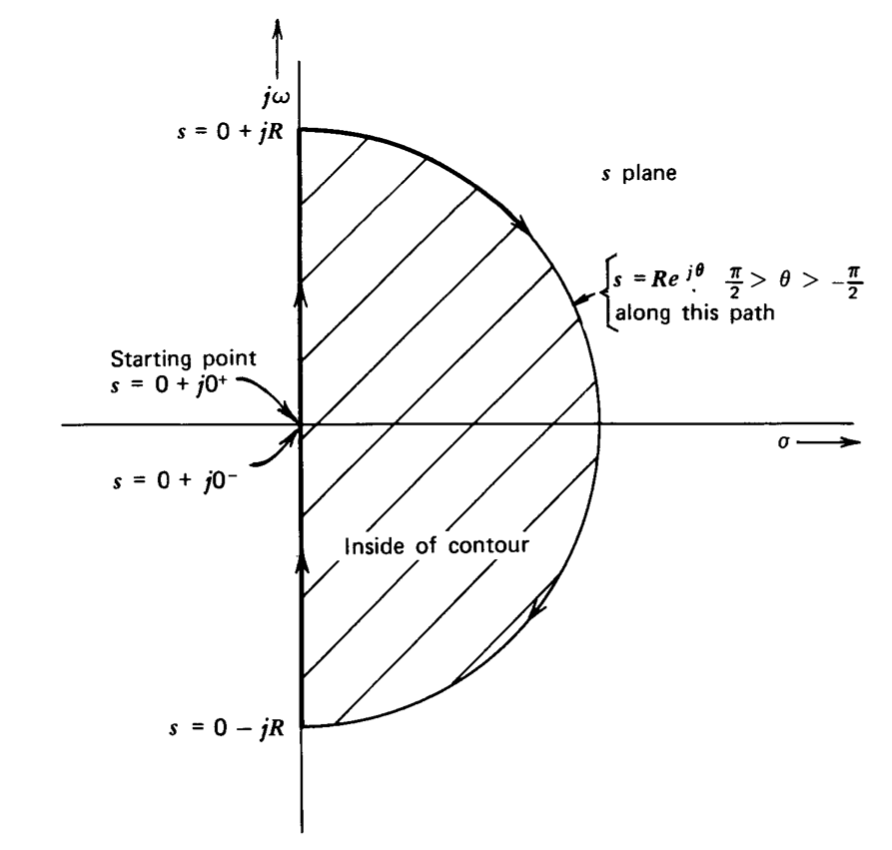
Figura 4.16 Contorno Se utiliza para evaluar\(a(s) f(s)\).
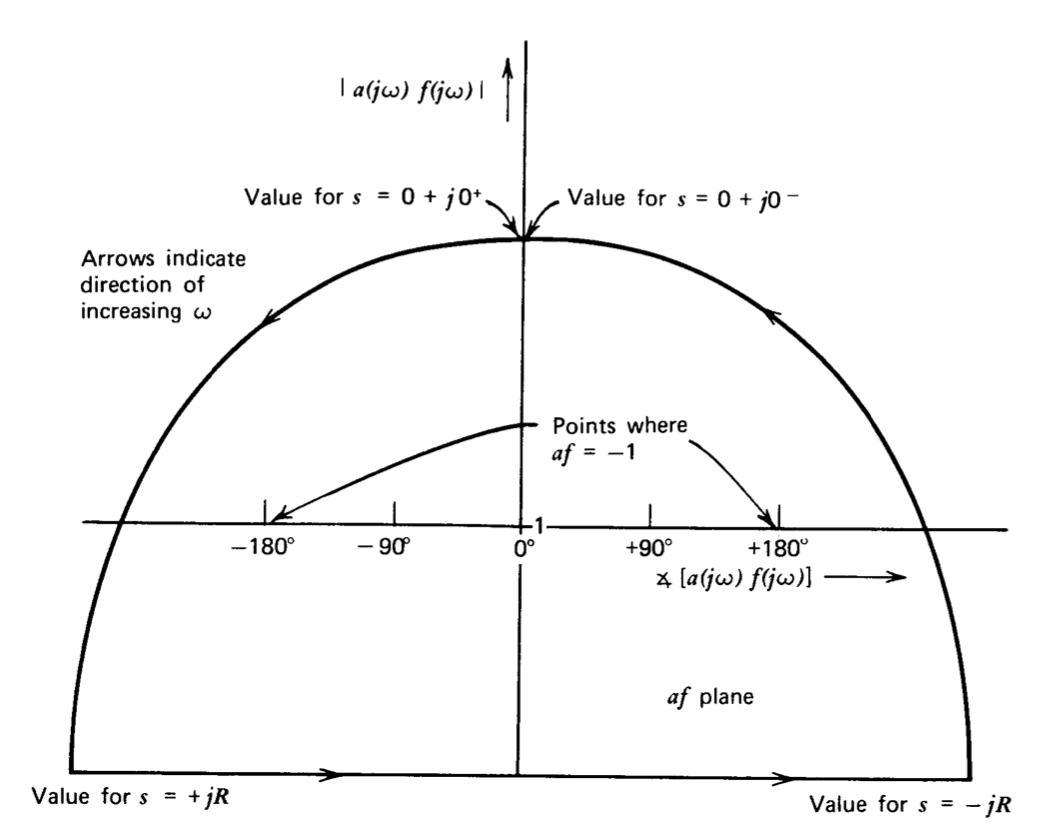
Figura 4.17 Gráfica de\(a(s) f(s)\) como\(s\) varía a lo largo del contorno de la Figura 4.16.
Nuestro objetivo es determinar si existen valores de\(s\) que se encuentran en la región sombreada de la Figura 4.16 para la cual\(a(s)f(s) = - 1\). Esta determinación se simplifica al reconocer que la transformación involucrada mapea contornos cerrados en el\(s\) plano en contornos cerrados en el\(af\) plano. Además,
todos los valores de\(s\) ese se encuentran en un lado de un contorno en el\(s\) plano deben mapearse a valores de\(af\) que se encuentran en un lado del contorno correspondiente en el\(af\) plano. Los puntos - 1 están claramente indicados en la gráfica\(af\) -plano. Así, la única tarea restante es determinar si la región sombreada en la Figura 4.16 se mapea al interior o al exterior del contorno en la Figura 4.17. Si mapea hacia el interior, hay dos valores de\(s\) en el plano de la mitad derecha para los cuales\(a(s)f(s) = -1\), y el sistema es inestable.
La forma de la gráfica\(af\) -plano y las regiones correspondientes de las dos parcelas se determinan fácilmente a partir de\(a(s)f(s)\) como se ilustra en los siguientes ejemplos. La Figura 4.18 indica la forma general de las gráficas\(s\) -plano y\(af\) -plano para
\[a(s) f(s) = \dfrac{10^3}{(s + 1)(0.1s + 1)(0.01s + 1)} \nonumber \]
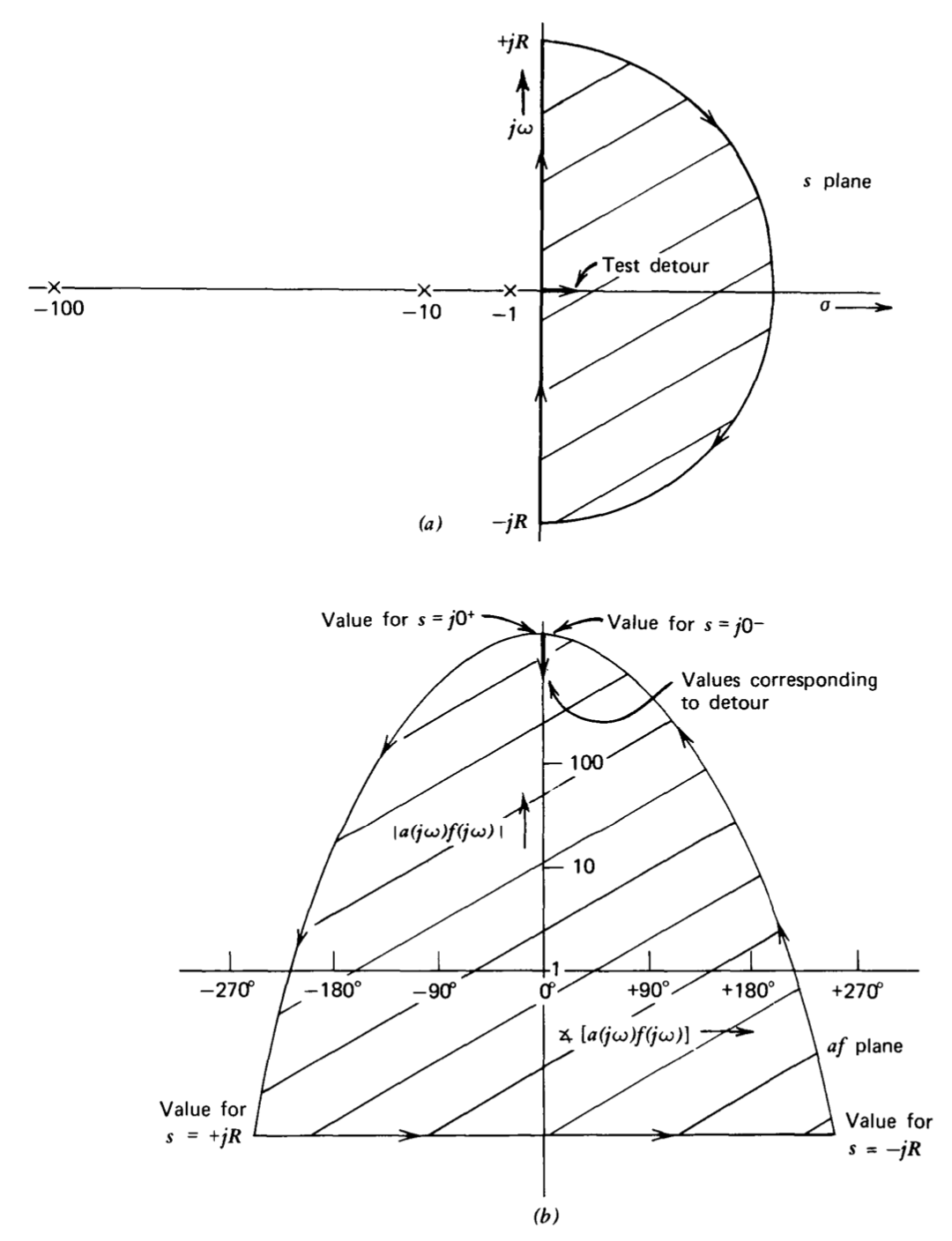
Obsérvese que la magnitud de\(af\) en este ejemplo es\(10^3\) y su ángulo es cero en\(s = 0\). A medida que\(s\) adquiere valores que se acercan a +\(jR\), el ángulo de\(af\) los cambios de 0' hacia\(-270^{\circ}\), y su magnitud disminuye. Estas relaciones se obtienen fácilmente a partir de las manipulaciones vectoriales habituales en el\(s\) plano. Para un valor suficientemente grande de\(R\), la magnitud de af es arbitrariamente pequeña, y su ángulo es casi\(-270^{\circ}\). Como s asume valores en el plano medio derecho a lo largo de un semicírculo de radio\(R\), la magnitud de\(af\) permanece constante (para\(R\) mucho mayor que la distancia de cualquier singularidad de af desde el origen), y su ángulo cambia de\(-270^{\circ}\) a\(0^{\circ}\) como\(s\) va de + \(jR\)a +\(R\). El resto de la gráfica\(af\) -plane debe ser simétrico alrededor de la\(0^{\circ}\) línea.
Para mostrar que las dos regiones sombreadas se corresponden entre sí, se realiza un pequeño desvío del contorno en el\(s\) plano\(s = 0\) como se indica en la Figura 4.18\(a\). A medida que s asume valores positivos reales, la magnitud de\(a(s)f(s)\) disminuye, ya que la distancia desde el punto en el desvío de prueba a cada uno de los polos aumenta. Así, el desvío produce valores en el\(af\) plano que se encuentran en la región sombreada. Si bien normalmente utilizaremos un desvío de prueba para determinar las regiones correspondientes en los dos planos, las relaciones angulares indicadas en este ejemplo son generales. Debido a la forma en que se eligen los ejes en los dos planos, los giros a la derecha en un plano mapean a los giros a la izquierda en el otro. Una consecuencia de esta inversión se ilustra en la Figura 4.18. Tenga en cuenta que si seguimos el contorno en el\(s\) plano en dirección a las flechas, la región sombreada está a nuestra derecha. La inversión de ángulo coloca la región correspondiente en el plano af a la izquierda cuando se sigue su límite en la dirección de las flechas.
Dado que los dos - 1 puntos se encuentran en la región sombreada del plano af, hay dos valores de\(s\) en el plano de la mitad derecha para lo cual\(a(s)f(s) = - 1\) y el sistema es inestable. Tenga en cuenta que si\(a_0f_0\) se reduce, el contorno en el plano af se desliza hacia abajo y para valores suficientemente pequeños\(a_0f_0\) del sistema es estable. Un desarrollo geométrico o el criterio de Routh muestra que el sistema es estable para valores positivos\(a_0f_0\) menores a 122.21.
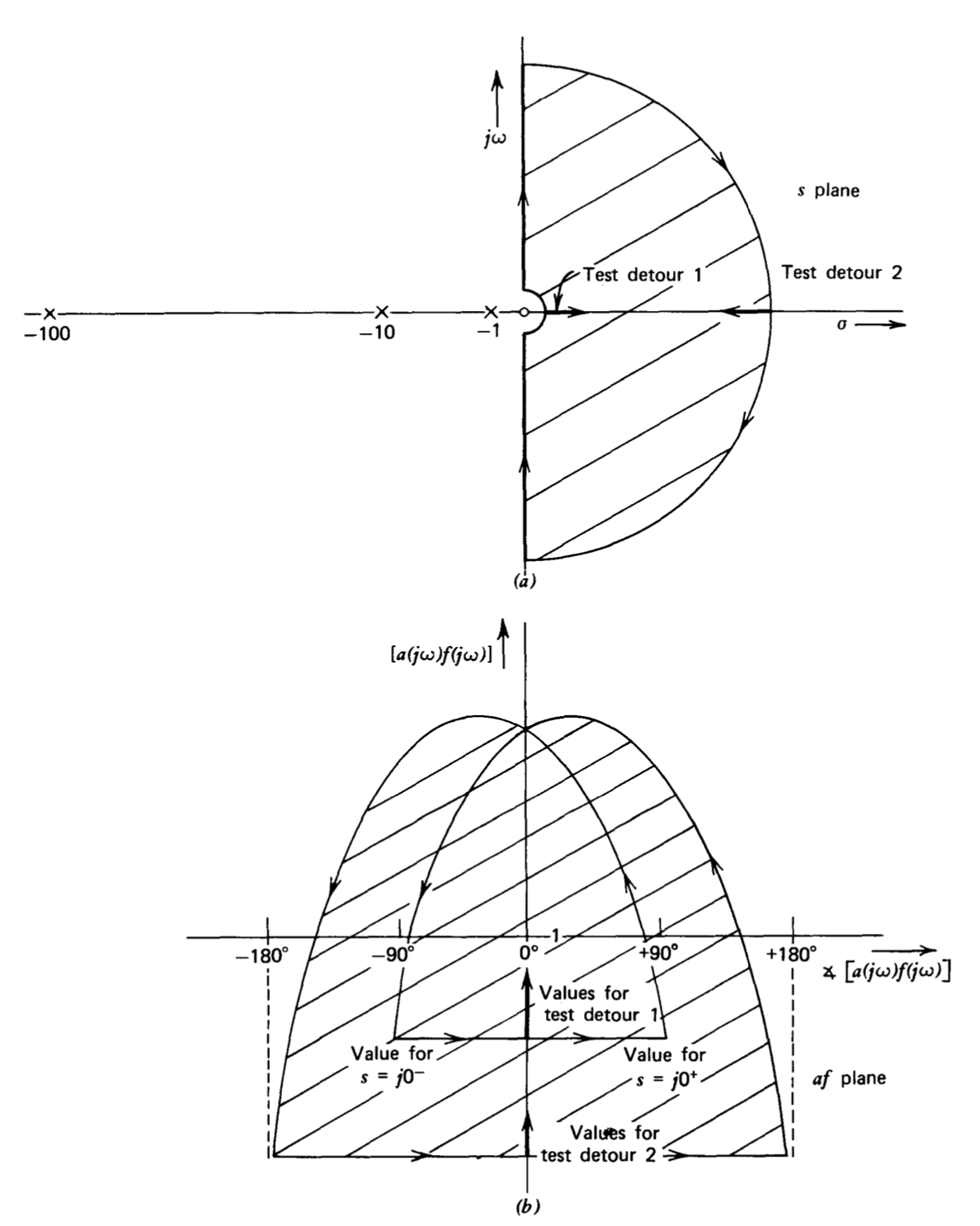
Los contornos con la forma general mostrada en la Figura 4.19 resultan si se agrega un cero en el origen cambiando\(a(s)f(s)\) a
\[a(s) f(s) = \dfrac{10^3 s}{(s + 1)(0.1s + 1)(0.01s + 1)} \nonumber \]
Para evitar incertidumbres de ángulo y magnitud que resultan si el contorno del plano s pasa por una singularidad, se utiliza un arco circular de radio pequeño para evitar el cero. Se muestran dos desvíos de prueba en el contorno del plano S. A medida que se sigue el primero, la magnitud de af aumenta ya que el efecto dominante es el de dejar el cero. A medida que se sigue el segundo desvío de prueba, la magnitud de los\(af\) aumentos ya que este desvío se acerca a tres polos y sólo uno cero. La ubicación de la región sombreada en el\(af\) plano indica que los puntos -1 permanecen fuera de esta región para todos los valores positivos de\(a_0\) y, por lo tanto, el sistema es estable para cualquier cantidad de retroalimentación negativa.
La prueba Nyquist también se puede utilizar para sistemas que tienen uno o más polos de transmisión de bucle en el plano de la mitad derecha y, por lo tanto, son inestables sin retroalimentación. Un ejemplo de este tipo de sistema resulta para
\[a(s) f(s) = \dfrac{a_0}{s - 1} \nonumber \]
con las gráficas\(s\) -plano y\(af\) -plano mostradas en las Figs. 4.20\(a\) y 4.20\(b\). La línea indicada por + marcas en la gráfica\(af\) -plano es un intento de mostrar que para este sistema el ángulo debe ser continuo a medida que\(s\) cambia de\(j0^-\) a\(j0^+\). Para preservar esta necesaria continuidad, debemos darnos cuenta de que\(+180^{\circ}\) y\(-180^{\circ}\) son ángulos idénticos, y concebir el plano af como un cilindro unido en las\(\pm 180^{\circ}\) líneas. Este concepto se hace algo menos perturbador mediante el uso de coordenadas polares para la gráfica\(af\) -plano como se muestra en la Figura 4.20\(c\). Aquí el punto -1 aparece sólo una vez. El uso del desvío de prueba muestra que los valores de\(s\) en el plano de la mitad derecha se mapean fuera de un círculo que se extiende desde 0 hasta\(-a_0\) como se muestra en la Figura\(c\) 4.20. La ubicación del punto - 1 en cualquiera de las gráficas de plano af muestra que el sistema es estable solo para\(a_0 > 1\).
Tenga en cuenta que los - 1 puntos en el\(af\) plano correspondientes a los ángulos de\(\pm 180^{\circ}\) colapso a un punto cuando se forma el cilindro af necesario para la construcción Nyquist para este ejemplo. Esta característica y la naturaleza del contorno af muestran que cuando\(a_0\) es menor de uno, solo hay un valor\(s\) para el cual\(a(s)f(s) = - 1\). Por lo tanto, este sistema tiene un solo polo de bucle cerrado en el eje real positivo para valores de\(a_0\) ese resultado en inestabilidad.
Este sistema indica otro tipo de dificultad que se puede encontrar con sistemas que tienen singularidades de transmisión de bucle de medio plano derecho. El ángulo de\(a(j\omega )f(j\omega )\) es\(180^{\circ}\) a bajas frecuencias, lo que implica que el sistema realmente tiene retroalimentación positiva en estas frecuencias. (Recordemos la inversión adicional incluida en el punto de suma en nuestra representación estándar). La representación del plano s (Figura 4.20\(a\)) es consistente ya que indica un ángulo de\(180^{\circ}\) for\(s = 0\). Por lo tanto, en este caso no es necesaria ninguna modificación procesal del tipo de trazado en la Sección 4.3.3.
Interpretación de parcelas de Bode
Una gráfica de Bode no contiene la información relativa a los valores de af ya que el contorno en el\(s\) plano está cerrado, lo cual es necesario para aplicar la prueba de Nyquist. La experiencia demuestra que la forma más fácil de determinar la estabilidad
a partir de una gráfica de Bode de una transmisión de bucle arbitraria es esbozar aproximadamente una gráfica\(af\) de plano completo y aplicar la prueba de Nyquist como se describe en la Sección 4.4.1. Para muchos sistemas de interés práctico, sin embargo, es posible eludir este paso y utilizar la información de Bode directamente.
Las siguientes dos reglas evolucionan a partir de la prueba de Nyquist para sistemas que tienen retroalimentación negativa a frecuencias bajas o medias y que no tienen singularidades de medio plano derecho en su transmisión de bucle.
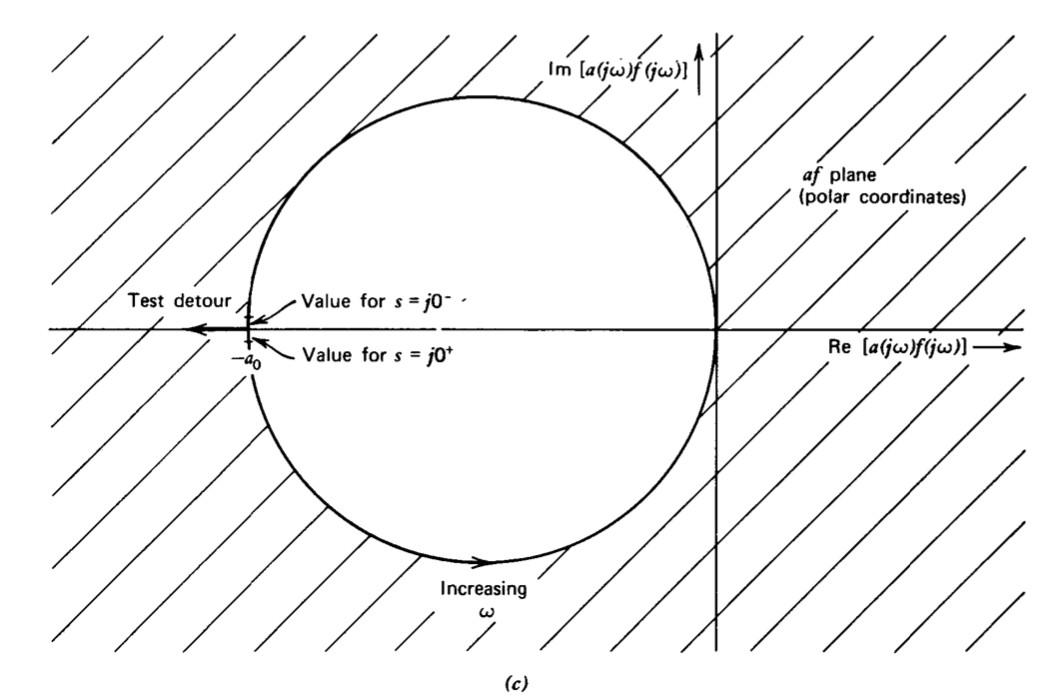
- Si la magnitud de af es 1 a una sola frecuencia, el sistema es estable si el ángulo de\(af\) está entre\(+180^{\circ}\) y\(-180^{\circ}\) en la frecuencia de ganancia unitaria.
- Si el ángulo de af pasa a través\(+180^{\circ}\) o\(-180^{\circ}\) a una sola frecuencia, el sistema es estable si la magnitud de af es menor que 1 en esta frecuencia.
La información sobre la estabilidad relativa de un sistema de retroalimentación también se puede determinar a partir de una gráfica de Bode por la siguiente razón. Los valores de\(s\) para los cuales\(af = - 1\) son las ubicaciones de polos de bucle cerrado de un sistema de retroalimentación. La prueba de Nyquist explota esta relación para determinar la estabilidad absoluta de un sistema. Si el sistema es estable, pero se\(af\) producen un par de -1 para valores de s cercanos al eje imaginario, el sistema debe tener un par de polos de bucle cerrado con una pequeña relación de amortiguación.
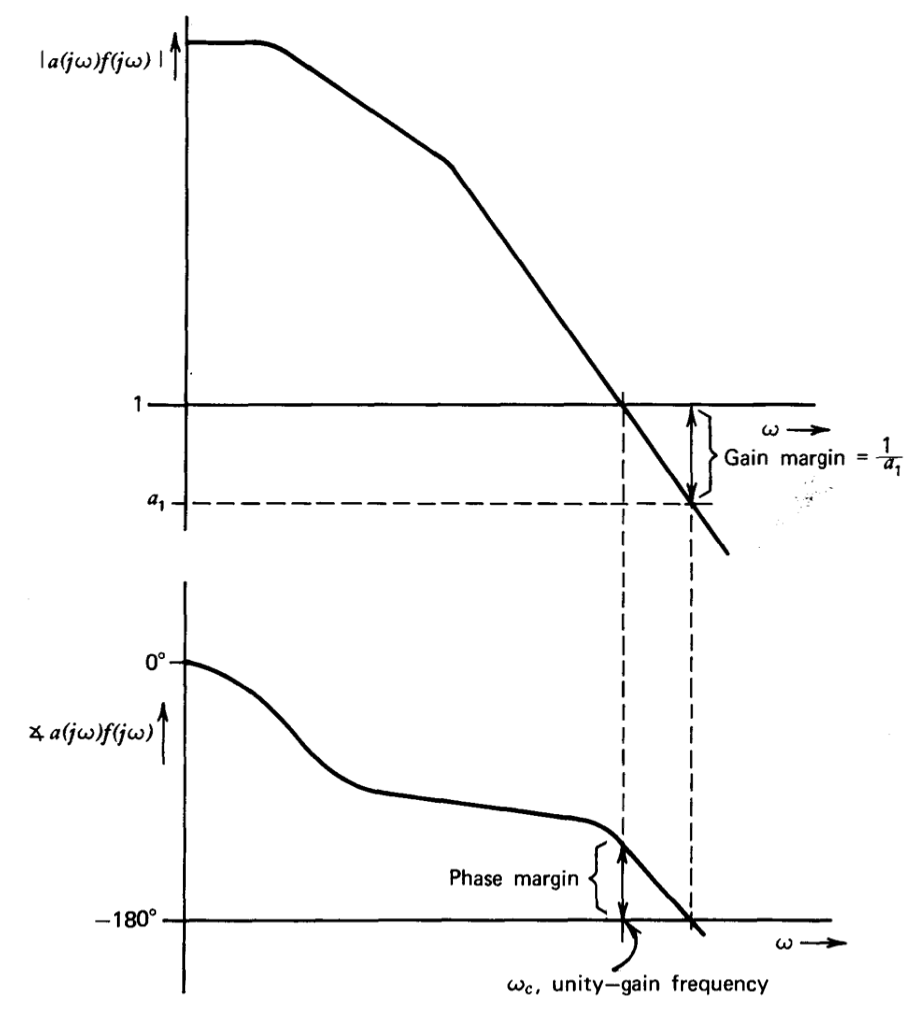
Las cantidades mostradas en la Figura 4.21 proporcionan una estimación útil de la proximidad de -1's\(af\) al eje imaginario y así indican estabilidad relativa. El margen de fase es la diferencia entre el ángulo de af y\(-180^{\circ}\) a la frecuencia donde la magnitud de af es 1. Un margen de fase\(0^{\circ}\) indica polos de bucle cerrado en el eje imaignary y, por lo tanto, el margen de fase es una medida del desplazamiento de fase negativo adicional en la frecuencia de magnitud unitaria que causará inestabilidad. Del mismo modo, el margen de ganancia es la cantidad de aumento de ganancia requerida para hacer la magnitud de la\(af\) unidad a la frecuencia donde\(af\) se encuentra el ángulo de\(-180^{\circ}\), y representa la
cantidad de incremento en\(a_0f_0\) requerido para causar inestabilidad. La frecuencia a la que la magnitud de\(af\) es unidad se denomina frecuencia de ganancia de unidad o frecuencia de cruce. Este parámetro caracteriza la respuesta de frecuencia relativa o la velocidad de la respuesta de tiempo del sistema.
Una característica particularmente valiosa del análisis basado en las características de transmisión de bucle de un sistema es que el margen de ganancia y el margen de fase, cantidades que se determinan rápida y fácilmente mediante técnicas de Bode, dan sorprendentemente buenos indicios de la estabilidad relativa de un sistema de retroalimentación. Generalmente se encuentra que los márgenes de ganancia de tres o más combinados con márgenes de fase entre 30 y\(60^{\circ}\) resultan en compensaciones deseables entre ancho de banda o tiempo de subida y estabilidad relativa. Los valores más pequeños para ganancia y margen de fase corresponden a una menor estabilidad relativa y se evitan si es necesario un pequeño sobreimpulso en respuesta a un escalón o un pequeño pico de frecuencia-respuesta o si existe la posibilidad de cambios severos en los valores de los parámetros.
El ancho de banda de bucle cerrado y el tiempo de subida están relacionados casi directamente con la frecuencia de ganancia unitaria para sistemas con márgenes de ganancia y fase iguales. Por lo tanto, cualquier cambio que aumente la frecuencia de ganancia unitaria mientras mantiene valores constantes para los márgenes de ganancia y fase tiende a aumentar el ancho de banda de bucle cerrado y disminuir el tiempo de subida de bucle cerrado.
Ciertas relaciones entre estas tres cantidades y el rendimiento de bucle cerrado correspondiente se dan en la siguiente sección. Antes de presentar estas relaciones, se enfatiza que la simplicidad y excelencia de los resultados asociados con el análisis de frecuencia-respuesta hacen de este método uno de uso frecuente, particularmente durante la fase inicial de diseño. Una vez determinado un diseño tentativo basado en estos conceptos, se puede investigar información más detallada, como la ubicación exacta de las singularidades de bucle cerrado o la respuesta transitoria del sistema, frecuentemente con la ayuda del cálculo de la máquina.
Rendimiento de bucle cerrado en términos de parámetros de transmisión en bucle
Por lo general, la cantidad se\(a(j\omega )f(j\omega )\) puede obtener de forma rápida y precisa en forma de parcela de bodes. Los efectos de los cambios de parámetros del sistema en la transmisión de bucle también se determinan fácilmente. Por lo tanto, las relaciones aproximadas entre la transmisión en bucle y el rendimiento de bucle cerrado proporcionan una base útil y poderosa para el diseño del sistema de retroalimentación.
La relación entrada-salida para un sistema del tipo ilustrado en la Figura 4.10\(a\) es
\[A(s) = \dfrac{V_o (s)}{V_i (s)} = \dfrac{a(s)}{1 + a(s) f(s)} \nonumber \]
Si el sistema es estable, la función de transferencia de bucle cerrado del sistema puede aproximarse para limitar los valores de transmisión en bucle como
\[A(j \omega ) \simeq \dfrac{1}{f(j \omega )} \ \ \ |a (j \omega ) f (j \omega ) | \gg 1\label{eq4.4.6} \]
\[A(j \omega ) \simeq a(j \omega ) \ \ \ |a (j \omega ) f (j \omega ) | \ll 1 \label{eq4.4.7} \]
Un objetivo en el diseño de los sistemas de retroalimentación es asegurar que la aproximación de la Ecuación\(\ref{eq4.4.6}\) sea válida en todas las frecuencias de interés, de manera que la ganancia de bucle cerrado del sistema sea controlada por el elemento de retroalimentación. La aproximación de la Ecuación\(\ref{eq4.4.7}\) es relativamente poco importante, ya que el sistema es efectivo operando sin retroalimentación en este caso. Si bien normalmente no esperamos que el sistema proporcione ganancia de bucle cerrado controlada con precisión a frecuencias donde la magnitud de la transmisión en bucle sea cercana a una, la discusión de la Sección 4.4.2 muestra que la estabilidad relativa de un sistema está determinada en gran medida por su desempeño en esta frecuencia gama.
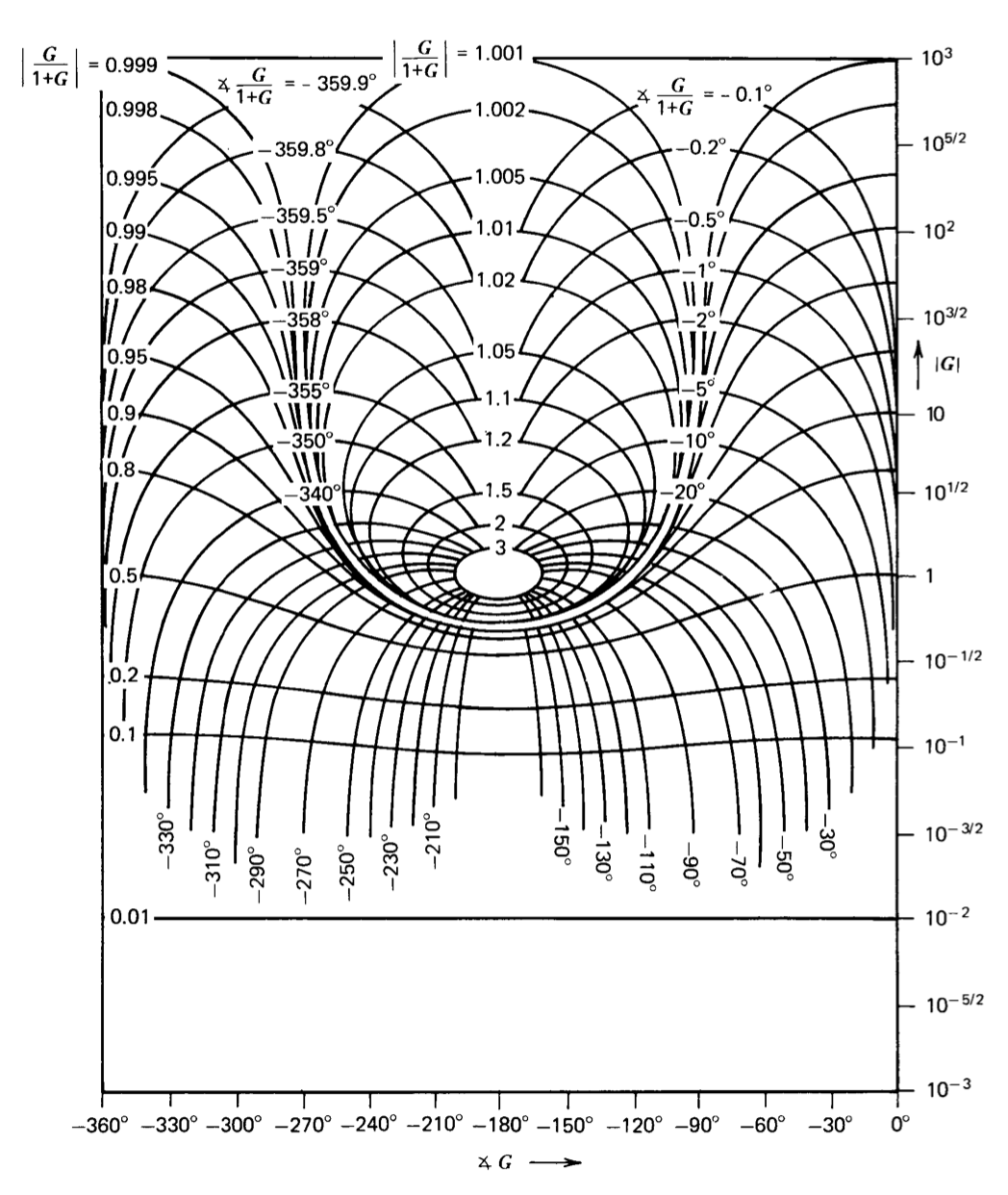
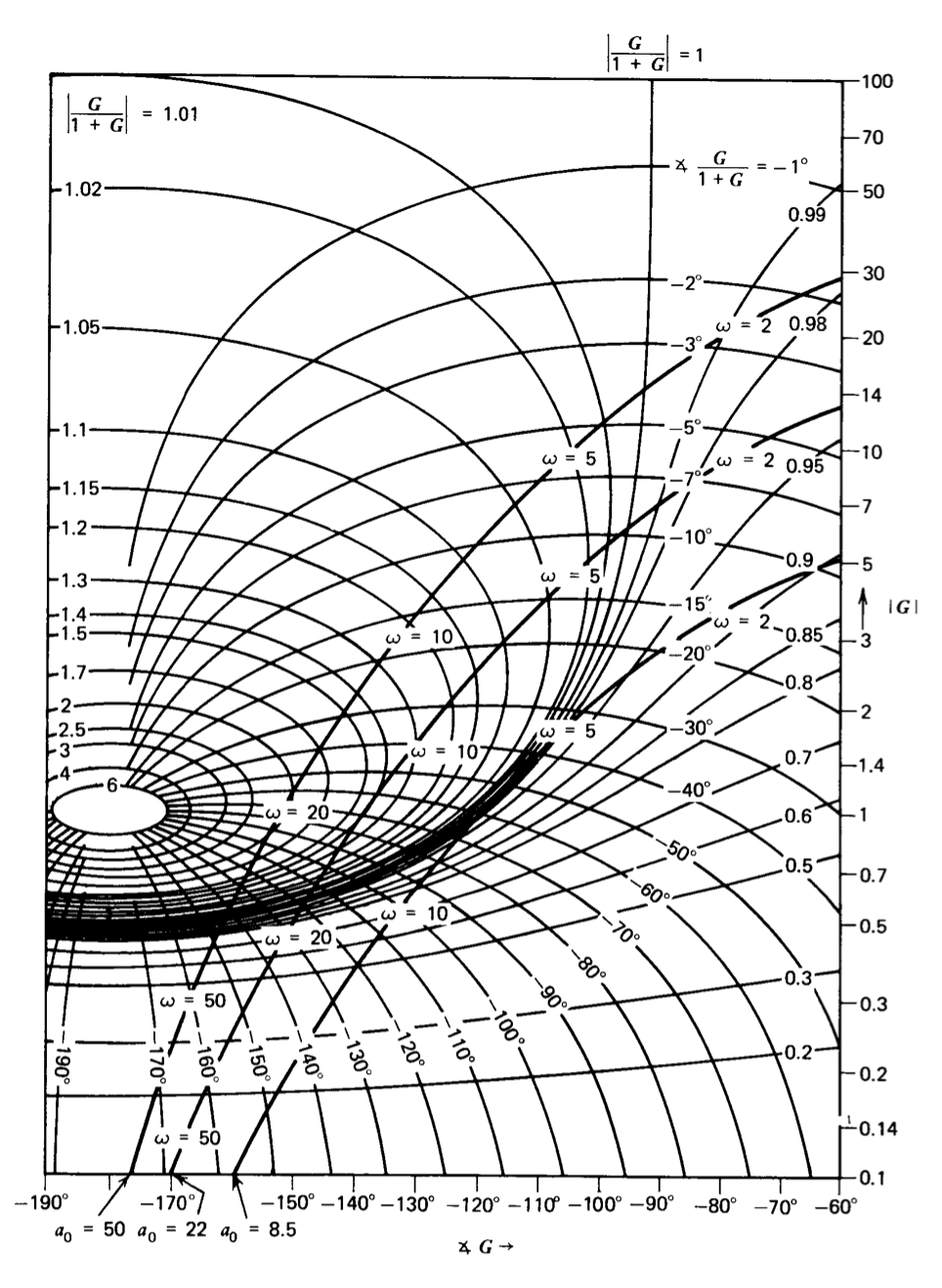
El gráfico Nichols que se muestra en la Figura 4.22 proporciona un método conveniente para evaluar la ganancia de bucle cerrado de un sistema de retroalimentación a partir de su transmisión en bucle, y es particularmente valioso cuando ninguna de las aproximaciones limitantes de la ecuación\(\ref{eq4.4.6}\) y\(\ref{eq4.4.7}\) es válida. Este gráfico se\(G/(1 + G)\) relaciona con\(G\) dónde\(G\) se encuentra cualquier número complejo. Para utilizar el gráfico, el valor de\(G\) se ubica en las coordenadas rectangulares de fase de ganancia. El ángulo y la magnitud de\(G/(1 + G)\) se leen directamente de las coordenadas curvas que se cruzan con el valor de\(G\) seleccionado.
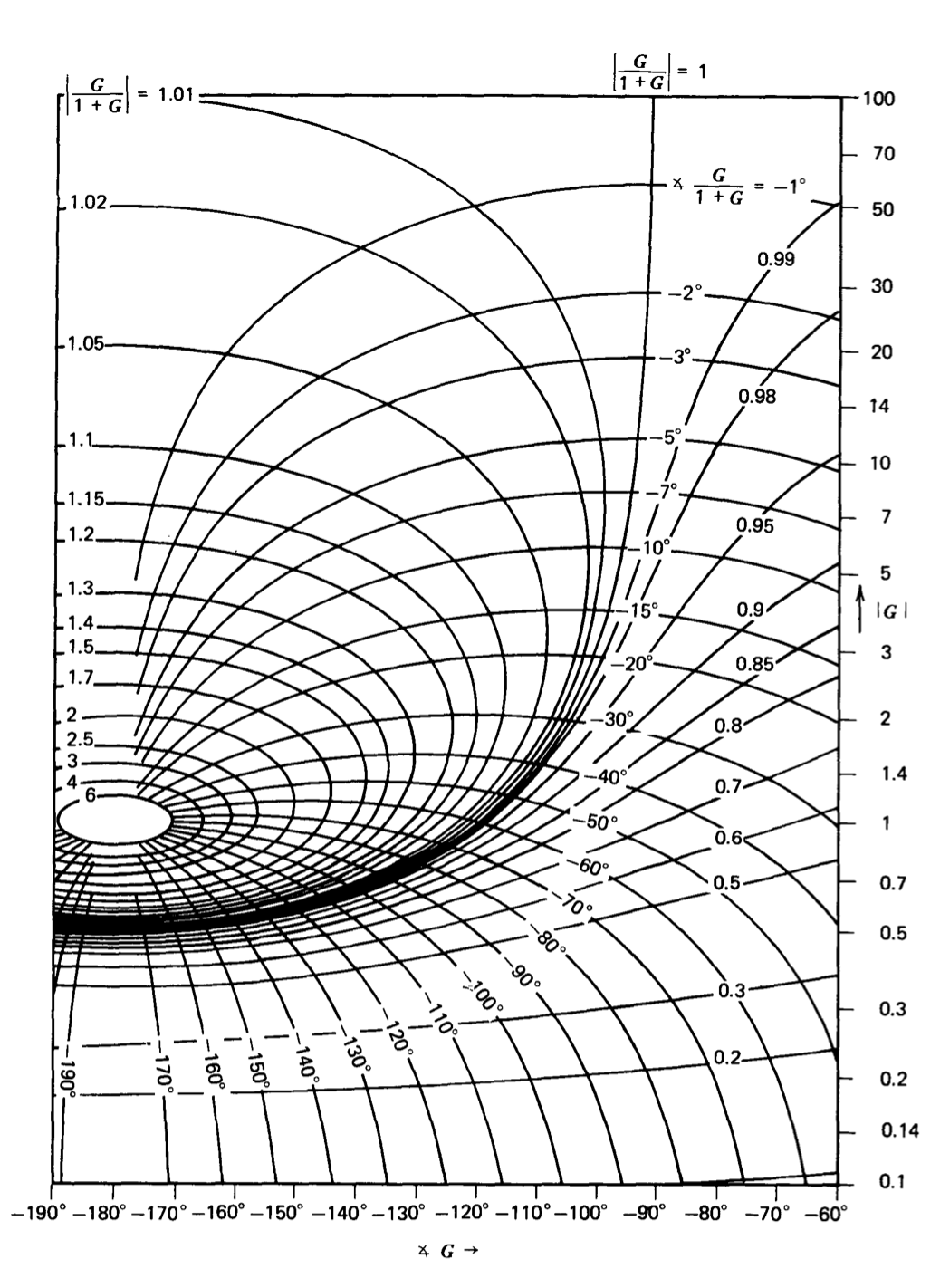
Las coordenadas de fase de ganancia mostradas en la Figura 4.22 cubren el\(-360^{\circ}\) rango completo\(0^{\circ}\) en ángulo y una relación de\(10^6\) magnitud. Este rango de magnitud es innecesario, ya que las aproximaciones de Ecuación\(\ref{eq4.4.6}\) y\(\ref{eq4.4.7}\) suelen ser válidas cuando la magnitud de transmisión en bucle supera 10 o es menor que 0.1. De igual manera, el rango de ángulos de mayor interés es el que rodea el\(-180^{\circ}\) valor y que incluye márgenes de fase anticipados. El gráfico Nichols mostrado en la Figura 4.23 se expande para proporcionar mayor resolución en la región donde normalmente se utilizará.
Una manera efectiva de ver el gráfico Nichols es como una superficie tridimensional, con la altura de la superficie proporcional a la magnitud de la función de transferencia de bucle cerrado correspondiente a los parámetros de transmisión de bucle que definen el punto de interés. Esta visualización muestra una “montaña” (con un pico de altura infinita) donde la transmisión en bucle es +1.
El gráfico Nichols se puede utilizar directamente para cualquier sistema de retroalimentación de ganancia de unidad. La transformación indicada en la Figura 4.10\(b\) muestra que el gráfico puede ser utilizado para sistemas arbitrarios de bucle único observando que
\[A(j \omega) = \dfrac{a(j\omega)}{1 + a(j\omega) f(j \omega)} = \left [\dfrac{a(j\omega) f(j \omega)}{1 + a(j\omega) f(j \omega)} \right ]\left [\dfrac{1}{f(j \omega)} \right ] \nonumber \]
La respuesta de frecuencia de bucle cerrado se determina multiplicando el factor\(a(j\omega) f(j \omega)/[1 + a(j\omega) f(j \omega)]\) obtenido a través del gráfico Nichols\(1/f(j\omega)\) mediante técnicas de Bode.
Una cantidad de interés para los sistemas de retroalimentación con trayectorias de retroalimentación independientes de la frecuencia es la magnitud máxima\(M_p\) igual a la relación de la magnitud máxima de\(A(j\omega)\) su magnitud de baja frecuencia (ver Sección 3.5). Un gran valor para\(M_p\) indica un sistema relativamente menos estable, ya que muestra que hay alguna frecuencia para la cual la ecuación característica se aproxima a cero y así que hay un par de polos de bucle cerrado cerca del eje imaginario a aproximadamente la frecuencia de pico. Los amplificadores de retroalimentación se diseñan frecuentemente para tener\(M_p\) entre 1.1 y 1.5. Los valores más bajos\(M_p\) implican una mayor estabilidad relativa, mientras que los valores más altos indican que la estabilidad se ha visto comprometida para obtener una mayor transmisión en bucle de baja frecuencia y una frecuencia de cruce más alta.
El valor de\(M_p\) para un sistema en particular se puede determinar fácilmente a partir del gráfico Nichols. Además, el gráfico se puede utilizar para evaluar los efectos de las variaciones en la transmisión de bucle en\(M_p\). Una manipulación de uso frecuente determina la relación entre\(M_p\) y\(a_0f_0\) para un sistema con singularidades de transmisión de bucle fijo. La cantidad\(a(j\omega )f(j\omega )/a_0f_0\) se traza primero en coordenadas de fase de ganancia usando la misma escala que el gráfico Nichols. Si esta gráfica se realiza en papel de calco, se puede alinear con la gráfica de Nichols y deslizarse hacia arriba o hacia abajo para ilustrar los efectos de diferentes valores de\(a_0f_0\). La función de transferencia de bucle cerrado se obtiene directamente del gráfico de Nichols evaluando\(A(j\omega )\) a diversas frecuencias, mientras que la curva de mayor magnitud de la gráfica de Nichols tocada\(a(j\omega )f(j\omega )\) por un valor particular de\(a_0f_0\) indica la correspondiente\(M_p\).
La Figura 4.24 muestra esta construcción para un sistema con\(f = 1\) y
\[a(s) = \dfrac{a_0}{(s + 1)(0.1s + 1)} \nonumber \]
Los valores de\(a_0\) para las transmisiones de tres bucles son 8.5, 22 y 50. Los correspondientes\(M_p\) son 1, 1.4 y 2, respectivamente.
Si bien el gráfico Nichols se usa normalmente para determinar la función de bucle cerrado a partir de la transmisión de bucle, es posible usarlo para ir por el otro lado; es decir, para determinar a\(a(j\omega )f(j\omega )\) partir de\(A(j\omega )\). Esta transformación es ocasionalmente útil para el análisis de sistemas para los cuales solo son prácticas las mediciones de bucle cerrado. La transformación produce buenos resultados cuando la magnitud de\(a(j\omega )f(j\omega )\) es cercana a uno. Además, la aproximación de la Ecuación\(\ref{eq4.4.7}\) muestra que\(A(j\omega ) \simeq a(j\omega )\) cuando la magnitud de la transmisión en bucle es pequeña. Sin embargo, la ecuación\(\ref{eq4.4.6}\) indica que\(A(j\omega )\) es esencialmente independiente de la transmisión de bucle cuando la magnitud de la transmisión de bucle es grande. El examen de la gráfica Nichols confirma este resultado ya que muestra que cambios muy pequeños en la magnitud o ángulo de bucle cerrado se traducen en cambios muy grandes en la transmisión de bucle para grandes magnitudes de transmisión de bucle. Por lo tanto, incluso pequeños errores en la medición\(A(j\omega )\) de impiden la estimación de grandes valores para\(a(j\omega )f(j\omega )\) con cualquier precisión.
La estabilidad relativa de un sistema de retroalimentación y muchas otras características importantes de su respuesta de bucle cerrado están determinadas en gran medida por el comportamiento de su transmisión en bucle a frecuencias donde la magnitud de esta cantidad es cercana a la unidad. Las aproximaciones que se presentan a continuación relacionan las cantidades de bucle cerrado definidas en la Sección 3.5 con las propiedades de transmisión en bucle definidas en la Sección 4.4.2. Estas aproximaciones son útiles para predecir la respuesta de bucle cerrado, comparar el rendimiento de varios sistemas y estimar los efectos de los cambios en la transmisión de bucle sobre el rendimiento de bucle cerrado.
Aquí se asumen los supuestos utilizados en la Sección 3.5, en particular que\(f\)\(a_0\) es uno en todas las frecuencias, que es grande, y que la singularidad de frecuencia más baja de\(a(s)\) es un polo. En estas condiciones,
\[M_p \simeq \dfrac{1}{\sin \phi_m}\label{eq4.4.10} \]
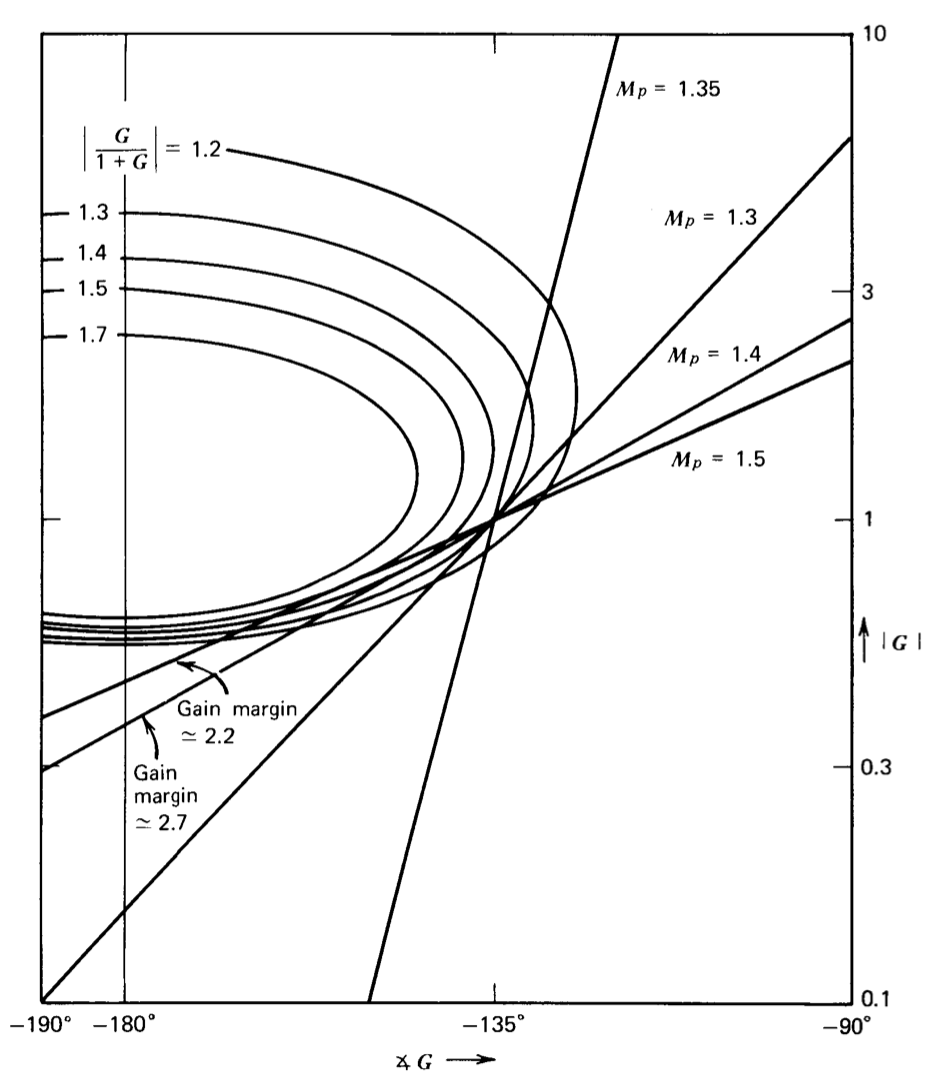
donde\(\phi_m\) está el margen de fase. Las consideraciones que conducen a esta aproximación se ilustran en la Figura 4.25. Esta figura muestra varias curvas de magnitud de bucle cerrado en las proximidades de\(M_p = 1.4\) y supone que el margen de fase del sistema es\(45^{\circ}\). Dado que el punto\(|G| = 1, \measuredangle G = -135^{\circ}\) debe existir para un sistema con un margen de\(45^{\circ}\) fase, no hay manera posible que\(M_p\) pueda ser menor\(M_p\) que aproximadamente 1.3, y la curva de ganancia-fase de transmisión de bucle debe restringirse de manera bastante específica para igualar este valor. Si se asume que la magnitud y el ángulo de\(G\) están linealmente relacionados, las construcciones lineales incluidas en la Figura 4.25 muestran que\(M_p\) no pueden superar aproximadamente 1.5 a menos que el margen de ganancia sea muy pequeño. Los sistemas bien educados son en realidad más propensos a tener una curva de ganancia-fase que proporciona una región extendida de tangencia aproximada a la\(M_p = 1.4\) curva para un margen de fase de\(45^{\circ}\). Se mantienen argumentos similares para otros valores de margen de fase, y la aproximación de Ecuación\(\ref{eq4.4.10}\) representa un buen ajuste a la relación entre el margen de fase y el correspondiente\(M_p\).
Otras dos aproximaciones relacionan la respuesta transitoria del sistema con su frecuencia de cruce\(\omega_c\).
\[\dfrac{0.6}{\omega_c} < t_r < \dfrac{2.2}{\omega_c} \nonumber \]
Los valores más cortos del tiempo de subida corresponden a valores menores del margen de fase.
\[t_s > \dfrac{4}{\omega_c} \nonumber \]
El límite se aproxima únicamente para sistemas con grandes márgenes de fase.
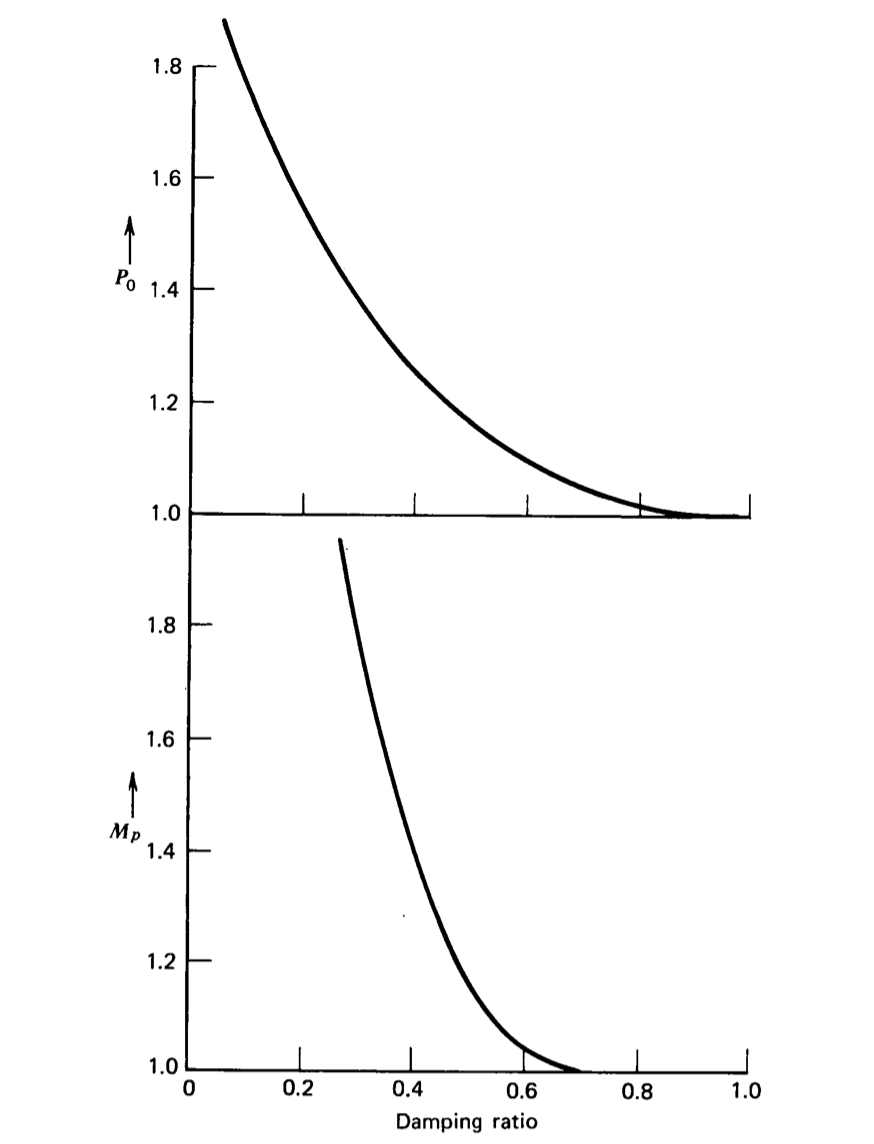
Veremos que la función de transferencia de bucle abierto de muchos amplificadores operativos incluye un polo a bajas frecuencias y un segundo polo cerca de la frecuencia de ganancia unitaria del amplificador. Si la dinámica del sistema está dominada por estos dos polos, la relación de amortiguación y la frecuencia natural de un sistema de segundo orden que se aproxima al sistema de bucle cerrado real se pueden obtener a partir de los parámetros de diagrama de bodes de un sistema con una trayectoria de retroalimentación independiente de la frecuencia utilizando las curvas mostradas en la Figura 4.26 \(a\). Las curvas mostradas en la Figura 4.26\(b\) relacionan sobreimpulso de pico y\(M_p\) para un sistema de segundo orden
a la relación de amortiguación y se derivan usando las Ecuaciones 4.3.24 y 4.3.28. Si bien las relaciones de la Figura 4.26\(a\) son estrictamente válidas solo para un sistema con dos polos ampliamente espaciados en su transmisión de bucle, proporcionan una aproximación precisa siempre que se cumplan dos condiciones.
- La magnitud de la transmisión de bucle del sistema cae como\(1/\omega\) en frecuencias entre una década por debajo del cruce y la siguiente singularidad de frecuencia más alta.
- Otros componentes de la transmisión de bucle proporcionan un desplazamiento de fase negativo adicional en las proximidades de la frecuencia de cruce.
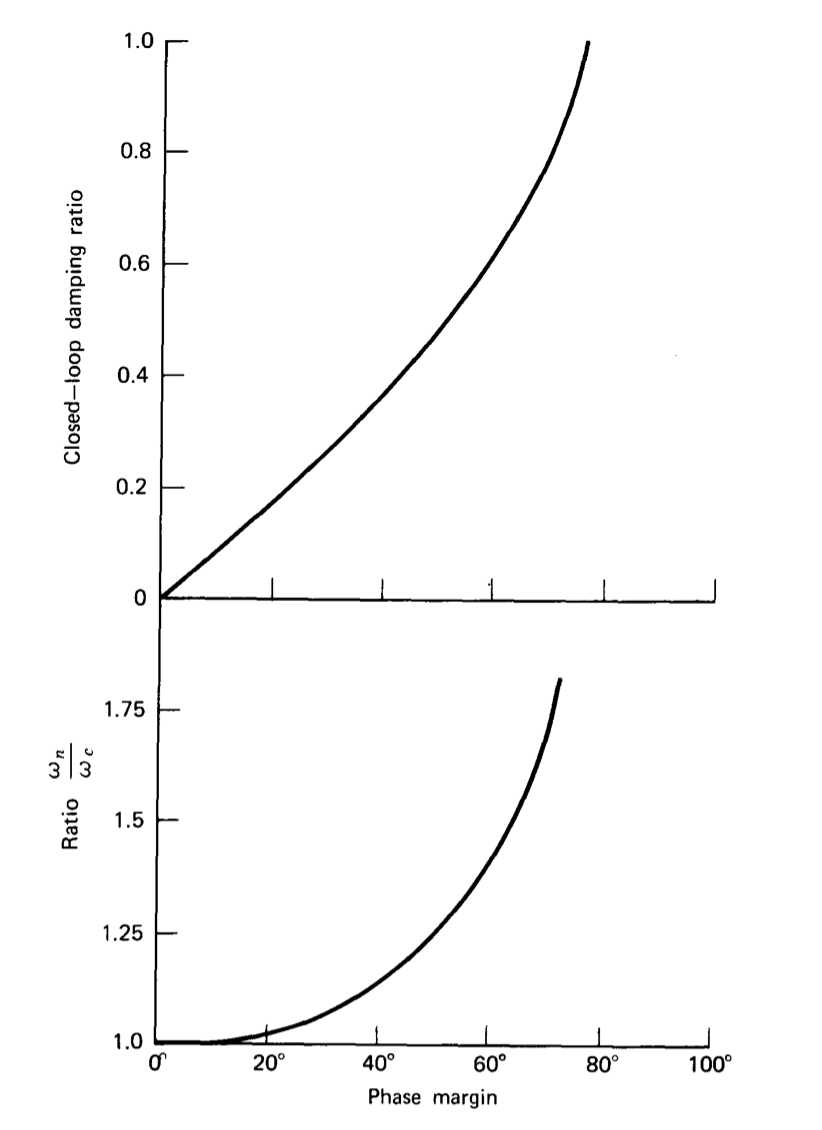
El valor de estas curvas es que proporcionan una manera de determinar un sistema aproximado de segundo orden a partir del margen de fase\(M_p\), o sobreimpulso máximo de un sistema complejo. La validez de este enfoque se debe a que la mayoría de los sistemas deben estar dominados por uno o dos polos en las proximidades de la frecuencia de cruce para obtener un rendimiento aceptable. En secciones posteriores se incluyen ejemplos que ilustran el uso de estas aproximaciones. Veremos que las respuestas transitorias basadas en la aproximación son prácticamente indistinguibles de las del sistema real en muchos casos de interés.
El primer coeficiente de error significativo para un sistema con retroalimentación unitaria también se puede determinar directamente a partir de su diagrama Bode. Si la transmisión en bucle incluye un amplio rango de frecuencias por debajo de la frecuencia de cruce donde su magnitud es igual a\(k/\omega^n\), los coeficientes de error\(e_0\) a través\(e_{n - 1}\) son insignificantes e\(e_n\) iguales\(1/k\).
PROBLEMAS
Ejercicio\(\PageIndex{1}\)
Encuentra el número de ceros de medio plano derecho del polinomio
\[P(s) = s^5 + s^4 + 3s^3 + 4s^2 + s + 2\nonumber \]
Ejercicio\(\PageIndex{2}\)
Un oscilador de cambio de fase se construye con una transmisión de bucle
\[L(s) = -\dfrac{a_0}{(\tau s + 1)^4} \nonumber \]
Utilice la condición Routh para determinar el valor de ao que coloca un par de polos de bucle cerrado en el eje imaginario. Determinar también la ubicación de los postes. Utilice esta información para factorial la ecuación característica del sistema, encontrando así la ubicación de los cuatro polos de bucle cerrado para el valor crítico de\(a_0\).
Ejercicio\(\PageIndex{3}\)
Describir cómo se puede modificar la prueba de Routh para determinar las partes reales de todas las singularidades en un polinomio. También explicar por qué esta modificación suele ser de poco valor como una ayuda computacional para factorizar el polinomio.
Ejercicio\(\PageIndex{4}\)
Demostrar la regla de construcción de locus raíz que establece el ángulo y la intersección de asíntotas de rama con el eje real.
Ejercicio\(\PageIndex{5}\)
Esboce diagramas de locus raíz para el patrón de singularidad de transmisión de bucle mostrado en la Figura 4.27. Evaluar parte\(c\) para valores moderados de\(a_0f_0\), y parte\(d\) para valores moderados y muy grandes de\(a_0f_0\).
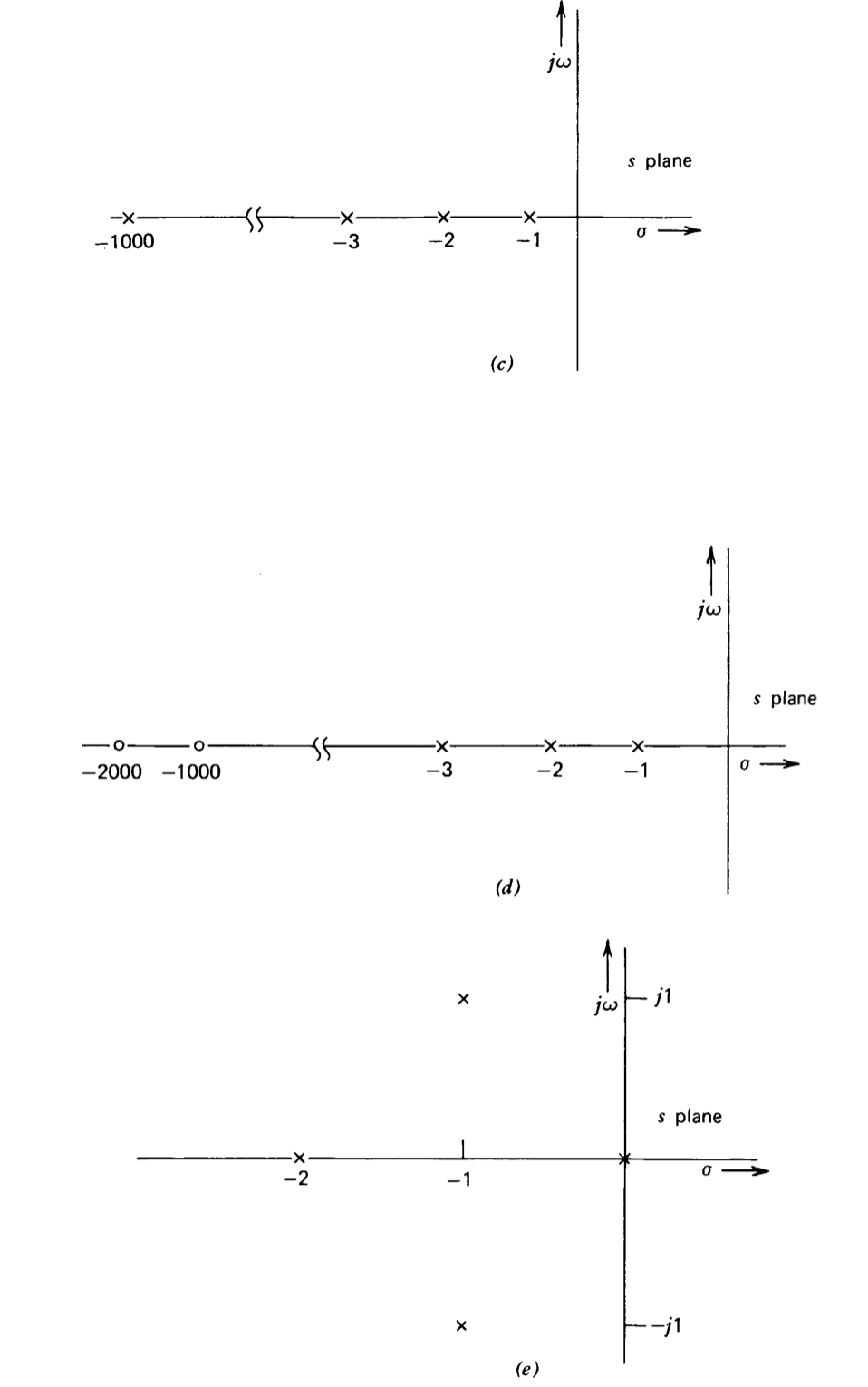
Ejercicio\(\PageIndex{6}\)
Considera dos sistemas, ambos con\(f = 1\). Uno de estos sistemas tiene una función de transferencia de ruta directa
\[a(s) = \dfrac{a_0 (0.5s + 1)}{(s + 1)(0.01s + 1)(0.51 s + 1)} \nonumber \]
mientras que el segundo sistema tiene
\[a'(s) = \dfrac{a_0 (0.51s + 1)}{(s + 1)(0.01s + 1)(0.5 s + 1)} \nonumber \]
El sentido común dicta que las funciones de transferencia de bucle cerrado de estos sistemas deben ser casi idénticas y, además, que ambas deben ser similares a un sistema con
\[a''(s) = \dfrac{a_0}{(s + 1)(0.01s + 1)} \nonumber \]
[Los dobletes polo-cero estrechamente espaciados\(a(s)\) entran y\(a'(s)\) deberían cancelar efectivamente.] Utilice diagramas de locus raíz para mostrar que las respuestas de bucle cerrado son, de hecho, similares.
Ejercicio\(\PageIndex{7}\)
Un amplificador operacional tiene una función de transferencia de bucle abierto
\[a(s) = \dfrac{10^6}{(0.1s + 1)(10^{-6} s + 1)^2}\nonumber \]
Este amplificador se combina con dos resistencias en una configuración de amplificador no inversor. Descuidando la carga, determine el valor de ganancia de bucle cerrado que resulta cuando la relación de amortiguación del par de polos de bucle cerrado complejo es 0.5.
Ejercicio\(\PageIndex{8}\)
Un amplificador operacional tiene una función de transferencia de bucle abierto
\[a(s) = \dfrac{10^5}{(\tau s + 1)(10^{-6} s + 1)}\nonumber \]
La cantidad se\(\tau\) puede ajustar cambiando la compensación del amplificador. Utilice técnicas de contorno de raíz para determinar un valor\(\tau\) que dé como resultado una relación de amortiguación de bucle cerrado de 0.707 cuando el amplificador está conectado como un inversor de ganancia de unidad.
Ejercicio\(\PageIndex{9}\)
Un sistema de retroalimentación que incluye un retardo de tiempo tiene una transmisión en bucle
\[L(s) = -\dfrac{a_0 e^{-0.01 s}}{(s + 1)}\nonumber \]
Utilice la prueba de Nyquist para determinar el valor máximo de\(a_0\) para una operación estable. ¿Qué valor de\(a_0\) debe seleccionarse para limitar\(M_p\) a un factor de 1.4? (Puede suponer que la ruta de retroalimentación del sistema es independiente de la frecuencia).
Ejercicio\(\PageIndex{10}\)
Hemos estado investigando la estabilidad de los sistemas de retroalimentación que generalmente son de naturaleza de paso bajo, ya que las funciones de transferencia de la mayoría de las conexiones operacional-amplificador caen dentro de esta categoría. Sin embargo, también surgen problemas de estabilidad en los sistemas de paso alto. Por ejemplo, los amplificadores de retroalimentación acoplados a-c diseñados para su uso en frecuencias de audio a veces muestran una inestabilidad de baja frecuencia llamada “motor-boating”. Utilice la prueba Nyquist para demostrar la posibilidad de este tipo de inestabilidad para un amplificador con una transmisión en bucle
\[L(s) = -\dfrac{a_0 s^3}{(s + 1)(0.1s + 1)^2}\nonumber \]
También muestran el comportamiento potencialmente inestable usando métodos de locus raíz. ¿Para qué rango de valores\(a_0\) es estable el amplificador?
Ejercicio\(\PageIndex{11}\)
Desarrolle una modificación de la prueba Nyquist que le permita determinar si un sistema de retroalimentación tiene polos de bucle cerrado con una relación de amortiguación inferior a 0.707. Ilustre su prueba formando el diagrama Nyquist modificado para un sistema con\(a(s) = a_0/(s + 1)^2\),\(f(s) = 1\). ¿Para qué valor de\(a_0\) la relación de amortiguación del par de polos de bucle cerrado es igual a 0.707? Verifica tu respuesta factorizando la ecuación característica para este valor de\(a_0\).
Ejercicio\(\PageIndex{12}\)
La función de transferencia de bucle abierto de un amplificador operacional es
\[a(s) = \dfrac{10^5}{(0.1s + 1)(10^{-6} s + 1)^2}\nonumber \]
Determine el margen de ganancia, el margen de fase, la frecuencia de cruce, y\(M_p\) para este amplificador cuando se usa en una conexión de retroalimentación con\(f = 1\). También encuentra el valor de descuento que resulta en un\(M_p\) de 1.1. ¿Para qué sirven los valores de margen de fase y ganancia y frecuencia de cruce con este valor\(f\)?
Ejercicio\(\PageIndex{13}\)
Un sistema de retroalimentación se construye con
\[a(s) = \dfrac{10^6 (0.01s + 1)^2}{(s+1)^3}\nonumber \]
y un valor ajustable e independiente de la frecuencia para\(f\). A medida que\(f\) se incrementa de cero, se observa que el sistema es estable para valores muy pequeños apagados, luego se vuelve inestable, y eventualmente vuelve a un comportamiento estable para valores suficientemente altos de\(f\). Explicar este desempeño usando Nyquist y análisis de locus raíz. Utilice el criterio Routh para determinar los dos valores límite para\(f\).
Ejercicio\(\PageIndex{14}\)
Un amplificador operacional con una trayectoria de retroalimentación independiente de la frecuencia exhibe 40% de sobreimpulso y de 10 a 90% de tiempo de subida de 0.5 ps en respuesta a una entrada de paso. Estimar el margen de fase y la frecuencia de cruce de la conexión de retroalimentación, asumiendo que su rendimiento está dominado por dos polos de transmisión de bucle ampliamente separados.
Ejercicio\(\PageIndex{15}\)
Considere un sistema de retroalimentación con
\[a(s) = \dfrac{a_0}{s[(s^2/2) + s +1]}\nonumber \]
y\(f(s) = 1\).
Demostrar que mediante la elección apropiada de ao, los polos de bucle cerrado del sistema se pueden colocar en un patrón Butterworth de tercer orden. Encuentre la frecuencia de cruce y el margen de fase de la transmisión de bucle cuando\(a_0\) se seleccione para la respuesta de Butterworth de bucle cerrado. Utilice estas cantidades junto con la Figura 4.26 para encontrar la relación de amortiguación y la frecuencia natural de un sistema de segundo orden que se puede utilizar para aproximar la respuesta transitoria del filtro Butterworth de tercer orden. Comparar el sobreimpulso máximo y el tiempo de subida del sistema de aproximación en respuesta a un paso con los de la respuesta de Butterworth (Figura 3.10). Obsérvese que, aunque este sistema es considerablemente diferente al utilizado para desarrollar la Figura 4.26, la aproximación predice parámetros en el dominio del tiempo con una precisión justa.


