9.2: ANÁLISIS

Para demostrar las características de rendimiento del amplificador introducido en la sección anterior, es necesario aproximar analíticamente algunas de sus características más importantes. Si bien los detalles exactos del análisis son específicos de este amplificador, varias características significativas, particularmente las relacionadas con la dinámica y la compensación, son comunes a todos los amplificadores operativos de dos etapas. Así, las conclusiones a las que llegaremos se extienden más allá de este circuito particular.

Debemos darnos cuenta de que ciertos aspectos del siguiente análisis probablemente estén en error por un factor de dos o más, ya que la incertidumbre de algunos de los valores de los parámetros asociados a los transistores limita la precisión. Otro tipo de dificultad se encuentra en el análisis de la dinámica del amplificador, ya que se pronostican una serie de polos en las proximidades del\(f_T\) de los transistores utilizados en el amplificador. Dichos resultados siempre son sospechosos porque las deficiencias del modelo de transistor impiden un análisis preciso en este rango de frecuencias. Afortunadamente, estas imprecisiones son de poca preocupación ya que nuestro objetivo no es tanto la predicción precisa del rendimiento de este amplificador en particular, ya que es una comprensión de las características importantes de este tipo general de amplificador.

Ganancia de baja frecuencia

Una característica importante de un amplificador operacional es su ganancia de bucle abierto d-c. El cálculo de la ganancia de este amplificador es necesario porque la medición precisa de los niveles de señal que permitiría la determinación experimental de ganancia está excluida por el ruido y la deriva.

Con mucho, la mayor fracción de la ganancia de baja frecuencia del amplificador ocurre en la etapa de cascode para esta implementación particular de la topología básica. El análisis del amplificador completo se facilita desarrollando inicialmente un circuito equivalente de baja frecuencia para el amplificador cascode. El análisis de la Sección 8.3.4 mostró que la ganancia de voltaje de un amplificador cascode descargado es

\[-\dfrac{\beta_6}{2 \eta_6} = -\dfrac{g_{m6} r_{\mu 6}}{2}\nonumber \]

Figura 9.2 Circuito equivalente para amplificador cascode a bajas frecuencias.

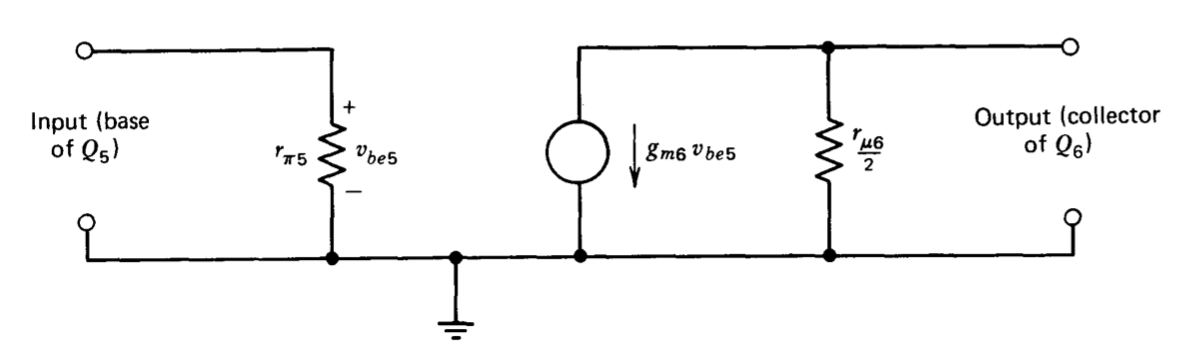
mientras que su resistencia de entrada es\(r_{\pi 5}\). (Los subíndices que diferencian entre los dos transistores en la conexión cascode se refieren a la Figura 9.1.) Si bien la resistencia de salida de la conexión cascode no se calculó específicamente, se puede usar un resultado de la Sección 8.3.5 para determinar esta cantidad. La ecuación 8.3.47 da\(r_{\mu} /2\) como la resistencia de salida de una fuente de corriente de base común con una gran resistencia incremental del emisor-circuito. La resistencia de salida del cascode debe ser idéntica ya que su salida consiste en una conexión de base común con una gran resistencia emisor-circuito. Estos resultados muestran que el rendimiento de baja frecuencia de la porción de cascode del amplificador puede ser modelado por el circuito equivalente de la Figura 9.2.

La ganancia d-c del circuito mostrado en la Figura 9.1 se determina utilizando los valores de los parámetros mostrados en la Tabla 9.1 para los transistores. El cálculo se realiza asumiendo que la entrada no inversora del amplificador está puesta a tierra de manera incremental. Esta suposición arroja el mismo valor para la ganancia d-c que se obtendría considerando un voltaje de entrada diferencial verdadero. Poner a tierra incrementalmente la entrada no inversora elimina un término insignificante de alta frecuencia en la función de transferencia que resulta de las señales alimentadas a través de la capacitancia colector-base de\(Q_2\) (ver Sección 8.2.3).

Tabla 9.1 Parámetros del transistor para el circuito de la figura 9.1

Número de transistor	Tipo	\(I_C\) o \(I_D\) (\(\mu A\))	\(g_m\) (mmho)	\(\beta\)	\(r_{\pi}\) (\(k\Omega\))	\(r_{\mu}\) (\(k\Omega\))	\(r_{o}\) (\(k\Omega\))	\(C_{\mu}\) o \(C_{gd}\) (pF)	\(C_{\pi}\) o \(C_{gs}\) (pF)
\(Q_1, Q_2\)	2N5963	10	0.4	1100	2750	*	*	6	10
\(Q_3\)	2N3707	20	*	*	*	*	*	8	10
\(Q_4, Q_5, Q_6\)	2N4250	50	2	350	175	500	1.4	10	15
\(Q_7\)	2N3707	50	2	200	100	500	2.5	8	10
\(Q_8\)	TIS58	2 mA	*	-	-	-	-	2	*
\(Q_9\)	2N3707	2 mA	*	*	*	*	*	*	*
\(Q_{10}\)	2N2219	*	*	200	*	*	*	*	*
\(Q_{11}\)	2N2905	*	*	200	*	*	*	*	*
\(Q_{12}\)	2N3707	0	*	*	*	*	*	*	*
\(Q_{13}\)	2N4250	0	*	*	*	*	*	*	*

- No relevante.
* Valor sin importancia en el análisis incluido.

La ganancia general se encuentra calculando primero las relaciones de transferencia para varias partes del circuito. Un voltaje de entrada incremental aplicado a la base de\(Q_1\),\(v_i\), provoca un cambio en la corriente del colector de\(Q_2\) dado por

\[i_{c2} = -\dfrac{v_i g_{m1}}{2}\label{eq9.2.1} \]

(Se ha supuesto que ambos transistores de entrada están operando a corrientes iguales de manera que\(g_{m1} = g_{m2}\).)

El circuito equivalente cascode desarrollado previamente muestra que el cambio en la tensión base de\(Q_5\) está relacionado con el cambio de\(Q_2\) corriente colector-por

\[v_{be5} = -i_{c2} (325 k\Omega || r_{\pi 5})\label{eq9.2.2} \]

(Se ha supuesto que el potenciómetro del circuito colector está configurado en la posición central para que la resistencia de carga del transistor\(Q_2\) sea igual a\(325\ k\Omega\).) Para determinar la ganancia de voltaje del amplificador cascode, es necesario calcular la carga aplicada al mismo. La resistencia de entrada del transistor de efecto de campo\(Q_8\) es esencialmente infinita, mientras que la resistencia de salida para la fuente de corriente\(Q_7\) es

\[r_{\mu 7} \left | \right | \left [\dfrac{1 + g_{m7} (r_{\pi 7} || 68 k \Omega)}{g_{o7}} \right ] \nonumber \]

(Ver Ecuación 8.3.45.) Es computacionalmente conveniente reducir esta ecuación ahora e introducir la suposición experimentalmente verificable de que\(r_{\mu 7} \simeq r_{\mu 6}\). Este valor es razonable, ya que ambos dispositivos funcionan a corrientes idénticas, y se fabrican utilizando procesos similares (aunque complementarios). El 2N3707 tiene un típico\(\beta\) de 200 at\(50\ \mu A\), por lo que\(r_{\pi 7}\) es típicamente\(100\ k\Omega\) en esta corriente. Por lo tanto,\(r_{\pi 7} || 68 k\Omega \simeq 0.4r_{\pi 7}\). En consecuencia, la resistencia de salida de\(Q_7\) se convierte

\[r_{\mu 7} \left | \right | \left [\dfrac{1 + g_{m7} (0.4 r_{\pi 7})}{g_{o7}} \simeq r_{\mu 7} \left | \right | \left [ \dfrac{0.4 \beta_7}{g_{o7}} \right ] = r_{\mu 7} || 0.4 r_{\mu 7} \simeq 0.28 r_{\mu 7} \right ]\label{eq9.2.4} \]

Usando esta relación, la equivalencia asumida de\(r_{\mu 7}\) y\(r_{\mu 6}\), y el modelo de la Figura 9.2 muestra que la ganancia de voltaje cascode cargada es

\[\dfrac{v_{cb6}}{v_{be5}} \simeq -g_{m6} \left (\dfrac{r_{\mu 6}}{2} || 0.28 r_{\mu 6} \right ) \simeq -g_{m6} (0.18 r_{\mu 6} )\label{eq9.2.5} \]

Reconociendo que la ganancia de voltaje descargada desde el colector\(Q_6\) hasta la salida del amplificador es unidad y combina ecuaciones\(\ref{eq9.2.1}\),\(\ref{eq9.2.2}\), y\(\ref{eq9.2.5}\) rendimientos

\[\dfrac{v_o}{v_i} = -\dfrac{g_{m1}}{2} (325 k\Omega || r_{\pi 5}) g_{m6} (0.18 r_{\mu 6}) \label{eq9.2.6} \]

Sustituir los valores de los parámetros de la Tabla 9.1 a la Ecuación\(\ref{eq9.2.6}\) predice una magnitud de ganancia de bucle abierto d-c de\(4 \times 10^6\). La ganancia está dominada por la contribución\(1.8 \times 10^5\) del amplificador cascode (ver Ecuación\(\ref{eq9.2.5}\)).

Función de transferencia

Las ubicaciones de todos los polos y ceros del amplificador podrían predecirse para el circuito completo sustituyendo los modelos incrementales apropiados por los dispositivos activos, aunque esto sería una tarea formidable incluso con la ayuda de una computadora. El enfoque utilizado aquí es hacer aproximaciones relativamente crudas para obtener información sobre la dinámica de control del amplificador y luego verificar los resultados aproximados con un análisis por computadora más detallado (aunque aún incompleto).

La ganancia de voltaje de baja frecuencia descargada del amplificador de búfer (transistores\(Q_8\) a través\(Q_{11}\)) es la unidad. Las cargas del amplificador tan bajas como varios cientos de ohmios no alteran apreciablemente su rendimiento. Si la carga aplicada al amplificador no es capacitiva, la respuesta de frecuencia del búfer se acerca a la\(f_T\) de los dispositivos utilizados en él. Además, la impedancia de entrada de\(Q_8\), que carga el amplificador cascode, es independiente de cualquier carga aplicada a la salida del amplificador ya que el FET es unilateral. Así, la influencia del búfer se puede modelar simplemente usando la capacitancia de entrada de\(Q_8, C_{gd8}\), como carga para el cascode. De igual manera, la carga del transistor\(Q_7\) puede representarse como una impedancia paralela que consiste en su capacitancia de salida\(C_{\mu 7}\) y resistencia de salida 0.28\(r_{\mu 7}\) (Ecuación\(\ref{eq9.2.4}\)).

Figura 9.3 Modelo utilizado para determinar la función de transferencia.

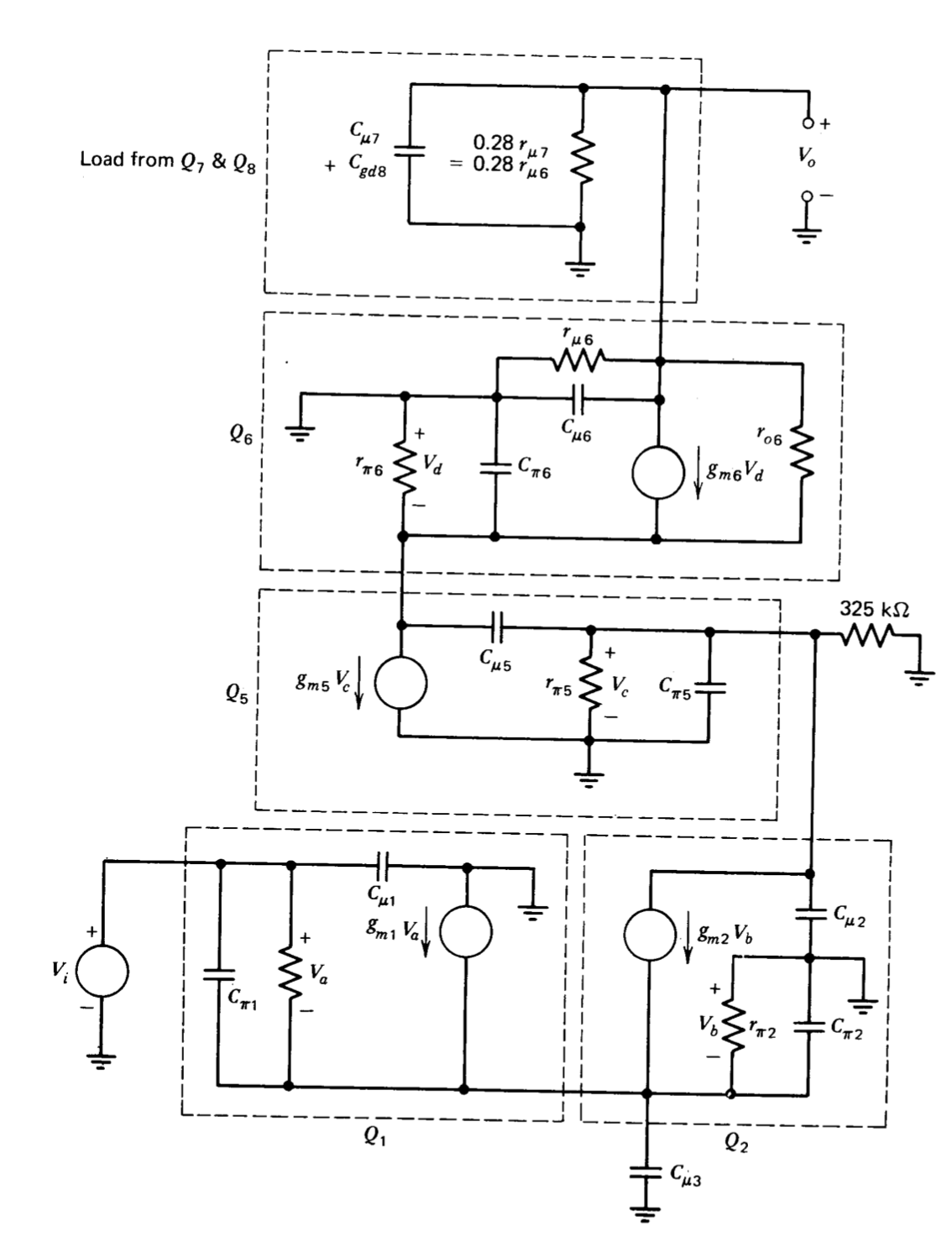
En la Figura 9.3 se muestra un modelo incremental que refleja estas simplificaciones. También se han ignorado las resistencias de base de todos los transistores, así como\(r_{\mu}\)\(r_o\) de los transistores que no sean\(Q_6\) y\(Q_7\) (los transistores en la parte de alta ganancia del circuito).\(r_x\) Para simplificar aún más este modelo se utiliza un argumento basado en el concepto de constantes de tiempo en circuito abierto (Véase P. E. Gray y C. L. Searle, Electronic Principles: Physics, Models, and Circuits, Wiley, Nueva York, 1969, Capítulos 15 y 16.). Las resistencias de circuito abierto (La resistencia de circuito abierto frente a un condensador es la resistencia incremental en el par de terminales en cuestión calculada con todos los demás condensadores en el circuito eliminado o en circuito abierto.) condensadores enfrentados\(C_{\pi 1}\)\(C_{\mu 1}\),\(C_{\pi 2}\),\(C_{\mu 3}\), y\(C_{\pi 6}\) son todo en el orden de\(1/g_m\), para el transistor relacionado o inferior. Por lo tanto, estos condensadores no afectan la dinámica del amplificador a frecuencias bajas en comparación con las\(f_T\)'s de los diversos transistores y se eliminan para la aproximación inicial. Como resultado de esta aproximación, la única contribución de la etapa de entrada a la dinámica del amplificador es una consecuencia de la carga que\(C_{\mu 2}\) se aplica a la base de\(Q_5\), y la etapa misma puede modelarse como una sola fuente de corriente dependiente.

Figura 9.4 Simplificación de la Figura 9.3.

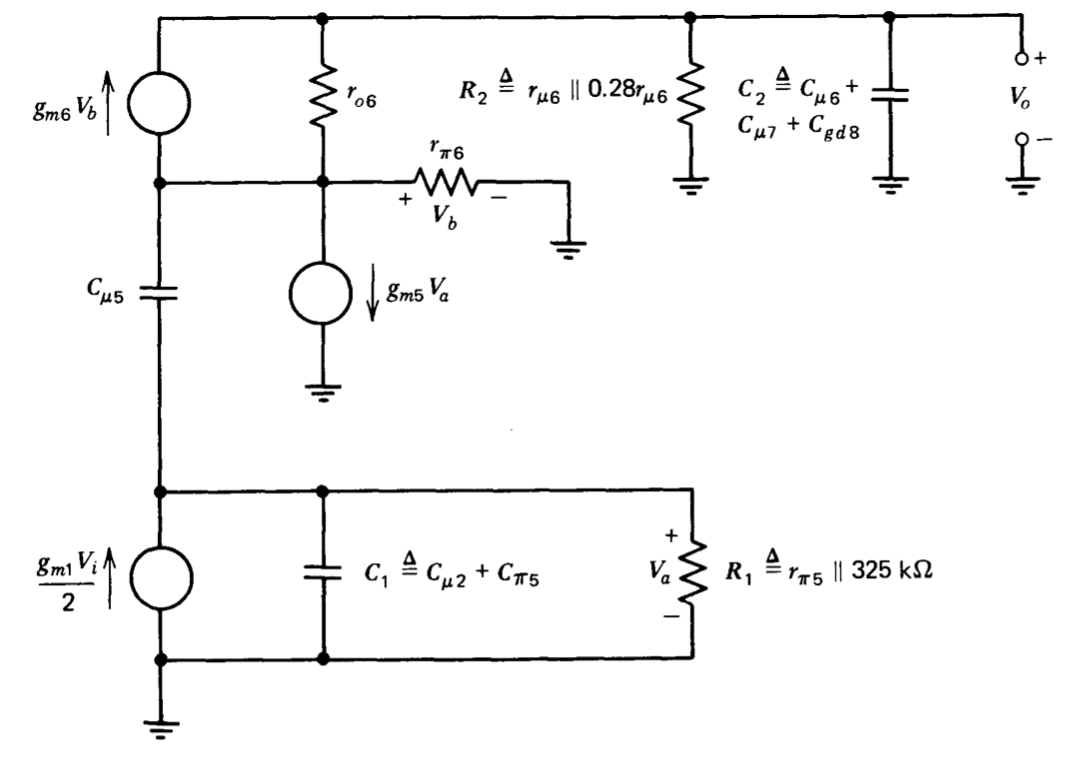
El modelo incremental más simplificado que incorpora las aproximaciones introducidas anteriormente y que se muestra en la Figura 9.4 se utiliza para aproximar la ubicación de los dos polos amplificadores de baja frecuencia. Las ecuaciones de nodo para este circuito son

\[\begin{array} {rcl} {\dfrac{g_{m1} V_i}{2}} & = & {[(C_1 + C_{\mu 5}) s + G_1] V_a - C_{\mu 5} s V_b} \\ {0} & = & {(-C_{\mu 5} s + g_{m5})V_a + (C_{\mu 5} s + g_{m6} + g_{\pi 6} + g_{o 6}) V_b - g_{o6} V_o} \\ {0} & = & {(-g_{m6} - g_{o6})V_b + (C_2 s + g_{o6} + G_2)V_o} \end{array}\label{eq9.2.7} \]

(Ver Figura 9.4 para la definición de parámetros en esta ecuación.)

Los polos se encuentran equiparando el determinante de la matriz de coeficientes de Ecuación\(\ref{eq9.2.7}\) a cero, rindiendo

\[\dfrac{C_1C_2C_{\mu 5}}{g_{m6} G_1 (G_2 + g_{\mu 6})} s^3 + \dfrac{C_2(C_1 + 2C_{\mu 5}}{G_1 (G_2 + g_{\mu 6})} s^2 + \dfrac{C_2}{C_2 + g_{\mu 6}} s + 1 = 0\label{eq9.2.8} \]

Al reducir Ecuación\(\ref{eq9.2.7}\) a\(\ref{eq9.2.8}\), se han caído términos pequeños. Sin embargo, sólo se han eliminado términos que son pequeños debido a desigualdades de transistores y topológicas como\(g_m \gg g_{\pi} \gg g_o \gg g_{\mu}\), y\(C_2 > C_{\mu 6}\) ya\(C_{\mu 6}\) que un componente de\(C_2\) es. Así, las conclusiones que se extraerán de la Ecuación\(\ref{eq9.2.8}\) son aplicables a una variedad de circuitos que comparten esta topología en lugar de limitarse a la elección específica de los valores de los elementos mostrados en la Figura 9.1. Las relaciones fundamentales entre los valores de los parámetros también aseguran que los tres polos representados por\(\ref{eq9.2.8}\) serán reales y ampliamente espaciados. En consecuencia, esta ecuación cúbica se puede factorizar fácilmente, ya que

\[(\tau_a s + 1)(\tau_b s + 1) (\tau_c s + 1) \simeq \tau_a \tau_b \tau_c s^3 + \tau_a \tau_b s^2 + \tau_a s + 1 \text{ for } \tau_a \gg \tau_b \gg \tau_c \label{eq9.2.9} \]

La ecuación nos\(\ref{eq9.2.9}\) permite escribir la ecuación\(\ref{eq9.2.8}\) como

\[\left (\dfrac{C_2}{C_2 + g_{\mu 6}} s + 1 \right ) \left (\dfrac{C_1 + 2C_{\mu 5}}{G_1} s + 1 \right ) \left (\dfrac{C_1C_{\mu 5}}{g_{m6} (C_1 + 2C_{\mu 5})} s + 1 \right ) = 0 \nonumber \]

indicando que

\[\begin{array} {rcl} {\tau_a} & = & {\dfrac{C_2}{G_2 + g_{\mu 6}}} \\ {\tau_b} & = & {\dfrac{C_1 + 2C_{\mu 5}}{G_1}} \\ {\tau_c} & = & {\dfrac{C_1 C_{\mu 5}}{g_{m6} (C_1 + 2C_{\mu 5})}} \end{array} \label{eq9.2.11} \]

La interpretación física de las constantes de tiempo permite conocer el funcionamiento del circuito. La resistencia asociada con la constante de tiempo\(\tau_a\) es simplemente la resistencia incremental desde el nodo de alta resistencia (el colector de\(Q_6\)) a tierra. [Recordemos que\(1/(G_2 + g_{\mu 6}) =0.28r_{\mu 6} || r_{\mu 6} || r_{\mu 6} = 0.18r_{\mu 6}\), el valor obtenido anteriormente y utilizado en la Ecuación\(\ref{eq9.2.5}\) para la resistencia incremental de este nodo a tierra.] De manera similar, la capacitancia\(C_2 = C_{\mu 6} + C_{\mu 7} + C_{gd8}\) es la capacitancia desde el nodo de alta resistencia a tierra. Dado que la capacitancia de todos los nodos amplificadores es del mismo orden de magnitud, no es sorprendente que el polo amplificador dominante esté asociado con el almacenamiento de energía en el nodo de mayor resistencia. Sustituir valores de la Tabla 9.1 muestra que\(\tau_a = 1.8\ ms\), lo que implica que el polo de bucle abierto del amplificador dominante se encuentra en\(s = - 550\text{ sec}^{-1}\).

La constante de tiempo\(\tau_b\) se asocia con la resistencia y capacitancia desde la base\(Q_5\) a tierra. La conductancia\(G_1\) en Ecuación se\(\ref{eq9.2.11}\) definió previamente como la conductancia de este nodo a tierra. La capacitancia consiste en la capacitancia colector a base de\(Q_2\) que deriva este nodo y la capacitancia de entrada efectiva total (incluida la atribuida al efecto Miller) se\(Q_5\) visualizaría si este transistor se cargara con una carga resistiva igual a\(1/g_{m5}\). Tenga en cuenta que a frecuencias muy superiores a\(1/\tau_a\) radianes por segundo, la carga capacitiva en el colector de\(Q_6\) ha reducido la ganancia de voltaje de este transistor; como resultado, no hay retroalimentación significativa al emisor de\(Q_6\) through\(r_{o6}\) a estas frecuencias. Así transistor\(Q_6\) proporciona la\(1/g_{m6} = 1/g_{m5}\) carga para\(Q_5\). La constante de tiempo rb es igual a\(4.5\ \mu s\), lo que implica que el segundo polo amplificador se encuentra en\(s = -2.2 \times 10^5 \text{ sec}^{-1}\). La constante de tiempo\(\tau_c\) corresponde a una frecuencia que se aproxima\(f_T\) para los transistores en el circuito, y así a uno de los muchos polos de alta frecuencia que se ignoran en el análisis simplificado.

Combinando la ganancia d-c (Ecuación\(\ref{eq9.2.6}\)) con la dinámica predicha por encima de los rendimientos

\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{-4 \times 10^6}{(1.8 \times 10^{-3} s + 1)(4.5 \times 10^{-6} s + 1)}\label{eq9.2.12} \]

Figura 9.5 Función de transferencia de bucle abierto del amplificador basada en dos polos de frecuencia más baja (sin compensación).

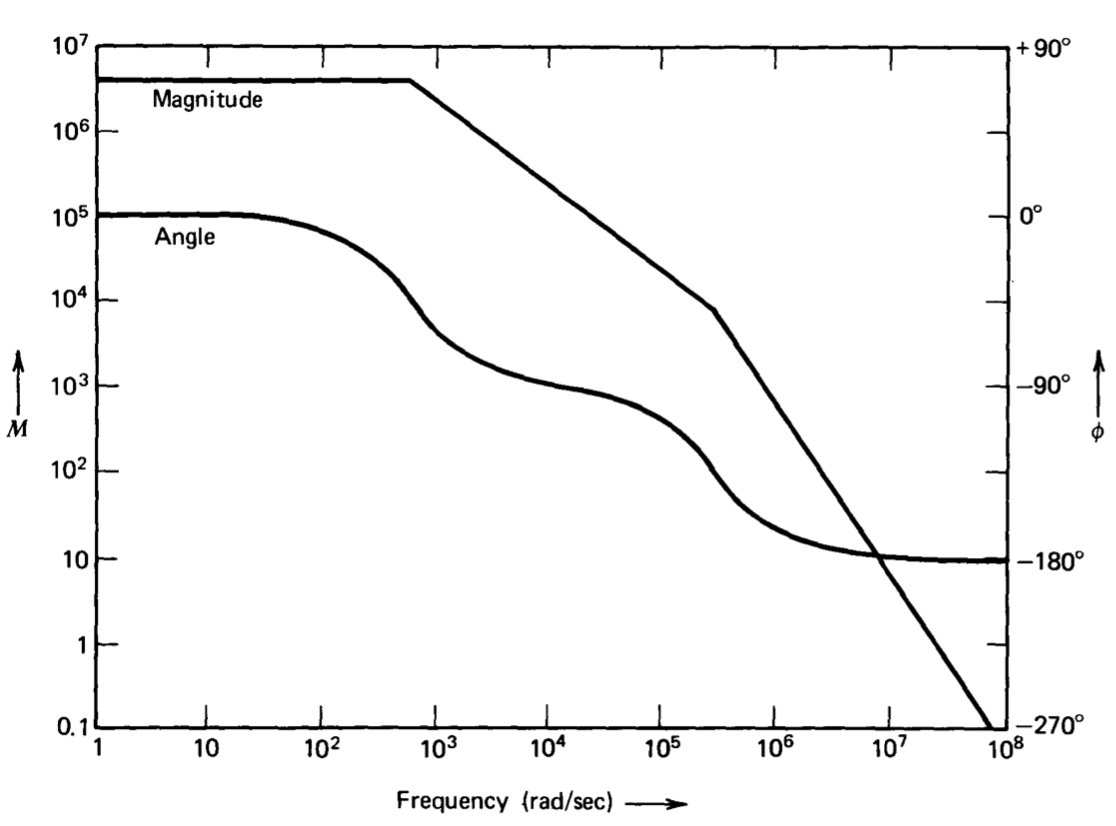
\(\ref{eq9.2.12}\)La ecuación se muestra como una gráfica de Bode (La función de transferencia trazada en la Figura 9.5 es en realidad el negativo de la Ecuación\(\ref{eq9.2.12}\). Esta modificación se realiza porque anticipamos usar el amplificador en conexiones de retroalimentación negativa. Dado que la transmisión en bucle tiene el mismo signo que la ganancia calculada para el amplificador en estas aplicaciones, trazar el negativo de la ganancia del amplificador sigue la convención de trazar el negativo de la transmisión en bucle de un sistema de retroalimentación. Visto alternativamente, la función de transferencia trazada en la Figura 9.5 resultaría si la señal de entrada se aplicara al terminal de entrada no inversora del amplificador.) en la Figura 9.5.

Las ubicaciones de los polos para este diseño también fueron pronosticadas por análisis por computadora, con el fin de verificar algunos de los supuestos introducidos en el desarrollo anterior. Se analizó el circuito equivalente de la Figura 9.3 con resistencias de\(100-\Omega\) base añadidas al modelo de circuito para cada transistor. De esta manera solo se eliminó el amplificador buffer de los cálculos de la computadora. Las locaciones de los dos polos dominantes predichas por la computadora fueron\(- 520\text{ sec}^{-1}\) y\(- 2.15 \times 10^5\text{ sec}^{-1}\). Todos los demás polos tenían frecuencias de ruptura superiores a\(10^7\) radianes por segundo. A pesar de las aproximaciones aparentemente drásticas incluidas en el análisis de este circuito, las ubicaciones predichas de los dos polos dominantes son confirmadas por el cálculo por computadora a errores de redondeo dentro.

Método de Compensación

La función de transferencia de este amplificador (Ecuación\(\ref{eq9.2.12}\)) tiene los polos separados por un factor de 400, y en muchos amplificadores de retroalimentación esta cantidad de separación parecería ideal desde el punto de vista de la estabilidad. Desafortunadamente, con la ganancia masiva de bucle abierto de baja frecuencia característica de los amplificadores operativos (\(4 \times 10^6\)en este diseño), se requiere una mayor separación para asegurar la estabilidad adecuada en muchas aplicaciones. Por ejemplo, si el amplificador se utiliza como seguidor de unidad-ganancia conectando su salida a su entrada inversora, se forma un bucle con\(a(j\omega )\) como se muestra en la Figura 9.5 y\(f = 1\). La gráfica Bode muestra que el margen de fase del sistema es aproximadamente\(0.5^{\circ}\) en este caso, claramente un valor insatisfactorio. En la práctica, esta configuración sería inestable, ya que el desplazamiento de fase negativo asociado con singularidades descuidadas de bucle abierto es mucho mayor que\(0.5^{\circ}\) en la frecuencia de unidad-ganancia del amplificador. Es claro que se debe usar algún método para modificar la función de transferencia de bucle abierto del amplificador con el fin de lograr un rendimiento aceptable en esta y muchas otras conexiones.

Una de las ventajas significativas de la configuración del amplificador descrita en esta sección y de todos los amplificadores que comparten su topología es que es posible utilizar retroalimentación interna para proporcionar compensación fácilmente predicha y bien controlada. La compensación se implementa conectando una red entre los terminales marcados como compensación en la Figura 9.1. Esta red completa un bucle menor que incluye la etapa de alta ganancia. Dado que ambos polos dominantes del amplificador están incluidos dentro del bucle de retroalimentación local, es posible alterar la ubicación de los polos más importantes en la función de transferencia del amplificador mediante este tipo de retroalimentación interna. El grado de control que la retroalimentación de bucle menor puede ejercer sobre la función de transferencia de un amplificador de dos etapas se insinuó en la Sección 5.3 y en la discusión de los efectos\(C_{\mu}\) de la etapa de alta ganancia en la Sección 8.2.3.

Existen al menos dos limitaciones importantes para este tipo de compensación. Primero, dado que esta compensación es una forma de retroalimentación negativa, la magnitud de la función de transferencia del amplificador de bucle abierto compensada será menor o igual a la magnitud de la función de transferencia no compensada en la mayoría de las frecuencias. Si bien las resonancias introducidas por el bucle de retroalimentación menor pueden dar un aumento de ganancia en una o dos frecuencias particulares, el ancho de banda sobre el que existen tales aumentos está necesariamente limitado. En segundo lugar, existe alguna frecuencia máxima para la que se trata de un método efectivo de compensación, ya que más allá de esta frecuencia adquiere importancia la influencia de otras singularidades, algunas de las cuales están fuera del bucle compensador y por lo tanto no pueden controlarse. Si bien estas singularidades están todas a frecuencias comparables a las\(f_T\) de los transistores, sí establecen la última limitación de ancho de banda del amplificador debido al desplazamiento de fase que contribuyen a su función de transferencia de bucle abierto a frecuencias de interés. Por ejemplo, a 1/10 de su frecuencia de ruptura, un polo de décimo orden contribuye\(57^{\circ}\) de cambio de fase negativo a una función de transferencia pero solo cambia la magnitud en un 5%. En la práctica, la frecuencia de unidad-ganancia de la combinación amplificador-red de retroalimentación se elige normalmente para limitar la contribución de fase de las singularidades de alta frecuencia a\(30^{\circ}\) menos que a esta frecuencia para que la estabilidad no se vea comprometida. A menudo es necesario determinar la frecuencia a la que el desplazamiento de fase de las singularidades de orden superior adquiere importancia experimentalmente debido a las dificultades asociadas con la predicción analítica precisa de sus ubicaciones.

Figura 9.6 Modelo utilizado para ilustrar el método de compensación.

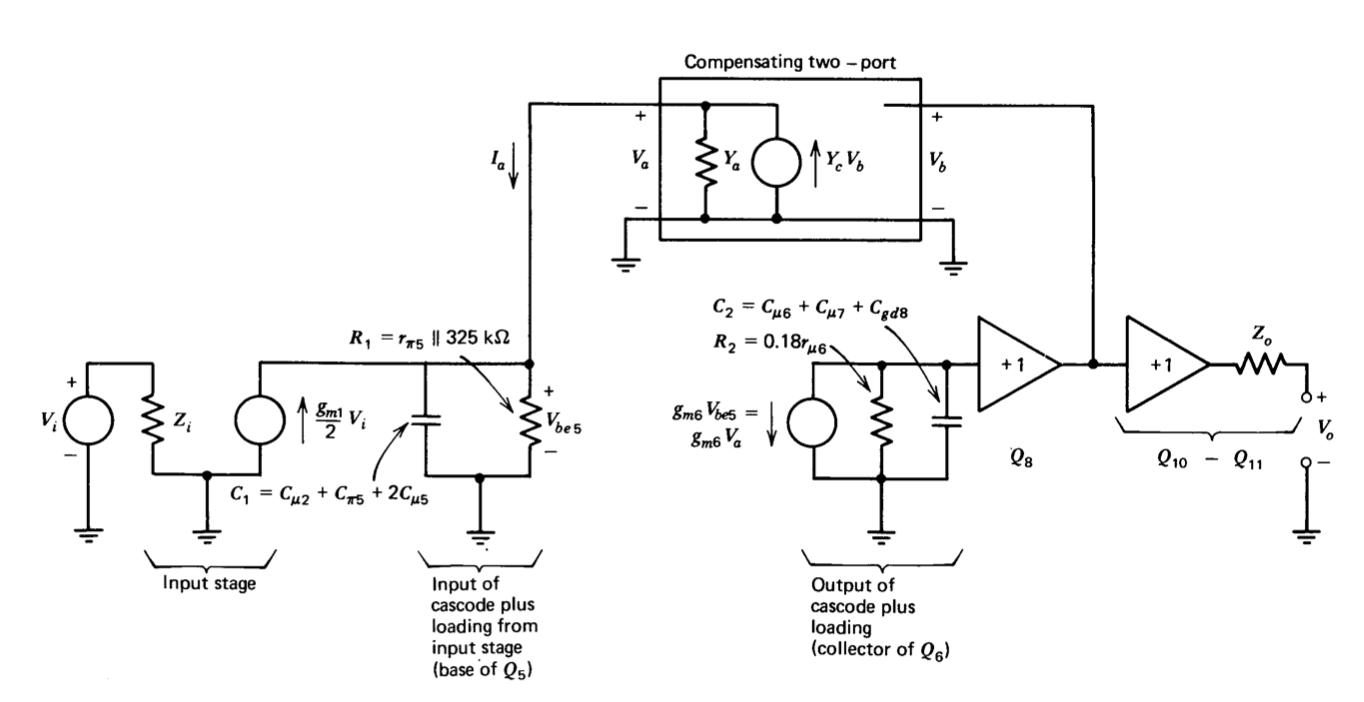
En la Figura 9.6 se muestra un modelo incremental para el amplificador de la Figura 9.1 que puede ser utilizado para analizar los efectos de la retroalimentación interna utilizada para la compensación. El desarrollo de este modelo se basa en gran medida en el análisis de la Sección 9.2.2. La impedancia de entrada del amplificador, que no es importante para los fines de este cálculo, es\(Z_i\). Un voltaje de entrada fuerza una corriente proporcional en el nodo incluyendo la base de\(Q_5\). (Esta representación asumió un voltaje de entrada aplicado a la entrada inversora del amplificador. Si se aplican voltajes a ambas entradas, se utiliza el voltaje diferencial para\(V_i\). Una ventaja de este tipo de amplificador es que la dinámica de la primera etapa no influye significativamente en la función de transferencia a frecuencias de interés; así funciona como un verdadero amplificador de entrada diferencial).

La impedancia en la base de\(Q_5\) se modela como una\(R-C\) red paralela con una constante de tiempo igual a\(\tau_b\) en Ecuación\(\ref{eq9.2.11}\). El resto del cascode se modela como una impedancia igual a la impedancia del colector de\(Q_6\) tierra impulsada por una fuente de corriente dependiente que suministra una corriente\(g_{m6} V_{be5}\). La transformación de impedancia del transistor de efecto de campo se resenta rep como un amplificador de búfer de ganancia de unidad de voltaje. El par emisor-seguidor complementario se modela como un segundo amplificador de búfer con una impedancia de salida\(Z_o\).

El bucle menor compensador se forma conectando una red de dos puertos entre la salida del seguidor de fuente y la base de\(Q_5\). Dado que el puerto derecho de la red es accionado por el seguidor de fuente de baja impedancia, el voltaje\(V_b\) es independiente de\(V_a\); así el puerto de dos puertos puede ser completamente representado en esta aplicación por las dos admitancias (Estas definiciones difieren de las utilizadas convencionalmente para describir dos puertos redes en que la dirección de referencia para\(I_a\) está fuera de la red. Esta elección reduce el número de signos menos en las siguientes ecuaciones.)

\[Y_a = -\dfrac{I_a}{V_a} \ \ \ V_b = 0 \nonumber \]

\[Y_c = -\dfrac{I_a}{V_b} \ \ \ V_a = 0 \nonumber \]

Las ecuaciones de nodo para el modelo de la Figura 9.6 son

\[\begin{array} {rcl} {\dfrac{g_{m1}}{2} V_i} & = & {(Y_1 + Y_a) V_a - Y_c V_b} \\ {0} & = & {g_{m6} V_a + Y_2 V_b}\label{eq9.2.15} \]

donde

\[Y_1 = \dfrac{1}{R_1} + C_1 s \nonumber \]

\[Y_2 = \dfrac{1}{R_2} + C_2 s \nonumber \]

Reconocer que el voltaje de salida\(V_o\) es idéntico a\(V_b\) en ausencia de carga nos permite determinar la ganancia del amplificador a partir de la ecuación\(\ref{eq9.2.15}\) como

\[\dfrac{V_o}{V_i} = \dfrac{V_b}{V_i} = -\dfrac{(g_{m1}/2) g_{m6}/[(Y_1 + Y_a) Y_2]}{1 + g_{m6} Y_c/[(Y_1 + Y_a) Y_2]}\label{eq9.2.16} \]

transmisión del bucle interno formado cuando se compensa el amplificador. En muchos casos de interés práctico, el ángulo de fase de esta expresión es cercano a más o menos\(90^{\circ}\) cuando su magnitud es la unidad. El margen de\(90^{\circ}\) fase del bucle compensador asegura entonces que no hay pico en su respuesta. En estos casos una aproximación muy simple sirve para determinar la magnitud de la función de transferencia de bucle abierto del amplificador, y la aproximación arroja un resultado que es correcto dentro de un factor de 0.707 en todas las frecuencias. La implicación de\(\ref{eq9.2.16}\) es que

\[\dfrac{V_o (j\omega)}{V_i (j\omega)} \simeq - \dfrac{g_{m1}}{2Y_c (j\omega )}\label{eq9.2.17} \]

en frecuencias donde

\[\left |\dfrac{g_{m6} Y_c (j\omega )}{[Y_1 (j\omega ) + Y_a (j\omega )] Y_2 (j\omega )} \right | > 1\nonumber \]

y

\[\dfrac{V_o (j\omega )}{V_i (j\omega )} \simeq -\dfrac{g_{m1}}{2} \dfrac{g_{m6}}{[Y_1 (j\omega ) + Y_a (j\omega )] Y_2 (j\omega )}\label{eq9.2.18} \]

en todas las demás frecuencias. Por lo tanto, cuando la magnitud de transmisión de bucle menor es grande, la función de transferencia de bucle abierto del amplificador es controlada por el elemento de retroalimentación de bucle menor.

Esta aproximación es particularmente fácil de aplicar gráficamente. La función de transferencia de bucle abierto del amplificador sin compensación, pero con la red compensadora cargando la base de\(Q_5\), se grafica en coordenadas log-magnitud vs. log-frecuencia. La carga adecuada se realiza conectando un lado de la red a la base de la\(Q_5\) manera habitual, y desconectando el otro lado de la red de la fuente de\(Q_8\) y conectándola en su lugar a una tierra incremental. Esta primera gráfica es particularmente fácil de obtener si se usa un solo condensador como elemento compensador (el caso más frecuente porque esta compensación conduce a una función de transferencia de bucle abierto aproximadamente de un solo polo) ya que solo\(\ref{eq9.2.12}\) se cambia la ubicación del polo de mayor frecuencia en la ecuación. La magnitud de la expresión también\(g_{m1}/2 Y_e(j\omega )\) se traza en las mismas coordenadas. La magnitud de la función de transferencia de bucle abierto del amplificador a cualquier frecuencia es entonces aproximadamente igual a la magnitud menor de las dos curvas trazadas. Esta relación se desarrolla fácilmente a partir de ecuaciones\(\ref{eq9.2.17}\) y\(\ref{eq9.2.18}\), al notar que la ganancia del amplificador con la red compensadora cortocircuitada conectada a la base de\(Q_5\) es

\[\dfrac{g_{m1}}{2} \dfrac{g_{m6}}{(Y_1 + Y_a) Y_2}\nonumber \]

y que si

\[\left | \dfrac{g_{m1}}{2Y_c} \right | < \left | \dfrac{g_{m1}}{2} \dfrac{g_{m6}}{(Y_1 + Y_a) Y_2} \right |\nonumber \]

entonces

\[\left | \dfrac{g_{m6} Y_c}{(Y_1 + Y_a) Y_2} \right | > 1\nonumber \]

Figura 9.7 Efecto de la compensación.

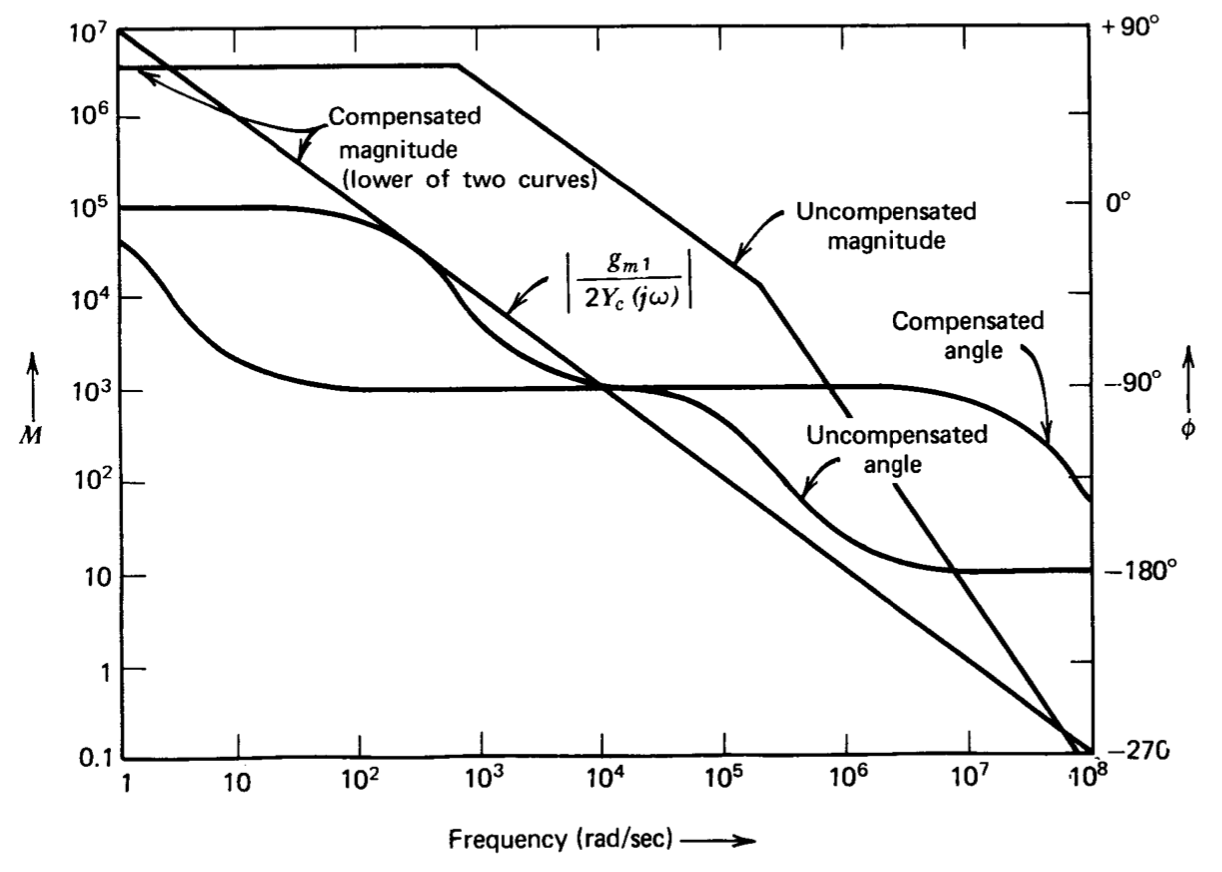
La Figura 9.7 ilustra los efectos de compensar el amplificador mostrado en la Figura 9.1 con un condensador de 20 pF. Las cantidades\(Y_c\) y\(Y_a\) para esta red compen sating son ambas iguales a\(2 \times 10^{-11}s\). Una de las dos curvas se obtiene directamente de la función de transferencia no compensada de la Figura 9.5 moviendo el segundo polo de\(2.2 \times 10^5\) radianes por segundo a\(1.5 \times 10^5\) radianes por segundo, ya que la carga por el condensador compensador aumenta la capacitancia total en la base de\(Q_5\) un 50%. La segunda parcela es

\[\left | \right | = \dfrac{10^7}{\omega } \nonumber \]

La curva para el amplificador compensado es la menor de las dos gráficas en todas las frecuencias.

Las ventajas de esta compensación para ciertas aplicaciones son obvias. Anteriormente se demostró que la operación con\(f = 1\) provocaría que oscilaría el amplificador no compensado. Si se utiliza un condensador compensador de 20 pF, el margen de fase del amplificador con realimentación directa es mayor que\(45^{\circ}\).

Tenga en cuenta que esta compensación reduce el polo de bucle abierto del primer amplificador a 2.5 radianes por segundo. La ubicación del polo de baja frecuencia no se puede elegir independientemente si insistimos en un rolloff unipolar a frecuencias

por debajo de la frecuencia de ganancia de unidad y limitar tanto la frecuencia de ganancia de unidad como la ganancia d-c. El polo debe estar ubicado a una frecuencia igual a la relación entre la frecuencia de ganancia unitaria y la ganancia d-c. Este polo no compromete el ancho de banda de bucle cerrado, ya que el ancho de banda de bucle cerrado está determinado por la frecuencia de cruce del bucle.

Vale la pena mencionar que los valores de los parámetros para este amplificador son tales que la función de transferencia de bucle abierto no compensada se modificará notablemente por cualquier compensación capacitiva superior a aproximadamente 0.1 pF! El valor mínimo del condensador necesario para modificar la función de transferencia del amplificador se puede determinar observando que la curva de magnitud no compensada que se muestra en la Figura 9.5 incluye una región donde su valor es\(2 \times 10^9/\omega \) Por lo tanto, si se usa un condensador superior a 0.1 pF para la compensación, la magnitud\([g_{m1}/2 Y_c(j\omega )\) será ser menor que la magnitud no compensada en algún rango de frecuencia. Además, es evidente que la retroalimentación de cualquier parte de alto nivel del circuito (desde el colector de\(Q_6\) encendido) de vuelta al circuito base de Q5 tiene aproximadamente el mismo efecto que la retroalimentación a través de los terminales de compensación. La inevitable capacitancia parásita entre estas dos partes del circuito suele ser del orden de 1 pF, por lo que se concluye que la curva “descompensada” de la Figura 9.7 probablemente nunca se pueda medir para un amplificador real.

Como se indicó anteriormente, la retroalimentación de cualquier porción del circuito desde el colector de\(Q_6\) on modifica el rendimiento de la misma manera que la retroalimentación desde la fuente de\(Q_8\), y en ciertas aplicaciones puede ser ventajoso compensar retroalimentando desde un punto alternativo. Por ejemplo, la retroalimentación del terminal de salida incluye más del amplificador dentro del bucle compensador y así con el control de este bucle. Desafortunadamente, la estabilidad del bucle de compensación es menos segura para este tipo de retroalimentación de bucle menor. De manera similar, si se utilizan capacitores grandes para la compensación, se puede lograr una mayor estabilidad del bucle interno compensando desde el colector\(Q_6\).

Algunas de las razones para seleccionar una topología de amplificador con la posibilidad de este tipo de compensación deberían quedar ahora claras. La compensación se elige normalmente para que, en lugar de la dinámica del amplificador no compensada, domine el rendimiento del amplificador en todas las frecuencias de interés. Por lo tanto, la función de transferencia de bucle abierto del amplificador con compensación se vuelve bastante confiable. Se puede obtener una amplia variedad de funciones de transferencia de bucle abierto (se darán varios ejemplos en el Capítulo 13) siendo la principal limitación el requisito de mantener la estabilidad del bucle compensador. Además, es fácil determinar qué red compensadora debe usarse para producir una función de transferencia de bucle abierto dada.