12.3: COMPUTACIÓN ANÁLO
- Page ID
- 84119
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Se mencionó en el Capítulo 1 que los amplificadores operacionales se utilizaron inicialmente principalmente para la computación analógica. El objetivo en la computación analógica es construir una red eléctrica, utilizando amplificadores operativos y
También se incluyen potenciómetros, y estos dispositivos se combinan con amplificadores de ganancia fija para proporcionar niveles de ganancia arbitrarios. Así, una ganancia de -3.12 podría realizarse precediendo un amplificador de ganancia de -10 con un potenciómetro establecido para una atenuación de 0.312. Con frecuencia se incluyen elementos no lineales como generadores de funciones y multiplicadores. Las entradas y salidas de los diversos elementos suelen estar conectadas a tomas de algún tipo. Las interconexiones necesarias para simular un sistema en particular se realizan luego con cables de conexión que conectan las diversas tomas. En muchos casos, la programación (insertando los patchcords para establecer el patrón de conexión adecuado) se realiza en una placa físicamente retirada de la computadora mientras que otros usuarios, con sus propias placas, resuelven sus problemas. La placa realiza las conexiones requeridas cuando se inserta en una placa de acoplamiento ubicada en la máquina.
Si bien la precisión de las soluciones obtenidas mediante computación analógica está limitada por las tolerancias de los componentes, normalmente supera con creces la precisión requerida para la simulación de sistemas físicos, que a su vez se construyen con componentes imprecisos. Una consideración adicional es que con frecuencia es posible obtener una buena sensación física para un sistema a través de la computación analógica, ya que muchas variables están disponibles para la observación, y dado que los efectos de las variaciones de parámetros pueden ser investigados rápidamente.
Nuestro tratamiento aquí solo puede cubrir lo esencial más básico y resaltar algunos de los circuitos auxiliares que se desarrollaron para la computación analógica. El lector interesado en un tratamiento detallado de esta fascinante y poderosa técnica es referido a Korn y Korn. (G. A. Korn y T. M. Korn, Computadoras Electrónicas Analógicas e Híbridas, 2ª Edición, McGraw-Hill, Nueva York, 1972.)
Enfoque
Nuestro objetivo aquí es mostrar cómo se utilizan técnicas electrónico-analógicas para simular ecuaciones diferenciales que describen los sistemas a estudiar. Inicialmente asumimos que la ecuación diferencial bajo investigación es lineal y tiene la forma general
\[a_n \dfrac{d^n x}{dt^n} + a_{n - 1} \dfrac{d^{n - 1} x}{dt^{n - 1}} + \cdots + a_1 \dfrac{dx}{dt} + a_0 x = f(t) \label{eq12.3.1} \]
Ciertamente no es necesario que la variable independiente del sistema en estudio sea el tiempo como lo implica la Ecuación\(\ref{eq12.3.1}\). Por ejemplo, si estuviéramos investigando la desviación de un puente bajo carga estática, podríamos estar interesados en desplazamientos verticales desde el equilibrio en función de la distancia desde un extremo del puente. Sin embargo, dado que nuestro análogo utilizará el tiempo como su variable independiente, sustituimos el tiempo por la variable independiente si es necesario en la ecuación original. De igual manera, nos damos cuenta de que cualquier variable dependiente en nuestro análogo tendrá que ser voltajes, independientemente de las variables que realmente representen en el sistema en estudio.
\(\ref{eq12.3.1}\)La ecuación se reescribe para que la derivada más alta de\(x\) se exprese en términos de las otras variables en la forma
\[\dfrac{d^n x}{dt^n} = -\dfrac{a_{n - 1}}{a_n} \dfrac{d^{n - 1} x}{dt^{n - 1}} - \cdots - \dfrac{a_1}{a_n} \dfrac{dx}{dt} - \dfrac{a_0 x}{a_n} + \dfrac{1}{a_n} f(t) \label{eq12.3.2} \]
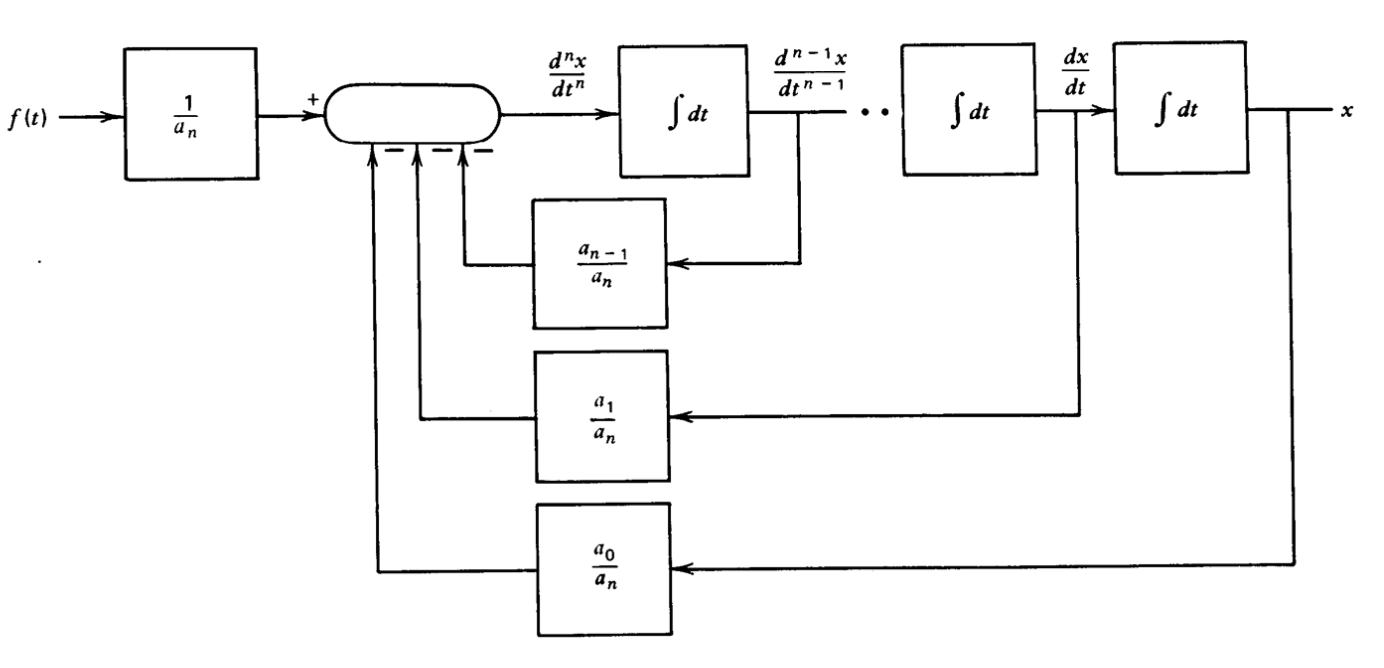
Figura 12.12 Diagrama de bloques de la Eqn\(\ref{eq12.3.2}\)
La ecuación se\(\ref{eq12.3.2}\) puede representar como el diagrama de bloques que se muestra en la Figura 12.12. En esta representación, la variable\(d^n x/dt^n\) aparece como la salida de un punto de suma. Las entradas al punto de suma son múltiplos escalados de la función de conducción y las derivadas de orden inferior de\(x\). Las derivadas de orden inferior se obtienen por integraciones sucesivas de\(d^nx/dt^n\), con un total de\(n\) integraciones requeridas para completar el diagrama de bloques.
Tenga en cuenta que los únicos elementos incluidos en el diagrama de bloques son un punto de suma de entrada múltiple, inversores que preceden a algunas entradas en el verano, bloques de ganancia e integradores. Dado que cada uno de estos elementos se puede construir fácilmente usando amplificadores operativos y componentes pasivos, el diagrama de bloques se puede implementar usando estos dispositivos. Cuando la realización analógica se excita con un voltaje igual a\(f(t)\), voltajes iguales en valor a\(x\) y sus derivados estarán disponibles como las salidas de los integradores.
Como ejemplo de este proceso, considere la ecuación diferencial
\[\dfrac{d^4 x}{dt^4} + 2.61 \dfrac{d^3 x}{dt^3} + 3.42 \dfrac{d^2 x}{dt^2} + 2.61 \dfrac{dx}{dt} + x = f(t) \nonumber \]
(Recordamos de la Sección 3.3.2 que esta ecuación representa un filtro Butterworth de cuarto orden). Resolviendo\(d^4 x/dt^4\) rendimientos
\[\dfrac{d^4 x}{dt^4} = - 2.61 \dfrac{d^3 x}{dt^3} - 3.42 \dfrac{d^2 x}{dt^2} - 2.61 \dfrac{dx}{dt} - x + f(t) \nonumber \]
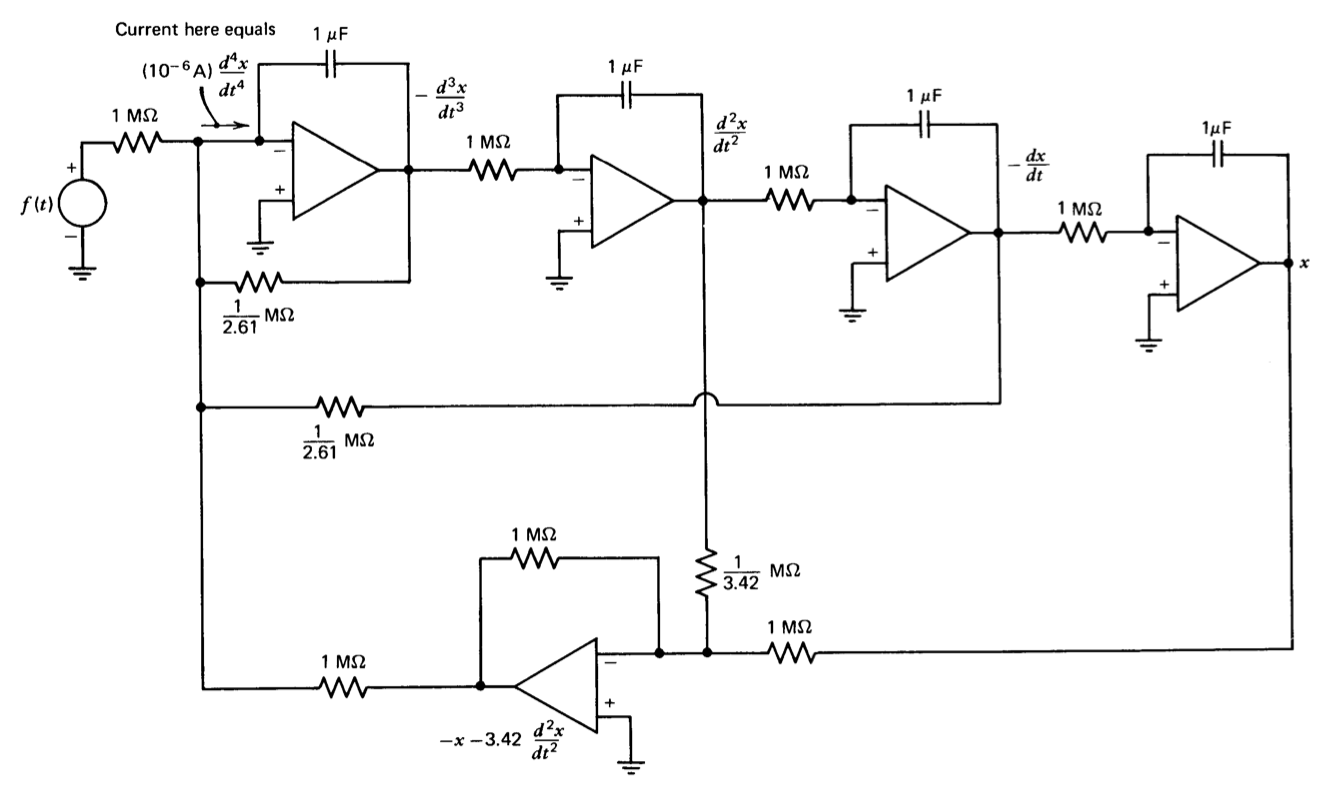
Una posible simulación de esta ecuación se muestra en la Figura 12.13. Los voltajes esperados en la salida de varios amplificadores se indican escribiendo el valor de la variable que representa la tensión en los nodos apropiados. Tenga en cuenta que en contraste con los métodos tradicionales analógico-computacionales, las ganancias se establecen seleccionando impedancias (Los niveles de impedancia relativa mostrados en la Figura 12.13 son altos si se utilizan amplificadores operacionales de propósito general como el LM101A. Dado que solo las relaciones son importantes para establecer la función de transferencia, todos los niveles de impedancia se pueden escalar para reducir los errores que resultan de las corrientes de entrada del amplificador.) utilizados alrededor de amplificadores operativos en lugar de combinar potenciómetros con amplificadores e integradores de ganancia fija. Además, se han combinado funciones con el fin de reducir el número de amplificadores requeridos. El uso de conexiones inversoras solo es tradicional en la computación analógica, y refleja el hecho de que una técnica de diseño de amplificador operacional utilizada frecuentemente para mejorar el rendimiento d-c da como resultado un amplificador que solo se puede usar en conexiones invertidas. (Ver Sección 12.3.3.) Por supuesto, puede ser posible utilizar integradores no inversores o amplificadores sumadores (realizados con suma resistiva en la entrada a una conexión de amplificador no inversor) si se utilizan amplificadores operacionales de propósito general para esta simulación.
Los cuatro integradores aparecen a lo largo de la parte superior del diagrama. Dado que se supone que no hay necesidad de tener\(d^4 x/dt^4\) disponible un voltaje que represente, la operación de suma se incluye en la primera conexión del integrador. La salida de este integrador es\(- (d^3x/dt^3)\) cuando la corriente indicada es igual a\((10^{-6}\ A) d^4x/dt^4\). Dado que se utilizan integradores inversores, se alternan los signos asociados a derivados sucesivos. El escalado y las inversiones requeridas por los coeficientes de\(x\) y su segunda derivada se obtienen con el amplificador inferior.
El número de amplificadores requeridos en la Figura 12.13 indica la regla general. Si se usa esta topología, la simulación de una ecuación diferencial lineal de\(n\) orden th requiere\(n\) integradores y un amplificador que invierta las señales apropiadas según sea necesario para completar las rutas de retroalimentación.
Las técnicas de computación analógica también se pueden usar para resolver una variedad de ecuaciones diferenciales no lineales al incluir hardware que implementa la no linealidad en la simulación. Como ejemplo, considere la ecuación diferencial de Van der Pol
\[\dfrac{d^2 x}{dt^2} + \mu (x^2 - 1) \dfrac{dx}{dt} + x = 0\label{eq12.3.5} \]
donde\(\mu\) es una constante positiva.
Para valores pequeños de\(x\), el coeficiente del primer término derivado es negativo, y el resultado de oscilaciones de amplitud creciente. Cuando la amplitud de la oscilación se vuelve lo suficientemente grande, el coeficiente de la primera derivada será positivo sobre parte del ciclo, y puede resultar un ciclo límite. \(\ref{eq12.3.5}\)La ecuación se reescribe en una forma conveniente para la simulación como
\[\dfrac{d^2 x}{dt^2} = -\mu x^2 \dfrac{dx}{dt} + \mu \dfrac{dx}{dt} - x\label{eq12.3.6} \]
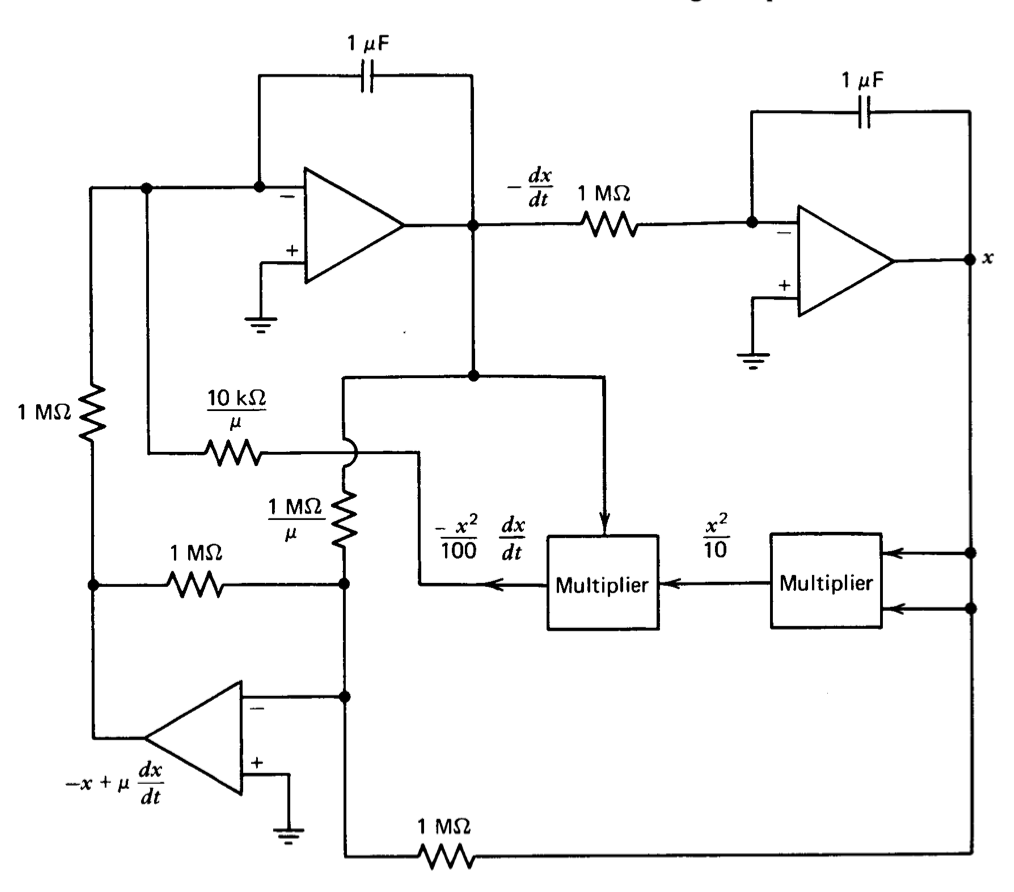
Se requieren multiplicadores para generar\(x^2\) y formar el\(x^2 (dx/dt)\) producto necesario para la simulación de Ecuación\(\ref{eq12.3.6}\). Dos técnicas para la multiplicación analógica se describieron en las Secciones 11.5.5 y 12.2.2. Los alicates múltiples prácticos basados en estos métodos a menudo están diseñados para tener un voltaje de salida igual al producto de los dos voltajes de entrada divididos por 10 voltios para compatibilidad con el rango dinámico de la mayoría de los amplificadores operativos de estado sólido. La Figura 12.14 muestra una posible simulación de Ecuación\(\ref{eq12.3.6}\) asumiendo que se utilizan multiplicadores con este factor de escala.
La ecuación de Van der Pol es un ejemplo de una ecuación diferencial no impulsada, y la excitación es solo por condiciones iniciales. Si bien no se mencionaron las condiciones iniciales en nuestra discusión anterior sobre la simulación de ecuaciones diferenciales lineales, reconocemos que debemos especificar las condiciones\(n\) iniciales para determinar la solución completa (homogénea más conducida) de una ecuación diferencial de\(n\) orden th. Estas condiciones iniciales se pueden establecer simplemente estableciendo los voltajes en los condensadores integradores en el momento\(t = 0\), ya que estos voltajes son proporcionales a los valores de\(x\) y sus primeras\(n - 1\) derivadas. Un circuito para establecer las condiciones iniciales se describe en la Sección 12.3.3.
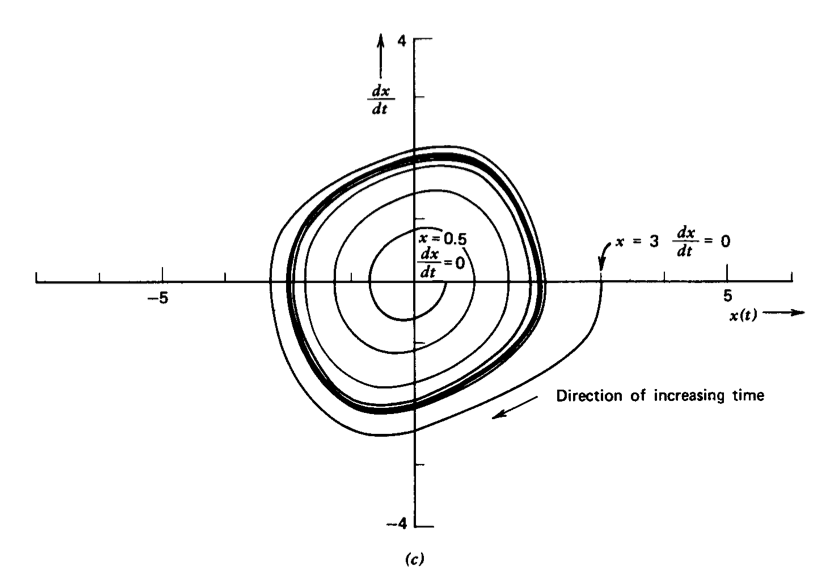
El valor de\(x\) como función del tiempo para la ecuación de Van der Pol con\(\mu = 0.25\) se muestra en la Figura 12.15. Las condiciones iniciales utilizadas para las partes\(a\) y\(b\) de esta figura son\(x(0) = 0.5, (dx/dt)(0) = 0\) y\(x(0) = 3, (dx/dt)(0) = 0\), respectivamente. Vemos que en ambos casos la amplitud del ciclo límite converge a un valor pico a pico de aproximadamente 4. Parte\(c\) de esta cifra es una gráfica de\(dx/dt\) versus\(x(t)\). Esta representación, en la que el tiempo es un parámetro a lo largo de la curva, se denomina gráfica de plano de fase. Se incluyen las respuestas para ambos valores de condiciones iniciales. La convergencia a ciclos límite de amplitud igual para ambos conjuntos de condiciones iniciales es evidente en esta figura.
El procedimiento formal aquí descrito no es ciertamente el único que da como resultado una correcta representación analógica de un problema. Si bien conduce a una realización compacta, otras realizaciones pueden mantener una mejor correspondencia con el sistema físico que se está modelando. Una técnica alternativa popular consiste simplemente en dibujar un diagrama de bloques para el sistema en estudio y luego implementar el diagrama de bloques bloque por bloque sin anotar nunca la ecuación diferencial completa del sistema. Si bien este enfoque a menudo requiere más hardware para completar la simulación, es conveniente ya que los voltajes proporcionales a las variables reales de interés en el problema en estudio están disponibles. Además, es generalmente posible utilizar esta alternativa para asociar factores de escala con los parámetros de los elementos físicos en los sistemas simulados sobre una base de uno a uno.
Amplitud y Escala de Tiempo
Consideraciones prácticas limitan la amplitud y rango de frecuencia de las señales que surgen en la computación analógica. Normalmente preferimos niveles máximos de señal que están cómodamente por debajo de los niveles de saturación del amplificador, pero muy por encima de las incertidumbres de ruido y compensación. Del mismo modo, las señales de muy baja frecuencia son difíciles de integrar con precisión, mientras que la ganancia limitada de un amplificador operacional a altas frecuencias compromete la precisión en este rango de frecuencias. El escalado de amplitud y el escalado de tiempo se utilizan para estandarizar las señales a niveles de amplitud convenientes y contenido espectral.
El escalado de amplitud implica poco más que algún esfuerzo adicional de contabilidad. Dado que estamos usando voltajes para todas las variables dependientes en nuestra simulación, debe haber un factor de escala dimensionado que relacione las variables de la máquina con las variables del problema cuando las variables del problema son cantidades distintas a los voltajes. Por ejemplo, si\(x\) es un desplazamiento en metros y algo de voltaje en una simulación representa esta variable sobre una base de 1 metro = 1 voltio, la variable de máquina realmente debería estar etiquetada (1 voltio/metro)\(x\) en lugar de simplemente\(x\) como se hace con frecuencia. Debemos darnos cuenta de que el número asociado con el factor de escala se puede seleccionar fácilmente para que sea distinto de la unidad. Así podríamos usar\(10x\) como etiqueta para algún voltaje, o, preferiblemente (10 voltios/metro)\(x\). Si este voltaje fuera de 7 voltios, el desplazamiento correspondiente sería\(x\) = (7 voltios) (1 metro/ 10 voltios) = 0.7 metro. Los valores apropiados para los factores de escala sólo se pueden determinar con un conocimiento de los niveles aproximados de problema-variable, ya que las variables correspondientes de la máquina deben tener valores pico ligeramente por debajo del nivel de saturación. Una vez seleccionados los factores de escala, se implementan modificando las ganancias de amplificadores e integradores a partir de sus valores inicialmente seleccionados.
El escalado de tiempo tiene ventajas más allá de las de centrar los componentes de frecuencia de señal dentro del rango de rendimiento óptimo del amplificador operativo. Consideremos, por ejemplo, la simulación de un problema de movimiento planetario que puede requerir años de “tiempo real” para completarse. El uso de una escala de “tiempo de máquina” más rápida nos permite obtener la solución en un intervalo de tiempo más razonable. De igual manera, el uso de un procedimiento de escalado más lento que en tiempo real nos permite visualizar la acumulación de carga en la región base de un transistor a una velocidad cómoda para su visualización en un osciloscopio de pantalla.
La técnica utilizada para el escalado de tiempo implica la sustitución
\[t = \sigma \tau \label{eq12.3.7} \]
donde\(\tau\) es el tiempo de máquina y es igual al tiempo real dividido por un factor de escala\(\sigma\). Un valor de a-mayor que uno implica que la solución de la máquina es más rápida que la solución real, por lo que un segundo de tiempo real está representado por un período\(\tau\) de tiempo de máquina más corto.
Este proceso se ilustra usando la forma para una ecuación diferencial dada en Ecuación\(\ref{eq12.3.1}\) y repetida aquí por conveniencia.
\[a_n \dfrac{d^n x}{dt^n} + a_{n - 1} \dfrac{d^{n - 1} x}{dt^{n - 1}} + \cdots + a_1 \dfrac{dx}{dt} + a_0 x = f(t) \nonumber \]
Para aplicar la sustitución de Ecuación\(\ref{eq12.3.7}\), cambiamos\(f(t)\) a\(f(\sigma \tau)\) y cambiamos\(d^m x/dt^m\) a\((1/\sigma^m)(d^m x/d\tau^m)\). Así, la versión escalada en el tiempo de la ecuación\(\ref{eq12.3.1}\) es
\[\dfrac{a_n}{\sigma^n} \dfrac{d^n x}{d\tau^n} + \dfrac{a_{n-1}}{\sigma^{n - 1}} \dfrac{d^{n - 1} x}{d\tau^{n - 1}} + \cdots + \dfrac{a_1}{\sigma} \dfrac{dx}{d\tau} + a_0 x = f(\sigma \tau) \nonumber \]
La ecuación cuando se simula tendrá una solución idéntica en forma a la de Ecuación\(\ref{eq12.3.1}\), pero ejecutará un factor de a-más rápido que la ecuación original.
Una segunda forma de implementar el escalado temporal es darse cuenta de que la dinámica de la simulación se implementa mediante integraciones, y que cambiar el factor de escala de cada integrador en la simulación por algún factor debe cambiar la escala de tiempo de la simulación precisamente por el mismo factor. Por lo tanto, los problemas pueden escalarse en el tiempo simulando primero el problema para una solución en tiempo real y luego dividiendo el valor de cada condensador por un factor de\(\sigma\). Alternativamente, cada resistencia utilizada para implementar todos los integradores puede reducirse en valor por un factor de\(\sigma\), o el cambio de factor de escala puede distribuirse entre resistencias y condensadores. El resultado neto de cualquiera de estas modificaciones será hacer que el problema en la máquina funcione un factor\(\sigma\) más rápido que la solución en tiempo real. Por supuesto, sigue siendo necesario aumentar la velocidad de las funciones de conducción aplicadas al sistema por un factor de\(\sigma\) si estas señales se derivan de fuentes que no se implementan utilizando integradores escalados.
Los coeficientes de la ecuación diferencial original a menudo se pueden utilizar para determinar la escala de tiempo apropiada a un problema particular. Si las raíces de la ecuación característica tienen magnitudes aproximadamente iguales, las frecuencias naturales de la solución no conducida serán del orden de
\[\omega = \left (\dfrac{a_0}{a_n} \right )^{1/n}\label{eq12.3.9} \]
Por el contrario, si el sistema está dominado por un polo, la frecuencia característica es del orden de
\[\omega = \dfrac{a_0}{a_1}\label{eq12.3.10} \]
Las frecuencias características dadas por Ecuación\(\ref{eq12.3.9}\) o se\(\ref{eq12.3.10}\) pueden cambiar a valores convenientes para la visualización y compatibles con el rendimiento del amplificador operativo mediante la selección apropiada de\(\sigma\).
Los valores de los elementos que ocurren en una simulación de problemas a menudo proporcionan claros indicios de la necesidad de modificar la amplitud o las escalas de tiempo. Si, por ejemplo, encontramos que se requiere una ganancia alta en la entrada de cada amplificador al que se le suministra alguna señal en particular, el factor de escala de esa señal es probablemente demasiado pequeño en relación con otros factores de escala de amplitud utilizados. Del mismo modo, si una resistencia de entrada a un amplificador sumador o un integrador es mucho mayor que todas las demás resistencias de entrada asociadas con el amplificador, la implicación es que el término aplicado a la entrada en cuestión aporta poco a la salida del sumador o integrador. En el caso de la selección de escala de tiempo, una elección inapropiada generalmente se refleja en valores de resistencia irrazonables, valores de condensadores o ambos asociados con integradores.
La ecuación de Van der Pol simulada antes (Eqn\(\ref{eq12.3.5}\)) se utiliza como un simple ejemplo de escala de tiempo y amplitud. Para el rango de condiciones iniciales utilizadas previamente y con\(\mu = 0.25\), las magnitudes máximas de\(x\) y\(dx/dt\) son aproximadamente 3 y\(3\text{ sec}^{-1}\), respectivamente, mientras que la magnitud máxima de\(d^2 x/dt^2\) es ligeramente mayor que\(3\text{ sec}^{-2}\). En consecuencia, si se asumen salidas de amplificador máximo de 10 voltios, son razonables factores de escala de 3 voltios por unidad para\(x\) y\(dx/dt\), combinados con un factor de escala de 2 voltios por unidad para\(d^2x/dt^2\). Si la ecuación\(\ref{eq12.3.6}\) se reescribe usando estos factores de escala, obtenemos
\[2 \dfrac{d^2 x}{dt^2} = -\dfrac{2}{27} \mu (3x)^2 \left (3 \dfrac{dx}{dt} \right ) + \dfrac{2}{3} \mu \left (3 \dfrac{dx}{dt} \right ) - \dfrac{2}{3} (3x) \label{eq12.3.11} \]
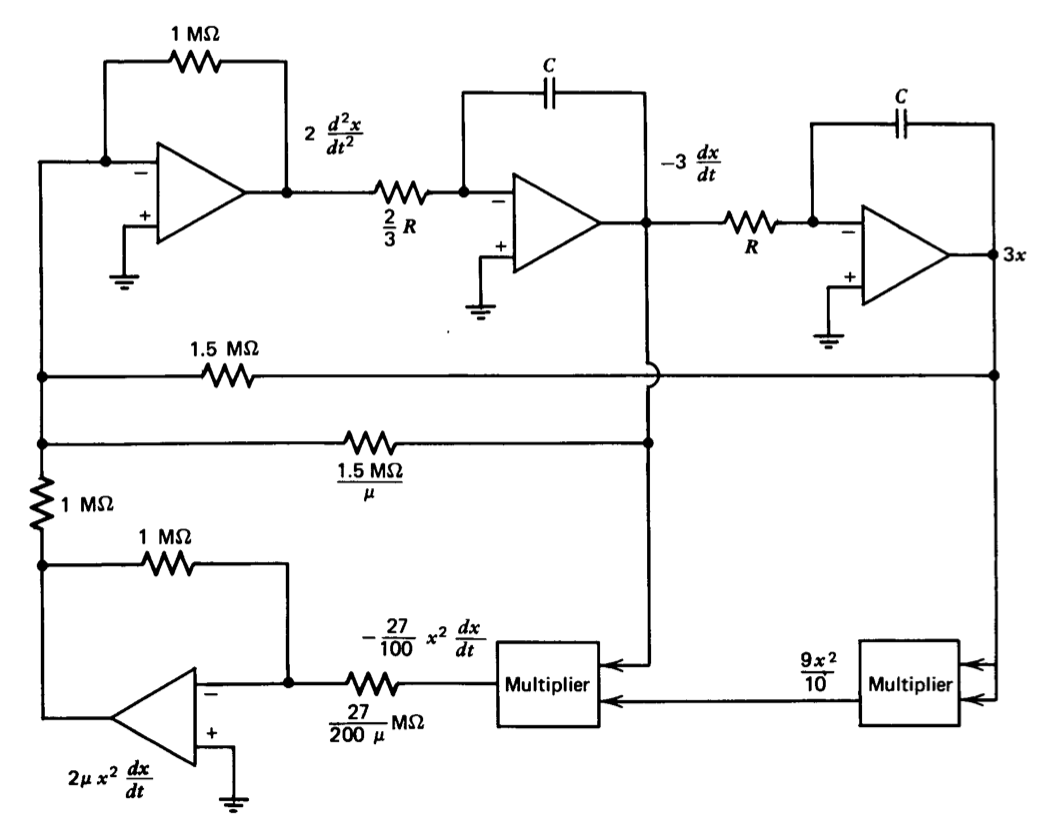
El diagrama de simulación, asumiendo nuevamente que se utilizan multiplicadores con salidas iguales al producto de las entradas divididas por 10, se muestra en la Figura 12.16. También se ha supuesto al formar este diagrama que\(d^2x/dt^2\) se requiere una tensión proporcional a. Tenga en cuenta que las señales de entrada aplicadas al primer amplificador son negativas del lado derecho de la Ecuación\(\ref{eq12.3.11}\) debido a la inversión asociada con este amplificador. La función de transferencia del primer integrador es\(-(3/2s)\) para que proporcione una salida de\(-3(dx/dt)\) cuando se acciona con\(2(d^2x/dt^2)\). El escalado alternativo puede ser advan tageous si\(\mu\) se utilizan diferentes valores de para mantener las magnitudes máximas de los voltajes proporcionales a\(dx/dt\) y\(d^2 x/dt^2\) en niveles óptimos.
Si se usa un valor de\(RC = 1\) segundo, la solución se ejecutará en tiempo real, y la frecuencia de oscilación será de aproximadamente un radián por segundo. Cambiar este producto escalará el tiempo de la solución. Por ejemplo, el uso de\(RC = 1\) ms da como resultado una oscilación de ciclo límite a aproximadamente 1000 radianes por segundo.
Circuitos auxiliares
Existen varias configuraciones de circuitos interesantes que se emplean frecuentemente en la computación analógica y que también se pueden usar en otras aplicaciones más generales.
Una de estas topologías es el integrador de tres modos. Hemos visto que es necesario aplicar condiciones iniciales a los integradores para obtener soluciones completas (homogéneas más impulsadas) para ecuaciones diferenciales simuladas. Otro modo de cálculo útil resulta si todos los integradores se conmutan simultáneamente a un estado en el que sus salidas se convierten en tiempo en variante y así mantienen los valores que estaban presentes en el momento de conmutación. Los valores de las variables problemáticas en el momento de la conmutación pueden entonces disuadirse de manera precisa con un voltímetro digital.
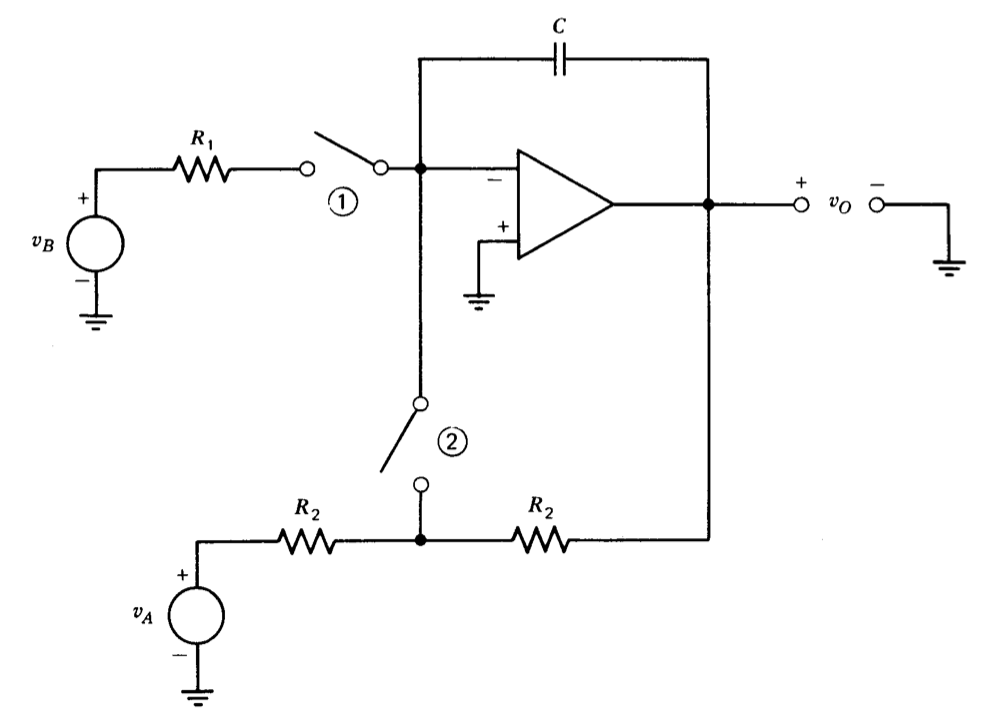
El integrador de tres modos mostrado en la Figura 12.17 permite la aplicación de condiciones iniciales y permite mantener una tensión de salida además de funcionar como integrador. Los modos de reinicio (o condición inicial), operación y retención se seleccionan mediante la elección apropiada de las posiciones del interruptor. Con el switch ① abierto y el switch ② cerrado, la función de transferencia de bucle cerrado del amplificador es
\[\dfrac{V_o (s)}{V_a (s)} = -\dfrac{1}{R_2 Cs + 1} \nonumber \]
Si\(v_A\) el tiempo es invariable en este modo, el condensador se cargará para que el voltaje de salida eventualmente se convierta en el negativo de\(v_A\). El voltaje del condensador puede entonces proporcionar condiciones iniciales para operaciones posteriores.
Si el switch ① está cerrado y el switch ② está abierto, el amplificador se integra de la\(v_B\) manera habitual.
Con ambos interruptores abiertos, la corriente del condensador se limita a la corriente de entrada del amplificador operacional y a la autofuga del condensador; así, el voltaje del condensador es idealmente invariable en el tiempo.
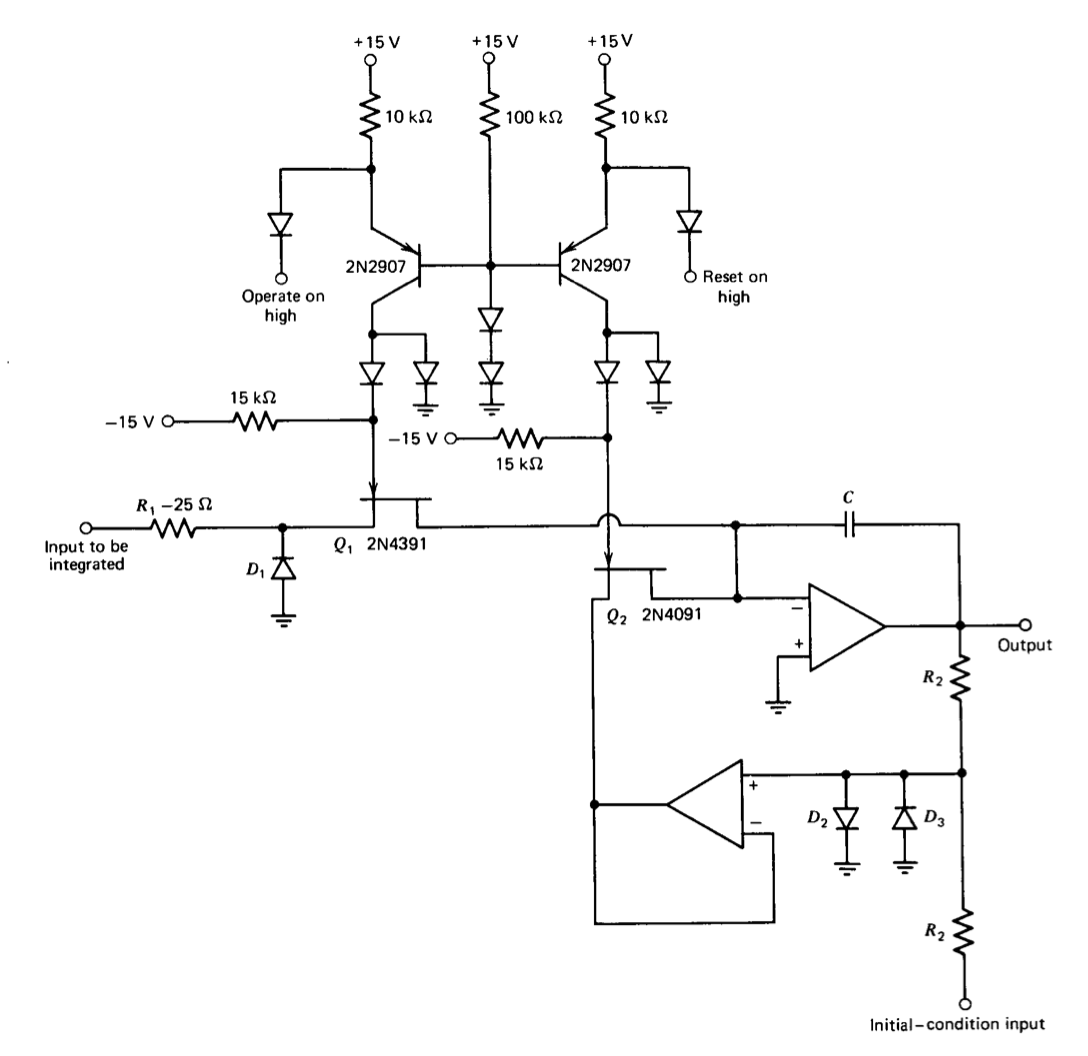
El tiempo de reinicio requerido de la conexión que se muestra en la Figura 12.17 puede ser bastante largo si se utilizan valores razonables para las resistencias etiquetadas\(R_2\). El uso de un segundo amplificador operacional conectado como seguidor de voltaje y que suministra un accionamiento de baja resistencia para la entrada inversora del integrador puede acortar sustancialmente los tiempos de reinicio. Un práctico circuito integrador de tres modos que incorpora esta característica se muestra en la Figura 12.18.
Los controladores de transistores bipolares son compatibles con señales\(T^2 L\) lógicas y conducen el potencial de puerta de los interruptores de transistor de efecto de campo a tierra en entradas que exceden dos voltajes directos de diodo. Con un nivel alto para la señal de “operar” y la señal de “reinicio” en tierra,\(Q_1\) está encendida y\(Q_2\) apagada. Esta combinación pone al circuito en el modo de integración normal. FET\(Q_1\) tiene una resistencia de drenaje a fuente de aproximadamente 25 ohmios, y este valor se compensa al reducir el tamaño de la resistencia de integración en un
cantidad correspondiente. \(D_1\)El diodo no conduce corriente significativa en este estado. Diodos\(D_2\) y\(D_3\) mantener la salida del seguidor dentro de aproximadamente 0.6 voltios de tierra. Un beneficio de esta sujeción es que la fuente de\(Q_2\) no puede llegar a ser lo suficientemente negativa como para iniciar la conducción con su puerta a - 15 voltios, ya que el voltaje máximo de pellizco del 2N4391 es de 10 voltios. El bloqueo del nivel de entrada del seguidor también mantiene sus niveles de señal cerca de los anticipados durante el reinicio, evitando así largos períodos de giro cuando el circuito se conmuta para aplicar las condiciones iniciales.
Con la puerta de\(Q_1\) a - 15 voltios (correspondiente a un nivel bajo en la línea de control “operar”), el diodo\(D_1\) evita potenciales de fuente que iniciarían la conducción del transistor\(Q_1\). Si\(Q_2\) está activado, el voltaje de salida se dirige hacia el negativo del nivel de señal de entrada en condición inicial. Los detalles del transitorio para un error grande dependen de las características del diodo, FET y amplificador. A medida que la señal de error se vuelve más pequeña, el bucle de reinicio ingresa a su región operativa lineal. El lector debe convencerse a sí mismo de que la transmisión de región lineal del bucle de reinicio (asumiendo amplificadores operativos ideales) es\(-1/2r_{ds} Cs\), donde\(r_{ds}\), es el drenaje-a-fuente incremental sobre la resistencia del FET. Así, la baja resistencia al FET, más que\(R_2\), determina la dinámica de la región lineal.
El modo de retención resulta con las señales tanto de “operar” como de “reinicio” en tierra para que ambos FET estén apagados. En este estado la corriente suministrada al condensador está determinada por la fuga de FET y la corriente de entrada del amplificador.
Una aplicación para este tipo de circuito además de su uso en computación analógica es como un circuito de muestreo y retención. En este caso el interruptor de operación no es necesario, y el circuito se conmuta de muestrear el negativo de una tensión de entrada para mantener con\(Q_2\).
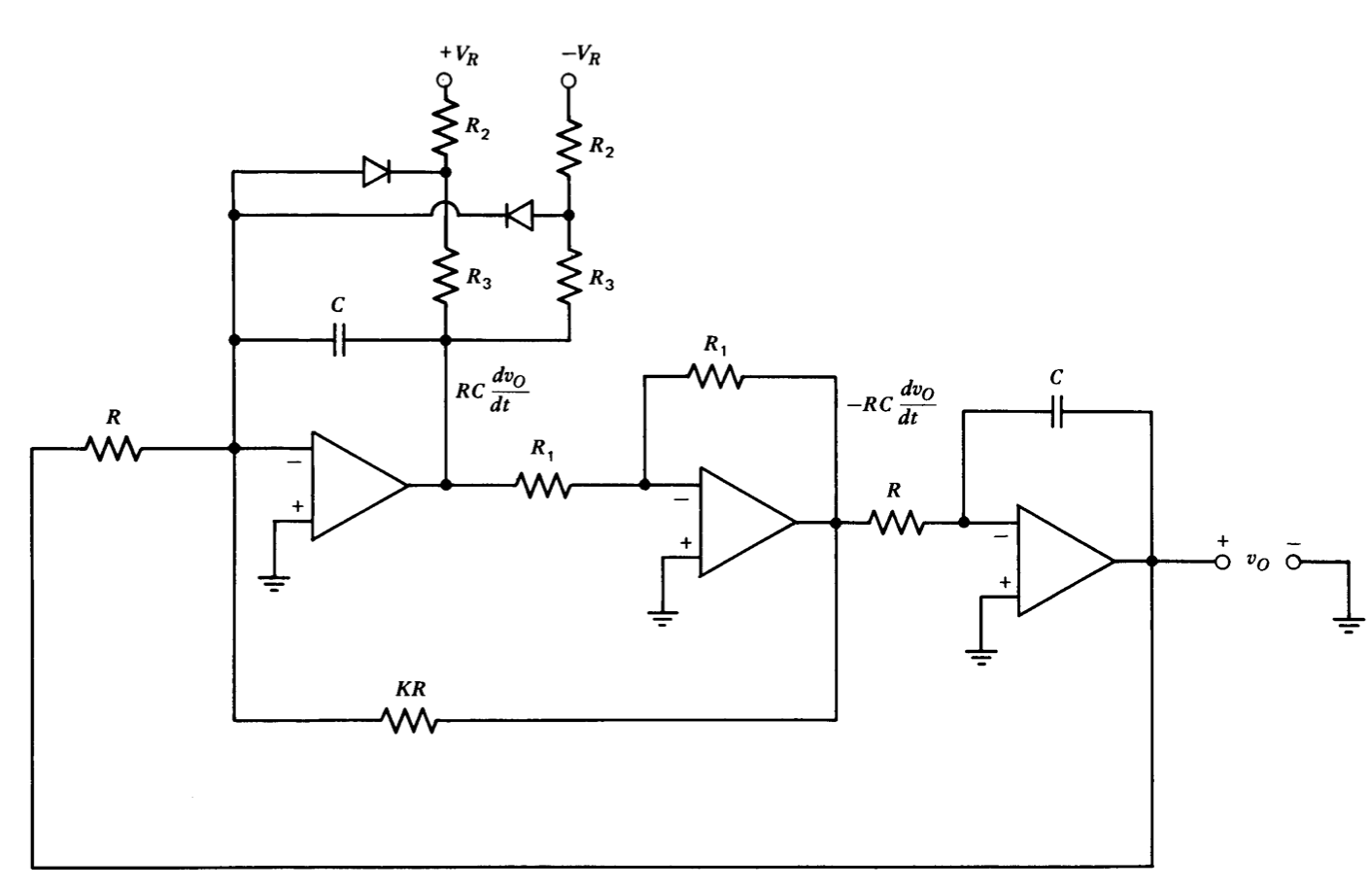
Las señales sinusoidales se utilizan frecuentemente como entradas de prueba en simulaciones analógico-computacionales. En la Figura 12.19 se muestra un oscilador en cuadratura que incluye limitación y que se ensambla fácilmente utilizando componentes disponibles en la mayoría de las computadoras analógicas. El diagrama implica una ecuación diferencial simulada, previa a la limitación, de
\[-R^2 C^2 \dfrac{d^2 v_O}{dt^2} = -\dfrac{RC}{K} \dfrac{dv_O}{dt} + v_O \nonumber \]
Reconocemos esta ecuación como una ecuación diferencial lineal de segundo orden con\(\omega_n = 1/RC\) y\(\zeta = - 1/2K\). El valor de\(K\) se elige lo suficientemente pequeño como para garantizar la oscilación con pérdidas anticipadas del condensador y las imperfecciones del amplificador, asegurando así que las amplitudes de señal serán determinadas principalmente por las redes de diodo-resistencia mostradas.
En muchas simulaciones se requiere una referencia de voltaje conocida con precisión para aplicar señales de entrada constantes, proporcionar voltajes de condición inicial, funcionar como un nivel de polarización para no linealidades o para otros fines. Las referencias de voltaje también se utilizan regularmente en una serie de aplicaciones no relacionadas con la simulación analógica.
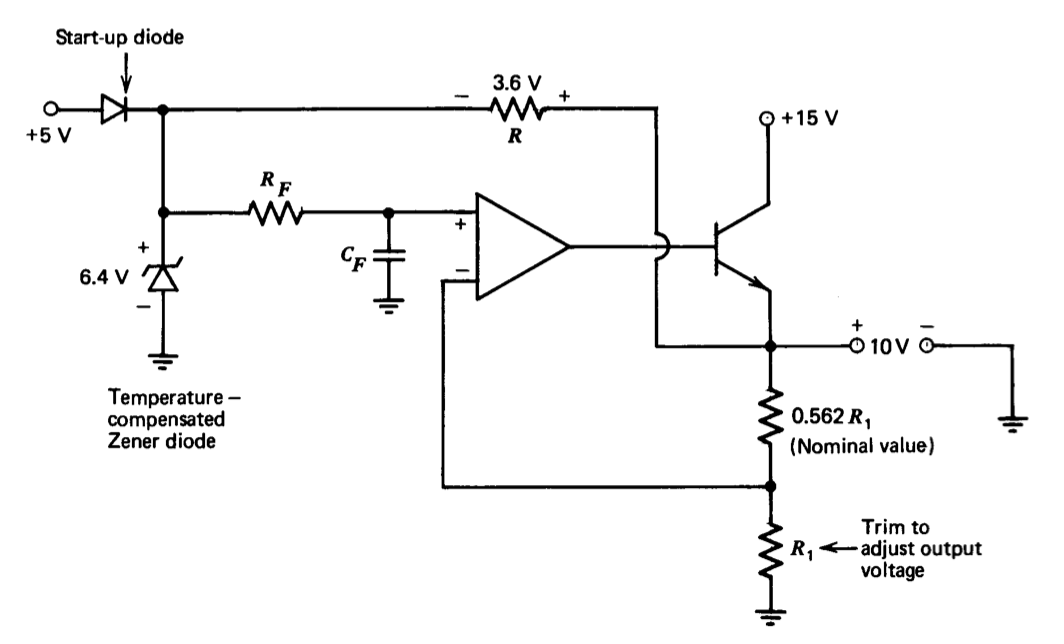
El circuito mostrado en la Figura 12.20 es una referencia de voltaje simple pero altamente estable. El amplificador operacional está conectado para una ganancia no inversora de un poco más de 1.5 de modo que se obtiene una salida de 10 voltios con 6.4 voltios aplicados a la entrada del amplificador no inversor.
Con la topología como se muestra, la tensión a través de la resistencia conectada desde la salida del amplificador a su entrada no inversora está restringida por la ganancia de bucle cerrado del amplificador a ser 0.562\(V_Z\) donde\(V_Z\) está la tensión directa del diodo Zener. La corriente a través de esta resistencia es la corriente de polarización aplicada al diodo Zener. La corriente de diodo Zener se establece así por el valor estable del voltaje Zener en sí. La resistencia de salida Zener no deteriora la regulación de voltaje ya que el diodo funciona a corriente constante en esta conexión. El filtro que sigue al diodo Zener ayuda a atentar las fluctuaciones de ruido en su voltaje de salida.
Se incluye un seguidor de emisor dentro del bucle operacional-amplificador para aumentar la capacidad de corriente de salida (los circuitos limitadores de corriente como se discuten en la Sección 8.4 suelen ser una precaución que vale la pena) y para reducir la impedancia de salida, particularmente a frecuencias más altas. Si bien la impedancia de salida de baja frecuencia del circuito sería pequeña incluso sin el seguidor debido a la retroalimentación, esta impedancia aumentaría a la impedancia de salida de bucle abierto del amplificador a frecuencias por encima del cruce. El seguidor del emisor reduce la impedancia de salida de bucle abierto para mejorar el rendimiento cuando se anticipan cambios de corriente de carga pulsados o de alta frecuencia. También se puede usar un condensador de derivación en la salida para reducir la impedancia de salida de alta frecuencia. (Ver Sección 5.2.2.)
El bootstrapping utilizado para excitar el diodo Zener es, por supuesto, una forma de retroalimentación positiva y deterioraría el rendimiento si la magnitud de esta retroalimentación se acercara a la unidad. La transmisión de baja frecuencia del bucle de retroalimentación positiva es
\[L = 1.562 \dfrac{r_d}{R + r_d} \label{eq12.3.14} \]
donde\(r_d\) está la resistencia incremental del diodo Zener. Esta expresión se evalúa usando parámetros para un 1N829A, un diodo Zener con compensación de temperatura. El diodo está diseñado para una corriente de funcionamiento de\(7.5\ mA\), y por lo tanto\(R\) será de aproximadamente 500\(\Omega\). La resistencia incremental del diodo se especifica como un máximo de 10\(\Omega\). Así la transmisión en bucle es, a partir de la Ecuación\(\ref{eq12.3.14}\), 0.03. Esta pequeña cantidad de retroalimentación positiva no afecta significativamente el rendimiento.
La retroalimentación positiva puede dar como resultado que el circuito funcione con el diodo en su estado de conducción directa en lugar de su modo de ruptura inversa normal. Este estado, que conduce a una salida negativa de aproximadamente un voltio, se puede eliminar con el diodo de arranque mostrado. El diodo de arranque asegura que el diodo Zener sea forzado a entrar en su región inversa, pero no contribuye a la corriente Zener en condiciones normales de funcionamiento.
Las imperfecciones esperadas del amplificador operacional tienen relativamente poco efecto en el rendimiento general del circuito de referencia. Un valor de 30,000 para la relación de rechazo de voltaje de suministro (típico de amplificadores de circuito integrado) provoca un cambio en el voltaje de salida de aproximadamente 50 AV por voltio de cambio de suministro. (Esta\(33\ \mu V/V\) sensibilidad es amplificada por la ganancia de bucle cerrado de 1.5.) La deriva de voltaje de entrada típica para muchos amplificadores operativos económicos es del orden de\(5\ \mu V\) por grado centígrado. Esta cifra no es significativa en comparación con el coeficiente de temperatura de 5 partes por millón por grado centígrado o aproximadamente\(32\ \mu V\) por grado centígrado de un diodo Zener de alta calidad como el 1N829A.
Los diseñadores de las grandes computadoras analógicas que evolucionaron durante el período comprendido entre principios de la década de 1950 y mediados de la década de 1960 a menudo dedicaron casi fanatical
esfuerzo para lograr una alta precisión estática en sus elementos de cómputos. Hacia este fin, los amplificadores operacionales se rodearon con resistencias enrolladas de alambre de alta precisión y capacitores que se podían recortar con precisión a los valores deseados. Estos componentes pasivos a menudo se colocaban en hornos de temperatura estable para eliminar las variaciones con la temperatura ambiente.
Los errores de baja frecuencia (particularmente el desplazamiento de voltaje de entrada) característicos de los amplificadores operacionales de tubo de vacío se eliminaron en gran medida por medio de una técnica imaginativa conocida como estabilización chopper. (E. A. Goldberg, “Estabilización de amplificadores de corriente continua de banda ancha para cero y ganancia”, Revisión RCA, Vol. II, No. 2, junio de 1950, pp. 296-300.) Este método
todavía se incorpora en algunos diseños modernos de amplificadores operativos, y proporciona una manera de reducir la deriva de voltaje y la corriente de entrada de un amplificador a niveles increíblemente pequeños. La implementación habitual de esta técnica puede ser vista como un ejemplo extremo de feedforward (ver Sección 8.2.2) y por lo tanto da como resultado un amplificador que solo puede ser utilizado en la inversión de conexiones.
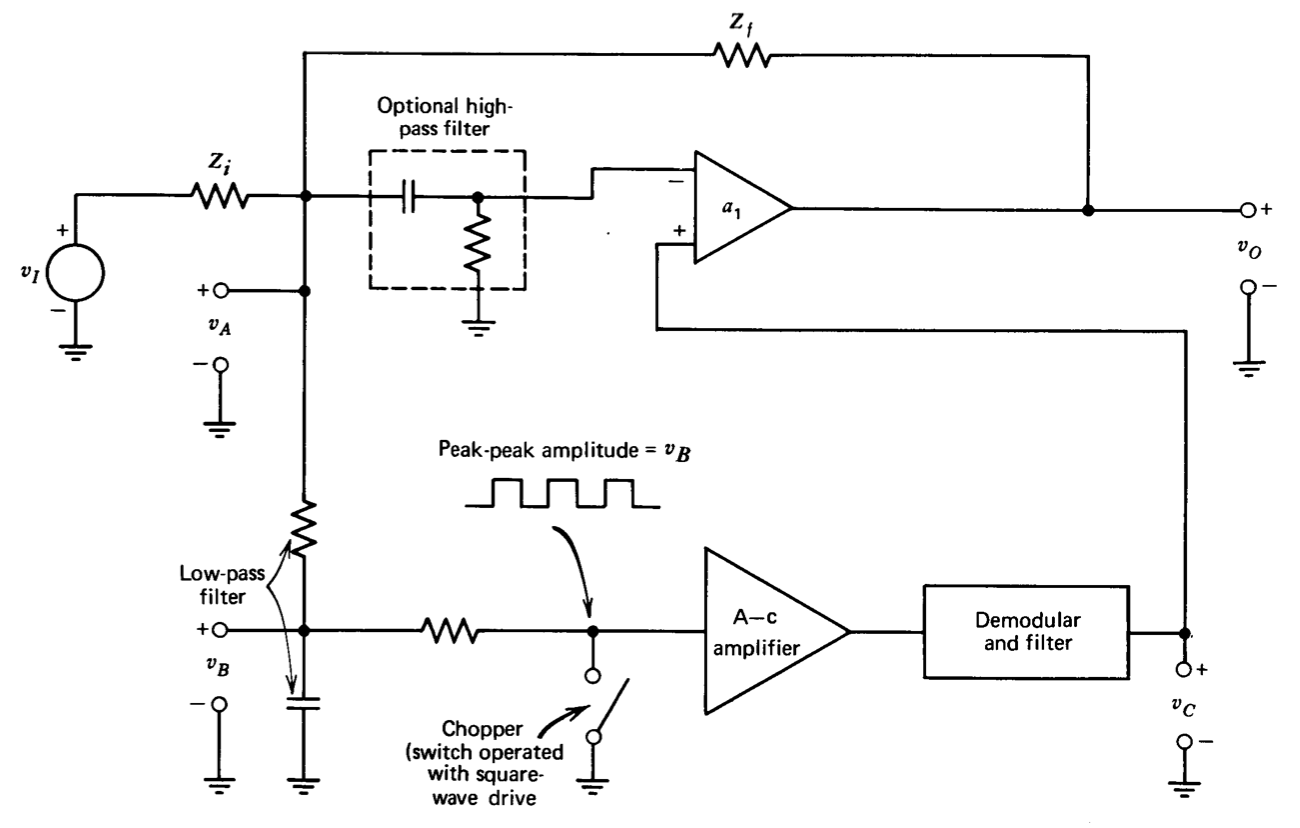
La Figura 12.21 ilustra el concepto. Supongamos que la red opcional se elimina de manera que la unión de\(Z_f\) y\(Z_i\) se conecta directamente a la entrada inversora del amplificador superior. La conexión resultante funciona claramente como un amplificador inversor si el voltaje\(v_C\) es cero. Observe que una condición necesaria para que la ganancia de bucle cerrado del amplificador sea igual a su valor ideal es esa\(v_A = 0\). El objetivo de la estabilización del helicóptero es reducir\(v_A\) a casi cero aplicando una señal apropiada a la entrada no inversora del amplificador superior.
El componente d-c del voltaje\(v_A\) se determina con un filtro de paso bajo, y este componente (\(v_B\)) se “corta” (se convierte en una onda cuadrada con amplitud pico a pico\(v_B\)) usando un interruptor operado periódicamente. (Los primeros diseños usaban interruptores mecánicos de láminas vibratorias, mientras que las unidades más modernas a menudo usan fotoresistencias iluminadas periódicamente o transistores de efecto de campo como interruptor). La señal a-c cortada puede amplificarse sin desplazamiento por un amplificador a-c y demodularse para producir una señal\(v_C\) proporcional a\(v_B\). Si la ganancia del amplificador a-c es alta, la ganancia de baja frecuencia\(v_C/v_A = a_{02}\) será alta. Si\(a_{02}\) es negativa, la señal aplicada a la entrada de ganancia positiva del amplificador superior será de la polaridad correcta para conducir\(v_A\) hacia cero. Los componentes d-c arbitrariamente pequeños de\(v_A\) pueden obtenerse teóricamente al tener una magnitud suficientemente alta para\(a_{02}\), aunque en la práctica los desplazamientos alcanzables están limitados por errores tales como voltajes inducidos térmicamente en el propio interruptor. El filtro paso bajo es necesario para evitar errores de muestreo que surgen si se aplican señales superiores a la mitad de la frecuencia de corte al picador.
Una forma alternativa de ver el funcionamiento de un amplificador estabilizado por interruptor es notar que las señales de alta frecuencia pasan directamente a través del amplificador superior, mientras que los componentes por debajo de la frecuencia de corte del filtro de paso bajo son amplificados tanto por el amplificador inferior como por el amplificador superior en cascada. (Es interesante observar que de esta manera se han logrado magnitudes de ganancia de bucle abierto de baja frecuencia superiores a 10). Por lo tanto, no es necesario aplicar señales de baja frecuencia directamente al amplificador superior, y se puede incluir un filtro de paso alto (mostrado como la red opcional) en serie con la entrada inversora del amplificador superior. Como resultado, tanto la compensación de voltaje como la corriente de entrada al amplificador operacional se pueden reducir mediante la estabilización del interruptor, lo que produce un amplificador con características de baja frecuencia prácticamente ideales.
Varios fabricantes ofrecen paquetes que combinan choppers de componentes discretos con amplificadores de circuito integrado. Más recientemente, los fabricantes de circuitos integrados han podido fabricar amplificadores completos estabilizados por interruptor, ya sea en forma monolótica o combinando varios chips monolíticos para formar un circuito híbrido. Estos circuitos incorporan mejoras topológicas que permiten un verdadero funcionamiento diferencial. Los condensadores grandes requeridos están conectados externamente al paquete. Derivas de una fracción de microvoltio por grado centígrado, junto con corrientes de entrada en el rango de picoamperios, están disponibles a un costo sorprendentemente bajo.


