2.5: Potencia y eficiencia

Los términos poder y energía a menudo se usan incorrectamente como sinónimos. Aunque relacionados, no son lo mismo. Como ya se mencionó, la energía es la capacidad de hacer trabajo. En contraste, la potencia es la tasa de consumo de energía. La potencia se denota con la letra\(P\) y tiene unidades de watts, aunque a veces se utilizan otras unidades como la potencia (1 caballo de fuerza\(\approx\) 746 watts). Un vatio se define como un joule de energía consumida por segundo.

\[1 \text{ watt } \equiv 1 \text{ joule } / 1 \text{ second } \label{2.5} \]

Como fórmula,

\[P = W / t \label{2.6} \]

Dónde

\(P\)es la potencia en vatios,

\(W\)es la energía en julios,

\(t\)es el tiempo en segundos.

Para entender mejor el concepto, considera por un momento un delicioso sándwich de mantequilla de maní y plátano. Este sándwich contiene cierto número de calorías de los alimentos, digamos 300 en total. Una caloría alimentaria se refiere a una cierta cantidad de energía que los humanos pueden extraer de un elemento de alimento. Esa energía nos permite hacer algún tipo de trabajo como caminar, nadar o simplemente respirar. El sándwich puede verse como un medio de almacenamiento de energía, una batería para unidades biológicas llamadas humanos. La pregunta es, ¿qué hacemos con la energía, y más al grano, qué tan rápido la usamos? Por ejemplo, ese sándwich podría ser suficiente para permitir que alguien corra una carrera en carretera de 5k (3.1 millas) en 17 minutos. En contraste, también podría ser suficiente para permitir que esa misma persona vea televisión durante tres horas. Es la misma cantidad de energía que se está usando, solo se está utilizando a un ritmo mucho más rápido en el primer caso. Esa tasa es poder. El corredor de 5k tiene una salida de potencia mucho mayor que el observador de TV.

Ejemplo 2.5.1

100 julios son consumidos por un dispositivo en 0.1 segundos. Determine la potencia en vatios y en caballos de fuerza.

\[P = \frac{W}{t} \nonumber \]

\[P = \frac{100 J}{0.1s} \nonumber \]

\[P = 1000 W \nonumber \]

Como un caballo de fuerza es aproximadamente 746 vatios, esto equivale a

\[P_{hp} = \frac{P_W}{746W/hp} \nonumber \]

\[P_{hp} = \frac{1000 W}{746W/hp} \nonumber \]

\[P_{hp} = 1.34 hp \nonumber \]

La potencia también se puede encontrar multiplicando una corriente por la tensión asociada. Para comenzar, observamos las definiciones de corriente y voltaje, Ecuaciones 2.3.2 y 2.4.2 respectivamente, y luego las combinamos.

\[I = \frac{Q}{t} \nonumber \]

\[V = \frac{W}{Q} \nonumber \]

\[I \times V = \frac{Q}{t} \times \frac{W}{Q} = \frac{W}{t} \nonumber \]

De la Ecuación\ ref {2.6}, lo sabemos\(P = W/t\), así\(P = IV\). Esto se conoce como ley de poder.

\[P = I \times V \label{2.7} \]

Dónde

\(P\)es la potencia en vatios,

\(I\)es la corriente en amperios,

\(V\)es el voltaje en voltios.

Ejemplo 2.5.2

Si una batería de 9 voltios entrega una corriente de 0.1 amperios, determine la potencia entregada en vatios.

\[P = I \times V \nonumber \]

\[P = 0.1amps \times 9volts \nonumber \]

\[P = 0.9W \nonumber \]

Eficiencia

La eficiencia es la relación entre la potencia de salida útil y la potencia aplicada expresada como porcentaje. Se denota con la letra griega\(\eta\) (eta) y siempre es inferior al 100%. Expresado como una fórmula,

\[\eta = \frac{P_{out}}{P_{in}} \times 100 \% \label{2.8} \]

Dónde

\(\eta\)es la eficiencia en porcentaje,

\(P_{out}\)es la potencia de salida,

\(P_{in}\)es la potencia de entrada.

En términos generales, cuanto mayor sea la eficiencia, mejor. Esto implica menos desperdicio. En otras palabras, si un sistema es 30% eficiente, entonces 70% de la potencia de entrada se desperdicia, mientras que si un sistema es 99% eficiente, entonces solo se desperdicia 1% de la potencia de entrada. El concepto se ilustra gráficamente en la Figura 2.5.1 . En la mayoría de los sistemas, la energía residual se convierte en calor que no es un producto deseado y, de hecho, a menudo reduce la vida útil de los componentes eléctricos.

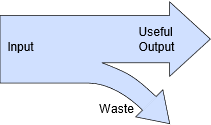
Figura 2.5.1 : Concepto básico de eficiencia.

Ejemplo 2.5.3

Si un dispositivo consume 200 vatios de potencia y tiene una salida útil de 120 vatios, determine la eficiencia.

\[\eta = \frac{P_{out}}{P_{in}} \times 100 \% \nonumber \]

\[\eta = \frac{120W}{200W} \times 100 \% \nonumber \]

\[\eta = 60 \% \nonumber \]

En este caso, el dispositivo está desperdiciando el 40% de la potencia de entrada, o 80 vatios.

Ejemplo 2.5.4

Un amplificador de audio tiene una salida nominal máxima de 100 vatios a un altavoz. Si exhibe una eficiencia del 70%, determine la potencia de entrada requerida y la cantidad de energía desperdiciada.

\[\eta = \frac{P_{out}}{P_{in}} \times 100 \% \nonumber \]

\[P_{in} = \frac{P_{out}}{\eta} \times 100 \% \nonumber \]

\[P_{in} = \frac{100W}{70 \%} \times 100 \% \nonumber \]

\[P_{in} = 142.9 watts \nonumber \]

Como el amplificador dibuja 142.9 vatios y solo se entregan 100 vatios al altavoz, entonces la diferencia, o 42.9 vatios, es la potencia desperdiciada (muy probablemente solo haciendo que el amplificador esté caliente).