3.2: Flujo de corriente convencional y flujo de electrones

Antes de sumergirnos en los circuitos en serie debemos considerar una pregunta interesante que involucra la dirección del flujo de corriente. ¿Fluye de positivo a negativo o de negativo a positivo? Para el caso, ¿incluso marca la diferencia en lo que respecta a nuestros análisis?

Benjamin Franklin (representado en la Figura 3.2.1 ) comenzó a experimentar con el fenómeno de la electricidad en 1746. En 1752 realizó su famoso experimento de cometas demostrando que el rayo es una forma de electricidad al capturar la carga de las nubes de tormenta en una jarra leyden (una forma temprana de un dispositivo de almacenamiento de carga eléctrica) ¹. En este momento no existía el concepto moderno de un modelo atómico con electrones y protones y la electricidad se concibió como una especie de fluido. Franklin supuso que el “flujo eléctrico” pasó de positivo a negativo. Esta idea fue aceptada y se convirtió en la visión convencional. Hoy llamamos a esta idea flujo de corriente convencional. En este modelo, la corriente fluye de una tensión más positiva a una tensión menos positiva. Ahora sabemos que el electrón es el portador de carga en los metales y los electrones viajan en la dirección inversa. Esencialmente, Franklin adivinó mal. Los electrones pasan de un potencial menor a un potencial mayor. A este modelo le llamamos flujo de electrones. Para la mayoría de los trabajos, los ingenieros y técnicos utilizan el flujo convencional, aunque en algunos casos, como la explicación de los semiconductores, el flujo de electrones es más fácil de visualizar para algunas personas. En definitiva, el flujo convencional existe por razones históricas, y es el modelo utilizado para la mayoría de los análisis, incluido este texto.

Figura 3.2.1 : Benjamin Franklin: Técnicamente incorrecto pero realmente no importa.

Se podría pensar que la dirección actual marcaría una gran diferencia en un análisis; después de todo, ciertamente hace una gran diferencia si conduces un automóvil en la dirección equivocada. Resulta que ambas formas lograrán los resultados deseados, solo tenemos que ser consistentes con el uso.

Para entender mejor esto, considere que el movimiento de una carga negativa neta en una dirección puede considerarse como un movimiento de una carga positiva neta en la otra dirección. Es decir, el movimiento de un electrón crea un “agujero” donde solía estar y ese agujero es neto positivo. Esto se ilustra en la Figura 3.2.2 . Aquí partimos en la parte superior con un tubo de mármoles idénticos, todos empujados hacia la derecha. En cada paso por debajo de él movemos una canica hacia la izquierda, imitando el flujo de electrones en un circuito. Al llegar al fondo, cada mármol ha sido empujado a la izquierda por un lugar. También podemos llegar al dibujo inferior simplemente tomando el mármol más a la derecha en el dibujo superior e insertándolo al extremo izquierdo saltando sobre las otras tres canicas. Aquí está lo importante: en lugar de imaginar las canicas moviéndose hacia la izquierda, también podemos pensar en términos de “espacio negativo” e imaginar la ranura vacía moviéndose hacia la derecha. Eso es flujo de agujeros. Los dos puntos de vista son funcionalmente idénticos ya que conducen al mismo resultado.

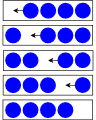
Figura 3.2.2 : Flujo de electrones versus agujero.

Referencias

¹ Cabe señalar que la cometa de Franklin no fue alcanzada por un rayo. Si lo hubiera sido, probablemente habría sido asesinado. La cuerda de cáñamo que se utilizó para la cometa estaba suficientemente húmeda por la lluvia como para que fuera posible transferir la carga de la atmósfera a la jarra leyden, y posteriormente a una llave metálica que emitiría una chispa.