3.3: La conexión en serie

Última actualización
Guardar como PDF

Page ID: 85993

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

La palabra circuito proviene de la raíz latina circ, que significa “anillo” o “alrededor”. Un circuito eléctrico consiste en al menos un anillo o bucle a través del cual fluye la corriente. Por ejemplo, si tenemos una batería conectada a una lámpara como en la Figura 3.3.1 , la corriente sale de la batería, fluye a través de la lámpara, y luego regresa al otro lado de la batería creando un bucle o circuito terminado. Sin un camino de regreso a la batería, la corriente no fluirá. Así, si cortamos uno de los cables que conectan la batería y la lámpara, no hay trayectoria para la corriente y no fluye corriente. Esto se conoce como un circuito abierto y es una falla común que ocurre cuando los sistemas electrónicos se caen o golpean con fuerza. Obviamente, esto tenderá a dejar inutilizable el circuito. En este ejemplo, la lámpara no se iluminará. Lo opuesto al circuito abierto es el cortocircuito. En un cortocircuito, existe una ruta alternativa no intencionada para el flujo de corriente y esto también puede crear un mal funcionamiento. En el caso de nuestra batería y lámpara, puede ocurrir un cortocircuito si un trozo de alambre o metal cae accidentalmente a través de los terminales de la lámpara. La corriente tendría entonces una trayectoria de alta conductancia (es decir, baja resistencia) alrededor de la lámpara. La gran mayoría de la corriente tomaría esta trayectoria de baja resistencia en lugar de la trayectoria de mayor resistencia que presenta la lámpara. El resultado sería que la lámpara no se encendería. Ya sea en el caso abierto o corto, la luz no funciona pero hay una diferencia importante: para el cortocircuito, saldrá corriente excesiva de la batería porque hay poco para resistir el flujo de corriente. De esta manera, la batería se agotará muy rápidamente. Para el abierto, no fluye corriente y por lo tanto la batería no se drena.

Figura 3.3.1 : Circuito de batería y lámpara.

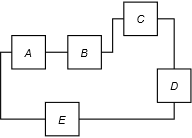
Figura 3.3.2 : Una configuración de serie genérica.

Las conexiones en serie no se limitan a solo dos componentes. En general, una conexión en serie es cualquier conexión de componentes configurados de tal manera que la corriente a través de cada componente debe ser la misma. Esto se ilustra en la Figura 3.3.2 . Dentro de cada una de las cajas con letras habría un componente como una resistencia o una fuente de voltaje. Tenga en cuenta que para cada componente, hay un punto de entrada y un punto de salida. No importa qué caja elija, la corriente que fluye a través de ella debe ser la misma que la corriente que fluye hacia la siguiente caja o fuera de la caja anterior, y no importa si sigue este camino en sentido horario o antihorario. Por lo tanto, toda esta configuración es una conexión en serie. La idea de que la corriente es consistente a lo largo de todo debe ser autovisible. Después de todo, la única forma en que la corriente a través, digamos, el ítem B podría ser diferente de la que fluye a través del ítem C o D es si parte de ella de alguna manera “desapareció” en el camino por arte de magia. Es importante recordar que la corriente consistente es la característica distintiva que define una conexión en serie:

\[\text{The current is the same everywhere in a series connection.} \label{2.1} \]

Es posible que solo una parte de un circuito exhiba una conexión en serie. Considera el diagrama más complejo que se presenta en la Figura 3.3.3 . Algunos de estos artículos están en serie y otros no. Por ejemplo, los ítems A y B están en serie entre sí pero no en serie con los elementos restantes. ¿Por qué? Porque si imaginamos que la corriente fluye a través de A y luego a través de B deben ser las mismas, sin embargo, una vez más allá de B, la corriente podría dividirse y fluir hacia abajo por otras ramas: una porción que entra en C, una porción que ingresa a D y el resto fluye hacia E. Por otro lado, los ítems C y F están en serie entre sí porque cualquiera que sea la corriente que fluye a través de una de ellas debe estar fluyendo por la otra. Así, los ítems A y B están en serie entre sí y los ítems C y F están en serie entre sí, aunque los cuatro no están en serie como grupo.

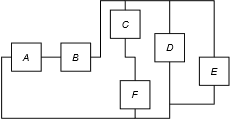
3.3.3 : Una configuración más compleja.

Es posible que no haya dos elementos en un circuito estrictamente en serie. Veremos ejemplos de esto en los próximos capítulos. Además, el hecho de que las corrientes a través de dos ítems pasen a ser las mismas, eso no significa necesariamente que estén en serie. Corrientes idénticas podrían ser solo un subproducto de los valores de los componentes elegidos. Por ejemplo, aunque los ítems D y E de la Figura 3.3.3 tengan el mismo valor numérico para current, no diríamos que están en serie, más de lo que diríamos que dos personas cualesquiera con el mismo apellido tendrían que ser hermanos.