3.5: Ley de Ohm
- Page ID
- 85988
En el Capítulo 2, se introdujo el concepto de resistencia utilizando la siguiente generalidad:
\[Effect = \frac{Cause}{Oppostion} \nonumber \]
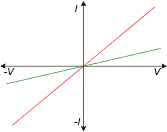
Figura 3.5.1 : Gráfica de corriente-voltaje para resistencias simples.
Para revisar, la causa es una fuente de voltaje, la oposición es la resistencia, y el efecto es la corriente resultante. Si el elemento por el que pasa la corriente es lineal, como las resistencias simples representadas en la Figura 3.5.1 , entonces esta relación se puede reescribir como:
\[I = \frac{V}{R} \nonumber \]
o más comúnmente, resuelto para el voltaje y expresado como:
\[V = I \times R \label{3.3} \]
Esto se llama ley de Ohm, y se nombra en honor a Georg Ohm, un investigador de principios del siglo XIX. Es, junto con las leyes de Kirchhoff que veremos en breve, una de las ecuaciones más importantes y útiles disponibles para el análisis de circuitos eléctricos de CC. En aras de la integridad, la ley de Ohm también se puede visualizar en términos de resistencia:
\[R = \frac{V}{I} \nonumber \]
Las tres formas de esta ecuación son útiles. Por ejemplo, podemos usar la primera versión si tenemos un voltaje conocido aplicado a través de una resistencia y queremos determinar la corriente resultante. Del mismo modo, la Ecuación\ ref {3.3} se puede utilizar para encontrar la caída de voltaje a través de una resistencia si conocemos la corriente a través de ella. Por último, podemos usar la última versión si necesitamos establecer la corriente a un cierto valor y tenemos que encontrar la resistencia requerida para hacerlo.
Se utiliza una batería de 9 voltios en serie para alimentar una\( \Omega \) resistencia de 40 como se muestra en la Figura 3.5.2 . Determinar la corriente circulante. También determine la potencia nominal mínima para la resistencia.
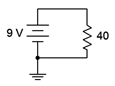
Figura 3.5.2 : Circuito por ejemplo 3.5.1 .
\[I = \frac{V}{R} \nonumber \]
\[I = \frac{9 V}{40 \Omega} \nonumber \]
\[I = 0.225amps \nonumber \]
De la ley del poder, Ecuación 2.5.3,
\[P = I \times V \nonumber \]
\[P = 0.225 A \times 9 V \nonumber \]
\[P = 2.025 watts \nonumber \]
La potencia también se podría determinar usando\(V^2 /R\) o\(I^2R\). Pruébalo. Deberías obtener el mismo resultado.
Simulación por Computadora
Para verificar los resultados del ejemplo anterior, el circuito se ingresa a un simulador, como se muestra en la Figura 3.5.3 . Aquí se usa Multisim™, aunque cualquier simulador de circuito de calidad servirá. Se utilizan DMM virtuales para medir la corriente y el voltaje. Recuerde, la corriente es la velocidad del flujo de carga y se mide en un solo punto; la mitad de un cable de conexión si se quiere. En consecuencia, el amperímetro se inserta entre la batería y la resistencia. En contraste, el voltaje es una diferencia de potencial que implica dos puntos para la medición, y así, el voltímetro se coloca a través de la resistencia.
Tenga en cuenta que el voltaje es exactamente de 9 voltios como se esperaba. La corriente es apenas tímida de los 225 miliamperios esperados. Esto se debe a que todos los amperímetros del mundo real exhiben alguna resistencia interna finita. Esta resistencia extra, aunque mucho más pequeña que la resistencia, se suma a la resistencia total y por lo tanto disminuye ligeramente la corriente. El simulador ha sido programado para imitar este comportamiento y así vemos una disminución muy leve en la corriente en la simulación, que es precisamente el efecto que veríamos en un laboratorio físico adecuado.
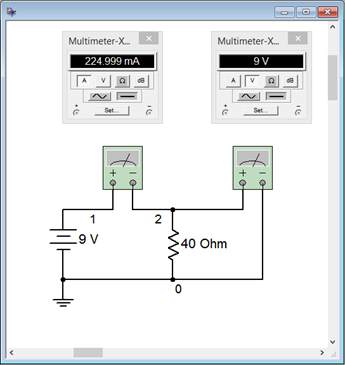
Figura 3.5.3 : El circuito de Ejemplo 3.5.1 en un simulador.
Esta simulación utiliza instrumentos virtuales porque hacen eco de la disposición de un laboratorio físico y ofrecen cierta familiaridad. Desafortunadamente, se vuelven engorrosos en circuitos más grandes. Analizaremos otras técnicas de simulación, más directas, más adelante en este capítulo.
Consulte el circuito de la batería y la lámpara que se muestra en la Figura 3.3.1. Determinar la resistencia de la lámpara si la corriente que fluye a través de ella es de 300 mA y el voltaje de la batería es de 6 voltios. Determinar también la potencia disipada por la lámpara.
\[R = \frac{V}{I} \nonumber \]
\[R = \frac{6 V}{0.3A} \nonumber \]
\[R = 20 \Omega \nonumber \]
De la ley del poder,
\[P = I^2 \times R \nonumber \]
\[P = 0.3A^2 \times 20 \Omega \nonumber \]
\[P = 1.8 watts \nonumber \]
Continuemos con un par de ejemplos utilizando fuentes actuales.
Determine el voltaje desarrollado a través de la resistencia en el circuito de la Figura 3.5.4 . Determinar también la potencia disipada.
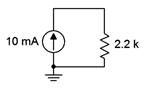
Figura 3.5.4 : Circuito para Ejemplo 3.5.3 .
\[V = I \times R \nonumber \]
\[V = 10 mA \times 2.2k \Omega \nonumber \]
\[V =22 volts \nonumber \]
De la ley del poder,
\[P = I^2 \times R \nonumber \]
\[P = (10 mA)^2 \times 2.2 k \Omega \nonumber \]
\[P = 0.22 watts \nonumber \]
Pista computacional: no olvides la parte “milli” de la corriente (milli al cuadrado es micro).
Determine el valor de resistencia requerido en el circuito de la Figura 3.5.5 para que la fuente genere 24 watts de potencia.
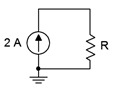
Figura 3.5.5 : Circuito para Ejemplo 3.5.4 .
Primero, tenga en cuenta que la energía generada debe ser igual a la potencia disipada. Así, la potencia generada por la fuente debe ser igual a la potencia disipada por la resistencia. De la ley del poder,
\[P = I^2 \times R \nonumber \]
\[R = \frac{P}{I^2} \nonumber \]
\[R = \frac{24 W}{(2 A)^2} \nonumber \]
\[R = 6 \Omega \nonumber \]
Como comprobación cruzada, tenga en cuenta que la ley de Ohm indica que una\( \Omega \) resistencia de 6 produciría una caída de 12 voltios dada una corriente de 2 amperios, y que 12 voltios por 2 amperios produce los 24 vatios esperados.
Ahora es el momento de pasar a circuitos en serie utilizando múltiples resistencias y/o fuentes de corriente.


