3.4: Combinación de componentes de la serie
- Page ID
- 85992
Por lo general, una conexión en serie incluirá múltiples resistencias. Refiriéndose de nuevo a la ecuación de resistencia presentada en el Capítulo 2, Ecuación 2.7.2, podemos ver que las resistencias en serie suman.
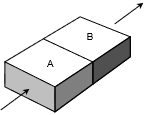
Figura 3.4.1 : Resistencias en serie.
\[R = \frac{\rho l}{A} \nonumber \]
Si consideramos dos resistencias idénticas colocadas en serie, una tras otra como en la Figura 3.4.1 , la longitud efectiva se duplicaría manteniendo la resistividad y el área sin cambios. El resultado combinado sería una duplicación de la resistencia de sólo una de ellas. Si entonces generalizamos esto a dos resistencias arbitrarias de resistividad y área idénticas, las longitudes dictarían la resistencia de cada una, y las longitudes combinadas reflejarían entonces la resistencia del par. Podemos generalizar esto aún más para\(N\) las resistencias. Así encontramos que la resistencia equivalente de un grupo de resistencias en serie es su suma:
\[R_{Total} = R_1+R_2+R_3+\dots +R_N \label{3.2} \]
En consecuencia, a medida que se suman las resistencias en serie, se puede encontrar resistencia total sumando las resistencias individuales.
Una cadena de resistencias se coloca en serie como se muestra en la Figura 3.4.2 . Sus valores son: 120\(\Omega \), 390\(\Omega \), 560\(\Omega \) y 470\(\Omega \). Determinar el valor equivalente de la serie.
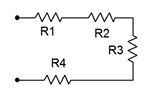
Figura 3.4.2 : Cadena de resistencia para Ejemplo 3.4.1 .
\[R_T = R_1+R_2+R_3+R_4 \nonumber \]
\[R_T = 120 \Omega +390 \Omega +560\Omega +470\Omega \nonumber \]
\[R_T =1540\Omega \nonumber \]
También se pueden agregar múltiples fuentes de voltaje en serie, sin embargo, las polaridades deben considerarse ya que los voltajes opuestos se cancelan parcialmente entre sí (es decir, agregando un negativo). Este concepto se presenta en el siguiente ejemplo.
Determinar el valor equivalente en serie de las fuentes de voltaje presentadas en la Figura 3.4.3 .
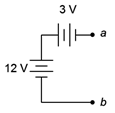
Figura 3.4.3 : Fuentes de voltaje en serie.
Si usamos el punto\(b\) como nuestra referencia, por inspección la parte superior de la fuente de 12 voltios está 12 voltios por encima del punto\(b\) (recordatorio, la barra larga denota el terminal positivo). Además, por inspección, el lado derecho de la fuente de 3 voltios (punto\(a\)) es negativo con respecto a su lado izquierdo. Como el lado izquierdo de esta fuente está conectado al terminal positivo de la fuente de 12 voltios, entonces también debe estar 12 voltios por encima del punto\(b\). Como su lado derecho es 3 voltios menos que este lado, el punto\(a\) debe ser de 3 voltios menos de 12 voltios, o 9 voltios por encima del punto\(b\). Así\(V_{ab}\) = 9 voltios.
Persiguiendo esto más, si la fuente de 3 voltios había sido volteada para que tuviera la misma polaridad que la fuente de 12 voltios (positiva hacia la derecha) entonces\(V_{ab}\) = 15 voltios. Si la fuente de 12 voltios había sido volteada (positiva hacia abajo) con la fuente de 3 voltios como se dibujó originalmente, entonces\(V_{ab}\) = −15 voltios. Si ambas fuentes habían sido volteadas entonces\(V_{ab}\) = −9 voltios. Por último, si se\(a\) hubiera tomado como referencia el punto entonces estos cuatro potenciales tendrían la polaridad opuesta porque, por definición,\(V_{ba} = −V_{ab}\).
A diferencia de las fuentes de voltaje, las diferentes fuentes de corriente no se colocan en serie ya que cada una intentaría establecer una corriente en serie diferente, una imposibilidad práctica. ¡Consulte la Figura 3.4.4 como recordatorio!
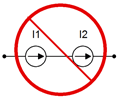
Figura 3.4.4 : Colocar fuentes actuales en serie generalmente es malo.


