3.7: Análisis en Serie

La ley de Ohm, la ley de voltaje de Kirchhoff, la regla del divisor de voltaje y las combinaciones de componentes en serie son las herramientas que usaremos para resolver problemas generales de circuitos en serie. Existen múltiples técnicas para analizar estos circuitos:

• Si se dan todos los valores de fuente de voltaje y resistencia, la corriente circulante se puede encontrar dividiendo el voltaje equivalente por la suma de las resistencias. Una vez que se encuentra la corriente, la ley de Ohm se puede utilizar para encontrar las caídas de voltaje a través de resistencias individuales. Como alternativa, las caídas de voltaje individuales se pueden encontrar usando la regla del divisor de voltaje. En ese punto, la ley de potencia se puede utilizar para encontrar la disipación de potencia en cada resistor o la potencia desarrollada por la (s) fuente (es).
• Si el circuito usa una fuente de corriente en lugar de una fuente de voltaje, entonces se conoce la corriente circulante y la caída de voltaje a través de cualquier resistencia se puede determinar directamente usando la ley de Ohm.
• Si el problema se refiere a determinar los valores de resistencia, la idea básica será utilizar estas reglas a la inversa. Por ejemplo, si se necesita un valor de resistencia para establecer una corriente específica, la resistencia total requerida se puede determinar a partir de esta corriente y el suministro de voltaje dado. Los valores de las otras resistencias en serie pueden restarse del total, produciendo el valor de resistencia requerido. Del mismo modo, si se conocen los voltajes a través de dos resistencias, siempre y cuando se conozca uno de los valores de resistencia, la otra resistencia se puede determinar usando la regla del divisor de voltaje o la ley de Ohm.

A menudo, habrá más de una manera de resolver un problema dado. Nos referiremos a estos como caminos de solución. Ningún camino en particular es “más correcto” que cualquier otro, aunque algunos caminos pueden ser más cortos o más fáciles en un caso dado, como se ilustrará a continuación.

Ejemplo 3.7.1

Determine el voltaje\(V_b\) (es decir, el voltaje a través de la\(\Omega \) resistencia 100) en el circuito de la Figura 3.7.1 . Determinar también la corriente circulante.

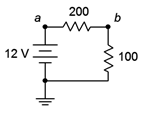
Figura 3.7.1 : Circuito por ejemplo 3.7.1 .

Primero, tenga en cuenta que hay una sola fuente de voltaje que creará una corriente en sentido horario que fluye a través de las dos resistencias. KVL dice que las caídas combinadas a través de esas resistencias deben ser iguales a la subida de la fuente, o 12 voltios. Una ruta de solución implica primero encontrar la resistencia total. Dividir esto en el voltaje de la fuente generará la corriente. La ley de Ohm se puede usar para determinar el voltaje de la resistencia.

\[R_T = R_1+R_2 \nonumber \]

\[R_T = 200 \Omega +100 \Omega \nonumber \]

\[R_T = 300 \Omega \nonumber \]

\[I = \frac{E}{R_T} \nonumber \]

\[I = \frac{12 V}{300\Omega} \nonumber \]

\[I = 40 mA \nonumber \]

\[V_b = I \times R_2 \nonumber \]

\[V_b = 40 mA \times 100\Omega \nonumber \]

\[V_b = 4 \text{ volts} \nonumber \]

Una segunda ruta de solución implica primero encontrar el voltaje de la resistencia a través de la regla del divisor de voltaje. La corriente se puede encontrar entonces a través de la ley de Ohm.

\[V_b = E \frac{R_2}{R_T} \nonumber \]

\[V_b = 12V \frac{100 \Omega}{300\Omega} \nonumber \]

\[V_b = 4 \text{ volts} \nonumber \]

\[I = \frac{V_b}{R_2} \nonumber \]

\[I = \frac{4V}{100 \Omega} \nonumber \]

\[I = 40 mA \nonumber \]

Simulación por Computadora

Verifiquemos el ejemplo anterior usando una simulación por computadora. En lugar de usar instrumentos virtuales, utilizaremos una ruta más directa, es decir, una lista de voltajes de nodo. Un voltaje de nodo es el voltaje en un punto dado con respecto a algún otro punto, normalmente a tierra, como\(V_b\) en el ejemplo anterior. Tenga en cuenta que como tratamos los cables de conexión de manera ideal (sin resistencia), un nodo es todo el cable de conexión, no una ubicación específica en él. Normalmente, los simuladores numerarán automáticamente cada nodo en un circuito con tierra siendo el nodo 0. Este método omite todo el negocio de insertar medidores virtuales en el circuito y reduce el desorden esquemático.

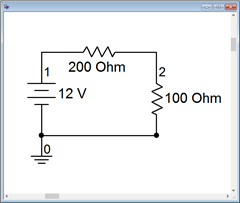
Figura 3.7.2 : El circuito del Ejemplo 3.7.1 en el simulador.

Obsérvese que la tierra es el nodo 0, la conexión de la fuente de alimentación a la primera resistencia es el nodo 1 y la conexión entre las dos resistencias es el nodo 2. Así, el nodo 2 es\(V_b\). Se realiza un análisis de punto de funcionamiento de CC. Los resultados se muestran en una ventana de salida separada, como se muestra en la Figura 3.7.3 . Los valores son los esperados y sin efectos de carga como podría verse con los instrumentos virtuales.

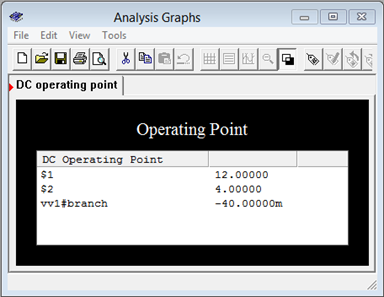
Figura 3.7.3 : Resultados de simulación para el circuito de la Figura 3.7.2 .

Ejemplo 3.7.2

Determine el voltaje\(V_a\) (es decir, el voltaje a través de la fuente de corriente) en el circuito de la Figura 3.7.4 .

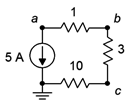
Figura 3.7.4 : Circuito para Ejemplo 3.7.2 .

Dada la dirección de la fuente de corriente, la corriente fluirá en sentido antihorario. Esto produce caídas de voltaje (más a menos) de izquierda a derecha a través de la 10\(\Omega \), de abajo a arriba a través de la 3\(\Omega \), y de derecha a izquierda a través de la\(\Omega \) resistencia 1. Esto significa que el nodo\(a\) es negativo con respecto a tierra (es decir, el voltaje sigue cayendo a través de las resistencias a medida que viajamos en sentido antihorario desde tierra, lo que indica que el potencial resultante sigue volviéndose cada vez más negativo con respecto a tierra). Para encontrar\(V_a\), podemos simplemente sumar las resistencias y luego usar la ley de Ohm para determinar su caída de voltaje combinada, que por supuesto, debe igualar el aumento de voltaje de la fuente de corriente.

\[R_T = R_1+R_2+R_3 \nonumber \]

\[R_T = 1\Omega +3\Omega +10\Omega \nonumber \]

\[R_T = 14\Omega \nonumber \]

\[V_a = −I \times R_T \nonumber \]

\[V_a = −5 A \times 14 \Omega \nonumber \]

\[V_a = −70 \text{ volts} \nonumber \]

Un punto práctico al diseñar circuitos es apreciar las variaciones de corriente y voltaje producidas por las tolerancias de los componentes. Por ejemplo, en el problema anterior, determinamos que habrá 70 voltios a través de la fuente de corriente, pero esto supone que los valores de la resistencia son exactamente como se indica. En el capítulo anterior descubrimos que todos los valores de resistencia variarán algo, y calificamos esta variación como porcentaje de tolerancia. Por lo tanto, si los valores verdaderos de la resistencia están un poco apagados, esperaríamos que esto impacte en los voltajes asociados. A menudo, nos gustaría determinar valores en el peor de los casos, como un voltaje máximo o una corriente mínima. En ocasiones estas condiciones ocurren cuando todas las resistencias están en su valor máximo o mínimo. Por ejemplo, el valor máximo de voltaje de fuente en el problema anterior ocurre cuando todos los valores de resistencia están en su máximo. Sin embargo, no siempre es así. A veces los mínimos y máximos se logran con combinaciones impares, como una resistencia que está al máximo y otra al mínimo. Por ejemplo, en el circuito utilizado para el Ejemplo 3.7.1 ,\(V_b\) estará al mínimo cuando\(R_2\) esté al mínimo y cuando\(R_1\) esté en el máximo. Esto se puede verificar fácilmente usando VDR.

Simulación por Computadora

Junto con el peor de los casos, también nos gustaría saber el tipo de propagación típica que obtenemos en un parámetro particular usando variaciones de componentes normales. Esto se puede realizar en un simulador y suele llamarse Montecarlo Analysis o algo similar. Básicamente, el simulador calcula una serie de ejecuciones de simulación, cada una con valores de componentes elegidos aleatoriamente dentro de las tolerancias especificadas de los componentes elegidos, imitando el efecto de sacar los componentes de un contenedor de piezas. Para ilustrar la técnica de Montecarlo, el circuito de Ejemplo 3.7.2 se ingresa en un simulador como se muestra en la Figura 3.7.5 .

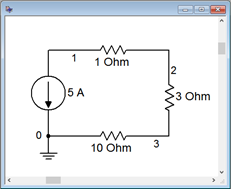
Figura 3.7.5 : El circuito del Ejemplo 3.7.2 en el simulador.

A las resistencias se les da 10% de tolerancias. Se especifican cinco corridas para el voltaje del nodo 1 que es equivalente al\(V_a\) del circuito original. Los resultados se muestran en la Figura 3.7.6 . Tenga en cuenta que el valor nominal de ejecución indica −70 voltios como se esperaba. Las otras corridas muestran variaciones en este voltaje, algunas por encima y otras por debajo del resultado nominal.

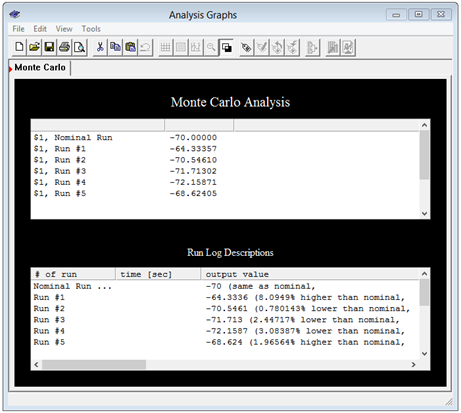
Figura 3.7.6 : Resultados de simulación para el circuito de la Figura 3.7.5 .

La importancia de la polaridad

Un elemento clave de importancia al analizar circuitos en serie, o de hecho cualquier circuito eléctrico, es anotar la polaridad de los voltajes. Esto fue evidente en el Ejemplo 3.7.2 . Determinar la polaridad para las fuentes de voltaje es fácil ya que su polaridad es fija (el positivo siempre está en la “barra larga” y negativo en la “barra corta”). La polaridad de cualquier resistencia dependerá de la dirección del flujo de corriente. Para evitar confusiones usaremos el siguiente estándar:

• Donde la corriente convencional ingresa a una resistencia, etiquetamos este punto con un signo más, y donde sale la corriente, un signo menos.
• Durante el análisis, pasar de más a menos es una caída de voltaje. Es decir, estamos pasando de un potencial más positivo o superior a un potencial menos positivo o menor, de esta manera “bajando” el voltaje.
• Del mismo modo, atravesar de menos a más es un aumento de voltaje.

Recuerde, la ley de voltaje de Kirchhoff establece que la suma de aumentos de voltaje alrededor de un bucle en serie debe ser igual a la suma de caídas de voltaje.

Además de determinar el voltaje a través de resistencias individuales, a menudo estamos interesados en determinar el voltaje entre puntos arbitrarios en un circuito. Estos pueden comprender varios componentes. Es imperativo que conozcamos las polaridades de los voltajes individuales para determinar el voltaje entre dos puntos de circuito cualesquiera. Lo anterior se ilustra usando el esquema de circuito en serie de la Figura 3.7.7 .

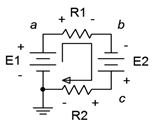
Figura 3.7.7 : Un circuito en serie multifuente y multiresistencia.

Aquí, las dos fuentes de voltaje,\(E_1\) y\(E_2\), se ayudan entre sí porque ambas están tratando de establecer una corriente en el sentido de las agujas del reloj. Esto produce un voltaje neto de\(E_1+E_2\). Sus polaridades son fijas. La dirección de la corriente será como se dibuja porque la corriente convencional fluye fuera del terminal positivo de una fuente de voltaje. El valor de esta corriente será\((E_1+E_2) / (R_1+R_2)\) a través de la ley de Ohm. Conociendo la dirección de la corriente, se pueden encontrar las polaridades de las caídas de voltaje a través de las dos resistencias. El punto donde la corriente ingresa a la resistencia es positivo, y negativo donde sale. Una vez que estos están etiquetados, se puede usar la ley de Ohm o la regla del divisor de voltaje para determinar los voltajes desarrollados a través de las dos resistencias. Tenga en cuenta que KVL establece que la suma de estos dos voltajes de resistencia debe ser igual a la tensión neta suministrada, o\(E_1+E_2\) en este caso.

Para determinar el voltaje de punto\(a\) a punto\(c\), o bien\(V_{ac}\), partimos en punto\(a\) y sumamos las caídas de voltaje y se eleva hasta llegar al punto\(c\). Aquí, el voltaje transversal se\(R_1\) muestra como una caída (+ a − y tomado como positivo) y el voltaje transversal se\(E_2\) muestra como un aumento (− a +, y por lo tanto negativo). El resultado es el voltaje a través\(R_1\) menos el voltaje a través\(E_2\). Dependiendo de los valores específicos, la suma puede terminar siendo un valor positivo o negativo. Si es positivo, esto significa que el punto\(a\) está en un potencial mayor que el punto\(c\). Por el contrario, si es negativo, esto significa que el punto\(a\) está en un potencial menor que el punto\(c\). Si invertimos el orden, comenzando en punto\(c\) y moviéndonos a punto\(a\), o bien\(V_{ca}\), terminaremos con la misma magnitud de voltaje pero el signo volteará. En el laboratorio, la primera letra de punto (la\(a\)\(V_{ac}\) entrada) es donde se conecta el cable rojo del voltímetro y la segunda letra es donde se conecta el cable negro. Como recordatorio, si se usa un solo punto de conexión, como en\(V_a\), se supone que la segunda letra está conectada a tierra. Así,\(V_a\) es el voltaje de punto\(a\) a tierra.

Para ilustrar la importancia de la polaridad de la fuente de voltaje, considere el circuito en serie que se muestra en la Figura 3.7.8 . Este circuito es idéntico al circuito anterior con la excepción de que se\(E_2\) ha volteado la polaridad de la fuente. Esto puede tener un cambio drástico en las caídas de corriente y voltaje resultantes. Por ejemplo, si\(E_2\) es mayor que\(E_1\), la tensión neta suministrada será\(E_2−E_1\) y la dirección de la corriente convencional será la dibujada. Efectivamente,\(E_2\) se estará cobrando\(E_1\). Tenga en cuenta que esto es opuesto al circuito anterior. Debido a que tanto la dirección como la magnitud de la corriente han cambiado, las caídas de voltaje y las polaridades de\(R_1\) y\(R_2\) cambiarán. En consecuencia, cualquier voltaje punto a punto\(V_{ac}\), como, también cambiará.

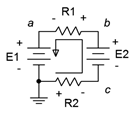
Figura 3.7.8 : Circuito en serie con polaridad alterada.

Ejemplo 3.7.3

Determinar los voltajes\(V_b\) y\(V_{ca}\) en el circuito de la Figura 3.7.9 .

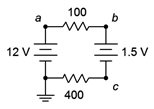
Figura 3.7.9 : Circuito para Ejemplo 3.7.3 .

El primer paso aquí sería señalar que las dos fuentes están en oposición. El resultado es una fuente efectiva de 10.5 voltios con la misma polaridad que la fuente de 12 voltios, lo que significa que crea una corriente en sentido horario (más bien lo contrario de la Figura 3.7.8 ). La resistencia total será la suma de las resistencias, o 500\(\Omega \). A partir de esto podemos calcular la corriente y luego el voltaje cae a través de cada resistor. La polaridad a través del 100\(\Omega \) será de + a − de izquierda a derecha, y a través del 400\(\Omega \) será de + a − de derecha a izquierda. Las polaridades para ambas fuentes son de arriba a abajo + a −. Esto se muestra en la Figura 3.7.10 .

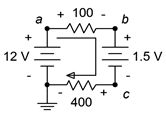
Figura 3.7.10 : Circuito por Ejemplo 3.7.3 con dirección de corriente y polaridades de voltaje mostradas.

\[I = \frac{E_{Total}}{R_{Total}} \nonumber \]

\[I = \frac{10.5 V}{500 \Omega} \nonumber \]

\[I = 21 mA \nonumber \]

\[V_{100} = I \times R_{100} \nonumber \]

\[V_{100} = 21 mA \times 100\Omega \nonumber \]

\[V_{100} = 2.1 \text{ volts} \nonumber \]

\[V_{400} = I \times R_{400} \nonumber \]

\[V_{400} = 21 mA \times 400\Omega \nonumber \]

\[V_{400} = 8.4 \text{ volts} \nonumber \]

Para encontrar\(V_b\) comenzamos en nodo\(b\) y trabajamos nuestro camino a tierra, sumando los potenciales a medida que avanzamos. Primero vemos la fuente de 1.5 voltios. A pesar de que se trata de una fuente, todavía se considera una caída de voltaje porque la polaridad es de + a −. La polaridad en la\(\Omega \) resistencia 400 es la misma, por lo que sumamos en sus 8.4 voltios para 9.9 voltios totales. Es decir, el nodo\(b\) está a 9.9 voltios sobre tierra.

Porque\(V_{ca}\) procedemos de manera similar. Comenzando en el nodo\(c\) nos movemos a través de la fuente de 1.5 voltios, pero esta vez la polaridad es − a +, o una subida de 1.5 voltios (es decir, tomada como negativa). Ahora en el nodo\(b\), continuamos a través de la\(\Omega \) resistencia 100, viendo también una polaridad − a +, o una subida de 2.1 voltios. Eso suma 3.6 voltios de magnitud, sin embargo, el nodo de arranque es menor que el nodo final, por lo tanto\(V_{ca}\) = −3.6 voltios. También podríamos decir\(V_{ac}\) = 3.6 voltios.

De vuelta en el Capítulo 2 se presentó la analogía de altura para voltaje. Esto se puede aplicar muy bien en el ejemplo anterior. Se puede pensar en el suelo como literalmente tierra: la tierra bajo tus pies. Las subidas de voltaje serían como subir una escalera y las caídas de voltaje serían como bajar una escalera. Piense en cada voltio como análogo a un pie o un metro. Así, para\(V_b\), subes por la escalera 8.4 pies para el 400\(\Omega \) y otro 1.5 pies para la fuente de 1.5 voltios, dejándote 9.9 pies (voltios) por encima del suelo. Por lo tanto,\(V_b\) debe ser positivo con respecto a tierra por 9.9 voltios. Esta analogía también funciona para voltajes bajo tierra: solo piensa en términos de cavar un agujero. Para voltajes que no se refieren al suelo, piensa en subir y bajar escaleras, y luego comparar la altura de donde te detuviste con la altura de donde empezaste.

Etiquetar con precisión cada polaridad de voltaje puede parecer un trabajo innecesario, pero a medida que aumenta la complejidad del circuito también lo hace la oportunidad de errores de polaridad. No se debe omitir este importante paso. Considera el siguiente ejemplo el cual es sólo un poco más complejo que el anterior.

Ejemplo 3.7.4

Determine el voltaje\(V_{be}\) en el circuito de la Figura 3.7.11 .

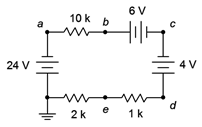
Figura 3.7.11 : Circuito para Ejemplo 3.7.4 .

Las fuentes de 24 voltios y 6 voltios se están ayudando entre sí mientras que la fuente de 4 voltios está en oposición. El resultado es un potencial efectivo suministrado de 26 voltios con una corriente circulando en sentido antihorario. La dirección de la corriente y las polaridades de voltaje se muestran en la Figura 3.7.12 .

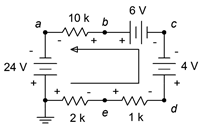
Figura 3.7.12 : Circuito por Ejemplo 3.7.4 con dirección de corriente y polaridades de voltaje mostradas.

Primero, encuentre la corriente circulante y luego encuentre las caídas de voltaje a través de las resistencias de interés. La resistencia total es la suma de los tres, o 13 k\(\Omega \).

\[I = \frac{E_{Total}}{R_{Total}} \nonumber \]

\[I = \frac{26 V}{13 k \Omega} \nonumber \]

\[I = 2 mA \nonumber \]

\[V_{10k} = I \times R_1 \nonumber \]

\[V_{10k} = 2 mA \times 10 k \Omega \nonumber \]

\[V_{10k} = 20 \text{ volts} \nonumber \]

De igual manera,\(V_{2k}\) = 4 voltios y\(V_{1k}\) = 2 voltios con las polaridades mostradas. Para determinar\(V_{be}\), podemos comenzar en nodo\(b\) y movernos a nodo ya sea\(e\) yendo al lado izquierdo o derecho. Haremos ambas cosas y compararemos los resultados.

Yendo hacia la izquierda, vemos + a − 20 voltios a través de los 10 k\(\Omega \), − a + 24 a través de la fuente del lado izquierdo, y luego + a − 4 voltios a través de los 2 k\(\Omega \). Esto suma 0 voltios, lo que significa que los nodos\(b\) y\(e\) están al mismo potencial! Doble comprobación bajando por el lado derecho vemos + a − 6 voltios para la fuente superior, − a + 4 voltios para la fuente del lado derecho, y finalmente − a + 2 voltios para el 1 k\(\Omega \). Esto también es de 0 voltios, como se esperaba.

Es importante entender que decir\(V_{be}\) = 0 voltios no implica eso\(V_b\) o\(V_e\) son 0 voltios. De hecho, podemos ver que\(V_e\) está bajo tierra por el voltaje caído a través de los 2 k\(\Omega \), o −4 voltios. Del mismo modo,\(V_b\) está por encima del nodo\(a\) por 20 voltios, y el nodo\(a\) en sí está 24 voltios por debajo de tierra dada la polaridad de la fuente del lado izquierdo. El resultado, una vez más, es de −4 voltios.

Un ejemplo más para ilustrar mejor la regla del divisor de voltaje en un circuito más grande.

Ejemplo 3.7.5

Determine los voltajes\(V_b\),,\(V_d\), y\(V_{bd}\) en el circuito de la Figura 3.7.13 .

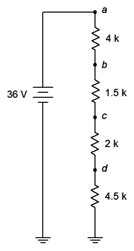
Figura 3.7.13 : Circuito por ejemplo 3.7.5 .

Si bien podríamos encontrar la corriente circulante, luego usar la ley de Ohm para encontrar las caídas de voltaje individuales, y finalmente agregar estas piezas para encontrar los potenciales que estamos buscando, en cambio, nos enfocaremos en usar VDR que puede ser más rápido.

La regla del divisor de voltaje establece que el voltaje a través de cualquier resistencia o grupo de resistencias en un bucle en serie es proporcional a su resistencia en comparación con la resistencia total en ese bucle. La resistencia total en este circuito es de 12 k\(\Omega \). Para encontrar el voltaje a través de cualquier resistencia o grupo de resistencias, simplemente hacemos una relación de la resistencia de interés a la resistencia total y multiplicamos por la tensión de fuente aplicada. Numeración de las resistencias R\(_1\) en la parte superior a R\(_4\) en la parte inferior:

\[V_d = E \frac{R_4}{R_T} \nonumber \]

\[V_d = 36 V \frac{4.5 k\Omega}{12 k\Omega} \nonumber \]

\[V_d = 13.5 \text{ volts} \nonumber \]

\[V_b = E \frac{R_2+R_3+R_4}{R_T} \nonumber \]

\[V_b = 36V \frac{8k \Omega}{12 k \Omega} \nonumber \]

\[V_b = 24 \text{ volts} \nonumber \]

\[V_{bd} = E \frac{R_2+R_3}{R_T} \nonumber \]

\[V_{bd} = 36 V \frac{3.5 k \Omega}{12 k\Omega} \nonumber \]

\[V_{bd} = 10.5 \text{ volts} \nonumber \]

Hay otra manera de encontrar\(V_{bd}\) aquí, y es notar eso por definición\(V_{bd} = V_b − V_d\). Por lo tanto,\(V_{bd}\) = 24 voltios − 13.5 voltios, o 10.5 voltios.