3.8: Potenciómetros y Reóstatos

Algunas aplicaciones requieren el uso de resistencias variables. Un ejemplo es un control de volumen básico, pero otros ejemplos incluyen la calibración del equipo y parámetros ajustables por el usuario como los controles de graves, agudos y equilibrio en un sistema de audio doméstico. Las resistencias ajustables se encuentran en dos categorías, potenciómetros y reóstatos. Generalmente, estos serían el mismo dispositivo físico, con la aplicación y el uso determinando su nombre.

Un potenciómetro es una resistencia con tres conductores. Junto con los cables finales típicos, hay un tercer cable denominado limpiaparabrisas o grifo. Este tercer cable está conectado a un pequeño brazo metálico que hace contacto con el material resistivo y que puede moverse a lo largo de la longitud del material. Los potenciómetros, o macetas para abreviar, a menudo se forman en forma circular (recorrido giratorio) pero también pueden ser en forma de línea recta (recorrido lineal). Varios tipos diferentes se muestran en la Figura 3.8.1 . Las unidades circulares más grandes con ejes y la unidad recta en la parte superior están diseñadas para ser ajustadas por el usuario final (las perillas apropiadamente elegantes están unidas a dichos ejes, por supuesto), mientras que las unidades más pequeñas están diseñadas para ser ajustadas solo por un técnico (tenga en cuenta las pequeñas ranuras de tornillo de ajuste destinadas a recibir destornilladores finos). Las unidades más pequeñas están diseñadas para montarse directamente en una placa de circuito impreso, mientras que las unidades ajustables por el usuario están montadas en un panel frontal y tienen orejetas de cableado en lugar de cables rectos.

Figura 3.8.1 : Una variedad de potenciómetros.

En la Figura 3.8.2 se muestra una vista en corte de una olla de montaje en panel giratorio con su carcasa trasera retirada.

Figura 3.8.2 : Vista en corte de un potenciómetro rotativo.

La mayoría de los potenciómetros circulares utilizan una\(^{\circ}\) rotación de 270 de extremo a extremo, también conocida como “3/4 de vuelta”. Algunos recipientes de precisión utilizados para la calibración pueden usar un engranaje helicoidal interno para mover el limpiaparabrisas y lograr 20 o más vueltas para trasladar el limpiaparabrisas de un extremo al otro. Esto da como resultado la capacidad de hacer ajustes muy finos. Las unidades rectangulares en el centro derecho de la Figura 3.8.1 son ejemplos de este tipo.

El símbolo esquemático de un potenciómetro básico se muestra en la Figura 3.8.3 . Para mayor comodidad, sus terminales están etiquetados A y B para los dos extremos y W para el brazo del limpiaparabrisas.

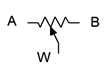
Figura 3.8.3 : Símbolo esquemático para un potenciómetro, con etiquetas.

Un bote se puede visualizar como dos resistencias en secuencia con un toque entre ellas. La resistencia total nunca cambia. Lo que sí cambia es la proporción de las dos piezas.

\[R_{AB} = R_{AW} + R_{WB} \label{3.6} \]

En el extremo izquierdo de recorrido,\(R_{AW}\) será 0 y\(R_{WB}\) será igual a\(R_{AB}\). En la extrema derecha,\(R_{AW}\) igualará\(R_{AB}\) y\(R_{WB}\) será 0. Si el limpiaparabrisas está precisamente en el medio, entonces\(R_{AW} = R_{WB} = R_{AB}/2\), y así sucesivamente ¹.

Como resultado, los potenciómetros son muy útiles como divisores de voltaje controlables (de ahí el nombre). A veces es deseable controlar dos señales simultáneamente desde una sola perilla (por ejemplo, una perilla de volumen para un estéreo de alta fidelidad controla tanto los canales izquierdo como el derecho). Para esta aplicación, se pueden apilar múltiples elementos resistivos y utilizar un eje común para controlar todos los brazos del limpiaparabrisas en tándem. Estos se conocen como potenciómetros agrupados. La unidad alta y redonda en el centro izquierdo de la Figura 3.8.1 es una olla de doble banda. Tenga en cuenta que tiene un total de seis orejetas de soldadura, tres para el elemento superior y tres para el elemento posterior. Finalmente, a diferencia de las resistencias fijas, las macetas están disponibles en tamaños limitados. Los valores típicos utilizan múltiplos de 1 o 5 para la resistencia total (por ejemplo\( \Omega \), 1 k, 5 k\( \Omega \), 10 k\( \Omega \), etc.) aunque también se dispone de una selección limitada de otros tamaños.

Si solo se usa el limpiaparabrisas y solo uno de los dos terminales terminales, entonces el dispositivo se conoce como reóstato. Los reóstatos se utilizan a menudo para limitar la corriente. El valor del reóstato oscila entre 0 y el valor nominal del potenciómetro. Los símbolos esquemáticos para un reóstato se muestran en la Figura 3.8.4 . El símbolo ANSI se muestra a la izquierda y la versión IEC a la derecha.

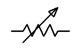
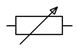
Figura 3.8.4 : Símbolos esquemáticos para un reóstato: ANSI (derecha) e IEC (izquierda).

Tiempo para un par de ejemplos.

Ejemplo 3.8.1

Para el circuito representado en la Figura 3.8.5 , determinar los voltajes máximo y mínimo para\(V_c\), así como su valor cuando el pote se ajusta a mitad de camino (asumir conicidad lineal).

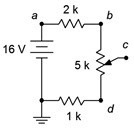
Figura 3.8.5 : Circuito por ejemplo 3.8.1 .

La regla del divisor de voltaje establece que el voltaje a través de cualquier resistencia o grupo de resistencias en un bucle en serie es proporcional a su resistencia en comparación con la resistencia total en ese bucle. La resistencia total en este circuito es de 8 k\( \Omega \). El voltaje en el nodo\(c\) dependerá de la configuración de la olla. El voltaje máximo se produce cuando el limpiaparabrisas está todo el camino hacia arriba, contactando con el nodo\(b\).

\[V_c (max) = E \frac{R_i}{R_T} \nonumber \]

\[V_c (max ) = 16 V \frac{6 k \Omega}{ 8 k \Omega} \nonumber \]

\[V_c (max ) = 12 \text{ volts} \nonumber \]

Para el caso mínimo, el limpiaparabrisas está ajustado completamente hacia abajo, contactando con el nodo\(d\).

\[V_c (min) = E \frac{R_i}{R_T} \nonumber \]

\[V_c (min) = 16V \frac{1 k \Omega}{ 8 k \Omega} \nonumber \]

\[V_c (min) = 2 \text{ volts} \nonumber \]

Para el caso a mitad de camino, la olla puede tratarse como dos\( \Omega \) resistencias de 2.5 k.

\[V_c (mid ) = E \frac{R_i}{R_T} \nonumber \]

\[V_c (mid ) = 16 V \frac{3.5k \Omega}{ 8 k \Omega} \nonumber \]

\[V_c (mid ) = 7 \text{ volts} \nonumber \]

Tenga en cuenta que la posición media logra un voltaje a medio camino entre los extremos.

De esta manera la olla permite un rango de ajuste de voltaje entre un mínimo de 2 voltios y un máximo de 12 voltios. Las resistencias fijas superior e inferior sirven para establecer estos límites. Cuanto mayores sean los valores de estas resistencias en comparación con el valor del bote, más estrecho será el rango de ajuste. Si se excluyeran estas dos resistencias, la olla permitiría todo el rango de ajuste, desde tierra (0 voltios) hasta el valor de la fuente de alimentación de 16 voltios.

Ejemplo 3.8.2

El potenciómetro en el circuito de la Figura 3.8.6 está conectado como un reóstato. Determinar la corriente máxima y mínima en el circuito.

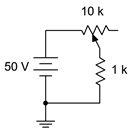
Figura 3.8.6 : Circuito por ejemplo 3.8.2 .

El reóstato presentará un valor de resistencia entre 0\( \Omega \) y 10 k\( \Omega \). El caso de corriente máxima ocurre cuando el limpiaparabrisas se establece en el extremo izquierdo, produciendo 0\( \Omega \).

\[I (max) = \frac{E}{R_T} \nonumber \]

\[I (max) = \frac{50 V}{1 k \Omega} \nonumber \]

\[I (max) = 50 mA \nonumber \]

Para el caso mínimo, el limpiaparabrisas se coloca todo el camino hacia la derecha, produciendo los 10 k completos\( \Omega \).

\[I (min) = \frac{E}{R_T} \nonumber \]

\[I (min) = \frac{50 V}{11 k \Omega} \nonumber \]

\[I (min) = 4.545 mA \nonumber \]

Referencias

¹ Esta división 50/50 es verdadera si el bote tiene un ahusamiento lineal, lo que significa que el cambio de resistencia es proporcional a la posición del limpiaparabrisas. Si bien esto es típico, es posible tener un cono que no sea lineal para aplicaciones especiales, como el cono de audio. En estos dispositivos la relación de resistencia en la posición media podría ser algo así como 10/90 en lugar de 50/50. Esto sería deseable para un control de volumen porque el oído humano responde a los cambios en la presión sonora de manera logarítmica. El uso de una olla cónica lineal daría como resultado un control de volumen que es demasiado sensible en un extremo y, sin embargo, apenas produce ningún cambio en el otro extremo.