5.4: Análisis Serie-Paralelo

El análisis de redes serie-paralelo implica reconocer aquellos subcircuitos que están en serie o que están en paralelo entre ellos, realizar simplificaciones según sea necesario y enrollar con un equivalente simple solo en serie o solo paralelo. Entonces las diversas leyes como la ley de Ohm, KVL, KCL, VDR y CDR se aplican a las diversas redes simplificadas para determinar los parámetros de interés. No existe una única técnica de solución, cada circuito es único.

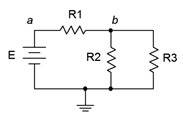
Figura 5.4.1 : Un simple circuito serie-paralelo.

Comencemos considerando el circuito de la Figura 5.4.1 . Para revisar, esto no es solo un circuito en serie ni solo un circuito paralelo. Si se tratara de un circuito en serie entonces la corriente a través de todos los componentes tendría que ser la misma, es decir, no habría nodos donde la corriente pudiera dividirse. Esto claramente no es el caso ya que la corriente que fluye a través\(R_1\) puede dividirse en el nodo\(b\), con una porción fluyendo hacia abajo\(R_2\) y el resto a través\(R_3\). Por otro lado, si fuera estrictamente paralelo, entonces todos los componentes tendrían que exhibir la misma tensión y por lo tanto solo habría dos puntos de conexión en el circuito. Este tampoco es el caso ya que hay tres puntos de este tipo:\(a\),\(b\) y suelo.

Lo que es cierto es que las resistencias\(R_2\) y\(R_3\) están en paralelo. Esto lo sabemos porque ambos componentes están unidos a los mismos dos nodos,\(b\) y tierra, y deben exhibir el mismo voltaje,\(V_b\). Como tal, podemos encontrar la resistencia equivalente de este par y tratar el resultado como una sola resistencia, llamémoslo\(R_x\). En este circuito recién simplificado, Rx está en serie con\(R_1\) y la fuente,\(E\). Hemos reducido el circuito original a un circuito en serie simple y, por lo tanto, se pueden aplicar las reglas de análisis en serie.

Hay muchas vías de solución en este punto. Por ejemplo, podríamos encontrar la resistencia total,\(R_t\), sumando\(R_1\) a\(R_x\). Dividiendo esto por\(E\) arroja la corriente total que fluye fuera de la fuente,\(I_{total}\). Esta corriente debe fluir a través de\(R_1\) lo que la ley de Ohm se puede utilizar para encontrar la caída de voltaje a través\(R_1\). Esta misma corriente debe estar fluyendo a través\(R_x\), por lo que la ley de Ohm se puede utilizar para encontrar el voltaje asociado (\(V_b\)). Las corrientes a través\(R_2\) y luego se\(R_3\) pueden encontrar usando la ley de Ohm para cada resistencia (por ejemplo, la corriente pasante\(R_2\) debe ser\(V_b/R_2\)). Como alternativa, estas corrientes se pueden encontrar usando la regla del divisor de corriente entre\(R_2\) y\(R_3\) (por ejemplo, la corriente pasante\(R_2\) debe ser\(I_{total} \cdot R_1/(R_1 + R_2)\); recuerde, la regla del divisor de corriente usa la relación de la resistencia opuesta sobre la suma).

Otra ruta de solución sería aplicar la regla del divisor de voltaje a\(R_1\) y con el\(R_x\) fin de derivar las dos caídas de voltaje (o la regla se puede aplicar para encontrar solo una de las caídas y la otra tensión se puede encontrar restando eso de la fuente, una aplicación de KVL). Una vez que se determinan los voltajes, se puede utilizar la ley de Ohm para encontrar las corrientes. Si se necesitan potencias, se determinan fácilmente una vez que se encuentran los voltajes y corrientes.

Ejemplo 5.4.1

Un circuito serie-paralelo se muestra en la Figura 5.4.2 . Determinar\(V_b\).

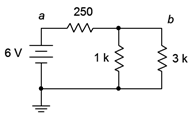
Figura 5.4.2 : Circuito por ejemplo 5.4.1 .

Como solo nos interesa encontrar una tensión, la regla del divisor de voltaje es una buena candidata. El 1 k\( \Omega \) está en paralelo con el 3 k\( \Omega \), produciendo una resistencia equivalente de 750\( \Omega \). Desde aquí aplicamos VDR.

\[V_b = E \frac{R_{eq}}{R_1+R_{eq}} \nonumber \]

\[V_b = 6V \frac{750 \Omega}{250 \Omega +750 \Omega} \nonumber \]

\[V_b = 4.5V \nonumber \]

Para aclarar las direcciones de corriente y las polaridades de voltaje, el circuito se redibuja y se etiqueta apropiadamente en la Figura 5.4.3 . Podemos verificar la respuesta de varias maneras. Por ejemplo, la Figura 5.4.3 indica, vía KVL, que la caída de voltaje a través de la\( \Omega \) resistencia 250 más\(V_b\) debe ser igual a la tensión de fuente de 6 voltios. En consecuencia,\(V_{250}\) debe ser de 6 voltios menos 4.5 voltios, o 1.5 voltios. La ley de Ohm indica entonces que la corriente a través del 250\( \Omega \) debe ser de 1.5 V/250\( \Omega \), o 6 miliamperios. Con base en la equivalencia resistiva anterior, la resistencia total vista por la fuente debe ser de 250\( \Omega \) en serie con 750\( \Omega \), o 1 k\( \Omega \). Esto indica que la corriente de la fuente debe ser de 6 V/1 k\( \Omega \), o 6 miliamperios. Como la fuente y los 250\( \Omega \) están en serie, deben ver la misma corriente. Este chequeo cruzado demuestra que lo hacen: feliz feliz alegría alegría.

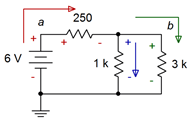
Figura 5.4.3 : Circuito por ejemplo 5.4.1 con polaridades y direcciones incluidas.

Podemos ir más allá y verificar las corrientes vía KCL. Para la primera resistencia paralela encontramos:

\[I_{1k} = \frac{V_b}{1 k \Omega} \nonumber \]

\[I_{1k} = \frac{4.5V}{1 k \Omega} \nonumber \]

\[I_{1k} = 4.5 mA \nonumber \]

Y para la segunda resistencia vemos:

\[I_{3k} = \frac{V_b}{1 k \Omega} \nonumber \]

\[I_{3k} = \frac{4.5V}{3 k \Omega} \nonumber \]

\[I_{3k} = 1.5mA \nonumber \]

Obviamente, estos suman a la corriente de entrada de 6 mA.

Ejemplo 5.4.2

Determine\(V_b\) y la corriente de origen en el circuito de la Figura 5.4.4 .

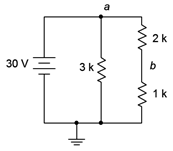
Figura 5.4.4 : Circuito para Ejemplo 5.4.2 .

En este circuito la\( \Omega \) resistencia de 3 k está en paralelo con la combinación en serie de los 2 k\( \Omega \) y 1 k\( \Omega \). Esto lleva a una resistencia equivalente de 3 k\( \Omega \) en paralelo con 3 k\( \Omega \), o 1.5 k\( \Omega \). Desde aquí podemos encontrar la corriente fuente.

\[I_s = \frac{E}{R_{Total}} \nonumber \]

\[I_s = \frac{30 V}{1.5k \Omega} \nonumber \]

\[I_s = 20mA \nonumber \]

Esta corriente debe dividirse uniformemente por las dos trayectorias verticales ya que cada una presenta 3 k\( \Omega \) de resistencia (10 mA cada una logra 30 voltios para\(V_a\), que es la fuente).

La regla del divisor de voltaje es una buena opción para\(V_b\) como conocemos el voltaje aplicado.

\[V_b = E \frac{R_{eq}}{R_1+R_{eq}} \nonumber \]

\[V_b = 30 V \frac{1k \Omega}{1k \Omega +2k \Omega} \nonumber \]

\[V_b = 10 V \nonumber \]

Para mayor claridad, el circuito se redibuja y se vuelve a etiquetar con direcciones de corriente y polaridades de voltaje en la Figura 5.4.5 . Como ejercicio adicional, tratar de verificar las respuestas anteriores utilizando medios alternos, como se ilustra en el Ejercicio 5.4.

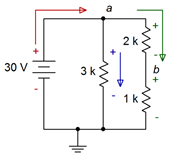
Figura 5.4.5 : Circuito por Ejemplo 5.4.2 con polaridades y direcciones incluidas.

A medida que el circuito crece, cada vez existen más rutas de solución. Considere el circuito de la Figura 5.4.6 . En este caso,\(R_3\) y\(R_4\) están en paralelo. Esta combinación paralela está en serie con\(R_2\). Finalmente, este conjunto de tres resistencias está en paralelo con\(R_1\) y\(E\), reduciéndose a un circuito paralelo. En consecuencia, sabemos que el voltaje transversal\(R_1\) debe ser igual a\(E\). También, las corrientes a través\(R_1\) y\(R_2\) deben sumar a la corriente que sale de la fuente (KCL). Además, las corrientes a través\(R_3\) y\(R_4\) deben sumarse a la corriente que fluye a través\(R_2\) (KCL). Además, los voltajes a través\(R_3\) y\(R_4\) deben ser los mismos (están en paralelo) y que este voltaje más el voltaje transversal\(R_2\) deben ser iguales\(E\) (KVL). Una ruta de solución sería encontrar la resistencia total tal como la ve la fuente\(R_1 || (R_2 + (R_3 || R_4))\), y usar esta para encontrar la corriente total que fluye fuera de la fuente. La regla de división de corriente se puede usar entonces entre\(R_1\) y la resistencia equivalente\((R_2 + (R_3 || R_4))\). La ley de Ohm se puede utilizar posteriormente para encontrar diversas caídas de voltaje. Como alternativa, la regla del divisor de voltaje se puede usar entre\(R_2\) y el equivalente paralelo\((R_3 || R_4)\) ya que esta combinación es impulsada por\(E\). Conociendo los voltajes, se pueden determinar las corrientes. Con tantas vías de solución posibles para circuitos grandes, a menudo vale la pena tomarse un momento para trazar una estrategia en lugar de simplemente “sumergirse” y esperar que todo funcione.

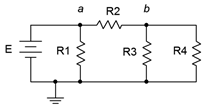
Figura 5.4.6 : Un circuito serie-paralelo un poco más complejo.

Ejemplo 5.4.3

El circuito de la Figura 5.4.7 es el mismo que la red resistiva presentada en el Ejemplo 5.3.1 pero con la adición de una fuente de voltaje. Determinar\(V_b\),\(V_c\),\(V_d\), la corriente fuente\(I_s\), y la corriente que fluye a través de la\( \Omega \) resistencia 40,\(I_{40}\).

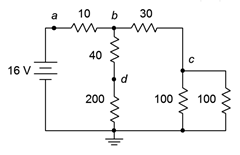
Figura 5.4.7 : Circuito para Ejemplo 5.4.3 .

Gracias al Ejemplo 5.3.1 ya se han determinado las resistencias equivalentes de varias porciones, ahorrando algo de tiempo. Para reiterar, el par de 100\( \Omega \) resistencias están en paralelo para 50\( \Omega \). Eso está en serie con el 30\( \Omega \) por 80\( \Omega \). En el camino medio, los 200\( \Omega \) y 40\( \Omega \) están en serie, produciendo 240\( \Omega \). 240\(||\) 80 = 60\( \Omega \). Esto está en serie con el 10\( \Omega \), produciendo una resistencia total cargando la fuente de 70\( \Omega \).

\[I_s = \frac{E}{R_{Total}} \nonumber \]

\[I_s = \frac{ 16V}{70 \Omega} \nonumber \]

\[I_s \approx 228.6mA \nonumber \]

Los tres voltajes se pueden encontrar rápidamente a través de VDR ya que conocemos todas las resistencias de subcircuito asociadas.

\[V_b = E \frac{R_x}{R_x+R_y} \nonumber \]

\[V_b = 16V \frac{60 \Omega}{60 \Omega +10 \Omega} \nonumber \]

\[V_b \approx 13.71V \nonumber \]

\[V_c = V_b \frac{R_x}{R_x+R_y} \nonumber \]

\[V_c = 13.71 V \frac{50 \Omega}{50 \Omega +30 \Omega} \nonumber \]

\[V_c \approx 8.57 V \nonumber \]

\[V_d = V_b \frac{R_x}{R_x+R_y} \nonumber \]

\[V_d = 13.71V \frac{200 \Omega}{200 \Omega +40 \Omega} \nonumber \]

\[V_d \approx 11.43V \nonumber \]

Por último, la corriente a través de la\( \Omega \) resistencia 40 se puede encontrar dividiendo su voltaje por su resistencia. Su voltaje es\(V_b − V_d\). Un método más rápido es señalar que debido a que está en serie con el 240\( \Omega \), sus corrientes son las mismas.

\[I_{40} = \frac{V_b}{R_{Series}} \nonumber \]

\[I_{40} = \frac{13.71 V}{240 \Omega} \nonumber \]

\[I_{40} \approx 57.1mA \nonumber \]

Una vez más el circuito se vuelve a dibujar en la Figura 5.4.8 para ilustrar las direcciones de corriente y las polaridades de voltaje. La utilidad de esto se hará aún más evidente en el siguiente ejemplo.

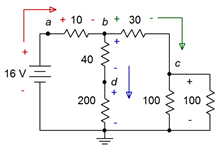
Figura 5.4.8 : Circuito por Ejemplo 5.4.3 con direcciones y polaridades.

Ejemplo 5.4.4

Determine\(V_{ac}\) y los voltajes a través de cada resistor en el circuito de la Figura 5.4.9 .

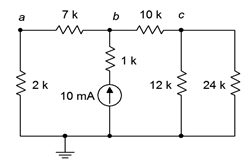
Figura 5.4.9 : Circuito para Ejemplo 5.4.3 .

Este circuito es quizás el más complejo ofrecido hasta el momento. Puede que no sea inmediatamente evidente cuáles son las polaridades de voltaje para las diversas resistencias o las direcciones de corriente adecuadas. Sin estos datos, será imposible determinar\(V_{ac}\). Para complicar las cosas, el voltaje de interés no es referenciado a tierra, sino que se refiere a dos nodos ubicados en puntos arbitrarios del circuito. Vale la pena reconocerlo, por definición\(V_{ac} = V_a − V_c\), pero ¿cómo se determinan esos voltajes?

Para ayudar con este dilema menor, el circuito ha sido redibujado en la Figura 5.4.10 . Tenga en cuenta que la fuente de corriente y la\( \Omega \) resistencia asociada de 1 k se han volteado hacia un lado, esencialmente comercializando lugares con la combinación de las\( \Omega \) series 2 k\( \Omega \) y 7 k. Esto es totalmente aceptable ya que ambos subgrupos comparten el nodo b y el suelo, lo que significa que están en paralelo. Por supuesto, el orden de los elementos paralelos en una situación como esta no importa. Esta orientación, al tener la fuente en un extremo del circuito, tiende a facilitar un poco la visualización de los flujos de corriente.

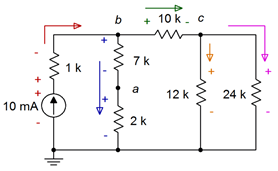
Figura 5.4.10 : Circuito por Ejemplo 5.4.3 redibujado y con polaridades y direcciones de corriente agregadas.

En cualquier caso, la corriente sale de la fuente y luego se divide en nodo\(b\), algunos se dirigen a través de los 10 k\( \Omega \) con el resto fluyendo por el combo de 7 k\( \Omega \) con la\( \Omega \) serie 2 k. En\(c\) el nodo la corriente que ingresó a los 10 k\( \Omega \) se divide nuevamente, fluyendo hacia abajo hacia el subgrupo paralelo de los 12 k\( \Omega \) y 24 k\( \Omega \). Conociendo las direcciones de corriente, las polaridades de voltaje se determinan directamente.

Ahora que el circuito ha sido redibujado, podrían venir a la mente varias rutas de solución. Para empezar, la caída de voltaje a través del 1 k\( \Omega \) es trivial ya que se conocen tanto su corriente como su resistencia. A partir de ahí, se puede utilizar un divisor de corriente para encontrar la corriente que fluye hacia abajo hacia la serie 7 k\( \Omega \) más 2 k\( \Omega \) combo. La ley de Ohm podría entonces ser utilizada para encontrar sus voltajes. Después de eso, KCL se puede utilizar para encontrar la corriente a través de los 10 k\( \Omega \) (y\(V_c\) por lo tanto su voltaje), y luego se puede aplicar la ley de Ohm para encontrar tratando las dos resistencias paralelas más a la derecha como una sola unidad.

Otra ruta de solución sería determinar la resistencia equivalente que carga la fuente de corriente. Esto permite determinar el voltaje de la fuente, después de lo cual se puede aplicar un divisor de voltaje entre el 1 k\( \Omega \) y las cinco resistencias restantes para encontrar\(V_b\). A partir de ahí, se pueden utilizar dos divisores de voltaje más para encontrar\(V_a\) y\(V_c\) que permitirán determinar los voltajes restantes de la resistencia a través de KVL. También hay otros caminos posibles pero a falta de una mejor razón, perseguiremos el primer camino que se trazó.

Antes de profundizar demasiado, sería prudente determinar las resistencias equivalentes de unos pocos subgrupos. Primero, el\( \Omega \) combo de 12 k\( \Omega \)\(||\) 24 k reduce hasta 8 k\( \Omega \). Esto está en serie con los 10 k\( \Omega \), dejando 18 k\( \Omega \) para las tres resistencias más a la derecha. En la rama media, el combo de la\( \Omega \) serie 2 k\( \Omega \) + 7 k equivale a 9 k\( \Omega \). La combinación paralela de 9 k\( \Omega \)\(||\) 18 k\( \Omega \) rinde 6 k\( \Omega \). Finalmente, este último bit está en serie con el 1 k\( \Omega \) produciendo 7 k\( \Omega \) para la resistencia equivalente de todas las resistencias.

El voltaje de la fuente y el voltaje a través de la\( \Omega \) resistencia de 1 k se determinan mediante la ley de Ohm:

\[V_{source} = I_{source} \times R_{equivalent} \nonumber \]

\[V_{source} = 10 mA \times 7k \Omega \nonumber \]

\[V_{source} = 70 V \nonumber \]

\[V_{1k} = I_{source} \times R \nonumber \]

\[V_{1k} = 10mA \times 1k \Omega \nonumber \]

\[V_{1k} = 10 V \nonumber \]

Como la fuente produce 70 voltios y la caída en el 1 k\( \Omega \) es de 10 voltios, entonces por KVL,\(V_b\) debe ser de 70 voltios − 10 voltios, o 60 voltios (lo que será útil para una comprobación cruzada en un momento). Usando un divisor de corriente, la fuente de 10 mA se divide entre las ramas media y derecha. Las resistencias equivalentes de esas ramas son 9 k\( \Omega \) y 18 k\( \Omega \), como se encontró anteriormente.

\[I_{middle} = I_{source} \frac{R_{right}}{R_{right}+R_{middle}} \nonumber \]

\[I_{middle} = 10 mA \frac{18k \Omega}{18 k \Omega +9k \Omega} \nonumber \]

\[I_{middle} \approx 6.667mA \nonumber \]

A través de KCL, la corriente de rama derecha debe ser de 10 mA − 6.667 mA, o aproximadamente 3.333 mA. Como comprobación cruzada, si 6.667 mA pasa por un total de 9 k\( \Omega \), eso produce una caída de voltaje de 60 voltios, exactamente como se esperaba del cálculo anterior para nodo\(b\). En este punto, se conoce la corriente a través de cada resistor (tratando el\( \Omega \) combo de 12 k\( \Omega \)\(||\) 24 k como una unidad) y por lo tanto la ley de Ohm puede ser utilizada para determinar sus caídas de voltaje. A continuación se resumen.

\[V_{7k} \approx 46.67 V \nonumber \]

\[V_{2k} \approx 13.33 V \nonumber \]

\[V_{10k} \approx 33.33 V \nonumber \]

\[V_{12k} = V_{24k} \approx 26.67 V \nonumber \]

Finalmente, para determinar lo\(V_{ac}\) sabemos\(V_{ac} = V_a − V_c\), y por observación\(V_a\) es la caída a través de los 2 k\( \Omega \) mientras que\(V_c\) es la caída a través del\( \Omega \) combo de 12 k\( \Omega \)\(||\) 24 k.

\[V_{ac} = V_a−V_c \nonumber \]

\[V_{ac} \approx 13.33V−26.67 V \nonumber \]

\[V_{ac} \approx −13.33 V \nonumber \]

No dejes que el signo negativo sea molesto. Todo lo que indica es que el nodo\(a\) está a un potencial menor que el nodo\(c\), es decir, ese nodo\(a\) está 13.33 voltios por debajo del nodo\(c\). También es puramente casual que\(V_{ac}\) y\(V_a\) tengan la misma magnitud. En el laboratorio, si se conecta un voltímetro de tal manera que el cable rojo (positivo) se une al nodo\(a\) y el cable negro (negativo o de referencia) está unido al nodo\(c\), el medidor mostrará un valor negativo. Si los cables están conectados en reversa, midiendo así\(V_{ca}\), el voltaje se mostrará como positivo (lo que significa que el nodo\(c\) es mayor en potencial que el nodo\(a\), la forma inversa de mirar la situación) ¹.

Cualquier Ruta Funciona

En el ejemplo recién terminado se señaló que, por definición,\(V_{ac} = V_a − V_c\), y esto dictaba el método empleado para encontrar dicha tensión. Resulta que esta es solo una de las muchas formas de determinar una tensión de un punto a otro. En general:

\[\text{To find some voltage } V_{XY}, \text{start at point X and proceed along any convenient route to Y, subtracting voltage rises (polarities of − to +) and adding voltage drops (polarities of + to −) along the way.} \nonumber \]

En el ejemplo anterior, una ruta obvia para\(V_{ac}\) sería bajar los 2 k\( \Omega \) y luego subir los 12 k\( \Omega \). Eso da una caída de aproximadamente 13.33 voltios (positivo). Al subir los 12 k se\( \Omega \) produce una subida de aproximadamente 26.67 voltios (negativo). El resultado es aproximadamente −13.33 voltios, como se calculó previamente. La técnica establece que cualquier ruta puede ser utilizada, por ineficiente o loca que pueda ser. Para verificar esto, una ruta impar podría ser subir los 7 k\( \Omega \), bajar por el 1 k\( \Omega \) y fuente, y luego subir a través de los 24 k\( \Omega \). La suma sería − 46.67 − 10 + 70 − 26.67, o aproximadamente −13.33 voltios una vez más. Una manera fácil de recordar si el potencial se agrega o resta es simplemente mirar el signo de polaridad donde se ingresa el componente a lo largo de la ruta elegida.

Escalera R-2R

Como se prometió anteriormente en el capítulo, es hora de mirar una red de escalera. Si bien las escaleras pueden usar cualquier valor de resistencia deseado, ciertas relaciones resultan ser eminentemente prácticas. De particular interés es la escalera R-2R, un ejemplo de la cual se muestra en la Figura 5.4.11 , y que está siendo impulsada por una fuente de corriente. En esta configuración, solo se utilizan dos valores de resistencia diferentes; algún valor inicial y un segundo valor de precisamente el doble de ese tamaño. Como se dibuja en la Figura 5.4.11 , todas las resistencias horizontales usan el valor R (6 k\( \Omega \) aquí) mientras que todas las resistencias verticales usan 2R (12 k\( \Omega \) aquí) con la excepción de la última resistencia, o terminadora, que usa R.

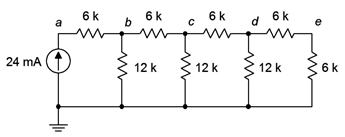
Figura 5.4.11 : Una red de escalera R-2R.

Resulta que esta disposición ofrece algo muy único: una reducción a la mitad de los sucesivos voltajes de los nodos y las corrientes de derivación. Esto es extremadamente útil en circuitos de conversión digital a analógico; el tipo de hardware que convertiría los bits digitales de un archivo MP3 o WAV en señales analógicas escuchables para alimentar altavoces o auriculares.

Así es como funciona. Comenzando en el extremo derecho, debería ser obvio que las dos últimas\( \Omega \) resistencias de 6 k comprenden un divisor de voltaje de 50%, y así\(V_e\) serán la mitad de\(V_d\). La combinación de las tres resistencias finales funciona a 12 k\( \Omega \)\(||\) (6 k\( \Omega \) + 6 k\( \Omega \)), o 6 k\( \Omega \) nuevamente. Así, el divisor de\(c\) a también\(d\) es 50%. Este proceso se repite a medida que nos movemos hacia la izquierda, cada equivalente trabajando a R y dando como resultado un divisor de voltaje del 50%. No importará qué valor se elija para R. Siempre y cuando se utilice 2R para el otro conjunto de resistencias, el resultado siempre serán sucesivos divisores de voltaje del 50%.

Ejemplo 5.4.5

Determine todos los voltajes de nodo con letras en el circuito de la Figura 5.4.11 .

Continuando con el análisis previo, toda la red de resistencias presenta una resistencia equivalente de 12 k\( \Omega \). El\(a\) voltaje del nodo está determinado por la ley de Ohm:

\[V_a = I \times R \nonumber \]

\[V_a = 24mA \times 12 k \Omega \nonumber \]

\[V_a = 288 V \nonumber \]

El análisis previo indicó que los voltajes de nodo subsiguientes deben ser, de izquierda a derecha, 144 voltios, 72 voltios, 36 voltios y 18 voltios. A continuación se realiza una comprobación rápida. La fuente de 24 mA fluye hacia los 6 k más a la izquierda\( \Omega \), produciendo una caída de 144 voltios según la ley de Ohm. Esto se puede restar de\(V_a\) (288 V) para llegar\(V_b\), o 144 voltios, o la mitad del voltaje del nodo anterior, como se esperaba. La corriente a través de la resistencia vertical más a la izquierda debe ser\(V_b\) /12 k\( \Omega \), o 12 mA. Esa es la mitad de la corriente entrante, como se esperaba. KCL indica que la corriente restante, 24 mA − 12 mA, o 12 mA, debe estar fluyendo hacia el segundo 6 k\( \Omega \) entre nodos\(b\) y\(c\). Esto producirá una caída de voltaje de 72 voltios a través de esa resistencia. Es decir,\(V_c\) debe ser 72 voltios menos que\(V_b\) (144 voltios), o 72 voltios. Esto es la mitad de\(V_b\), como se esperaba. De igual manera, la corriente que fluye hacia abajo a través del segundo 12 k\( \Omega \) debe ser\(V_c\) /12 k\( \Omega \), o 6 mA, una vez más la mitad de la corriente anterior, como se esperaba. El proceso continúa a medida que avanzamos hacia la derecha, cada nodo posterior ve la mitad del voltaje del nodo anterior y cada corriente se corta por la mitad también.

Simulación por Computadora

Para verificar los resultados del Ejemplo 5.4.4 , el circuito de escalera R-2R se introduce en un simulador, como se muestra en la Figura 5.4.12 . Los nodos numerados del 1 al 5 en el esquema de simulación corresponden a los nodos con letras del circuito original,\(a\) a través\(e\), respectivamente. Este es un ejemplo donde el uso de instrumentos virtuales resultaría en una pantalla muy desordenada con cinco multímetros. En consecuencia, la simulación utiliza un análisis de punto operativo DC con una sola ventana de salida, como se muestra en la Figura 5.4.13 .

Aunque los números de nodo no están en orden ascendente, los voltajes coinciden perfectamente con los resultados calculados previamente. Cada nodo sucesivo ve la mitad del voltaje del nodo anterior. Aunque no se menciona explícitamente aquí, debería ser obvio que las corrientes también se cortarán a la mitad al progresar de izquierda a derecha, mediante una rápida aplicación de la ley de Ohm.

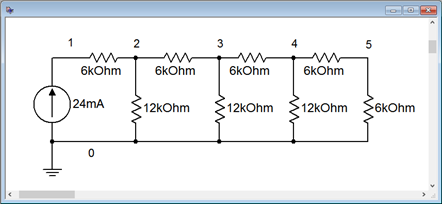
Figura 5.4.12 : El circuito de Ejemplo 5.4.3 en un simulador.

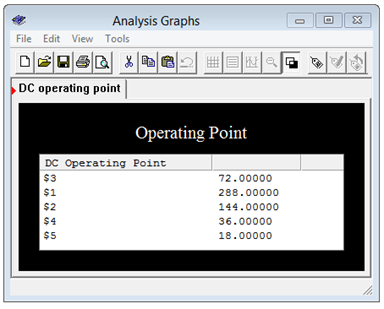
Figura 5.4.13 : Resultados de simulación del circuito de Ejemplo 5.4.4 .

Puentes

Un puente es una configuración particular serie-paralelo que consiste en dos pares de elementos conectados en serie colocados en paralelo. Un ejemplo de un puente resistivo siendo accionado por una fuente de voltaje se muestra en la Figura 5.4.14 . En este circuito,\(R_1\) y\(R_2\) crear una conexión en serie mientras\(R_2\) y\(R_3\) crear la otra. Los dos pares se colocan entonces en paralelo. Si bien este circuito se muestra con una fuente de voltaje, también podría ser accionado por una fuente de corriente. También podrían agregarse otros elementos.

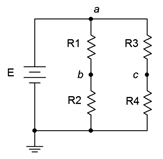
Figura 5.4.14 : Una red de puente resistivo.

Un uso típico de un puente es la medición de alguna cantidad ambiental. Como se indica en el Capítulo 2, existen ciertos dispositivos resistivos que son sensibles al cambio ambiental. Los ejemplos incluyen fotorresistencias, cuya resistencia es una función del nivel de luz; y termistores, cuya resistencia es una función de la temperatura.

Para entender la operación, los voltajes\(V_b\) y\(V_c\) son establecidos por los divisores de voltaje compuestos por\(R_1\) y\(R_2\); y\(R_3\) y\(R_4\), respectivamente. Con las resistencias ordinarias, estos voltajes serían invariables y por lo tanto también\(V_{bc}\) serían de valor fijo. Lo configuraremos de tal manera que\(V_b\) y\(V_c\) sean el mismo voltaje, y así\(V_{bc}\) será cero. Ahora supongamos que reemplazamos\(R_1\) con una fotorresistencia. A medida que aumenta el nivel de luz, su resistencia disminuye. Esto provocará\(V_b\) que suban lo que provocará\(V_{bc}\) que vaya positivo. Si el nivel de luz disminuye, la resistencia de\(R_1\) aumentará, obligando\(V_b\) a caer lo que provocará que\(V_{bc}\) vaya negativo. Cuanto mayor sea el cambio en la luz, mayor\(V_{bc}\) será, y su signo indica si el nivel de luz ha aumentado o disminuido en comparación con el punto de ajuste original. Simplemente colocando alguna forma de voltímetro entre puntos\(b\) y\(c\), podemos crear una pantalla que indique niveles de luz.

Si queremos voltear el letrero, colocaríamos la fotorresistencia en la posición de en\(R_2\) lugar de\(R_1\). Además, es posible aumentar la sensibilidad mediante el uso de sensores en esquinas opuestas (por ejemplo,\(R_1\) y\(R_4\)), y las mediciones comparativas o diferenciales son posibles usando ambos lados (por ejemplo,\(R_1\) con\(R_3\)).

Ejemplo 5.4.6

Determinar\(V_{bc}\) en el circuito de la Figura 5.4.15 .

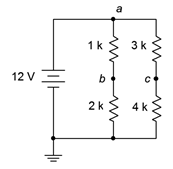
Figura 5.4.15 : Circuito por ejemplo 5.4.5 .

Quizás la forma más sencilla de hacerlo es tratar cada mitad como un divisor de voltaje y luego restarlo\(V_c\) de\(V_b\).

\[V_b = E \frac{R_2}{R_2+R_1} \nonumber \]

\[V_b = 12V \frac{2k \Omega}{2k \Omega +1k \Omega} \nonumber \]

\[V_b = 8V \nonumber \]

\[V_c = E \frac{R_4}{R_4+R_3} \nonumber \]

\[V_c = 12 V \frac{4k \Omega}{ 4k \Omega +3k \Omega} \nonumber \]

\[V_c \approx 6.857V \nonumber \]

Así,\(V_{bc}\) es de 8 voltios menos 6.857 voltios, o 1.143 voltios.

Simulación por Computadora

Para verificar los resultados del Ejemplo 5.4.5 , la red puente de la Figura 5.4.15 se introduce en un simulador, como se muestra en la Figura 5.4.16 .

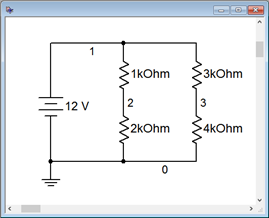
Figura 5.4.16 : El circuito de Ejemplo 5.4.5 en un simulador.

Se ejecuta un análisis de punto de funcionamiento DC y los resultados se muestran en la Figura 5.4.17 . Los voltajes son precisamente los esperados.

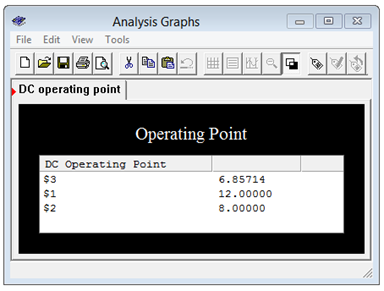
Figura 5.4.17 : Resultados de simulación para el circuito puente del Ejemplo 5.4.5 .

Comentarios Finales

Las técnicas de simplificación serie-paralelo no funcionarán para todos los circuitos. Los circuitos multifuente complejos y algunas redes resistivas como las configuraciones delta o las configuraciones de puente de cinco elementos requieren otras técnicas que se abordarán en capítulos posteriores.

Referencias

¹ O bien, si prefieres esta situación planteada como una pregunta: Cuando estás de pie normalmente, ¿tu cabeza está por encima de tus pies o tus pies están debajo de tu cabeza? Respuesta: ¡Sí!