5.3: Simplificación de componentes serie-paralelo

Podemos ir más allá de las simples observaciones presentadas anteriormente. Precisamente cómo abordemos esto dependerá de los componentes representados por los bloques (la mayoría de las veces resistencias, pero posiblemente una fuente de voltaje o una fuente de corriente) y cómo se conecten entre sí. Para empezar, si todos los elementos de un subcircuito son del mismo tipo, solo se pueden combinar utilizando las técnicas discutidas en los capítulos anteriores. Se agregan resistencias en serie, al igual que las fuentes de voltaje en serie, desconfían de la polaridad. Las resistencias en paralelo se combinan usando la conductancia o la regla producto-suma mientras se agregan fuentes de corriente paralelas, nuevamente desconfiando de la polaridad. Las cosas se ponen un poco más complicadas cuando hay una mezcla, como dos resistencias en serie con una fuente de voltaje, o una resistencia en paralelo con un par de fuentes de corriente. Precisamente cómo se maneja este tipo de situaciones se hará evidente en breve.

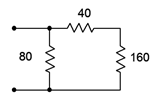
Figura 5.3.1 : Una simple red de resistencias serie-paralelo.

Para ilustrar, consideremos la configuración de resistencia presentada en la Figura 5.3.1 . Imagina que un ohmímetro está conectado a los dos terminales abiertos. ¿Qué leería? El ohmímetro aplicaría una pequeña corriente al circuito para determinar la resistencia efectiva del grupo. Las tres resistencias que se muestran aquí no son una configuración simple en serie porque podemos identificar una división de corriente en las\(\Omega\) resistencias 40\(\Omega\) y 80. De igual manera, no es una red paralela porque las\(\Omega\) resistencias 40\(\Omega\) y 160 no están ambas atadas a los mismos dos nodos. Lo que podemos decir es que las\(\Omega\) resistencias 40\(\Omega\) y 160 están en serie entre sí ya que cada una debe ver la misma corriente. Así, podemos combinar los dos en una sola resistencia equivalente de 200\(\Omega\). Este equivalente está en paralelo con la\(\Omega\) resistencia 80 y 80\(||\) 200 es aproximadamente 57.14\(\Omega\). Eso es lo que debería leer el ohmímetro. En efecto, dondequiera que veamos esta configuración con estos valores precisos, podemos reemplazarla por una sola resistencia de 57.14\(\Omega\).

La técnica de simplificación se puede esbozar de la siguiente manera:

• Identificar subgrupos de resistencias que exhiben configuraciones en serie o paralelas dentro de ellas mismas.
• Reemplazar los subgrupos con una sola resistencia equivalente.
• Repita los pasos anteriores hasta que el circuito se reduzca a una sola resistencia, o alternativamente, a una configuración simple solo en serie o solo en paralelo.

La naturaleza de lazo de la técnica descrita anteriormente puede necesitar ser invocada muchas veces, dependiendo de la complejidad de la red. En redes más simples, un solo paso puede ser suficiente. Inicialmente, puede ser prudente redibujar el circuito para cada iteración del bucle. Eventualmente, con la práctica, esto no será necesario excepto con las redes más complejas. Veamos un ejemplo algo más involucrado.

Ejemplo 5.3.1

Una red de resistencias serie-paralelo se muestra en la Figura 5.3.2 . Determinar su resistencia equivalente.

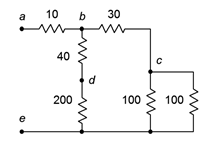
Figura 5.3.2 : Red por ejemplo 5.3.1 .

El primer paso es reconocer aquellos subgrupos que están en serie o en paralelo consigo mismos. Un candidato obvio es que las dos 100\(\Omega\) resistencias están en paralelo entre sí. Dos resistencias de igual valor en paralelo equivalen a la mitad de la resistencia, o 50\(\Omega\) en este caso.

El otro candidato es el\(\Omega\) par 40\(\Omega\), 200. Estos están en serie. La resistencia equivalente del par es la combinación en serie, o 240\(\Omega\).

No hay otros subconjuntos de resistencias que se puedan reducir (todavía). La red se vuelve a dibujar en la Figura 5.3.3 con las resistencias equivalentes. Ahora se repite el proceso.

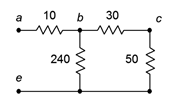
Figura 5.3.3 : Red parcialmente simplificada.

En la red recién reducida, las\(\Omega\) resistencias 50\(\Omega\) y 30 están en serie, produciendo 80\(\Omega\).

Sin volver a dibujar, el proceso puede repetirse nuevamente, esta vez el 240\(\Omega\) estando en paralelo con el nuevo 80\(\Omega\) equivalente. 240\(||\) 80 es igual a 60\(\Omega\). Esta secuencia ha reducido las tres resistencias más a la derecha a una: la nueva 60\(\Omega\) equivalente.

Finalmente, el\(\Omega\) equivalente 60 está en serie con la\(\Omega\) resistencia 10, produciendo una resistencia equivalente final de 70\(\Omega\).

Escaleras

Una escalera es una configuración única serie-paralelo. Se dispone en una cascada de conexiones en serie y paralelas. Las escaleras se utilizan en una variedad de aplicaciones, una de las cuales se examinará en la siguiente sección.

El nombre es obvio en base a la apariencia de la red. Un ejemplo de red de escalera resistiva se muestra en la Figura 5.3.4 . Lo principal a tener en cuenta es que la red de escaleras consiste en “secciones que cargan secciones” repetidamente. Por carga, queremos decir que este elemento (la carga) extrae corriente y potencia de la sección anterior. Como resultado, no se pueden usar divisores de voltaje simples de dos resistencias. Por ejemplo, es un error común asumir eso\(R_1\) y\(R_2\) crear un divisor de voltaje que pueda usarse para determinar\(V_{bf}\) si\(V_{af}\) se conoce. Del mismo modo, los no iniciados pueden creer incorrectamente eso\(R_3\) y\(R_4\), o\(R_5\) y\(R_6\) crear divisores de voltaje.

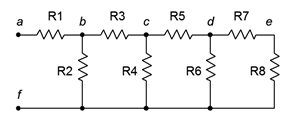
Figura 5.3.4 : Una red de escalera resistiva.

De hecho, el único divisor de voltaje adecuado en esta configuración es entre\(R_7\) y\(R_8\). La razón de esto se hace evidente si imaginamos determinar la resistencia equivalente de la red colocando un ohmímetro en terminales\(a\) y\(f\). El ohmímetro aplicará una corriente al nodo\(a\) que pasa a través\(R_1\). En el nodo\(b\) esta corriente se divide, parte bajando\(R_2\) y parte continuando a través\(R_3\). Claramente entonces,\(R_1\) y no\(R_2\) están en serie ya que no ven la misma corriente. Además, la corriente que fluye a través\(R_3\) ingresa al nodo\(c\) donde se divide de nuevo, parte hacia abajo\(R_4\) con el resto fluyendo a través\(R_5\). Así,\(R_3\) y tampoco\(R_4\) están en serie. El mismo tipo de cosas vuelve a ocurrir en el nodo\(d\). Esto continuaría por tantos peldaños como estén en la escalera, siendo la única excepción las dos últimas resistencias que están en serie (\(R_7\)y\(R_8\) aquí).

¿Cómo entonces encontramos la resistencia equivalente de esta red? Comenzamos en el extremo más alejado de las terminales abiertas. Ya lo hemos señalado\(R_7\) y\(R_8\) están en serie. Este par, si se trata como una sola resistencia, está en paralelo con\(R_6\), o\(R_6||(R_7+R_8)\). Este grupo de tres está en serie con\(R_5\), rindiendo\(R_5+R_6||(R_7+R_8)\) ¹. Este nuevo grupo de cuatro está en paralelo con\(R_4\), cediendo\(R_4||(R_5+R_6||(R_7+R+8))\). Este grupo está en serie con\(R_3\), y ese nuevo grupo está a su vez en paralelo con\(R_2\). Por último, esa penúltima agrupación está en serie con\(R_1\). Por lo tanto, la resistencia equivalente de la red es\(R_1+R_2||(R_3+ R_4||(R_5+R_6||(R_7+R_8)))\). Seguramente, es un poco tedioso calcular el valor, pero particularmente difícil. Una palabra para el sabio: si el objetivo es determinar los voltajes en los diversos nodos o la miríada de corrientes de ramificación, será útil realizar un seguimiento de las resistencias equivalentes de los diversos agrupamientos. Por ejemplo, si\(V_{cf}\) se conoce y el objetivo es encontrar\(V_{df}\), el divisor de voltaje sería\(R_6||(R_7+R_8) / (R_5+R_6||(R_7+R_8))\).

Ejemplo 5.3.2

Una red de escalera resistiva se muestra en la Figura 5.3.5 . Determinar su resistencia equivalente.

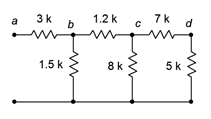
Figura 5.3.5 : Red por ejemplo 5.3.2 .

Comenzando en el extremo más alejado de los terminales abiertos, observamos que las\(\Omega\) resistencias de 7 k\(\Omega\) y 5 k están en serie, produciendo 12 k\(\Omega\). Esto es en paralelo con el 8 k\(\Omega\). 12 k\(||\) 8 k es 4.8 k\(\Omega\). Esto está en serie con los 1.2 k\(\Omega\) rindiendo 6 k\(\Omega\). El\(\Omega\) equivalente a 6 k está en paralelo con el 1.5 k\(\Omega\) que rinde 1.2 k\(\Omega\).

Finalmente, el\(\Omega\) equivalente a 1.2 k está en serie con los 3 k\(\Omega\), produciendo una resistencia equivalente final de 4.2 k\(\Omega\).

Recuerde, siempre comience por el otro extremo y trabaje hacia los terminales abiertos, es decir, los terminales en los que está tratando de encontrar la resistencia equivalente.

Ejemplo 5.3.3

Una red de escalera resistiva se muestra en la Figura 5.3.6 . Determinar su resistencia equivalente.

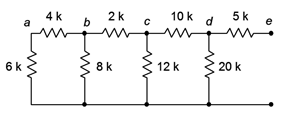
Figura 5.3.6 : Red por ejemplo 5.3.3 .

El extremo más alejado de los terminales abiertos es el extremo izquierdo. Primero, las\(\Omega\) resistencias de 6 k\(\Omega\) y 4 k están en serie, produciendo 10 k\(\Omega\). Esto es paralelo a los 8 k\(\Omega\), logrando aproximadamente 4.444 k\(\Omega\). A su vez, esto es en serie con los 2 k\(\Omega\) rindiendo 6.444 k\(\Omega\). Ese resultado es paralelo a los 12 k\(\Omega\) que rinde 4.193 k\(\Omega\). Al colocarlo en serie con la\(\Omega\) resistencia de 10 k, se obtienen 14.193 k\(\Omega\). Esto es en paralelo con los 20 k\(\Omega\) rindiendo 8.302 k\(\Omega\).

Finalmente, el\(\Omega\) equivalente de 8.302 k está en serie con los 5 k\(\Omega\), produciendo una resistencia equivalente final de aproximadamente 13.3 k\(\Omega\).

Referencias

¹ Recordemos que\(||\) tiene mayor precedencia que + o —, por lo tanto\(||\) se realiza primero, más bien como la multiplicación cuando se mezcla con suma y resta.