7.2: Análisis ganglionar

El análisis ganglionar es una técnica que se puede aplicar a prácticamente cualquier circuito. En general, podría considerarse una técnica de solución universal ya que no hay configuraciones prácticas de circuito que no pueda manejar. El análisis nodal se basa en la aplicación de la ley actual de Kirchhoff para crear una serie de ecuaciones de nodos que pueden resolverse para voltajes de nodo. Estas ecuaciones se basan en la ley de Ohm y serán de la forma\(I = V/R\), o más generalmente,\(I = (1/RX) \cdot VA + (1/RY) \cdot VB \dots\) Una vez que se obtengan los voltajes de los nodos, encontrar cualquier corriente de rama o potencias de componentes se convierte en un ejercicio casi trivial. Examinaremos dos variaciones; una versión general que se puede usar tanto con fuentes de voltaje como de corriente, y una segunda versión algo más rápida que puede usarse con circuitos solo accionados por fuentes de corriente.

Método General

Considere el circuito que se muestra en la Figura 7.2.1 . Comenzamos etiquetando los nodos de conexión y asignando direcciones actuales. Nos interesan particularmente los cruces actuales, es decir, los lugares donde las corrientes pueden combinarse o dividirse. Estos también se conocen como nodos sumadores y están rodeados en verde en la figura. Las direcciones actuales se eligen arbitrariamente y pueden ser lo contrario de la realidad. Esto no es un problema. Si asignamos direcciones que están equivocadas, las direcciones resultantes finalmente se mostrarán invertidas pero los voltajes de los nodos calculados estarán bien.

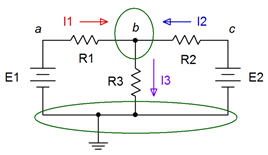
Figura 7.2.1 : Circuito básico de fuente de doble voltaje con corrientes y nodos definidos.

Se elige un nodo como referencia. Este es el punto al que se medirán todos los demás voltajes de los nodos. Normalmente, el nodo de referencia es tierra, aunque no tiene que serlo.

Ahora escribimos una ecuación de suma actual para cada nodo de suma, excepto para el nodo de referencia. En este circuito solo hay un nodo donde se combinan las corrientes (que no sean tierra) y ese es nodo\(b\). Puntos\(a\) y\(c\) son lugares donde los componentes se conectan, pero no son nodos sumando, por lo que podemos ignorarlos por ahora. Usando KCL en el nodo\(b\) podemos decir:

\[I_1 + I_2 = I_3 \nonumber \]

A continuación, describimos estas corrientes en términos de los voltajes de los nodos y componentes asociados a través de la ley de Ohm. Por ejemplo,\(I_3\) es el\(b\) voltaje del nodo dividido por\(R_3\) mientras\(I_1\) es el voltaje\(R_1\) dividido por\(R_1\). Este voltaje es\(V_a − V_b\). Por lo tanto,

\[\frac{V_a −V_b}{R_1} + \frac{V_c −V_b}{R_2} = \frac{V_b}{R_3} \nonumber \]

Señalando que\(\frac{V_a = E_1}\) y\(\frac{V_c = E_2}\), con un poco de álgebra esto puede reducirse a una serie de productos de conductancias y voltajes:

\[\left( \frac{1}{R_1} \right) E_1 + \left( \frac{1}{R_2} \right) E_2 = \left( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \right) V_b \nonumber \]

Todas las cantidades son conocidas excepto por\(V_b\) y así se encuentra fácilmente con un poco más de álgebra. Como veremos, este formato de producto conductancia-voltaje resulta ser una manera conveniente de escribir estas ecuaciones. También, tenga en cuenta que los dos primeros términos de la izquierda se reducen a valores actuales fijos. Si hubiera habido más nodos, habría habido más ecuaciones, una por cada nodo.

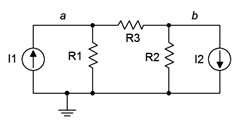
Figura 7.2.2 : Circuito básico de fuente de corriente dual.

Para las fuentes de corriente, es posible un enfoque más directo. Considera el circuito de la Figura 7.2.2 . Comenzamos como antes, identificando nodos y etiquetando corrientes. Esto se muestra en la Figura 7.2.3 . Luego escribimos ecuaciones de suma actuales en cada nodo (excepto para tierra). Consideramos que las corrientes que entran en un nodo son positivas y que salen como negativas.

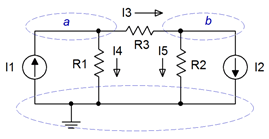
Figura 7.2.3 : Circuito básico de fuente de corriente dual con corrientes y nodos definidos.

\[\text{Node } a: I_1 = I_3 + I_4 \nonumber \]

\[\text{Node } b: I_3 = I_2 + I_5, \text{ and rearranging in terms of the fixed source,} \nonumber \]

\[\text{Node } b: −I_2 = −I_3 + I_5 \nonumber \]

Las corrientes son luego descritas por sus equivalentes de ley de Ohm:

\[\text{Node } a: I_1 = \frac{V_a −V_b}{R_3} + \frac{V_a}{R_1} \nonumber \]

\[\text{Node } b: −I_2 = − \frac{V_a −V_b}{R_3} +\frac{V_b}{R_2} \nonumber \]

Ampliando y recogiendo términos rendimientos:

\[\text{Node } a: I_1 = \left( \frac{1}{R_1} + \frac{1}{R_3} \right) V_a − \left( \frac{1}{R_3} \right) V_b \nonumber \]

\[\text{Node } b: −I_2 =− \left( \frac{1}{R_3} \right) V_a + \left( \frac{1}{R_3} + \frac{1}{R_2} \right) V_b \nonumber \]

Como se conocen los valores y las corrientes de resistencia, se pueden usar técnicas de solución de ecuaciones simultáneas para resolver las tensiones de los nodos. Una vez más, habrá tantas ecuaciones como voltajes de nodo. Es muy importante que los términos “se alineen” cuando se escribe el sistema final de ecuaciones. Es decir, debería haber una columna para los\(V_a\) términos, una columna para los\(V_b\) términos, y así sucesivamente. No deben escribirse en orden aleatorio. Este formato hará que sea mucho más fácil ingresar los coeficientes en una calculadora o resolverlos manualmente.

Ejemplo 7.2.1

Determine\(V_b\) en el circuito de la Figura 7.2.4 .

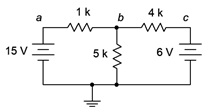
Figura 7.2.4 : Circuito por ejemplo 7.2.1 .

Este circuito cuenta con dos nodos sumadores de corriente, tierra y nodo\(b\). Supongamos que las corrientes de las dos fuentes fluyen hacia el nodo\(b\) y la corriente de salida fluye hacia abajo a través de la\( \Omega \) resistencia de 5 k. Será conveniente si encontramos los equivalentes de conductancia de las resistencias antes de continuar. Tomando los recíprocos encontramos: 1 k\( \Omega \) = 1 mS, 4 k\( \Omega \) = 0.250 mS, y 5 k\( \Omega \) = 0.2 mS. A través de KCL podemos decir:

\[I_{1k} + I_{4k} = I_{5k} \nonumber \]

Reemplazar estas corrientes con sus equivalentes de ley de Ohm rinde,

\[\frac{15 V −V_b}{1k \Omega } + \frac{6V −V_b}{4 k \Omega } = \frac{V_b}{5 k \Omega } \nonumber \]

cobrando términos,

\[15mA+1.5mA = \left( \frac{1}{1k \Omega } + \frac{1}{4k \Omega } + \frac{1}{5k \Omega } \right) V_b \nonumber \]

y resolviendo\(V_b\),

\[V_b = \frac{16.5 mA}{1mS +0.25mS +0.2mS} \nonumber \]

\[V_b = 11.379 \text{ volts} \nonumber \]

Al\(V_b\) ser mayor que la fuente de 6 voltios, nuestra supuesta dirección de corriente para la\( \Omega \) resistencia de 4 k era incorrecta; asumimos de derecha a izquierda pero de hecho es de izquierda a derecha, fluyendo de 11.379 voltios a 6 voltios. Como puede ver, esto no presentó ningún problema.

Por razones de comparación, este circuito se resolvió en el Capítulo 6 usando conversiones fuente y también usando superposición.

Método de Inspección

El sistema de ecuaciones se puede obtener directamente a través de la inspección si el circuito no contiene fuentes de voltaje. Para el nodo bajo inspección, suma todas las fuentes de corriente conectadas al mismo para obtener la constante de corriente. El término de conductancia para ese nodo será la suma de todas las conductancias conectadas a ese nodo. Para las conductancias del otro nodo, determinar las conductancias entre el nodo bajo inspección y estos otros nodos. Todos estos términos serán negativos. Como comprobación cruzada, el conjunto de ecuaciones producidas debe exhibir simetría diagonal, es decir, si se dibuja una diagonal de la parte superior izquierda a la inferior derecha a través de los pares conductancia-voltaje, entonces los coeficientes que se encuentran por encima de la diagonal tendrán que coincidir con los que se encuentran debajo de la diagonal a medida que nos movemos perpendiculares de la diagonal. Esto se ilustra en la Figura 7.2.5 . La simetría diagonal se puede ver en el Ejemplo 7.2.1 al anotar los coeficientes coincidentes “\(−1/R_3\)” en el par final de ecuaciones. Como ejemplo del método de inspección, centrándonos en el nodo\(a\) en la Figura 7.2.2 , encontramos la fuente de corriente fija\(I_1\) alimentándolo (ingresando, por lo tanto positiva). Las conductancias conectadas directamente al nodo\(a\) son\(1/R_1\) y\(1/R_3\), produciendo el coeficiente para\(V_a\). La única conductancia común entre nodos\(a\) y\(b\) es\(1/R_3\), produciendo el\(V_b\) coeficiente.

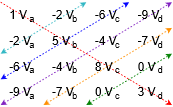
Figura 7.2.5 : Simetría diagonal.

El método de inspección se resume de la siguiente manera:

1. Verifique que el circuito utilice solo fuentes de corriente con resistencias y sin fuentes de voltaje. Si existen fuentes de voltaje, deben ser convertidas a fuentes de corriente antes de continuar.

2. Encuentra todos los nodos sumadores actuales y numerarlos. Decidir también sobre el nodo de referencia (generalmente suelo).

3. Para generar una ecuación, localice el primer nodo. Este es el nodo de interés y los siguientes pasos se asociarán con él.

4. Suma las fuentes de corriente que alimentan el nodo de interés. Entrar se considera positivo mientras que salir se considera negativo. La suma se coloca en un lado del signo igual.

5. A continuación, encuentra todas las resistencias conectadas al nodo de interés y escríbelas como una suma de conductancias en el otro lado del signo igual, multiplicándose el grupo por la tensión de este nodo (e.g.,\(V_1\)).

6. Ahora encuentra todas las resistencias que están conectadas al nodo de interés y a otros nodos (excepto la referencia de tierra). Para cada uno de estos otros nodos, multiplique la suma de las conductancias entre el nodo de interés y este otro nodo por la tensión de este otro nodo, para luego restar ese producto de la ecuación construida hasta ahora. Una vez que se consideran todos los demás nodos, se termina esta ecuación.

7. Encuentra el siguiente nodo y trata esto como el nuevo nodo de interés.

8. Repita los pasos del 4 al 7 hasta que todos los nodos hayan sido tratados como el nodo de interés. Cada iteración crea una nueva ecuación. Habrá tantas ecuaciones como nodos haya, menos el nodo de referencia. Verifique la simetría diagonal y resuelva.

El método de inspección se observa mejor en acción; como en el siguiente ejemplo.

Ejemplo 7.2.2

Determinar\(V_a\) y\(V_b\) en el circuito de la Figura 7.2.6 . También determinar la corriente que fluye a través de la\( \Omega \) resistencia 100.

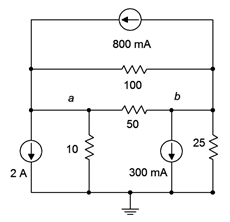
Figura 7.2.6 : Circuito por ejemplo 7.2.2 .

Este circuito cuenta con tres nodos sumadores de corriente; tierra, nodo\(a\) y nodo\(b\). Además, utiliza solo fuentes de corriente y no fuentes de voltaje. Por lo tanto, podemos utilizar el método de inspección para obtener el sistema de ecuaciones (en este caso, dos ecuaciones).

Comenzamos por enfocarnos en el nodo\(a\), nuestro primer nodo de interés. Construiremos la primera expresión pieza por pieza. Primero encontramos las fuentes de corriente que alimentan este nodo:

\[800mA − 2A = \dots \nonumber \]

A continuación, encontramos todas las resistencias conectadas al nodo\(a\) y las escribimos como conductancias, multiplicándose el grupo por voltaje de nodo\(a\):

\[800mA − 2A = \left( \frac{1}{10 \Omega } + \frac{1}{50 \Omega } + \frac{1}{100 \Omega } \right) V_a \dots \nonumber \]

Ahora encuentra todas las resistencias que están conectadas a este nodo y a los demás nodos. Multiplicar esas resistencias (expresadas como conductancias) por las otras tensiones de nodo asociadas y restar los productos de la expresión construida hasta ahora. Repita el procedimiento para todos los nodos restantes excepto la referencia de suelo. En este ejemplo solo hay otro nodo, nodo\(b\), y por lo tanto solo una iteración.

\[800mA −2 A = \left( \frac{1}{10 \Omega } + \frac{1}{50 \Omega } + \frac{1}{100 \Omega } \right) V_a − \left( \frac{1}{50 \Omega } + \frac{1}{100 \Omega } \right) V_b \nonumber \]

Finalmente, simplifique las constantes y coeficientes, y la primera expresión está completa:

\[−1.2 A = 130mS V_a − 30mS V_b \nonumber \]

Ahora repetimos todo el proceso para la siguiente ecuación. Nodo\(b\) es nuestro nuevo nodo de interés. Las fuentes de corriente fija son:

\[−800mA −300 mA = \dots \nonumber \]

A continuación, encontramos todas las resistencias conectadas al nodo\(b\) y las escribimos como conductancias, multiplicándose el grupo por voltaje de nodo\(b\):

\[−800mA −300 mA = \left( \frac{1}{25 \Omega } + \frac{1}{50 \Omega } + \frac{1}{100 \Omega } \right) V_b \dots \nonumber \]

Ahora encontramos todas las resistencias que están conectadas a este nodo y a los demás nodos. Multiplicar esas resistencias (expresadas como conductancias) por estas otras tensiones de nodo y restar esos productos de la expresión construida hasta ahora. Asegúrese de que los términos se alineen verticalmente en función de los voltajes de los nodos.

\[−800mA −300 mA = − \left( \frac{1}{50 \Omega } + \frac{1}{100 \Omega } \right) V_a+ \left( \frac{1}{25 \Omega } + \frac{1}{50 \Omega } + \frac{1}{100 \Omega } \right) V_b \nonumber \]

Finalmente, simplifique las constantes y coeficientes, y esta expresión es completa:

\[−1.1 A =−30 mS V_a +70 mS V_b \nonumber \]

Ahora tenemos dos ecuaciones con dos incógnitas. Vamos a verificar si hay simetría diagonal:

\[−1.2 A = 130mS V_a − 30mS V_b \nonumber \]

\[−1.1 A = −30 mS V_a + 70 mS V_b \nonumber \]

El coeficiente perpendicular es de −30 mS en cada lado. Ahora podemos resolver el sistema. Los resultados son\(V_a\) = −14.27 voltios y\(V_b\) = −21.83 voltios. La corriente que fluye a través de la resistencia 100 es (−14.27 V − (−21.83 V)) /100\( \Omega \), o aproximadamente 75.6 mA fluyendo de izquierda a derecha.

Verifiquemos que estos valores sean correctos. Podemos realizar una suma de KCL en el nodo\(a\) y ver si se equilibra. Ya sabemos que 2 amperios y 75.6 miliamperios salen mientras entran 800 miliamperios. Sólo necesitamos encontrar las corrientes a través de las\( \Omega \) resistencias 10\( \Omega \) y 50. Primero, observe que el 50\( \Omega \) ve el mismo voltaje que el\( \Omega \) resistor 100. Al ser la mitad de la resistencia, debe producir el doble de corriente, o 151.2 miliamperios que salen. La corriente a través del 10\( \Omega \) se encuentra a través de la ley de Ohm, o −14.27 V/10\( \Omega \), que es 1.427 amperios entrando.

\[\text{Entering: } 0.8 A + 1.427 A = 2.227 A \nonumber \]

\[\text{Exiting: } 2 A + 0.0756 A + 0.1512 A \approx 2.227 A \nonumber \]

KCL está satisfecho. Para completar la verificación realizamos la misma suma en nodo\(b\). Esto se deja como un ejercicio.

Ejemplo 7.2.3

Escribe las ecuaciones de nodo para el circuito de la Figura 7.2.7 .

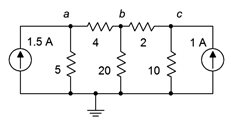
Figura 7.2.7 : Circuito para Ejemplo 7.2.3 .

Este circuito tiene cuatro nodos sumadores de corriente; tierra y nodos\(a\),\(b\), y\(c\). Además, utiliza solo fuentes de corriente y no fuentes de voltaje. Por lo tanto, podemos utilizar el método de inspección para obtener el sistema de ecuaciones (tres ecuaciones).

Como ya hemos visto, terminaremos con valores de conductancia en las ecuaciones finales. Podemos ahorrar algo de trabajo más tarde al encontrar el valor de conductancia de cada resistencia en este momento. El resultado se muestra en la Figura 7.2.8 .

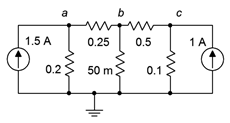
Figura 7.2.8 : Circuito de la Figura 7.2.7 mostrado con conductancias en lugar de resistencias.

Comenzamos por enfocarnos en el nodo\(a\), nuestro primer nodo de interés. Construiremos la primera expresión pieza por pieza. Primero encontramos las fuentes de corriente que alimentan este nodo. Eso es sólo la fuente de 1.5 A, entrar es positivo.

\[1.5A = \dots \nonumber \]

A continuación, encontramos todas las conductancias conectadas al nodo a y multiplicamos por voltaje de nodo a:

\[1.5A = (0.2S +0.25S) V_a \dots \nonumber \]

Encuentra todas las conductancias que están conectadas a este nodo y a los demás nodos. Multiplicar esas conductancias por los otros voltajes de nodo asociados y restar esos productos de la expresión construida hasta ahora. Repita el procedimiento para todos los nodos restantes excepto la referencia de suelo.

\[1.5A = (0.2S +0.25S) V_a −(0.25S) V_b − (0) V_c \nonumber \]

Finalmente, simplifique las constantes y coeficientes, y la primera expresión está completa:

\[1.5A = 0.45S V_a − 0.25S V_b − 0 V_c \nonumber \]

Dejamos el término cero en solo para alineación. Ahora repetimos todo el proceso para la siguiente ecuación. El nodo de interés es ahora nodo\(b\). Aquí está el resultado:

\[0 =−0.25 S V_a +0.8S V_b − 0.5 V_c \nonumber \]

Y finalmente para nodo\(c\) tenemos:

\[1A = 0 V_a − 0.5S V_b +0.6 V_c \nonumber \]

Nuestras tres ecuaciones son (con algo de relleno para ver mejor las columnas):

\[1.5A = 0.45S V_a −0.25S V_b −0 V_c \nonumber \]

\[0 =−0.25 SV_a +0.8SV_b −0.5V_c \nonumber \]

\[1A = −0V_a −0.5SV_b +0.6V_c \nonumber \]

Comprobar simetría diagonal: tenemos pares de −0.25, 0 y −0.5 a ambos lados de la diagonal.

Ahora el sistema de ecuaciones puede resolverse para los tres voltajes de nodo y verificarse usando sumaciones KCL en cada nodo. Esto se deja como un ejercicio.

Conversión de fuentes y otras simplificaciones

Dados los circuitos con fuentes de voltaje, puede ser más fácil convertirlos en fuentes de corriente y luego aplicar la técnica de inspección en lugar de usar el enfoque general esbozado inicialmente. Hay una trampa a tener en cuenta al usar conversiones de fuente: el voltaje a través o la corriente a través de un componente convertido probablemente no será el mismo que el voltaje o la corriente en el circuito original. Esto se debe a que la ubicación del componente convertido habrá cambiado. Por ejemplo, el circuito de la Figura 7.2.9 podría resolverse usando análisis nodal convirtiendo la fuente de voltaje y la resistencia asociada en una fuente de corriente. Es decir, se\(E/R_1\) convertiría en una fuente\(I_3\) con una resistencia paralela\(R_1\). Esto se muestra en la Figura 7.2.10 .

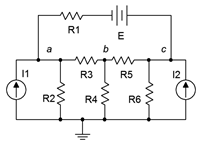
Figura 7.2.9 : Circuito con fuentes de corriente y voltaje.

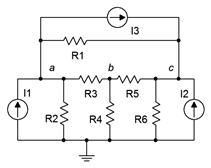
Figura 7.2.10 : Circuito convertido a fuentes de corriente solamente.

Aquí está la trampa: en el circuito convertido, aunque\(R_1\) todavía se conecta al nodo\(a\), el otro extremo ya no se conecta a la fuente de voltaje. Más bien, el lado derecho ahora se conecta al nodo\(c\). Por lo tanto, no es probable que la caída de voltaje\(R_1\) en el circuito convertido sea igual a la caída de voltaje vista\(R_1\) en el circuito original (la única forma en que serían iguales es si\(E\) fuera 0 voltios). En el circuito convertido, los nodos\(a\) y no\(c\) han cambiado del original, por lo que el voltaje original a través se\(R_1\) puede determinar vía\(V_a\),\(V_c\) y\(E\) en el circuito original.

Si un circuito usa fuentes de voltaje exclusivamente, o incluso una proporción muy grande de fuentes de voltaje, una técnica alternativa llamada análisis de malla puede ser una mejor opción que usar numerosas conversiones. El análisis de malla se detallará más adelante en este capítulo.

Un punto final a considerar es simplificar las redes de resistencias para reducir el número de nodos. Menos nodos significa menos ecuaciones y una solución más rápida. Por ejemplo, una parte de una red podría consistir en dos resistencias paralelas que están en serie con una tercera resistencia. Ordinariamente, la unión común de estas tres resistencias constituiría un nodo sumador de corriente y se necesitaría derivar una ecuación para ello. Puede ser más fácil simplemente reemplazar el trío con una sola resistencia que sea igual al valor de combinación serie-paralelo. Esto eliminaría el nodo y simplificaría la creación del sistema de ecuaciones, pero no alteraría el resto del circuito.

Supernodo

En ocasiones puede encontrarse con un circuito como el que se muestra en la Figura 7.2.11 que tiene una fuente de voltaje sin una resistencia en serie asociada a ella. Sin esa resistencia, se vuelve imposible crear una expresión para la corriente que pasa por la fuente usando el método general, e imposible convertir la fuente de voltaje en una fuente de corriente para usar el método de inspección. Una posible forma de salir de este dilema es simplemente agregar una resistencia muy pequeña en serie con él para que sea posible una conversión de fuente. La resistencia en cuestión tendría que ser mucho más pequeña que cualquier resistencia circundante para tener un impacto mínimo en los resultados. Una reducción de dos órdenes de magnitud generaría una variación menor que la producida por las tolerancias de resistencia en todos los circuitos excepto de alta precisión. La otra salida es usar un supernodo.

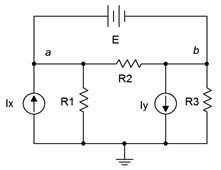
Figura 7.2.11 : Circuito para análisis de supernodos.

Un supernodo es, en efecto, la combinación de dos nodos. Se basa en una simple observación. Si examinamos el circuito de la Figura 7.2.11 , la trayectoria de la fuente de voltaje produce corrientes idénticas que fluyen dentro y fuera de los nodos\(a\) y\(b\). Como consecuencia, si tratamos a los dos nodos como un nodo grande, entonces cuando escribimos una suma KCL, estos dos términos se cancelarán. Para ver cómo funciona esto, consulte la Figura 7.2.12 .

En esta versión hemos sustituido la fuente de voltaje con su resistencia interna ideal, un corto. También hemos etiquetado los dos nodos de interés,\(a\) y\(b\), y etiquetado las corrientes, dibujados con direcciones convenientes.

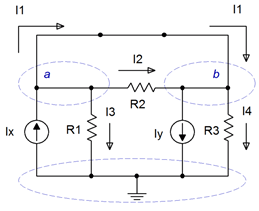
Figura 7.2.12 : Circuito modificado para el análisis de supernodos.

Debido a la fuente de voltaje cortocircuitado, los nodos\(a\) y ahora\(b\) son el mismo nodo. Considera las corrientes que entran y salen de este nodo combinado o “super”. En el lado izquierdo (anteriormente nodo\(a\)) vemos una corriente constante\(I_x\) entrando mientras\(I_1\),\(I_2\) y\(I_3\) estamos saliendo. En el lado derecho (antes nodo\(b\)) vemos\(I_y\) salir junto con\(I_4\), y entrando vemos\(I_1\) y\(I_2\). Ahora vamos a configurar las corrientes de entrada en el lado izquierdo del signo igual con las corrientes de salida a la derecha:

\[\sum I_{in} = \sum I_{out} \nonumber \]

\[I_x+I_1+I_2 = I_y+I_1+I_2+I_3+I_4 \nonumber \]

Esto puede simplificarse para:

\[I_x − I_y = I_3 +I_4 \nonumber \]

Escribiendo esto en términos de la ley de Ohm tenemos:

\[I_x − I_y = \frac{1}{R_1} V_a + \frac{1}{R_3} V_b \nonumber \]

También lo sabemos\(V_a − V_b = E\) por el circuito original. Suponiendo que todas las fuentes y resistencias son conocidas, eso hace dos ecuaciones con dos incógnitas, solucionables mediante técnicas de ecuaciones simultáneas. Esto se ilustra en el siguiente ejemplo.

Ejemplo 7.2.4

Encuentra\(V_a\) y\(V_b\) para el circuito de Figura 7.2.13 .

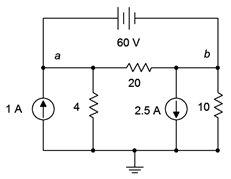
Figura 7.2.13 : Circuito para Ejemplo 7.2.4 .

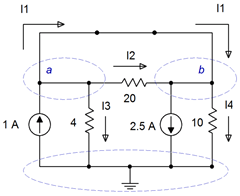
Figura 7.2.14 : Circuito modificado para el análisis de supernodos.

Como se muestra en la Figura 7.2.14 , cortocircuitamos la fuente de 60 voltios y escribimos una suma de corriente en el\(a\)\(b\) supernodo:

\[\sum I_{in} = \sum I_{out} \nonumber \]

\[1A + I_1+I_2 = 2.5 A +I_1+I_2+I_3+I_4 \nonumber \]

Esto puede simplificarse para:

\[−1.5 A = I_3 +I_4 \nonumber \]

Escribiendo esto en términos de la ley de Ohm tenemos:

\[−1.5A = \frac{1}{4 \Omega } V_a + \frac{1}{10 \Omega } V_b \nonumber \]

\[−1.5 A = 0.25S V_a +0.1S V_b \nonumber \]

También sabemos que los\(V_a − V_b = 60\) voltios. Por lo tanto\(V_b = V_a − 60\) voltios. Sustituyendo esto en la ecuación anterior produce:

\[−1.5 A = 0.25S V_a +0.1S(V_a −60 V) \nonumber \]

\[−1.5 A = 0.25S V_a +0.1S V_a −6A \nonumber \]

\[4.5 A = 0.35S V_a \nonumber \]

\[V_a = 12.857 V \nonumber \]

Sabemos que\(V_b\) es 60 voltios por debajo\(V_a\), entonces\(V_b = −47.143\) voltios.

Para verificar, realizaremos una suma de KCL en cada nodo. Para nodo\(a\), suponiendo\(I_1\) salidas como dibujadas:

\[I_1 = 1A − \frac{V_a}{4 \Omega } − \frac{V_a−V_b}{20 \Omega } \nonumber \]

\[I_1 = 1 A− \frac{12.857V}{4 \Omega } − \frac{12.857V−(−47.143 V)}{20 \Omega } \nonumber \]

\[I_1 =−5.2143A \text{ (negative exit means it's entering)} \nonumber \]

Haciendo lo mismo para el nodo\(b\), y asumiendo\(I_1\) entra como dibujado:

\[I_1 = 2.5 A+ \frac{V_b}{10 \Omega } − \frac{V_a−V_b}{20 \Omega } \nonumber \]

\[I_1 = 2.5 A+ \frac{−47.143 V}{10 \Omega } − \frac{12.857V−(−47.143V)}{20 \Omega } \nonumber \]

\[I_1 =−5.2143A \text{ (negative enter means it's exiting)} \nonumber \]

Estas corrientes coinciden, lo que significa que se verifica que la corriente a través de la fuente de voltaje sea la misma en ambos terminales, como debe ser.

Una alternativa a la técnica básica de supernodos es simplemente describir el voltaje de un nodo en términos de otro desde el principio. Esto se ilustra en el siguiente ejemplo.

Ejemplo 7.2.5

Encuentra\(V_a\),\(V_b\) y\(V_c\) para el circuito de Figura 7.2.15 .

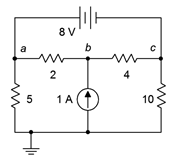
Figura 7.2.15 : Circuito por ejemplo 7.2.5 .

Una vez más tenemos una situación de una fuente de voltaje sin una resistencia en serie. Sin tener que acortarlo y así tratar nodos\(a\) y\(c\) como un supernodo explícito, podemos notar por observación que las corrientes que entran y salen de la fuente de voltaje deben ser idénticas.

El circuito se redibuja en la Figura 7.2.16 con corrientes etiquetadas y usando conductancias equivalentes en lugar de las resistencias. Esta vez la fuente de voltaje se deja adentro.

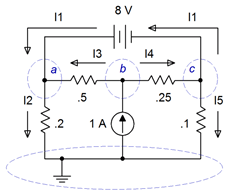
Figura 7.2.16 : Circuito de Ejemplo 7.2.5 con corrientes etiquetadas y usando conductancias.

Comenzamos con la observación de que\(V_c = V_a − 8\) V. En otras palabras,\(V_c\) está bloqueado a\(V_a\) y si encontramos uno de ellos, podemos determinar el otro. Por lo tanto, en lugar de escribir ecuaciones usando tres nodos, en cambio nos referiremos al nodo\(c\) en referencia a nodo\(a\), es decir, escribiremos\(V_a\) − 8 V donde sea que necesitemos\(V_c\). Por lo tanto, este circuito de tres nodos solo necesitará dos ecuaciones.

Comenzamos en el nodo\(a\) y aplicamos KCL como de costumbre.

\[\sum I_{in} = \sum I_{out} \nonumber \]

\[I_1+I_3 = I_2 \nonumber \]

Esto se amplía usando la ley de Ohm y resolvemos para\(I_1\):

\[I_1 = I_2 −I 3 \nonumber \]

\[I_1 = 0.2S V_a −0.5S (V_b −V_a ) \nonumber \]

\[I_1 = 0.7S V_a −0.5S V_b \nonumber \]

En al nodo\(b\):

\[1A = I_3+I_4 \nonumber \]

\[1A = 0.5S(V_b −V_a )+0.25S(V_b −V_c ) \nonumber \]

\[1A = 0.5S(V_b −V_a )+0.25S(V_b −(V_a −8V)) \nonumber \]

\[1A = 0.5S(V_b −V_a )+0.25S(V_b −V_a+8 V) \nonumber \]

\[−1 A =−0.75V_a+0.75V_b \nonumber \]

Y finalmente nodo\(c\):

\[I_4 = I_1+I_5 \nonumber \]

\[I_1 = I_4 −I_5 \nonumber \]

\[I_1 = 0.25S(V_b −V_c )−0.1SV_c \nonumber \]

\[I_1 = 0.25S(V_b −(V_a−8V))−0.1S(V_a −8 V) \nonumber \]

\[I_1 = 0.25S(V_b −V_a+8 V)−0.1S(V_a −8V) \nonumber \]

\[I_1 =−0.35V_a+0.25V_b+2.8A \nonumber \]

Las ecuaciones finales para los nodos\(a\) y\(c\) ambos iguales\(I_1\), es decir, se igualan entre sí. Por lo tanto,

\[0.7SV_a −0.5SV_b = −0.35SV_a+0.25SV_b+2.8 A \nonumber \]

\[2.8 A = 1.05SV_a −0.75SV_b \nonumber \]

Las ecuaciones finales son:

\[2.8A = 1.05SV_a −0.75SV_b \nonumber \]

\[−1 A =−0.75SV_a +0.75SV_b \nonumber \]

La solución es\(V_a = 6\) voltios y\(Vb \approx 4.6667\) voltios. Como\(V_c\) es 8 voltios menos que\(V_a\), luego\(V_c = −2\) voltios.

Simulación por Computadora

Para verificar el resultado del Ejemplo 7.2.5 , el circuito se ingresa a un simulador como se muestra en la Figura 7.2.17 .

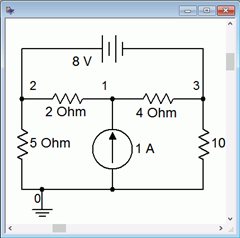
Figura 7.2.17 : Circuito de Ejemplo 7.2.5 en el simulador.

Se ejecuta una simulación de punto de funcionamiento de CC. Los resultados se muestran en la Figura 7.2.18 y coinciden perfectamente con los valores calculados. El nodo 1 corresponde a\(V_b\), el nodo 2 corresponde a\(V_a\) y el nodo 3 corresponde a\(V_c\).

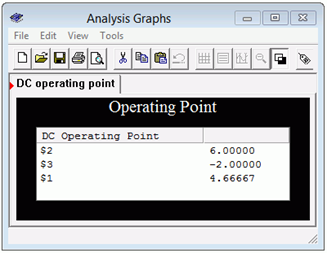
Figura 7.2.18 : Resultados de simulación para el circuito de Ejemplo 7.2.5 .