9.2: Inductancia e inductores

Para comenzar, necesitamos examinar la interrelación entre la corriente eléctrica y los campos magnéticos en un conductor. Cuando una corriente pasa a través de un conductor, como un cable, se crea un campo magnético alrededor del conductor que es proporcional a la intensidad de la corriente. Esto se ilustra en la Figura 9.2.1 .

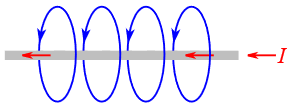
Figura 9.2.1 : Campo magnético alrededor de un conductor.

El campo magnético puede considerarse como conjuntos de anillos concéntricos alrededor del conductor, aunque para mayor claridad solo se dibujan bucles simples en la Figura. El número de líneas magnéticas en un área dada se conoce como el flujo magnético y se le da el símbolo\(\Phi\) (la letra griega phi). La unidad de flujo magnético es el weber, Wb, que lleva el nombre de Wilhelm Weber, un físico alemán del siglo XIX.

\[\text{Magnetic flux } \equiv \text{ the number of magnetic lines enclosed in a given area.} \label{9.1} \]

Tenga en cuenta que el campo magnético recorre la longitud del conductor. La dirección de las líneas de campo sigue la regla de la mano derecha: si agarras el cable con la mano derecha de tal manera que tu pulgar esté apuntando en la dirección del flujo de corriente convencional, entonces tus dedos se envuelven en la dirección del campo magnético. Esta regla se ilustra en la Figura 9.2.2 .

Figura 9.2.2 : Regla de la mano derecha. Fuente de la imagen (modificada)

Si formamos el conductor en un bucle, las líneas de campo se acorralan en el centro del bucle. Esto se ilustra en la Figura 9.2.3 . En este diagrama se puede ver que las líneas efectivamente se recogen en el centro, entrando en la página.

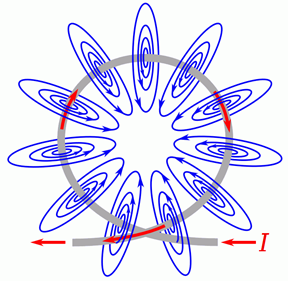
Figura 9.2.3 : Campo magnético alrededor de un bucle.

El efecto de mejora se puede ampliar agregando más bucles en tándem. Esto se conoce como solenoide y se muestra en la Figura 9.2.4 . Es la forma más básica de un inductor.

Figura 9.2.4 : Solenoide.

El efecto de concentración del campo magnético se muestra en la Figura 9.2.5 . En esta figura, la bobina se muestra desde el lado, como una sección transversal de los bucles individuales. Los puntos dentro de los conductores indican que la corriente fluye hacia ti, fuera de la página; mientras que las cruces indican que la corriente está fluyendo hacia la página. Las líneas de flujo salen por la derecha, giran alrededor y vuelven a entrar por la izquierda. Debido al espacio limitado, no se dibuja todo el bucle para cada línea, y es importante recordar que las líneas de flujo magnético no terminan, sino que siempre crean un bucle. Además, aunque aquí se muestra como un plano, este campo es tridimensional, con líneas que vuelven a la página así como al frente de ella.

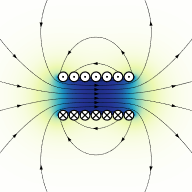
Figura 9.2.5 : Campo magnético en un solenoide. Fuente de la imagen

Así es como se pueden crear los electroimanes ¹. El polo norte es el extremo de salida (lado derecho) de la Figura 9.2.5 mientras que el polo sur es el extremo de entrada (lado izquierdo).

Si la corriente cambia, habrá un cambio proporcional en el campo magnético. Además, este cambio en el campo inducirá una corriente en el conductor que crea un campo magnético que se opone al cambio original en el campo. Esto se conoce como la ley de Lenz. Como alternativa, se puede afirmar que la corriente inducida causada por un campo magnético cambiante se opondrá al cambio en la corriente original que creó ese cambio en el campo magnético original.

En este punto podemos ofrecer una definición adecuada del weber:

\[1 \text{ weber } \equiv \text{ the magnetic flux that, acting on a single loop of a conductor, produces a potential of 1 volt if the flux is reduced to zero at an even rate over 1 second.} \label{9.2} \]

En los circuitos magnéticos también nos interesa la densidad de flujo magnético que es el flujo magnético por unidad de área. El símbolo para la densidad de flujo es\(B\) y tiene unidades de teslas (T), que llevan el nombre de Nicola Tesla, el ingeniero e inventor serbocroata-estadounidense. Un tesla se define como un weber por metro cuadrado.

\[1 \text{ tesla } \equiv 1 \text{ weber} / \text{meter}^2 \label{9.3} \]

Para proporcionar una referencia, la densidad de flujo magnético de la Tierra cerca del ecuador es de aproximadamente 31\(\mu\) T, mientras que el valor de la brecha de la bobina de voz en un altavoz es de alrededor de 1 a 2 T, siendo aún un poco más altos los escáneres médicos de MRI.

Finalmente, llegamos a la definición de inductancia y su unidad, el henry:

\[\text{Inductance is a measure of the tendency of a conductor to oppose a change in the current flowing through it.} \label{9.4} \]

\[1 \text{ henry } \equiv 1 \text{ weber} / 1 \text{ amp} \label{9.5} \]

Como era de esperar, la energía almacenada en el campo magnético de un inductor es proporcional a la inductancia. También es proporcional al cuadrado de la corriente a través del inductor.

\[W = \frac{1}{2} L I^2 \label{9.6} \]

Dónde

\(W\)es la energía en julios,

\(L\)es la inductancia en henries,

\(I\)es la corriente en amperios.

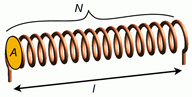
Figura 9.2.6 : Dimensiones simples del inductor de núcleo de aire.

Un inductor en su forma más simple consiste en una serie de bucles de alambre. Estos podrían enrollarse alrededor de un núcleo de hierro, aunque también se podría usar un núcleo no ferroso. Para un inductor simple de una sola capa, como el dibujado en la Figura 9.2.6 , la inductancia se describe mediante la siguiente fórmula:

\[L=\mu \frac{A N^2}{l} \label{9.7} \]

Dónde

\(L\)es la inductancia en henries,

\(\mu\)es la permeabilidad del material del núcleo,

\(A\)es el área de la sección transversal de la bobina,

\(N\)es el número de bobinas o vueltas,

\(l\)es la longitud de la bobina.

Los inductores también pueden enrollarse usando múltiples capas o alrededor de un núcleo toroidal, y estos diseños utilizan fórmulas alternativas.

Estilos de Inductor y Empaque

La ecuación\ ref {9.7} indica que, para lograr una alta inductancia, nos gustaría un núcleo con alta permeabilidad, siendo la permeabilidad una medida de lo fácil que es establecer flujo magnético en dicho material. Sustancias como el hierro o la ferrita tienen una permeabilidad mucho mayor que el aire y se usan comúnmente para núcleos. Tienen la desventaja de que se saturarán antes que un núcleo de aire, y esto puede provocar distorsión.

Figura 9.2.7 : Pastilla eléctrica para bajo.

Otro enfoque es empacar tantas vueltas como sea posible dentro de una longitud dada. Una forma de hacerlo es minimizar el grosor del aislamiento alrededor del cable ². Esto se puede lograr mediante el uso de un revestimiento de esmalte delgado en lugar del aislamiento plástico típico. Un segundo método es usar un alambre muy fino. Esto conduce a dos problemas, a saber, un aumento indeseable en la resistencia en serie equivalente (conocida coloquialmente como resistencia de bobina o\(R_{coil}\)), y una capacidad de carga de corriente limitada. Todos estos efectos tienen que ser equilibrados para lograr el mejor rendimiento para una aplicación determinada.

Los inductores comerciales varían en valor desde una fracción de un nanohenrio para pequeños inductores de “chip” de montaje en superficie hasta varios henries. Algunos dispositivos exhiben grandes inductancias internas a pesar de que no se utilizan específicamente como inductores. Un ejemplo común es un transformador. Otro ejemplo es una pastilla para guitarra eléctrica o bajo, como la que se muestra en la Figura 9.2.7 con su tapa quitada. Unidades como esta pueden construirse de varios miles de vueltas de alambre muy fino (típicamente AWG 41 a 44) y lograr inductancias superiores a un henry.

Una variedad de inductores se muestra en la Figura 9.2.9 , todos los cuales son del tipo de orificio pasante (los inductores de montaje en superficie no aparecen considerablemente diferentes de sus resistencias de montaje en superficie y primos de condensadores).

Figura 9.2.9 : Una colección de inductores.

Las dos unidades hacia la izquierda son inductores moldeados y utilizan un código de color estándar, similar a los utilizados para resistencias y capacitores. La unidad en la parte superior (amarilla) es un inductor de alta corriente que presenta baja\(R_{coil}\). Los tres inductores en el centro utilizan núcleos obvios de ferrita, dos enrollados en núcleos rectos y el tercero enrollado en un núcleo toroidal. La unidad de la derecha utiliza un material de alta permeabilidad en la parte superior y está envuelta en una funda de plástico para protección. Los inductores variables también son una posibilidad y se pueden hacer usando un núcleo de ferrita que puede deslizarse dentro de las bobinas, cambiando efectivamente la permeabilidad del núcleo (parte ferrita, parte aire).

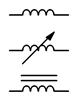
Figura 9.2.10 : Símbolos esquemáticos inductores (arriba-abajo): estándar, variable, núcleo de hierro/ferrita.

Los símbolos esquemáticos para inductores se muestran en la Figura 9.2.10 . El símbolo estándar está en la parte superior. El símbolo inductor variable está en el medio y es un dispositivo de dos cables, algo que recuerda al símbolo de un reóstato. En la parte inferior se encuentra el símbolo de un inductor con un núcleo de hierro, ferrita o similar de alta permeabilidad. En general, al igual que las resistencias, los inductores individuales no están polarizados y no pueden insertarse en un circuito hacia atrás. Sin embargo, existen aplicaciones especiales donde múltiples bobinas se pueden enrollar en un núcleo común, y para estos, la polaridad de su interconexión puede marcar la diferencia.

Hoja de datos del inductor

Una porción de una hoja de datos del inductor se muestra en la Figura 9.2.12 . Esta página enumera los tamaños disponibles de este modelo en particular, cada uno con las cantidades correspondientes. Podemos ver que este modelo está disponible en valores de inductancia que van desde 1\(\mu\) H hasta 100 mH. La tolerancia de los valores más pequeños es de\(\pm\) 10% mientras que los valores a 33\(\mu\) H y superiores están en\(\pm\) 5%. \(Q\)es el factor de calidad y es particularmente importante en los circuitos de CA (siendo mayor mejor), junto con su frecuencia asociada,\(f_Q\). Continuando a través encontramos\(I_R\). Esta es la corriente nominal máxima. Para los valores más pequeños, encontramos que pueden soportar más de 2 amperios mientras que las unidades más grandes pueden soportar solo decenas de miliamperios.

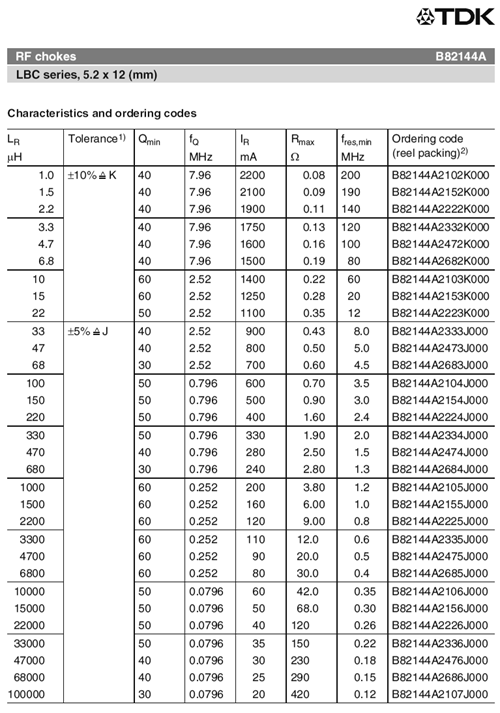
Figura 9.2.12 : Hoja de datos del inductor. Cortesía de TDK

Por último, llegamos a\(R_{max}\). Esto también se conoce como\(R_{coil}\). Representa la resistencia en serie equivalente del inductor. En general, más pequeño es mejor. Para este modelo, va desde una fracción de un ohmio hasta unos pocos cientos de ohmios. Esta tendencia es típica de los inductores; siendo todo lo demás igual, cuanto mayor es la inductancia, mayor es el valor de la resistencia en serie asociada. En muchos circuitos, no se\(R_{coil}\) puede ignorar el valor de.

Inductores en serie y en paralelo

Supongamos que tomamos dos inductores idénticos y los colocamos en serie. Esto efectivamente duplica tanto la longitud como el número de bucles. De la Ecuación\ ref {9.7} podemos ver que duplicar tanto el número de bucles como la longitud duplicaría la inductancia. Esto se debe a que\(N^2\) sube por un factor de cuatro que luego se reduce a la mitad el aumento de la longitud. En consecuencia, los inductores en serie agregan valores al igual que las resistencias en serie. Por extensión, los inductores en paralelo se comportan como resistencias en paralelo. El equivalente de inductores paralelos se puede encontrar usando la regla producto-suma o tomando el recíproco de la suma de sus recíprocos.

Ejemplo 9.2.1

Encuentra la inductancia equivalente de la red que se muestra en la Figura 9.2.11 .

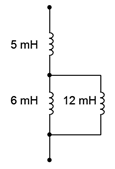
Figura 9.2.11 : Circuito por ejemplo 9.2.1 .

Los inductores de 6 mH y 12 mH están en paralelo. El valor equivalente del par es:

\[L_{parallel} = \frac{L_2 L_3}{L_2+L_3} \nonumber \]

\[L_{parallel} = \frac{6 mH12 mH}{6 mH+12 mH} \nonumber \]

\[L_{parallel} = 4mH \nonumber \]

Esta combinación está en serie con el inductor de 5 mH. Por lo tanto, la inductancia equivalente total es de 4 mH + 5 mH, o 9 mH.

Relación Corriente-Voltaje

La relación corriente-voltaje fundamental del inductor es la imagen especular de la del condensador:

\[\mathcal{v} = L \frac{di}{dt} \label{9.8} \]

Esto establece que el voltaje a través del inductor es una función de la rapidez con la que cambia la corriente. Si la corriente no está cambiando (es decir, en estado estacionario), entonces el voltaje a través del inductor es cero. En este caso, el inductor se comporta como un corto, o más exactamente, como su\(R_{coil}\) valor. Por el contrario, durante un cambio de corriente inicial rápido, el voltaje del inductor puede ser grande, y así el inductor se comporta como un circuito abierto.

Si reorganizamos la Ecuación\ ref {9.8} y resolvemos para la tasa de cambio de corriente, encontramos que:

\[\frac{di}{dt} = \frac{\mathcal{v}}{L} \label{9.9} \]

Por lo tanto, si un inductor es alimentado por una fuente de voltaje constante, la corriente subirá a una tasa constante igual a\(\mathcal{v}/L\). Por ejemplo, considerando el circuito en la Figura 9.2.11 , vemos una fuente de voltaje que alimenta a un solo inductor. Si tuviéramos que trazar la corriente del inductor a lo largo del tiempo, veríamos algo así como el gráfico de la Figura 9.2.12 .

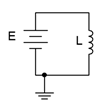
Figura 9.2.11 : Inductor con fuente de voltaje.

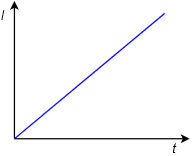
Figura 9.2.12 : Corriente del inductor versus tiempo.

A medida que avanza el tiempo, la corriente a través del inductor aumenta, fluyendo de arriba a abajo. Con un inductor y una fuente teóricamente perfectos, esto continuaría mientras el circuito estuviera energizado. En realidad, esta línea comenzaría a desviarse horizontalmente a medida que la fuente alcanzara sus límites, o bien el inductor fallaría una vez que se alcanzara su máxima corriente o manejo de potencia. La pendiente de esta línea viene dictada por el tamaño de la fuente de voltaje aplicada y la inductancia.

Ejemplo 9.2.2

Determinar la tasa de cambio de corriente a través del inductor en el circuito de la Figura 9.2.13 . También determine la corriente del inductor 10 microsegundos después de que se encienda la energía.

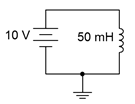
Figura 9.2.13 : Circuito por ejemplo 9.2.2 .

De la Ecuación\ ref {9.9}, la tasa de cambio de corriente es:

\[\frac{di}{dt} = \frac{\mathcal{v}}{L} \nonumber \]

\[\frac{di}{dt} = \frac{10V}{50 mH} \nonumber \]

\[\frac{di}{dt} = 200 A \text{ per second} \nonumber \]

Es decir, por cada segundo, la corriente sube otros 200 amperios. Así, después de apenas 10 microsegundos habrá subido a 200 A/s por 10\(\mu\) s, o 2 mA.

La ecuación\ ref {9.8} es clave para entender el comportamiento de los inductores. Como se señaló anteriormente, si un inductor es accionado por una fuente de voltaje fijo e ignorando\(R_{coil}\), la corriente a través de él se eleva a la tasa constante de\(\mathcal{v}/L\). Este cambio en la corriente a través del inductor no es ilimitado. Un cambio instantáneo requiere que\(di/dt\) sea infinito, y así, el voltaje que acciona el inductor también tendría que ser infinito, lo cual es una clara imposibilidad. Por lo tanto, podemos afirmar una característica particularmente importante de los capacitores:

\[\text{The current through an inductor cannot change instantaneously.} \label{9.10} \]

Esta observación será central para analizar el funcionamiento de inductores en circuitos de CC.

Referencias

¹ Verdaderamente uno de los inventos más geniales de todos los tiempos: un imán con un interruptor de encendido/apagado.

² El alambre enrollado debe estar aislado, de lo contrario cada bucle se cortará con los bucles próximos a él y nos quedaríamos con un tubo en lugar de una serie de bucles.