3.15: Introducción a las Radios Definidas por Software

Los esquemas de radio celular 2G y 3G utilizaron muy pocos métodos de modulación. Con la introducción de 4G y ahora 5G muchos métodos de modulación deben ser soportados con el esquema de modulación de orden más alto utilizado determinado por el nivel de ruido e interferencia en un canal. Este soporte para múltiples métodos de modulación solo es posible si la mayor parte del proceso de demodulación se realiza en DSP donde el software controla la demodulación. Tal radio se llama radio definida por software (SDR). En un SDR muchas de las funciones que tradicionalmente se realizarían usando hardware analógico se implementan digitalmente y solo las funciones de RF cercanas a la antena de transmisión/recepción se implementan en forma analógica. Un concepto extremo para el lado transmisor de la radio es implementar todas las funciones digitalmente con un convertidor digital a analógico (DAC) final conectado a una antena. Entonces el rendimiento está limitado por la frecuencia máxima y la potencia de salida del DAC. Este último SDR proporciona la máxima flexibilidad, por ejemplo, es fácil cambiar los esquemas de modulación, pero también contribuiría a un consumo muy alto de la batería. Entonces, en cambio, hay una compensación con muchos aspectos como la modulación y la sintonización fina de la frecuencia portadora de RF realizada digitalmente mientras que, con un transmisor, la conversión ascendente final se realiza usando hardware analógico que solo necesita ser capaz de soportar el ancho de banda de la señal modulada pero por lo demás es agnóstico a el tipo de modulación utilizada.

Todas las radios utilizan hoy en día la modulación en cuadratura, un tipo de modulación digital, en la que los componentes reales (en fase) e imaginarios (cuadratura-fase) del fasor de la portadora se varían independientemente. Si bien es posible variar la amplitud y fase de un tono portador por separado esto no es común.

La demodulación en cuadratura recupera las señales originales que variaron los componentes en fase y cuadratura de fase de la portadora. La demodulación puede proceder por etapas con una separación analógica inicial de señales RF en fase y cuadratura que son muestreadas por un convertidor analógico-digital (ADC) y demodulación completada en un procesador de señal digital.

En las siguientes secciones se discuten diversos aspectos de una radio SDR. La Sección 3.9 comienza con una descripción de la modulación en cuadratura de una manera que ayuda en la comprensión de un transmisor SDR. En la Sección 3.10 se presenta un ejemplo específico de un transmisor SDR en el que se siguen las señales de dominio de tiempo y dominio de frecuencia a través de primero un procesador de señal digital (DSP) y luego un convertidor ascendente analógico para producir una señal de RF. A esta discusión le sigue una descripción de un receptor SDR con el demodulador general en cuadratura SDR en la Sección 3.11 y luego un ejemplo específico en la Sección 3.12.

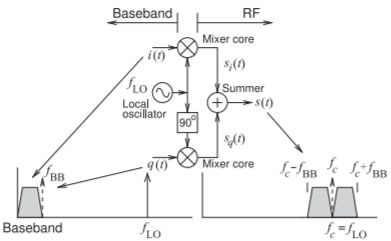
Figura\(\PageIndex{1}\): Modulación de portadora suprimida de doble banda lateral (DSB-SC). Modulador en cuadratura con señales de banda base moduladoras independientes\(i(t)\), la entrada del componente en fase al núcleo del mezclador en fase y\(q(t)\) el componente en cuadratura que impulsa el núcleo del mezclador en cuadratura de fase. Esto da como resultado una señal modulada con dos bandas laterales alrededor del oscilador local o frecuencia portadora. Cada banda lateral RF tiene una mezcla de la información en\(i(t)\) y\(q(t)\).