8.1: Estimación
- Page ID
- 82524
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
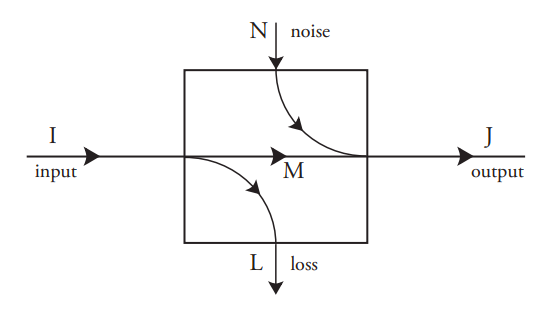
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A menudo es necesario determinar el evento de entrada cuando solo se ha observado el evento de salida. Este es el caso de los sistemas de comunicación, en los que el objetivo es inferir el símbolo emitido por la fuente para que pueda reproducirse en la salida. También es el caso de los sistemas de memoria, en los que el objetivo es recrear el patrón de bits original sin error.
En principio, esta estimación es sencilla si se conocen la distribución de probabilidad de entrada\(p(A_i)\) y las probabilidades de salida condicionales, condicionadas a los eventos de entrada.\(p(B_j \;|\; A_i) = c_{ji}\) Estas probabilidades condicionales “hacia adelante”\(c_{ji}\) forman una matriz con tantas filas como eventos de salida, y tantas columnas como eventos de entrada haya. Son propiedad del proceso, y no dependen de las probabilidades de entrada\(p(A_i)\).
La probabilidad incondicional\(p(B_j)\) de cada evento de salida\(B_j\) es
\(p(B_j) = \displaystyle \sum_{i} c_{ji}p(A_i)\tag{8.1}\)
y la probabilidad conjunta de cada entrada con cada salida\(p(A_i, B_j)\) y las probabilidades condicionales hacia atrás se\(p(A_i \;|\; B_j)\) pueden encontrar usando el Teorema de Bayes:
\ begin {alinear*}
p (A_ {i}, B_ {j}) &=p (B_ {j}) p (A_ {i}\; |\; B_ {j})\\
&= p (A_ {i}) p (B_ {j}\; |\; A_ {i})\ tag {8.2}\\
&=p (A_ {i}) c_ {ji}
\ final {alinear*}
Ahora supongamos que se\(B_j\) ha observado un evento de salida particular. El evento de entrada que “causó” esta salida puede estimarse solo en la medida de dar una distribución de probabilidad sobre los eventos de entrada. Para cada evento de entrada\(A_i\) la probabilidad de que fuera la entrada es simplemente la probabilidad condicional hacia atrás\(p(A_i \;|\; B_j)\) para el evento de salida particular\(B_j\), que se puede escribir usando la Ecuación 8.2 como
\(p(A_i \;|\; B_j) = \dfrac{p(A_i)c_{ji}}{p(B_j)} \tag{8.3}\)
Si el proceso no tiene pérdida (\(L\)= 0) entonces para cada uno\(j\) exactamente uno de los eventos de entrada\(A_i\) tiene una probabilidad distinta de cero, y por lo tanto su probabilidad\(p(A_i \;|\; B_j)\) es 1. En el caso más general, con pérdidas distintas de cero, la estimación consiste en refinar un conjunto de probabilidades de entrada para que sean consistentes con la salida conocida. Tenga en cuenta que este enfoque solo funciona si se conoce la distribución de probabilidad de entrada original. Todo lo que hace es afinar esa distribución a la luz de nuevos conocimientos, es decir, la producción observada.
Podría pensarse que la nueva distribución de probabilidad de entrada tendría menos incertidumbre que la de la distribución original. ¿Es esto siempre cierto?
La incertidumbre de una distribución de probabilidad es, por supuesto, su entropía como se definió anteriormente. La incertidumbre (sobre el evento de entrada) antes de que se conozca el evento de salida es
\(U_{\text{before}} = \displaystyle \sum_{i} p(A_i) \log_2 \Big(\dfrac{1}{p(A_i)}\Big) \tag{8.4}\)
La incertidumbre residual, después de que se conoce algún evento de salida particular, es
\(U_{\text{after}}(B_j) = \displaystyle \sum_{i} p(A_i \;|\; B_j) \log_2 \Big(\dfrac{1}{p(A_i \;|\; B_j)}\Big) \tag{8.5}\)
La pregunta, entonces es si\(U_{\text{after}}(B_j) ≤ U_{\text{before}}\). La respuesta suele ser, pero no siempre, sí. Sin embargo, no es difícil probar que el promedio (sobre todos los estados de producción) de la incertidumbre residual es menor que la incertidumbre original:
\(\displaystyle \sum_{j} p(B_j)U_{\text{after}}(B_j) ≤ U_{\text{before}} \tag{8.6}\)
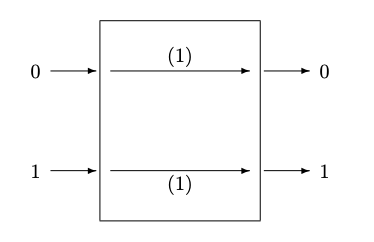
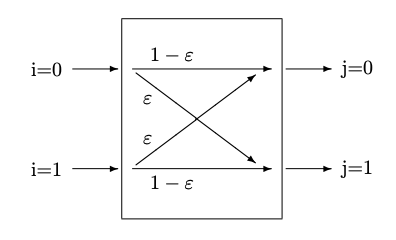
Figura 8.2:: (a) Canal binario sin ruido (b) Canal binario simétrico, con errores
En palabras, esta afirmación dice que en promedio, nuestra incertidumbre sobre el estado de entrada nunca se incrementa al aprender algo sobre el estado de salida. Es decir, en promedio, esta técnica de inferencia nos ayuda a obtener una mejor estimación del estado de entrada.
Dos de los siguientes ejemplos continuarán en capítulos posteriores, incluido el siguiente capítulo sobre el Principio de máxima entropía: el canal binario simétrico y Berger's Burgers.

