3.5: Problemas

Ejercicio\(\PageIndex{1}\) Airfoils

1. En un experimento de túnel de viento se ha medido la distribución de presiones sobre un perfil aerodinámico simétrico para un ángulo de ataque de\(14^{\circ}\). La distribución del coeficiente de presiones en los intrados\(C_{pl}\), y extrados\(C_{pE}\), del perfil aerodinámico puede aproximarse respectivamente mediante las siguientes funciones:
   \[C_{pl} (x) = \begin{cases} 1 - 2 \tfrac{x}{c}, \ \ \ \ \ \ & 0 \le x \le \tfrac{c}{4}, \\ \tfrac{2}{3} (1 - \tfrac{x}{c} ) \ \ \ \ \ \ & \tfrac{c}{4} \le x \le c; \end{cases}\nonumber\]
   \[C_{pE} (x) = \begin{cases} - 12 \tfrac{x}{c}, \ \ \ \ \ \ & 0 \le x \le \tfrac{c}{4}, \\ 4 (-1 + \tfrac{x}{c} ) \ \ \ \ \ \ & \tfrac{c}{4} \le x \le c. \end{cases}\nonumber\]
   (a) Dibujar la curva que representa la distribución de presiones.
   (b) Considerando una cuerda\(c = 1\) m, obtener el coeficiente de sustentación del perfil aerodinámico.
   (c) Calcular la pendiente de la curva característica\(c_l (\alpha)\).
2. Con base en una superficie aerodinámica como la sección transversal, construimos un ala rectangular con una envergadura de\(b = 20\) m y cuerda constante\(c = 1\) m. La distribución del coeficiente de sustentación a lo largo de la envergadura del ala (\(y\)eje) para un ángulo de ataque\(\alpha = 14^{\circ}\) se aproxima por la siguiente parabólica function:
   \[c_l (y) = 1.25 - 5 (\dfrac{y}{b})^2, - \dfrac{b}{2} \le y \le \dfrac{b}{2}.\nonumber\]
   (a) Dibujar la curva\(c_l (y)\).
   (b) Calcular el coeficiente de sustentación del ala.

Responder

1. 
   a) La curva es la siguiente:
   
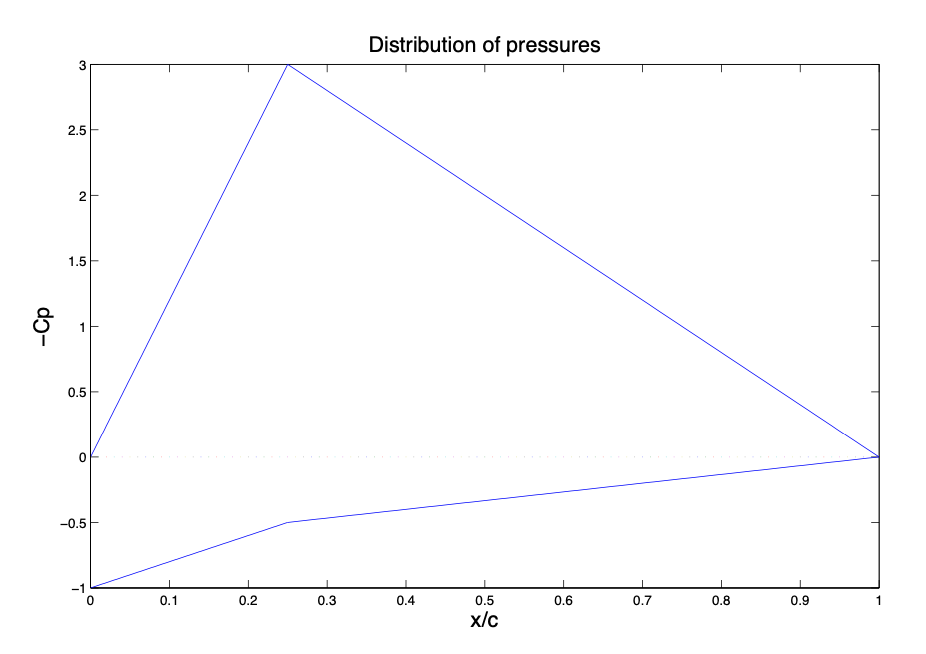
   Figura 3.28: Distribución del coeficiente de presiones.
   b) El coeficiente de sustentación para el perfil aerodinámico para se\(\alpha = 14^{\circ}\) puede calcular de la siguiente manera:
   \[c_l = \dfrac{1}{c} \int_{x_{le}}^{x_{te}} (c_{pl} (x) - c_{pE} (x)) dx,\label{eq3.5.1}\]
   En este caso, con\(c = 1\) y las distribuciones dadas de presiones de Intrados y extrados, la Ecuación (\(\ref{eq3.5.1}\)) se convierte en:
   \[c_l = \dfrac{1}{c} \left [ \int_{0}^{1/4} ((1 - 2x) - (-12x)) dx + \int_{1/4}^{1} (2/3 (1 - x) - 4(-1 + x)) dx \right ] = 1.875. \nonumber\]
   (c) La curva característica viene dada por:
   \[c_l = c_{l_0} + c_{l_{\alpha}} \alpha.\nonumber\]
   Dado que el perfil aerodinámico es simétrico:\(c_{l_0} = 0\). Por lo tanto\(c_{l_{\alpha}} = \tfrac{c_l}{\alpha} = \tfrac{1.875 \cdot 360}{14 \cdot 2\pi} = 7.16 \ 1/rad\).
2. 
   (a) La curva es la siguiente:
   
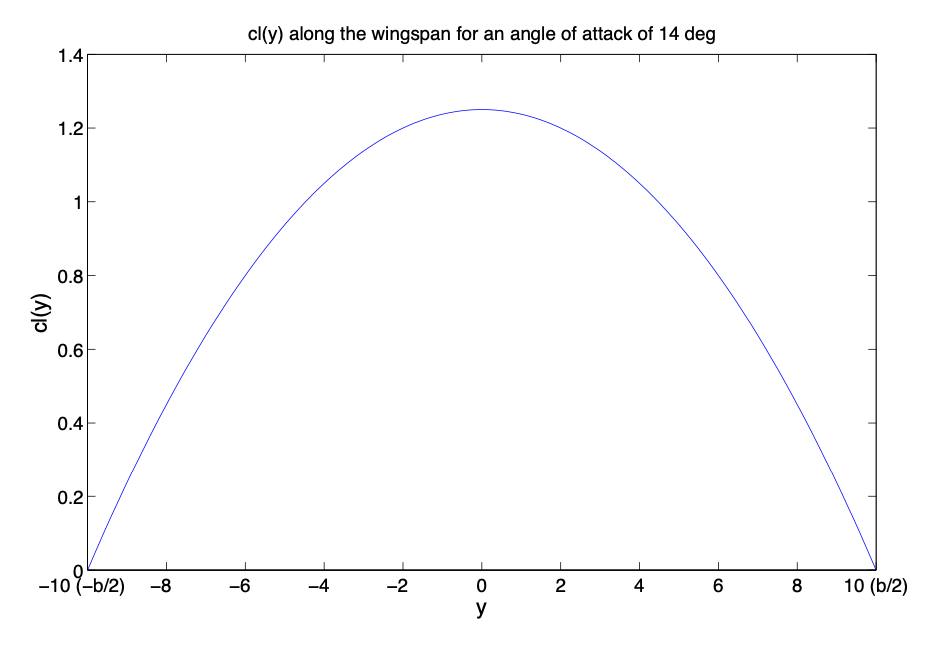
   Figura 3.29: Coeficiente de elevación a lo largo de la envergadura.
   (b) El coeficiente de sustentación para el ala se\(\alpha = 14^{\circ}\) puede calcular de la siguiente manera:
   \[C_L = \dfrac{1}{S_w} \int_{-b/2}^{b/2} c(y) c_l (y) dy.\label{eq3.5.2}\]
   Sustituyendo en la Ecuación (\(\ref{eq3.5.2}\)) considerando\(c(y) = 1\) y\(b = 20\):
   \[C_L = \dfrac{1}{20} \int_{-10}^{10} \left (1.25 - 5 (\dfrac{y}{20})^2 \right ) dy = 0.83.\nonumber\]

Ejercicio\(\PageIndex{2}\) Airfoils

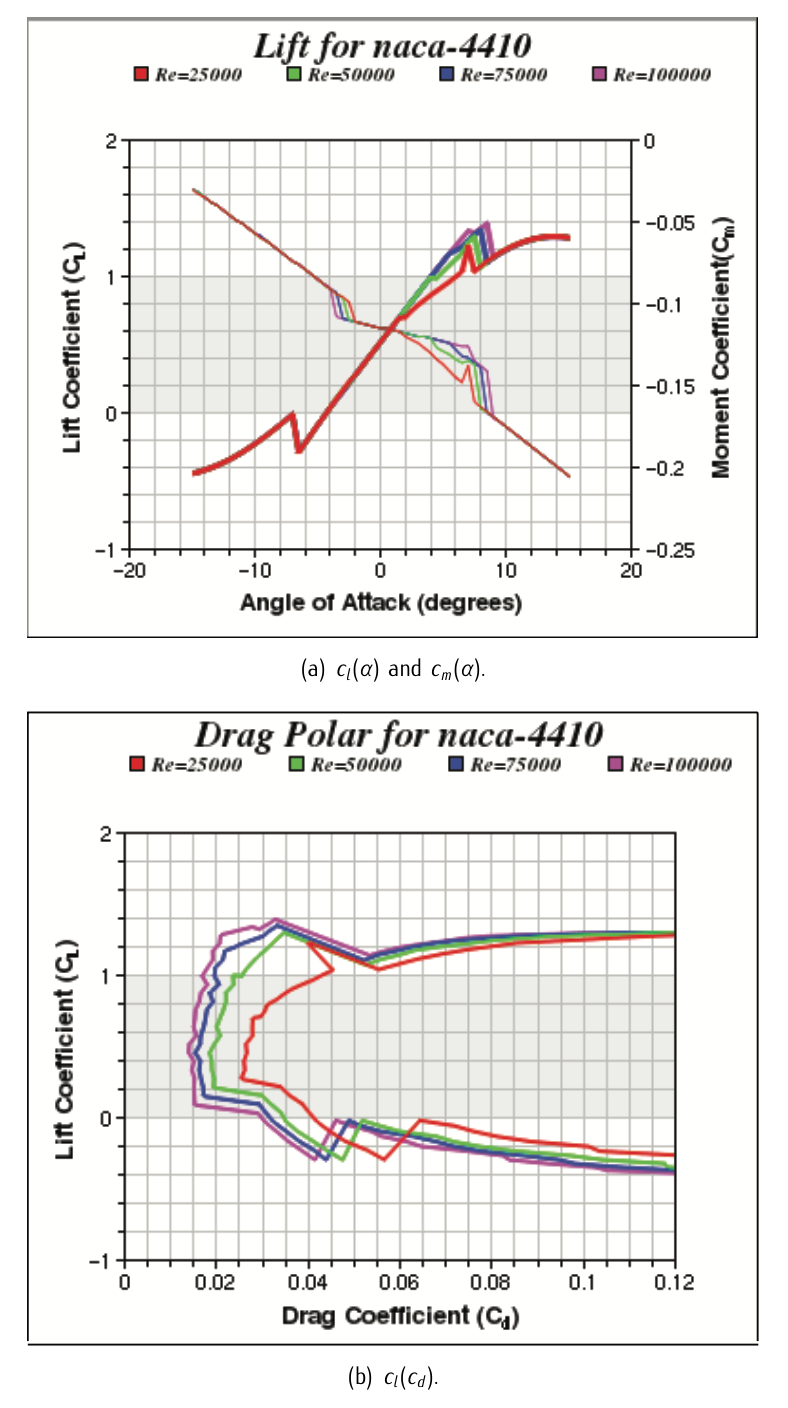
Figura 3.30: Curvas características de un perfil aerodinámico NACA 4410.

Queremos conocer las características aerodinámicas de un perfil aerodinámico NACA-4410 para un número Reynolds\(\text{Re} = 100000\). Los resultados experimentales dieron las curvas características mostradas en la Figura 3.30.

Calcular:

1. La expresión de la curva de elevación en el rango lineal en la forma:\(c_l = c_{l0} + c_{l\alpha} \alpha\).
2. La expresión del polar parabólico del perfil aerodinámico en la forma:\(c_d = c_{d0} + b_{c_l} + kc_l^2.\)
3. el ángulo de ataque y el coeficiente de sustentación correspondiente al coeficiente mínimo de arrastre.
4. El ángulo de ataque, el coeficiente de sustentación y el coeficiente de arrastre correspondientes a la máxima eficiencia aerodinámica.
5. Los valores de las fuerzas aerodinámicas por unidad de longitud que el modelo con cuerda\(c= 2\) m produciría en los experimentos de túnel de viento con ángulo de ataque\(\alpha = 3^{\circ}\) y corriente incidente con número de Mach\(M = 0.3\). Considera las condiciones ISA a una altitud de\(h = 1000\) m.

Responder

Queremos aproximar los datos experimentales dados en la Figura 3.30, respectivamente, a una línea recta y una curva parabólica. Por lo tanto, para definir unívocamente tales curvas, debemos elegir:

• Dos pares de puntos (\(c_l, \alpha\)) de la\(c_l (\alpha)\) curva en la Figura 3.30.a.
• Tres pares de puntos (\(c_l, c_d\)) de la\(c_l (c_d)\) curva en la Figura 3.30.b.

Según la Figura 3.30 Para\(\text{Re} = 100000\) nosotros elegimos (cualquier otra combinación elegida correctamente debe funcionar):

\(c_l\)	\(\alpha\)
0.5	\(0^{\circ}\)
1	\(4^{\circ}\)

Cuadro 3.3: Fecha obtenida de la Figura 3.30.a.

\(c_l\)	\(c_d\)
0	0.03
1	0.0175
1.4	0.0325

Cuadro 3.4: Datos obtenidos de la Figura 3.30.b.

1. La expresión de la curva de elevación en el rango lineal en la forma:\(c_l = c_{l0} + c_{l\alpha} \alpha\):
   Con los datos en la Tabla 3.3:
   \[c_{l0} = 0.5;\]
   \[c_{l\alpha} = 7.16 \cdot 1/rad.\]
   La curva requerida rinde entonces:
   \[c_l = 0.5 + 7.16 \alpha [\alpha \ in \ rad]\label{eq3.5.5}\]
2. La expresión del polar parabólico de la superficie aerodinámica en la forma:\(c_d = c_{d0} + bc_l + kc_l^2\):
   Con los datos en la Tabla 3.4 tenemos un sistema de tres ecuaciones con tres unkowns que está por resolver. Rende:
   \[c_{d0} = 0.03;\]
   \[b = -0.048;\]
   \[k = 0.0357.\]
   La expresión de los rendimientos polares parabólicos:
   \[c_d = 0.03 - 0.048 c_l + 0.0357 c_l^2.\label{eq3.5.9}\]
3. El ángulo de ataque y el coeficiente de sustentación correspondiente al coeficiente mínimo de arrastre:
   Para ello, buscamos el mínimo de la curva parabólica:
   \[\dfrac{dc_l}{dc_d} = 0 = b + 2 \cdot kc_l.\]
   Sustituyendo en la Ecuación (\(\ref{eq3.5.9}\)):
   \[\dfrac{dc_l}{dc_d} = 0 = -0.048 + 2 \cdot 0.0357 c_l \to (c_l)_{c_{d_{\min}}} = 0.672.\]
   Sustituyendo\((c_l)_{c_{d_{\min}}}\) en la Ecuación (\(\ref{eq3.5.5}\)), obtenemos:
   \[(\alpha)_{c_{d_{\min}}} = 0.024\ rad (1.378^{\circ}).\nonumber\]
4. El ángulo de ataque, el coeficiente de sustentación y el coeficiente de arrastre correspondientes a la máxima eficiencia aerodinámica:
   La eficiencia aerodinámica se define como:
   \[E = \dfrac{l}{d} = \dfrac{c_l}{c_d}.\label{eq3.5.12}\]
   Sustituyendo la curva polar parabólica en la Ecuación (\(\ref{eq3.5.12}\)), obtenemos:
   \[E = \dfrac{c_l}{c_{d0} + bc_l + kc_l^2}.\]
   Para buscar los valores correspondientes a la máxima eficiencia aerodinámica, se debe derivar y hacerla igual a cero, es decir:
   \[\dfrac{dE}{dc_l} = 0 = \dfrac{c_{d0} - kc_l^2}{(c_{d0} + bc_l + kc_l^2)^2} \to (c_l)_{E_{\max}} = \sqrt{\dfrac{c_{d0}}{k}}.\]
   Sustituir según los valores previamente obtenido (\(c_{d0} = 0.03, k = 0.0357\)):\((c_l)_{E_{\max}} = 0.91\). Sustituyendo en la Ecuación (\(\ref{eq3.5.5}\)) y la Ecuación (\(\ref{eq3.5.9}\)), obtenemos:
   \(\bullet (\alpha)_{E_{\max}} = 0.058\ rad\ (3.33^{\circ});\)
   \(\bullet (c_d)_{E_{\max}} = 0.01588.\)
5. Los valores de las fuerzas aerodinámicas por unidad de longitud que el modelo con cuerda\(c = 2\) m produciría en los experimentos de túnel de viento con ángulo de ataque\(\alpha = 3^{\circ}\) y corriente incidente con número Mach\(M = 0.3\):
   Según ISA:
   \(\bullet \rho (h = 1000) = 0.907\ kg/m^3\);
   \(\bullet a(h = 1000) = \sqrt{\gamma_{air} R (T_0 - \lambda h)} = 336.4\ m/s\);
   donde a corresponde a la velocidad del sonido,\(\gamma_{air} = 1.4, R = 287\ J/KgK, T_0 = 288.15\ k\) y\(\lambda = 6.5 \cdot 10^{-3}\).
   Dado que el experimento está destinado a ser en\(M = 0.3\):
   \[V = M \cdot a = 100.92\ m/s.\]
   Dado que el experimento está destinado a estar en\(\alpha = 3^{\circ}\), usando la Ecuación (\(\ref{eq3.5.5}\)) y la Ecuación (\(\ref{eq3.5.9}\)):
   \[c_l = 0.87;\]
   \[c_d = 0.01526.\]
   Finalmente:
   \[l = c_l \dfrac{1}{2} \rho c V^2 = 8036.77\ N/m;\]
   \[d = c_d \dfrac{1}{2} \rho c V^2 = 140.96\ N/m.\]

Ejercicio\(\PageIndex{3}\) Wings

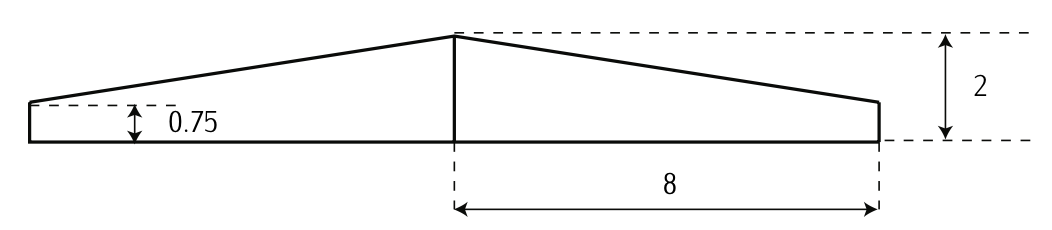
Figura 3.31: Forma de planta del ala (Dimensiones en metros)

Queremos analizar los rendimientos aerodinámicos de un ala trapezoidal con forma de planta como en la Figura 3.31 y un factor de eficiencia del ala de\(e = 0.96\). Además, emplearemos un perfil aerodinámico NACA 4415 con las siguientes características:

• \(c_l = 0.2 + 5.92 \alpha\).
• \(c_d = 6.4 \cdot 10^{-3} - 1.2 \cdot 10^{-3} c_l + 3.5 \cdot 10^{-3} c_l^2\).

Calcular:

1. Los siguientes parámetros del ala ⁴: cuerda en la raíz; cuerda en la punta; cuerda media; superficie húmeda ala-spanl; agrandamiento.
2. La curva de sustentación del ala en el rango lineal.
3. El polar del ala asumiendo que se puede calcular como\(C_D = C_{D_0} + C_{D_i} C_L^2\).
4. Calcular el coeficiente óptimo de sustentación\(C_{L_{opt}}\),, para el ala. Compárela con la del perfil aerodinámico.
5. Calcular el coeficiente óptimo de arrastre,\(C_{D_{opt}}\), para el ala. Compárela con la del perfil aerodinámico.
6. Máxima eficiencia aerodinámica,\(E_{\max}\), para el ala. Compárela con la del perfil aerodinámico.
7. Discutir las diferencias observadas en\(C_{L_{opt}}\)\(C_{D_{opt}}\), y\(E_{\max}\) entre el ala y el perfil aerodinámico.

Responder

1. Acorde en la raíz; cuerda en la punta; cuerda media; tramo de ala; superficie húmeda; agrandamiento:

Según la Figura 3.31:

El tramo de ala,\(b\), es\(b = 16\ m\). El acorde a la ip,\(c_t\), es\(c_t = 0.75\ m\). El acorde en la raíz,\(c_r\), es\(c_r = 2\ m\).

\[C_l = C_{l_0} + C_{l_{\alpha}} \alpha.\]

Por lo tanto, con la Ecuación (3.67) y la Ecuación (3.68) en la Ecuación (3.69), tenemos que:

También podemos calcular la superficie húmeda del ala calculando el doble del área de un tropezoide de la siguiente manera:

\[S_w = 2 \left (\dfrac{(c_r + c_t)}{2} \dfrac{b}{2} \right ) = 22\ m^2.\nonumber\]

El acorde medio,\(\bar{c}\), se puede calcular como\(\bar{c} = \tfrac{S_w}{b} = 1.375\ m\); y la ampliación,\(A\), como\(A = \tfrac{b}{\bar{c}} = 11.63\).

2. Curva de elevación del ala:

La curva de sustentación de un ala se puede expresar de la siguiente manera:

\[C_L = C_{L_0} + C_{L_{\alpha}} \alpha,\label{eq3.5.21}\]

y la pendiente de la curva de sustentación del ala se puede expresar relacionada con la pendiente de la curva de sustentación del ala como:

\[C_{L_{\alpha}} = \dfrac{C_{l_{\alpha}}}{1 + \tfrac{C_{t_{\alpha}}}{\pi A}} e = 4.89 \cdot 1/rad.\nonumber\]

Para calcular el término independiente de la curva de sustentación del ala, debemos considerar el hecho de que el ángulo de ataque de levantamiento cero del ala coincide con el ángulo de ataque de cero sustentación del ala, es decir:

\[\alpha (L = 0) = \alpha (l = 0).\label{eq3.5.22}\]

Primero, observe que la curva de sustentación de un perfil aerodinámico se puede expresar de la siguiente manera

\[C_l = C_{l_0} + C_{l_{\alpha}} \alpha.\label{eq3.5.23}\]

Por lo tanto, con la Ecuación (\(\ref{eq3.5.21}\)) y la Ecuación (\(\ref{eq3.5.22}\)) en la Ecuación (\(\ref{eq3.5.23}\)), tenemos que:

\[C_{L_0} = C_{l_0} \dfrac{C_{L_{\alpha}}}{C_{l_{\alpha}}} = 0.165.\nonumber\]

La curva requerida rinde entonces:

\[C_L = 0.165 + 4.89 \alpha [\alpha \ in \ rad].\nonumber\]

3. La expresión del polar parabólico del ala:

Observe primero que la afirmación del problema indica que el polar debe estar en la siguiente forma:

\[C_D = C_{D0} + C_{D_i} C_L^2.\label{eq3.5.24}\]

Para el cálculo de la resistencia parabólica del ala podemos considerar el término parásito aproximadamente igual al término parásito del perfil aerodinámico, es decir,\(C_{D_0} = C_{d_0}\).

\ (C_ {D_i} =\ dfrac {1} {\ pi Ae} = 0.028. \ nonumber\]

La expresión de los rendimientos polares parabólicos entonces:

\[C_D = 0.0064 + 0.028 C_L^2.\label{eq3.5.25}\]

4. El coeficiente óptimo de sustentación,\(C_{L_{opt}}\), para el ala. Compárela con la del perfil aerodinámico.

El coeficiente óptimo de sustentación es el que hace que la eficiencia aerodinámica sea máxima. La eficiencia aerodinámica se define como:

\[E = \dfrac{L}{D} = \dfrac{C_L}{C_D}.\label{eq3.5.26}\]

Sustituyendo el polar parabólico dado en la Ecuación (\(\ref{eq3.5.24}\)) en la Ecuación (\(\ref{eq3.5.26}\)), obtenemos:

\[E = \dfrac{C_L}{C_{D_0} + C_{D_i} C_L^2}.\]

Para buscar los valores correspondientes a la máxima eficiencia aerodinámica, se debe derivar y hacerla igual a cero, es decir:

\[\dfrac{dE}{dC_L} = 0 = \dfrac{C_{D_0} - C_{D_i} C_L^2}{(C_{D_0} + C_{D_i} C_L^2)^2} \to (C_L)_{E_{\max}} = C_{L_{opt}} = \sqrt{\dfrac{C_{D_0}}{C_{D_i}}}.\label{eq3.5.28}\]

Para el caso de un perfil aerodinámico, la eficiencia aerodinámica se define como:

\[E = \dfrac{1}{d} = \dfrac{c_l}{c_d}.\label{eq3.5.29}\]

Sustituyendo la curva polar parabólica dada en el enunciado en la forma\(c_{d_0} + bc_l + kc_l^2\) en la Ecuación (\(\ref{eq3.5.29}\)), obtenemos:

\[E = \dfrac{c_l}{c_{d_0} + bc_l + kc_l^2}.\]

Para buscar los valores correspondientes a la máxima eficiencia aerodinámica, se debe derivar y hacerla igual a cero, es decir:

\[\dfrac{dE}{dC_l} = 0 = \dfrac{c_{d_0} - kc_l^2}{(c_{d0} + bc_l + kc_l^2)^2} \to (C_l)_{E_{\max}} = (c_l)_{opt} = \sqrt{\dfrac{c_{d_0}}{k}}.\label{eq3.5.31}\]

De acuerdo con los valores previamente obtenidos (\(C_{D_0} = 0.0064\)y\(C_{D_i} = 0.028\)) y los valores dados en el enunciado para el polar (\(c_{d_0} = 0.0064\),\(k = 0.0035\)) del perfil aerodinámico, sustituyéndolos en la Ecuación (\(\ref{eq3.5.28}\)) y Ecuación (\(\ref{eq3.5.31}\)), respectivamente, obtenemos:

• \((C_L)_{opt} = 0.478;\)
• \((c_l)_{opt} = 1.35.\)

5. El coeficiente óptimo de arrastre,\(C_{D_{opt}}\) para el ala. Compárelo con el de los perfiles aerodinámicos:

Una vez obtenido el coeficiente óptimo de sustentación tanto para el ala como para el ala, simplemente sustituyendo sus valores en ambas curvas parabólicas dadas respectivamente en el enunciado y en la Ecuación (\(\ref{eq3.5.25}\)), obtenemos:

\[C_{D_{opt}} = 0.0064 + 0.028 C_{l_{opt}}^2 = 0.01279.\nonumber\]

\[c_{d_{opt}} = 6.4 \cdot 10^{-3} - 1.2 \cdot 10^{-3} c_{l_{opt}} + 3.5 \cdot 10^{-3} c_{l_{opt}}^2 = 0.01115.\nonumber\]

6. Máxima eficiencia aerodinámica\(E_{\max}\) para el ala. Compárelo el de los perfiles aerodinámicos:

La máxima eficiencia aerodinámica se puede obtener como:

\[E_{\max_{wing}} = \dfrac{C_{L_{opt}}}{C_{D_{opt}}} = 37.\nonumber\]

\[E_{\max_{airfoil}} = \dfrac{c_{l_{opt}}}{c_{d_{opt}}} = 121.\nonumber\]

7. Discutir las diferencias\(C_{L_{opt}}\) observadas en\(C_{D_{opt}}\) y\(E_{\max}\) entre el ala y el perfil aerodinámico.

De acuerdo con los resultados es sencillo ver que mientras tanto el coeficiente óptimo de arrastre es similar tanto para el ala como para el ala, el coeficiente óptimo de sustentación es aproximadamente tres veces menor que el del perfil aerodinámico. Obviamente esto resulta en una eficiencia aproximadamente tres veces menor para el ala en comparación con la del ala.

¿Qué significa? Un avión tridimensional hecho de perfil\(2D\) aerodinámico genera mucha más resistencia que el\(2D\) perfil aerodinámico para lograr una elevación requerida. Por lo tanto, no podemos simplemente extrapolar el análisis de un perfil aerodinámico al ala.

Dicha pérdida de eficiencia se debe al llamado arrastre inducido por sustentación. La explicación detrás de este comportamiento se debe a la diferencia de presiones entre extrados e intrados. En particular, en la región cercana al borde marginal, existe una corriente de aire que rodea el borde marginal que pasa de los intrados, donde la presión es mayor, a extrados, donde la presión es menor, dando lugar a dos vórtices, uno en cada borde girando en sentido horario y antihorario. Este fenómeno produce aguas abajo un sendero torbellino.

La presencia de este rastro modifica el fluido archivado y, en particular, modifica la velocidad que cada ala “ve”. Además de la velocidad de transmisión libre\(u_{\infty}\), se debe agregar una velocidad inducida vertical ui (Ver Figura 3.23). Cuanto más cerca del borde marginal, mayor es la velocidad inducida. Por lo tanto, el ángulo efectivo de ataque del perfil aerodinámico es menor que el ángulo geométrico, lo que explica tanto la reducción en el coeficiente de sustentación (con respecto al coeficiente bidimensional) como la aparición de y arrastre inducido (Ver Figura 3.24).

Ejercicio\(\PageIndex{4}\) Airfoils and Wings

1. En un experimento de túnel de viento hemos medido la distribución de presiones sobre un perfil aerodinámico simétrico con ángulo de ataque\(6^{\circ}\). Las distribuciones del coeficiente de presiones para intrados\((C_{pl})\) y extrados\((C_{pE})\) pueden aproximarse mediante las siguientes funciones: a
   \[C_{pl} (x) = \begin{cases} 10 \tfrac{x}{c}, \ \ \ \ \ \ \ & 0 \le \tfrac{x}{c} \le \tfrac{1}{10}, \\ 2 - 10 \tfrac{x}{c}, \ \ \ \ \ & \tfrac{1}{10} \le \tfrac{x}{c} \le \tfrac{1}{5}; \\ 0, \ \ \ \ \ \ & \tfrac{1}{5} \le \tfrac{x}{c} \le 1. \end{cases}\nonumber\]
   \[C_{pE} (x) = \begin{cases} -15 \tfrac{x}{c}, \ \ \ \ \ \ \ & 0 \le \tfrac{x}{c} \le \tfrac{1}{5}, \\ \tfrac{-15}{4} (1 - \tfrac{x}{c}, \ \ \ \ \ & \tfrac{1}{5} \le \tfrac{x}{c} \le 1. \end{cases}\nonumber\]
   ) Dibujar la curva\(-C_p (\tfrac{x}{c})\).
   b) Considerando\(c = 1 [m]\), calcular el coeficiente de sustentación del perfil aerodinámico.
2. Basándonos en el perfil aerodinámico anterior como sección transversal, queremos diseñar un ala rectangular con ala-span\(b\) y cuerda constante\(c = 1\ m\). La distribución del coeficiente de sustentación a lo largo del tramo del ala para el ángulo de ataque\(6^{\circ}\) puede aproximarse mediante la siguiente función:
   \[c_l (y) = c_{l_{airfoil}} \cdot (1 - \dfrac{4}{A} \cdot (\dfrac{y}{b})^2), -\dfrac{b}{2} \le y \le \dfrac{b}{2},\nonumber\]
   siendo\(c_{l_{airfoil}}\) el coeficiente de sustentación del perfil aerodinámico previamente calculado y A el agrandamiento del ala.
   a) Calcular el coeficiente de sustentación del ala en función de la ampliación\(A\).
   (b) Calcular el coeficiente de sustentación del ala para\(A = 1\),\(A = 8yA =\infty\).
   c) Dibujar la distribución del coeficiente de elevación a lo largo del tramo del ala para\(A = 1, A = 8yA = \infty\). Discutir los resultados.

Responder

1. Superficie aerográfica:

a) La curva es la siguiente:

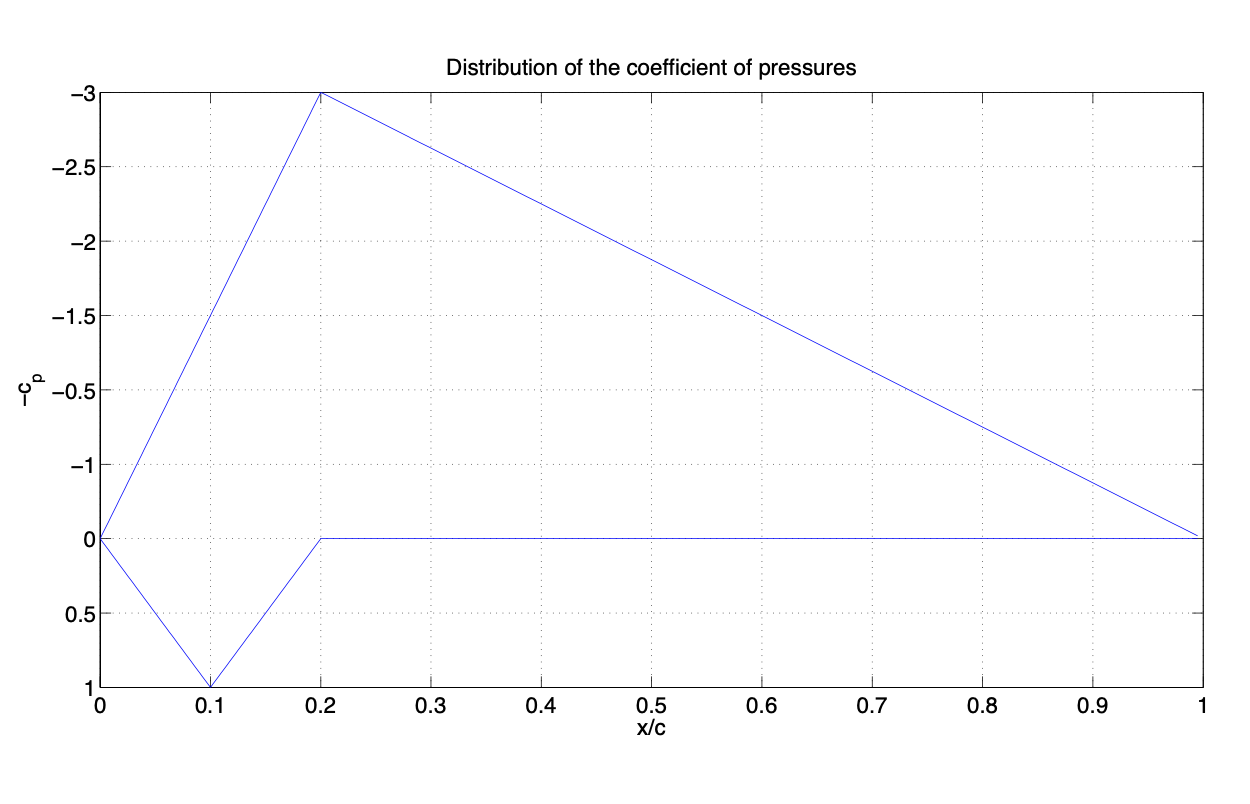
Figura 3.32: Distribución del coeficiente de presiones.

b) El coeficiente de sustentación del perfil aerodinámico para se\(\alpha = 6^{\circ}\) puede calcular de la siguiente manera:

\[c_l = \dfrac{1}{c} \int_{x_{le}}^{x_{te}} (c_{pl} (x) - c_{pE} (x)) dx.\label{eq3.5.32}\]

En este caso, con\(c = 1\) y las distribuciones dadas de presiones de intrados y extrados, la Ecuación (\(\ref{eq3.5.32}\)) se convierte en:

\[c_l = \dfrac{1}{c} \left [\int_{0}^{1/10} (10x) dx + \int_{1/10}^{1/5} (2 - 10x) dx + \int_{1/5}^{1} (0) dx - \int_{0}^{1/5} (-15x) dx - \int_{1/5}^{1} (-15/4 (1 - x)) dx \right ] = 1.6.\nonumber\]

2. Ala:

a) El coeficiente de sustentación para el ala\(\alpha = 6^{\circ}\) puede calcularse de la siguiente manera:

\[C_L = \dfrac{1}{S_w} \int_{-b/2}^{b/2} c(y) c_l (y) dy.\label{eq3.5.33}\]

Sustituyendo en la Ecuación (\(\ref{eq3.5.33}\)) considerando\(c(y) = 1\):

\[C_L = \dfrac{1}{b} \int_{-b/2}^{b/2} 1.6 \left (1 - \dfrac{4}{A} (\dfrac{y}{b})^2 \right ) dy = 1.6(1 - \dfrac{1}{3A}).\nonumber\]

b) Los valores de\(C_L\) para las diferentes ampliaciones son:

• \(A = 1 \to C_L = 1.06.\)
• \(A = 8 \to C_L = 1.53.\)
• \(A = \infty \to C_L = 1.6.\)

Considerando, por ejemplo, un tramo de ala\(b = 20\ m\), la curva es la siguiente:

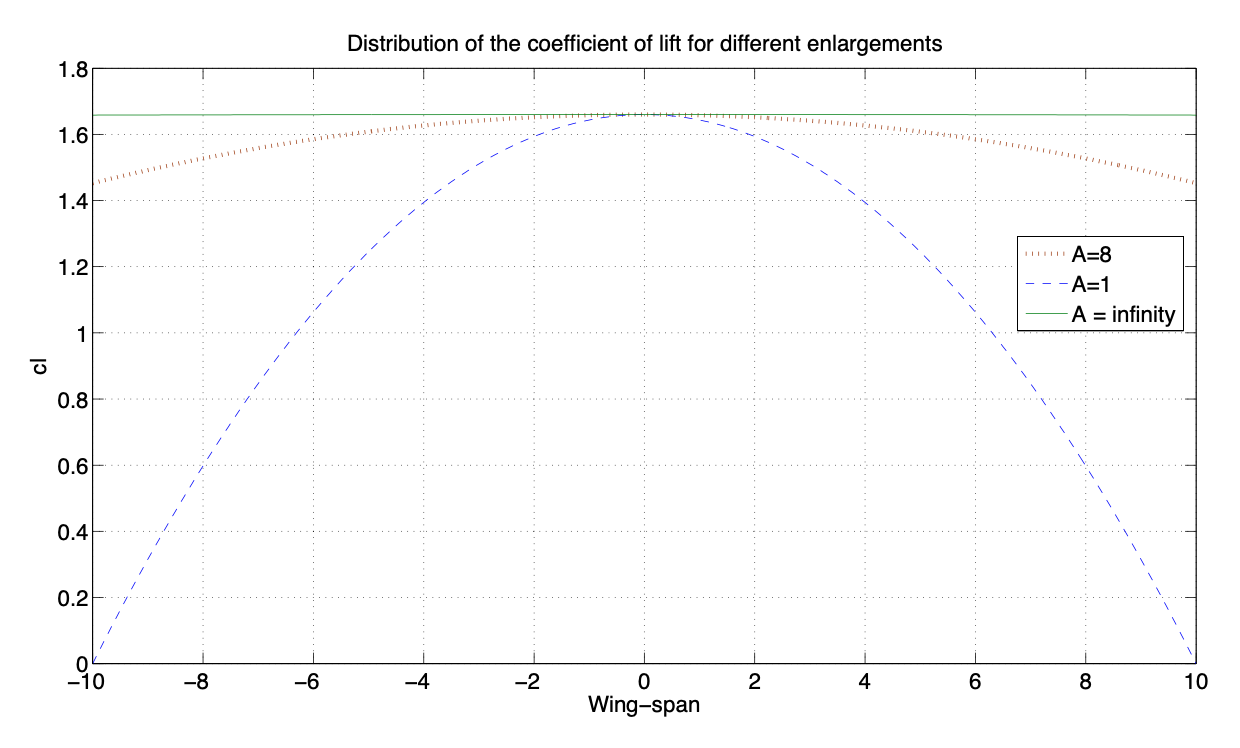
Figura 3.33: Coeficiente de elevación a lo largo de la envergadura

(c) La discusión tiene que ver con las diferencias en la generación de sustentación entre alas finitas y alas infinitas.

Se puede observar que si el agrandamiento es infinito el ala se comporta como la\(y (c_l(y)\) constante de superficie aerodinámica bidimensional). Por otro lado, si el agrandamiento es finito,\(c_l (y)\) muestra un máximo en la raíz del ala\((y = 0)\) y va a cero en la punta del ala\((y/c = A/2)\). A medida que disminuye el agrandamiento, el máximo\(c_l(y)\) también disminuye.

La explicación detrás de este comportamiento se debe a la diferencia de presiones entre extrados e intrados. En particular, en la región cercana al borde marginal, existe una corriente de aire que rodea el borde marginal que pasa de los intrados, donde la presión es mayor, a extrados, donde la presión es menor, dando lugar a dos vórtices, uno en cada borde girando en sentido horario y antihorario. Este fenómeno produce aguas abajo un sendero torbellino.

La presencia de este rastro modifica el campo fluido y, en particular, modifica la velocidad que cada ala “ve”. Además de la velocidad de transmisión libre\(u_{\infty}\), una velocidad inducida vertical,\(u_i\), debe agregarse (Ver Figura 3.23). Cuanto más cerca del borde marginal, mayor es la velocidad inducida. Por lo tanto, el ángulo efectivo de ataque del perfil aerodinámico es menor que el ángulo geométrico, lo que explica tanto la reducción en el coeficiente de sustentación (con respecto al coeficiente bidimensional) como el hecho de que esta reducción es mayor cuando uno se acerca al borde marginal.

Ejercicio\(\PageIndex{5}\) High-Lift devices

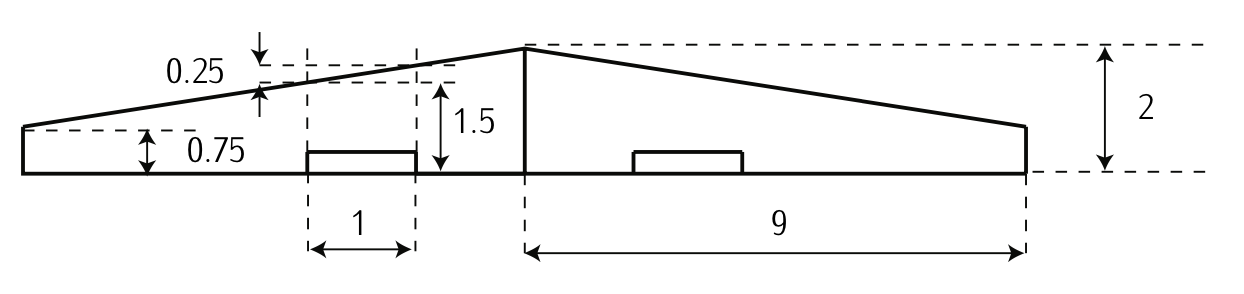
Figura 3.34: Forma de planta del ala (dimensiones en metros).

Queremos analizar los rendimientos aerodinámicos de un ala trapezoidal con forma de planta como en la Figura 3.34. El ala monta dos colgajos Fowler de triple ranura. El factor de eficiencia (factor Oswald) del ala es\(e = 0.96\). El ala se construye empleando\(NACA\) 4415 perfiles aerodinámicos con las siguientes características:

• \(c_l = 0.2 + 5.92 \alpha\). (\(\alpha\)en radianes)
• \(c_d = 6.4 \cdot 10^{-3} - 1.2 \cdot 10^{-3} c_l + 3.5 \cdot 10^{-3} c_l^2\).

En cuanto a los efectos de los colgajos Fowler en el coeficiente máximo de sustentación, se sabe que:

• El incremento del coeficiente máximo de sustentación del perfil aerodinámico (\(\Delta c_{l_{\max}}\)) se puede aproximar mediante la siguiente expresión:
  \[\Delta c_{l_{\max}} = 1.9 \dfrac{c'}{c},\label{eq3.5.34}\]
  ser\(c\) la cuerda en la raíz y\(c'\) la cuerda extendida (considerar\(c' = 3\ [m]\)).
• El incremento del coeficiente máximo de sustentación del ala (\(\Delta C_{L_{\max}}\)) puede estar relacionado con el incremento del coeficiente máximo de sustentación del perfil aerodinámico (\(\Delta c_{l_{\max}}\)) mediante la siguiente expresión:
  \[\Delta C_{L_{\max}} = 0.92 \Delta c_{l_{\max}} \dfrac{S_{fw}}{S_w} \cos \wedge.\label{eq3.5.35}\]

Con base en los datos dados en la Figura 3.34, calcular:

(a) Acorde en la raíz y punta del ala. envergadura del ala y agrandamiento. Superficie del ala mojada (\(S_w\)) y superficie mojada por los flaps (\(S_{fw}\)). Aviones barridos (\(\wedge\)) medidos desde el borde de ataque.

Suponiendo una configuración limpia (sin desviación del flap), típica de las condiciones de crucero, y sabiendo también que la parada del perfil aerodinámico tiene lugar en un ángulo de ataque de\(15^{\circ}\):

b) calcular el coeficiente máximo de sustentación del perfil aerodinámico.

(c) calcular la expresión de la curva de sustentación del ala en su rango lineal.

(d) calcular el coeficiente máximo de sustentación del ala (supongamos que la aeronave (ala) se para también en un ángulo de ataque de\(15^{\circ}\))

Suponiendo una configuración con flaps completamente desviados, típica de un enfoque final, calcule:

e) el coeficiente máximo de sustentación del ala.

Se sabe que la masa de la aeronave es\(4500\ kg\). Para\(ISA\) condiciones del nivel del mar y fuerza debida a la gravedad igual a\(9.81\ m/s^2\):

(f) calcular las velocidades de calado de la aeronave para ambas configuraciones (limpia y completa).

g) comparar y discutir los resultados.

Responder

a). Acorde en la raíz; cuerda en la punta; tramo de ala y agrandamiento; superficie húmeda del ala y superficie húmeda del colgajo; barrido:

Según la Figura 3.34:

• El tramo de ala,\(b\), es\(b = 18\ m\).
• El acorde en la punta,\(c_t\), es\(c_t = 0.75\ m\).
• El acorde en la raíz,\(c_r\), es\(c_r = 2\ m\).

También podemos calcular la superficie húmeda del ala calculando el doble del área de un trapecio de la siguiente manera:

\[S_w = 2 \left ( \dfrac{(c_r + c_t)}{2} \dfrac{b}{2} \right ) = 24.75\ m^2.\nonumber\]

De la misma manera, la superficie húmeda del colgajo se\((S_{fw})\) puede calcular de la siguiente manera:

\[S_{fw} = 2 \left ( 1 \cdot 1.5 + \dfrac{1}{2} 1 \cdot 0.25 \right ) = 3.25 \ m^2.\nonumber\]

El acorde medio,\(\bar{c}\), se puede calcular como\(\bar{c} = \tfrac{S_w}{b} = 1.375\ m\); y la ampliación,\(A\), como\(A = \tfrac{b}{\bar{c}} = 13.09\).

Finalmente, el barrido del ala (\(\wedge\)) medido desde el borde de ataque es:

\[\wedge = \arctan (\dfrac{0.25}{1}) = 14^{\circ}.\nonumber\]

b). \(c_{l_{\max}}\)

De acuerdo con la expresión dada en el enunciado para la curva de sustentación del perfil aerodinámico:\(c_l = 0.2 + 5.92 \alpha\), y dado que el perfil aerodinámico se estabiliza en\(\alpha = 15^{\circ}\), el coeficiente máximo de sustentación vendrá dado por el valor del coeficiente de sustentación en el ángulo de calado:

\[c_{l_{\max}} = 0.2 + 5.92 \cdot 15 \dfrac{2\pi}{360} = 1.74.\]

c). Curva de elevación del ala:

La curva de sustentación de un ala se puede expresar de la siguiente manera:

\[C_L = C_{L_0} + C_{L_{\alpha}} \alpha,\label{eq3.5.37}\]

y la pendiente de la curva de sustentación del ala se puede expresar relacionada con la pendiente de la curva de sustentación del ala como:

\[C_{L_{\alpha}} = \dfrac{C_{l_{\alpha}}}{1 + \tfrac{C_{l_{\alpha}}}{\pi A}} e = 4.96 \cdot 1/rad.\nonumber\]

Para calcular el término independiente de la curva de sustentación del ala, debemos considerar el hecho de que el ángulo de ataque de levantamiento cero del ala coincide con el ángulo de ataque de cero sustentación del ala, es decir:

\[\alpha (L = 0) = \alpha (l = 0).\label{eq3.5.38}\]

Primero, observe que la curva de sustentación de un perfil aerodinámico se puede expresar de la siguiente manera

\[C_l = C_{l_0} + C_{l_{\alpha}} \alpha.\label{eq3.5.39}\]

Por lo tanto, con la Ecuación (\(\ref{eq3.5.37}\)) y la Ecuación (\(\ref{eq3.5.38}\)) en la Ecuación (\(\ref{eq3.5.39}\)), tenemos que:

\[C_{L_0} = C_{l_0} \dfrac{C_{L_{\alpha}}}{C_{l_{\alpha}}} = 0.1678.\label{eq3.5.40}\]

La curva requerida rinde entonces:

\[C_L = 0.1678 + 4.96 \alpha \ [\alpha \ in \ rad].\nonumber\]

d). \(C_{L_{\max}}\)en configuración limpia:

Dada la expresión en la Ecuación (\(\ref{eq3.5.40}\)), y dado que la aeronave (ala) se para en\(\alpha = 15^{\circ}\), el coeficiente máximo de sustentación vendrá dado por:

\[C_{L_{\max}} = 0.1678 + 4.96 \cdot 15 \dfrac{2\pi}{360} = 1.466.\]

e). \(C_{L_{\max}}\)en configuración completa (con todas las aletas desviadas):

Para obtener el coeficiente máximo de elevación para la configuración completa\((C_{L_{\max}})\) tenemos que:

\[C_{L_{\max_f}} = C_{L_{\max}} + \Delta C_{L_{\max}}.\]

Como se dio en la Ecuación (\(\ref{eq3.5.35}\)), se\(\Delta C_{L_{\max}}\) puede expresar como:

\[\Delta C_{L_{\max}} = 0.92 \Delta c_{l_{\max}} \dfrac{S_{fw}}{S_w} \cos \wedge, \nonumber\]

donde\(\wedge\),\(S_{fw}\), y ya\(S_w\) se conocen y\(c_{l_{\max}}\) se dieron en la Ecuación (\(\ref{eq3.5.34}\)). Por lo tanto,\(\Delta C_{L_{\max}} = 0.334\).

\(C_{L_{\max_f}}\)rinde entonces 1.8.

f.\(V_{stall}\):

Sabiendo que\(L = C_L \cdot \tfrac{1}{2} \rho S_w V^2\), que se puede considerar que el vuelo está balanceado, es decir\(L = m \cdot g\), y que la velocidad de calado se produce cuando el coeficiente de sustentación es máximo, tenemos que:

\[V_{stall} = \sqrt{\dfrac{m \cdot g}{\tfrac{1}{2} \rho S_w C_{L_{\max}}}} = 44.56 \ m/s.\nonumber\]

Para el caso de configuración completa, utilizamos\(C_{L_{\max_f}}\) y consideramos la superficie húmeda de ala y aleta (observe que no estamos incluyendo la extensión de cuerda en la superficie húmeda del ala). La velocidad de calado rinde:

\[V_{stall_f} = \sqrt{\dfrac{m \cdot g}{\tfrac{1}{2} \rho (S_w + S_{fw}) C_{L_{\max_f}}}} = 37.8 \ m/s. \nonumber\]

g. Discusión:

Los dispositivos de elevación alta están diseñados para aumentar el coeficiente máximo de elevación. Por su despliegue, incrementan la cuerda aerodinámica y la curvatura del perfil aerodinámico, modificando así la geometría del perfil aerodinámico para que la velocidad de calado durante fases específicas de vuelo como aterrizaje o despegue se reduzca significativamente, permitiendo volar más lento que en crucero.

El despliegue de dispositivos de alta elevación también aumenta el coeficiente de arrastre de la aeronave. Por lo tanto, para cualquier peso y velocidad aerodinámica dados, los flaps desviados aumentan la fuerza de arrastre. Los flaps aumentan el coeficiente de arrastre de una aeronave debido a la mayor resistencia inducida causada por la distribución distorsionada de sustentación en el ala con flaps extendidos. Algunos dispositivos aumentan el área de forma plana del ala y, para cualquier velocidad dada, esto también aumenta el componente de arrastre parásito de la resistencia total.

Al disminuir la velocidad de operación y aumentar la resistencia, el dispositivo de alta elevación acorta las distancias de despegue y aterrizaje, así como mejora la tasa de ascenso. Por lo tanto, estos dispositivos son fundamentales durante el despegue (reducir la velocidad a la que los levantamientos de la aeronave equivalen al peso de la aeronave), durante la fase inicial de ascenso (aumenta la velocidad de ascenso para evitar obstáculos) y aterrizaje (disminuir la velocidad de impacto y ayudar a frenar la aeronave).

---

4. Con base en los datos dados en la Figura 3.31.