12.2: Orientación entre marcos de referencia
- Page ID
- 87363
De acuerdo con la mecánica clásica, para orientar sin pérdida de generalidad un sistema de marco de referencia\(F_I\) con respecto a otro\(F_F\): si ambos tienen origen común, es necesario realizar una rotación genérica hasta que el eje coincida; si el origen difiere, es necesario, junto con lo mencionado rotación, una traslación para hacer coincidir los orígenes.
Existen diferentes métodos para orientar dos sistemas con origen común, como por ejemplo, cosinos directores, cuaterniones o los ángulos de Euler, que de hecho serán utilizados en esta disertación.
Los ángulos de Euler representan tres rotaciones compuestas y finitas dadas en un orden preestablecido que mueven un marco de referencia a un marco referido dado. Esto equivale a decir que cualquier orientación se puede lograr componiendo tres rotaciones elementales y finitas (rotaciones alrededor de un solo eje de una base), y también equivalente a decir que cualquier matriz de rotación puede descomponerse como producto de tres matrices de rotación elementales.
El orden preestablecido de rotaciones elementales suele denominarse Convención. En aeronáutica y vehículos espaciales se utiliza universalmente la Convención Tailt-Bryan. Dicha convención también se conoce como Convención 321.
Si se\(F_I\) conocen los tres componentes de un vector\(\vec{A}\) en, la matriz de transformación o rotación\(L_{F_I}\) expresa un vector\(\vec{A}\) en el sistema de referencia de la\(F_F\) siguiente manera:
\[\vec{A}_F = L_{F_I} \vec{A}_I\]
\(L_{F_I}\)se puede obtener simplemente obteniendo las tres matrices de rotación individuales y multiplicándolas adecuadamente.
Dados dos sistemas de referencia\(F_F\),\(F_I\) y, con origen común, queremos hacer\(F_I\) coincidir con\(F_F\): primero giramos\(F_I\) alrededor del eje\(z_I\) un ángulo\(\delta_3\), obteniendo los primeros sistemas de referencia intermedios\(F_1\). Segundo, giramos el sistema\(F_1\) alrededor del eje\(y_1\) un ángulo\(\delta_2\), obteniendo el segundo sistema de referencia intermedio\(F_2\). Tercero, giramos el sistema\(F_2\) alrededor del eje\(x_2\) un ángulo\(\delta_1\), obteniendo el sistema de referencia final\(F_F\).
Primero, expresamos el vector unitario de\(F_1\) como una función del vector unitario de\(F_I\):
\[\begin{bmatrix} \vec{i}_1 \\ \vec{j}_1 \\ \vec{k}_1 \end{bmatrix} = \begin{bmatrix} \cos \delta_3 & \sin \delta_3 & 0 \\ -\sin \delta_3 & \cos \delta_3 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \vec{i}_I \\ \vec{j}_I \\ \vec{k}_I \end{bmatrix}\]
La matriz de rotación será:
\[L_{1I} = R_3 (\delta_3) = \begin{bmatrix} \cos \delta_3 & \sin \delta_3 & 0 \\ -\sin \delta_3 & \cos \delta_3 & 0 \\ 0 & 0 & 1 \end{bmatrix}.\]
donde\(R_3 (\delta_3)\) es la notación de la matriz individual de rotación de un ángulo\(\delta_3\) alrededor del tercer eje (eje\(z\)).
Por lo tanto, el vector\(\vec{A}\) expresado en el primer marco de referencia intermedio\(F_1\) (Notado\(\vec{A}_1\)) será:
\[\vec{A}_1 = L_{1I} \vec{A}_I.\]
Operando análogamente para la segunda rotación individual:
\[\begin{bmatrix} \vec{i}_1 \\ \vec{j}_1 \\ \vec{k}_1 \end{bmatrix} = \begin{bmatrix} \cos \delta_2 & 0 & -\sin \delta_2 \\ 0 & 1 & 0 \\ \sin \delta_2 & 0 & \cos \delta_2 \end{bmatrix} \begin{bmatrix} \vec{i}_1 \\ \vec{j}_1 \\ \vec{k}_1 \end{bmatrix}\]
\[L_{21} = R_2 (\delta_2) = \begin{bmatrix} \cos \delta_2 & 0 & -\sin \delta_2 \\ 0 & 1 & 0 \\ \sin \delta_2 & 0 & \cos \delta_2 \end{bmatrix}\]
\[\vec{A}_2 = L_{21} \vec{A}_1.\]
Por último, para la tercera rotación individual:
\[\begin{bmatrix} \vec{i}_F \\ \vec{j}_F \\ \vec{k}_F \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \delta_1 & \sin \delta_1 \\ 0 & -\sin \delta_1 & \cos \delta_1 \end{bmatrix} \begin{bmatrix} \vec{i}_2 \\ \vec{j}_2 \\ \vec{k}_2 \end{bmatrix}\]
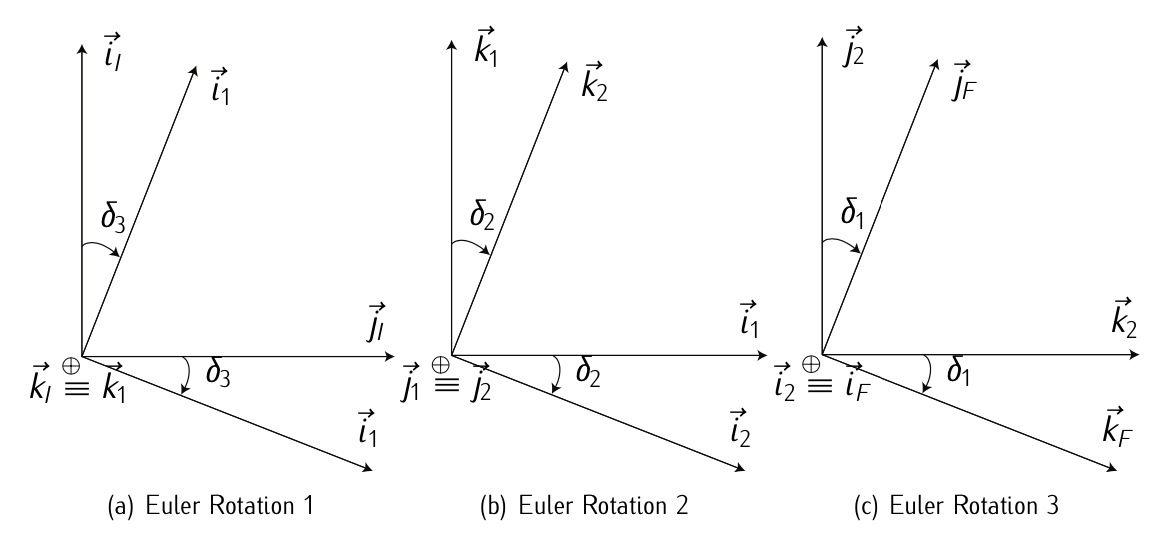
Figura 12.1: Ángulos más llenos
\[L_{F2} = R_1 (\delta_1) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \delta_1 & \sin \delta_1 \\ 0 & -\sin \delta_1 & \cos \delta_1 \end{bmatrix}\]
\[\vec{A}_F = L_{F2} \vec{A}_2.\]
Componiendo:
\[\vec{A}_F = L_{F2} L_{21} L_{1I} \vec{A}_I,\]
y la matriz de rotación global será:
\[L_{FI} = \begin{bmatrix} \cos \delta_2 \cos \delta_3 & \cos \delta_2 \sin \delta_3 & -\sin \delta_2 \\ \sin \delta_1 \sin \delta_2 \cos \delta_3 - \cos \delta_1 \sin \delta_3 & \sin \delta_1 \sin \delta_2 \sin \delta_3 + \cos \delta_1 \cos \delta_3 & \sin \delta_1 \cos \delta_2 \\ \cos \delta_1 \sin \delta_2 \cos \delta_3 + \sin \delta_1 \sin \delta_3 & \cos \delta_1 \sin \delta_2 \sin \delta_3 - \sin \delta_1 \cos \delta_3 & \cos \delta_1 \cos \delta_2 \end{bmatrix}\]


