1.4: Envasado de Biomasa- Densificación y Requerimientos
- Page ID
- 80973
Shahab Sokhansanj, Ph.D., P.Eng.
Universidad de Saskatchewan
Saskatoon, Saskatchewan, Canadá
| Términos Clave |
| Capacidad de campo | Densidad de pacas | Empacado redondo |
| Capacidad de material | Almacenamiento de pacas | Empacado cuadrado |
Variables
Introducción
Un tema importante en un sistema de bioenergía basado en biomasa es el transporte de materia prima desde el campo hasta la instalación de procesamiento. El empacado, que es el empaque denso de biomasa en una forma manejable, es de importancia porque es un proceso que consume energía que determina la eficiencia del sistema bioenergético. La densidad de pacas es el factor más importante que influye en la logística (número de vehículos, volumen de almacenamiento, duración del uso) y costo (mano de obra y energía) de la recolección y entrega de biomasa a una biorrefinería. A menos que la biomasa esté empaquetada a una densidad suficiente, la energía requerida para el transporte puede exceder la liberación de energía por los procesos de bioconversión. En este capítulo se analizan dos tipos de empacadoras, redondas y cuadradas; la relación entre la densidad de biomasa y la energía requerida para hacer pacas; y los pros y los contras de los diferentes tipos de pacas. El capítulo discute métodos adecuados para el manejo de pacas con el fin de minimizar las pérdidas de materia seca durante el almacenamiento.
Conceptos
El aporte de energía y poder a la calidad de vida es indispensable. Los países que gozan de una alta calidad de vida son los que más energía consumen per cápita. Los combustibles generan energía para operar fábricas, movilizar el transporte motorizado y calentar y enfriar edificios. Hasta el siglo XVI, la mayor parte de la energía provenía ya sea directamente del sol o indirectamente por la quema de biomasa, principalmente madera y otro material vegetal. La introducción del carbón trajo una nueva era en el desarrollo industrial. Para el siglo XIX, el petróleo y el gas revolucionaron el desarrollo industrial.
El desarrollo de la agricultura ocurrió en paralelo con la explotación de nuevas fuentes de energía. Los agricultores abandonaron prácticas agrícolas desgarradoras y adoptaron equipos motorizados como tractores y cultivadores. Los agricultores que habían usado herramientas manuales para cortar y apilar un cultivo en el campo comenzaron a utilizar máquinas que podían hacer estas tareas de manera más eficiente. Se desarrollaron grandes equipos de preparación de tierras, aplicadores de fertilizantes y equipos de protección de cultivos, junto con nuevos equipos de cosecha, manejo y transporte. Esto fue posible gracias a los productos de combustibles fósiles como la gasolina y el diesel.
Herramientas de mecanización impulsadas por combustibles fósiles para producir abundantes alimentos y ropa para la humanidad hasta el día de hoy. Desafortunadamente, el uso de combustibles fósiles resultó en algunas consecuencias inesperadas. El dióxido de carbono adicional (CO 2) y otros gases liberados de la combustión de combustibles fósiles incrementaron la concentración de gases de efecto invernadero en la atmósfera impactando o contribuyendo a los efectos del cambio climático. Con el tiempo, los combustibles fósiles se volverán caros para los agricultores debido a la disponibilidad limitada y las sanciones basadas en políticas por causar emisiones contaminantes no deseadas del aire. Se ha incrementado el enfoque en las fuentes de energía renovables como alternativa para desplazar los combustibles fósiles en la sociedad. La biomasa, por ejemplo, se puede utilizar de manera mucho más eficiente más allá de la quema convencional como materia prima para producir biocombustibles.
La industria de fabricación de equipos agrícolas ha desarrollado una serie de máquinas para cosechar y manejar granos, frutas y verduras después de la cosecha. Los residuos como las pajitas y las hojas han tenido tradicionalmente poco valor financiero, por lo que la industria no había desarrollado muchas máquinas para explotar cultivos enteros o residuos, sino que se enfocaba en extraer solo la parte valiosa de los cultivos, como el grano y la fruta. La parte restante del cultivo como paja, hojas y ramas se dejaron en el campo en su mayoría sin usar.
Desde finales del siglo XX, ha habido una demanda de equipos para recolectar y empaquetar pajitas, pastos y plantas enteras, lo que coincidió con otros desarrollos como las restricciones a la quema de residuos (por la calidad del aire) y la operación de sistemas de labranza de conservación. La industria de equipos agrícolas ha desarrollado equipos, como empacadoras, para reunir plantas enteras, pajitas y pastos en paquetes redondos o cuadrados de densidad mucho mayor que la que se puede lograr mediante el apilamiento pasivo del material. Las pacas densas ocupan menos espacio para almacenar y transportar biomasa.
Densificación
El empacado es el método más utilizado para densificar y empaquetar biomasa en la granja (Figura 1.4.1). Densidad es la masa de biomasa en la paca dividida por el volumen de la bala:
\[ \rho=\frac{M}{V} \]
donde ρ = densidad (kg/m 3)
M = masa de la paca (kg)
V = volumen de pacas (m 3)
La densidad de pacas típicamente varía de 140 a 240 kg/m 3 dependiendo del tipo de biomasa y la presión utilizada sobre la biomasa al formar la paca. La densidad de pacas influye en el costo de embalar y entregar biomasa hasta el punto de su uso. La recolección, el almacenamiento, el transporte y el procesamiento pueden aportar hasta el 50% del costo de la materia prima de bioenergía (Shinners y Friede, 2018), por lo que esta es una consideración importante a la hora de operar el sistema. El equipo de transporte tiene un volumen y masa máximos (carga útil) por remolque, por lo que optimizar la densidad de pacas minimiza los costos de transporte. La creación de una bala densa requiere energía para formar la paca y energía para transportarla durante la operación. Las pacas se pueden apilar en una ubicación de la granja antes de transportarlas a una instalación de bioenergía. Para aplicaciones energéticas, las pacas densas se transportan típicamente a una instalación de peletizado donde las pacas se rompen y se vuelven a compactar en pellets más densos.
Una gama de cultivos de biomasa son embalados, como la alfalfa (Medicago sativa), timoteo (Phleum pretense), gramíneas en general (Poaceae), trigo (Triticum spp.), maíz/maíz (Zea mays) y soya (Glycine max). Los cultivos de biomasa pueden ser cosechados como plantas enteras (segadas) o separados en el campo usando una cosechadora que divide el grano del otro material vegetal. Independientemente del cultivo, cuando se corta en campo, el material que se embalará se deja como hileradora (una pila lineal de material de baja densidad paralela a la dirección de desplazamiento de la máquina). Los materiales generalmente se dejan en la hilerera para que se sequen. El contenido de humedad ideal para un embalaje y almacenamiento seguros depende del cultivo, pero normalmente es inferior al 30%. Puede haber pérdidas por rotura si el contenido de humedad del campo es demasiado bajo, o el equipo debe usar energía innecesariamente si está demasiado húmedo. La biomasa húmeda puede estropearse debido al crecimiento de hongos y bacterias durante el almacenamiento, lo que puede interferir con los procesos de refinación para fabricar biocombustibles. Dependiendo del clima, el tiempo que la planta permanece en el campo para secarse varía de unas pocas horas a unos días. Cuando está lista, una empacadora recoge el material de la hilera para formar pacas. Las empacadoras modernas son móviles, es decir, el equipo se mueve por el campo.

Varios factores determinan la elección entre pacas redondas o cuadradas. Las pacas redondas son preferidas en regiones más húmedas ya que pueden arrojar la lluvia. Las pacas cuadradas son preferidas en regiones secas ya que se apilan mejor. En Norteamérica, las granjas más pequeñas tienden a usar empacadoras redondas y las granjas más grandes tienden a usar empacadoras cuadradas grandes. En el Cuadro 1.4.1 se enumeran algunas características de las empacadoras que operan en granjas norteamericanas. En algunos países, como Irlanda, los pequeños agricultores tienden a favorecer las pacas cuadradas pequeñas ya que son más fáciles de manejar una vez hechas.
| Categorías de pacas | Dimensiones (ancho × profundidad × largo para cuadrado; diámetro × profundidad para redondo) | Masa (kg) | Tamaño de la granja | Productividad | Costo Típico ($/h) |
|---|---|---|---|---|---|
|
Cuadrado pequeño |
356 × 457 × 914 mm |
24 |
Granjas pequeñas |
Bajo |
120 |
|
Cuadrado grande |
914 × 1219 × 2438 mm |
435 |
Granjas |
Alto |
250 |
|
Redonda pequeña |
1219 × 1219 mm |
228 |
Granjas pequeñas |
Mediano |
130 |
|
Redonda grande |
1829 × 1829 mm |
769 |
Granjas |
Alto |
150 |
Empacado Cuadrado
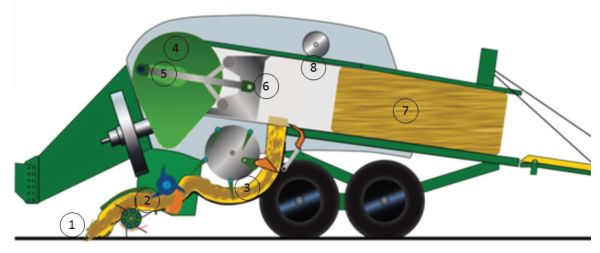
Una empacadora cuadrada (Figura 1.4.2) consiste en un mecanismo de recogida (1) para levantar la biomasa de la hilera y entregarla en rollos de alimentación (2). Un juego de cuchillos en una rueda giratoria (3) corta la biomasa a una longitud establecida. Un brazo pitman (5) conecta un volante (4) excéntricamente (descentrado) a un émbolo (6). Esta disposición convierte la rotación del volante en un movimiento de vaivén, para mover el émbolo hacia adelante y hacia atrás en la cámara de pacas.
La potencia necesaria para formar la paca proviene de la toma de fuerza del tractor (PTO). Cada rotación sumerge la biomasa a medida que ingresa a la cámara de empacado. El émbolo reciprocante comprime el material suelto para formar una paca. El proceso de alimentar heno a la cámara de pacas y comprimirlo se repite hasta que se forma la paca. La densidad de la paca se determina ajustando las barras de tensión superior e inferior accionadas por resorte o hidráulicas en la cámara de la paca. Una rueda de medición de bala (8) gira a medida que la bala se mueve a través de la cámara de pacas.
La longitud de la bala se controla ajustando el número de rotaciones de la rueda de medición. El mecanismo de atado (9) está sincronizado con el movimiento del émbolo. Cuando el émbolo está en su posición trasera y la biomasa está completamente comprimida, un juego de agujas entrega el cordel al mecanismo de atado. A medida que el cordel es agarrado por el mecanismo de atadura, las agujas se retraen y se ata la paca. Una vez comprimida y atada, la paca es expulsada de la cámara de pacas. Las pacas cuadradas generalmente se producen en varios tamaños (Cuadro 1.4.1) y el peso depende del diseño de la empacadora, el tipo de biomasa y el contenido de humedad, pero típicamente oscila entre 24 y 908 kg.
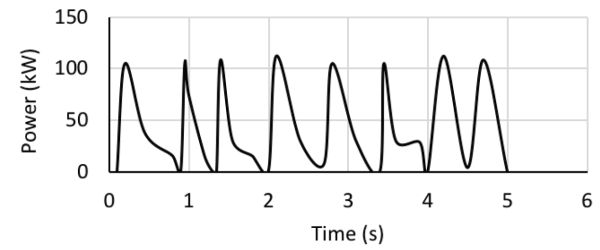
La Figura 1.4.3 muestra una gráfica de requerimientos instantáneos de potencia para una empacadora cuadrada (PAMI, 1990). Los requisitos de potencia máxima son el resultado de la acción del émbolo. En un cultivo típico de alfalfa, la entrada de potencia promedio varió de 23 a 30 kW mientras que la entrada de potencia máxima instantánea fue de 110 kW. Los requisitos de potencia promedio de la barra de tracción para remolcar la empacadora en campo variaron de 5 a 8 kW y alcanzaron un máximo de 20 kW en campos blandos o montañosos. Para utilizar completamente la capacidad de la empacadora, PAMI (1990) recomienda un tractor con una potencia de toma de fuerza mínima de 68 kW (90 hp). Se requeriría un tractor con una clasificación PTO de 83 kW (110 hp) en condiciones montañosas.
Empacadora Redonda
Una empacadora redonda (Figura 1.4.4) forma la biomasa en una bala cilíndrica. La empacadora redonda recoge la biomasa de la hileradora utilizando dientes similares a dedos, hechos de acero para muelles o un material de polietileno fuerte, y enrolla la biomasa dentro de la cámara de pacas usando rodillos anchos o cintas.
Una empacadora redonda viene en dos tipos. Aquellos con una cámara de tamaño fijo utilizan rodillos de posición fija (Figura 1.4.5a), y aquellos con cámara variable usan correas flexibles (Figura 1.4.5b). Una cámara fija hace pacas con un núcleo blando. Una cámara variable hace pacas con un núcleo duro. Una paca de núcleo blando es “transpirable”, lo que significa que la porosidad es suficiente para que la paca continúe secándose cuando se deja en el campo. El tamaño de la paca permanece fijo por el tamaño de la cámara. En una cámara variable, una serie de resortes y palancas retráctiles aseguran que se forme una paca apretada desde el núcleo hasta la circunferencia. El operador establece el diámetro de la bala y una masa objetivo para lograr la densidad requerida. Después de la formación de la paca, se detiene el movimiento hacia adelante de la máquina y el flujo de entrada de biomasa. El cordel o una red se envuelve alrededor de la circunferencia de la paca usando un brazo móvil. Una vez que la red ha cercado la paca suficientes veces para mantener la forma y contener suficientemente el material, los brazos vuelven a la posición inicial y se cortan los hilos de cordel o de la red. La envoltura neta cubre más área de superficie de la paca, evitando la pérdida de material y manteniendo fácilmente la forma de la paca.

Una vez que la paca se forma y se envuelve, se expulsa de la cámara de pacas. Algunas empacadoras redondas tienen “pateadoras” hidráulicas, mientras que otras están cargadas por resorte o dependen del giro de la paca para sacar la paca de la cámara. Una vez que la paca ha sido expulsada de la empacadora, se cierra la puerta trasera a la cámara, y la máquina comienza a avanzar, incorporando biomasa hasta que la siguiente paca esté lista. Las empacadoras redondas grandes de cámara variable suelen producir pacas de 1.2 a 1.8 m de diámetro y hasta 1.5 m de ancho, con un peso de 500 a 1000 kg, dependiendo del tamaño, material y contenido de humedad. Una densidad típica de pacas redondas varía de 140 kg/m 3 a 180 kg/m 3.
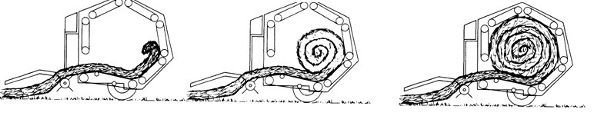
a) Configuración de cámara fija
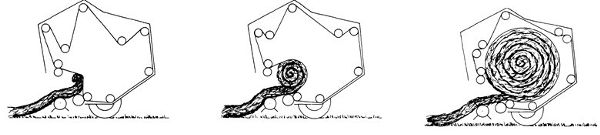
(b) Configuración de cámara variable
Figura\(\PageIndex{5}\): Los dos tipos de empacadoras redondas, (a) cámara fija y (b) cámara variable (Freeland y Bledsoe, 1988).
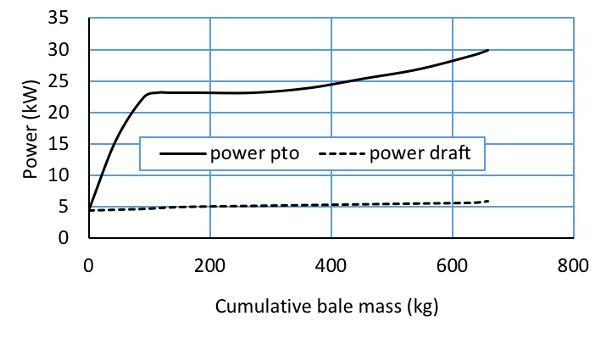
La Figura 1.4.6 muestra los requisitos típicos de potencia de PTO y barra de tracción para la empacadora redonda John Deere 535 con una capacidad de material de 16.1 t/h (PAMI, 1992). La potencia instantánea registrada por el tractor se grafica contra el peso de la paca para mostrar el aumento en la entrada de energía mientras se forma cada fardo. Las curvas son un promedio de los datos de PTO medidos altamente fluctuantes, que variaron de 5 a 8 kW sin carga hasta un máximo de 32 kW en alfalfa para pacas de tamaño completo. La entrada de potencia de toma de fuerza depende en gran medida de la capacidad del material (t/h Los requisitos de potencia de la barra de tiro a 11.5 km/h fueron de aproximadamente 8 kW cuando la bala alcanzó un tamaño completo. Aunque los requisitos máximos de caballos de fuerza no excedieron los 38 kW, se requirió potencia adicional para adaptarse a otras condiciones de campo como campos blandos y montañosos. El fabricante sugirió un tractor de 56 kW (75 hp) para utilizar completamente la capacidad de la empacadora.
Evaluación del rendimiento de empacado
Los Estándares ASABE EP496 y D497 (Estándares ASABE, 2015a, b) definen el desempeño de los equipos de campo en términos de capacidad de campo y capacidad de material.
Capacidad de Campo
La capacidad de campo cuantifica la tasa de tierra procesada (área por unidad de tiempo) como:
\[ C_{a}=\frac{SWE_{f}}{10} \]
donde C a = área de campo cubierta por unidad de tiempo (ha/h)
S = velocidad de campo promedio del equipo durante la cosecha (km/h)
W = ancho efectivo (m)
E f = eficiencia de campo (decimal) (Tabla 1.4.2)
La velocidad de campo, S, puede variar de 4 a 13 km/h (Cuadro 1.4.2). Este rango representa la variabilidad en las condiciones de campo que afecta la velocidad de desplazamiento del equipo.
El ancho efectivo, W, es el ancho sobre el que trabaja la máquina. Puede ser más ancho o más estrecho que el ancho medido de la máquina dependiendo del diseño, cómo se usa la máquina en el campo con otros equipos y la experiencia y habilidad del operador. El ancho efectivo podría estar determinado por el ancho de corte de una segadora delante de la empacadora, cuando un rastrillo de rueda reúne el cultivo segado en una franja para que la empacadora recoja.
La eficiencia de campo, E f (Cuadro 1.4.2), es la relación entre la productividad de una máquina en condiciones de campo y la productividad máxima teórica. La eficiencia de campo explica la falta de utilización del ancho de operación teórico de la máquina, el tiempo perdido debido a la falta de habilidad del operador, paradas frecuentes y características de campo que causan interrupciones en la operación regular. Los viajes hacia y desde un campo, las reparaciones mayores, el mantenimiento preventivo y las actividades diarias de servicio no se incluyen en los cálculos de tiempo de campo o eficiencia de campo.
La eficiencia del campo no es una constante para una máquina en particular, sino que varía según el tamaño y la forma del campo, el patrón de operación del campo, el rendimiento del cultivo, la humedad del cultivo y otras condiciones. La mayor parte del tiempo perdido en campo se debe al giro y al desplazamiento inactivo, al tiempo de manejo de materiales, a la limpieza del equipo obstruido, al ajuste de la máquina, a la lubricación y al reabastecimiento de combustible. Las empacadoras redondas tienen una eficiencia menor que las empacadoras cuadradas porque la forma de la bala redonda hace que el manejo, transporte y almacenamiento de la bala sea ineficiente en comparación con el manejo de una paca cuadrada (Kemmerer y Liu, 2011).
| Equipo de cosecha de biomasa | Eficiencia de Campo | Velocidad de campo | Observaciones | ||
|---|---|---|---|---|---|
| Rango (%) | Típico (%) | Rango (km/h) | Típico (km/h) | ||
|
Empacadora cuadrada pequeña |
60—85 |
75 |
4,0-10,0 |
6.5 |
Pacas pequeñas a medianas |
|
Empacadora cuadrada grande |
70—90 |
80 |
6.5—13.0 |
8.0 |
Pacas de tamaño mediano a grande |
|
Empacadora redonda grande |
55—75 |
65 |
5.0—13.0 |
8.0 |
Pacas redondas comerciales |
Capacidad de Material
La capacidad material es la masa de cultivo embalada por hora, y se calcula utilizando la capacidad de campo (C a) y el rendimiento del campo:
\[ C_{m}=C_{a}Y \]
donde C m = capacidad de material (t/h)
Y = rendimiento promedio del campo (t/ha); es la cantidad de biomasa que se corta y se coloca en la franja lista para embalar, no la biomasa total aérea en el campo.
Para cultivos cultivados con fines de suministro de energía, normalmente no se corta y empaca más del 50% de la biomasa aérea. En la práctica, el rendimiento (Y) puede ser tan bajo como 25-30% de la biomasa total sobre el suelo. El 70— 75% restante de la biomasa se deja en el campo para fines de conservación del suelo. La eliminación de un mayor porcentaje también puede recoger suciedad no deseada y material extraño junto con la biomasa.
Requerimientos Energéticos
La densidad de pacas que se puede lograr depende de las especificaciones de la máquina (sus dimensiones y eficiencia) y la energía mecánica que se puede suministrar a la empacadora.
Requerimientos energéticos para pacas cuadradas
Partimos de definir presión y densidad con el fin de calcular la energía y la entrada de energía para hacer una paca cuadrada.
La presión, P, se calcula usando la fuerza sobre el área,
\[ P = F/A \]
donde A = área sobre la que se ejerce la fuerza (m 2)
\(f= \text{force (kN)}\)
La fuerza (kN) se deriva de la masa (M, kg),
\[ F= M (\text{kg}/1000) \times g \ (\text{m/}s^{2}) \]
donde g = aceleración por gravedad (9.81 m/s 2).
El requerimiento de potencia está relacionado con la densidad de pacas. La relación se determina primero relacionando la presión con la densidad, luego calculando la energía a partir de la fuerza vs. desplazamiento, y finalmente estimando la potencia a partir de la tasa de tiempo de energía.
Para el primer paso, una ecuación comúnmente utilizada para relacionar presión y densidad es (Van Pelt, 2003; Afzalinia y Roberge, 2013):
\[ P = (\frac{1}{k} \rho)^{1/n} \ \ \ _{k,n \ > \ 0} \]
| Cultivo de biomasa | k | n |
|---|---|---|
|
Stover |
29.48 |
0.330 |
|
Paja de trigo |
38.79 |
0.293 |
|
Switchgrass |
100.99 |
0.137 |
donde P = la presión ejercida por el émbolo (kPa)
k y n = constantes positivas
\( \rho = \text{density (kg/}m^{3}) \)
Hofstetter y Liu (2011) sugirieron valores para k y n para varios cultivos (Cuadro 1.4.3).
Durante la formación de la paca, la densidad inicial es cero (cámara vacía), y aumenta constantemente a la densidad máxima posible dada la presión del émbolo.
El siguiente paso es calcular la energía a partir de la fuerza y el desplazamiento. El aporte de energía total requerido para hacer una paca se calcula integrando el área bajo la curva de presión-desplazamiento de 0 a P máx. Esta integración produce entrada de energía por unidad de masa (E) para una sola carrera del émbolo para formar lo que se conoce como oblea. La ecuación 1.4.7 representa la integración de fuerza vs. desplazamiento:
\[ E= \int_{0}^{P_{max}} (\frac{1}{\rho})dP \]
donde P = presión (kN/m 2)
E = entrada de energía por unidad de masa (kJ/kg)
Sustituyendo ρ de la Ecuación 1.4.6 e integrando rendimientos:
\[ E= \frac{1}{(1-n)k}P_{max}^{(-n+1)} \]
Reemplazar P max por ρ max permite una estimación de energía específica, E (kJ/kg):
\[ E=\frac{1}{(1-n)k}(\frac{1}{k}\rho_{max} \ ^{\frac{1-n}{n}}) \]
Al hacer una paca cuadrada, cada golpe del émbolo forma una oblea de alrededor de 51 mm de espesor. Requeriría alrededor de 19 golpes para hacer una paca de 915 mm. Para una paca completa la energía requerida, (E op, kJ), puede calcularse a partir de E multiplicada por la masa final de la paca,
\[ E_{op} = E \times M \]
Para el último paso, la potencia (energía por unidad de tiempo) requerida para hacer una bala se calcula multiplicando la energía específica (E) por la capacidad del material (C m)
\[ P_{opt}=\frac{C_{m}E_{op}}{3.6e} \]
donde P opt = potencia teórica para operar la empacadora cuadrada (kW)
e = factor de eficiencia que da cuenta de ineficiencia en la transmisión de potencia de la PTO a la empacadora
En la práctica, la norma ASABE D497 (Estándares ASABE, 2015a) sugiere que se necesitan aproximadamente 4 kW para que una empacadora funcione vacía, por lo que esta sobrecarga de energía debe agregarse a P opt.
Requerimientos de Energía para Pacas Redondas
Para una empacadora redonda, ASABE Engineering Practice EP 496 (ASABE Standards, 2015b) recomienda estimar la potencia de operación para empacadoras y otras máquinas rotativas usando:
\[ P_{op}=a+bW+cF_{w} \]
donde P op = toma de fuerza requerida para operar la empacadora redonda (kW)
W = ancho de trabajo de la empacadora (m)
F w = velocidad de alimentación del material, masa húmeda (t/h)
a, b y c = parámetros específicos de la máquina (Tabla 1.4.4)
| Tipo de Empacadora | a (kW) | b (KW/m) * | c (kWh/t) |
|---|---|---|---|
|
Cuadrado pequeño |
2.0 |
0 |
1.0 |
|
Cuadrado grande |
4.0 |
0 |
1.3 |
|
Gran cámara redonda y variable |
4.0 |
0 |
1.1 |
|
Gran cámara redonda y fija |
2.5 |
0 |
1.8 |
|
* Se reportan valores distintos de cero para maquinaria como segadoras y rastrillos. |
|||
Comparando los requerimientos de potencia, Tremblay et al. (1997) encontraron que la empacadora de cámara variable requería una potencia promedio de PTO de 10.2 kW en comparación con una empacadora de cámara fija que requirió una potencia promedio de PTO de 13.3 kW. Además, la potencia pico de PTO requerida fue considerablemente menor para la cámara variable (14.5 kW) en comparación con la cámara fija (37.5 kW). Esto significa que normalmente se requeriría un tractor mucho más grande para operar una empacadora de cámara fija. Para un funcionamiento flexible en términos de tractor requerido y tamaño y densidad de pacas, una empacadora redonda de cámara flexible es quizás la mejor opción.
Requisitos de energía para tirar de una empacadora
La potencia requerida para accionar el tractor y remolcar la empacadora se determina a partir de la fuerza de tiro (D, kN):
\[ D=r\ m\ g\ /\ 1000 \]
donde r = relación, resistencia al desplazamiento
m = masa del equipo tirado y su carga (kg)
g = constante de aceleración gravitacional = 9.81 m/s 2
La resistencia al desplazamiento es una fuerza de tiro adicional que debe incluirse en los requisitos de potencia de cómputos. Los valores de resistencia al desplazamiento dependen de las dimensiones de las ruedas de transporte, la presión de los neumáticos, el tipo de suelo y la humedad del Las relaciones de resistencia al movimiento se definen en ASAE S296 (ASABE Standards, 2018). El valor de r se puede estimar utilizando (ASABE Standards, 2015a):
| Condición de la superficie | B n | sl | Barra de tracción X d [a] |
|---|---|---|---|
|
Hormigón duro |
80 |
0.04—0.08 |
0.88 |
|
Suelo firme |
55 |
0.08—0.10 |
0.77 |
|
Suelo labrado |
40 |
0.11—0.13 |
0.75 |
|
Suelo blando |
20 |
0.14—0.16 |
0.70 |
|
[a] X d representa la relación entre la potencia de tiro y la potencia de toma de fuerza. Los valores enumerados son para tractores con tracción a las 4 ruedas. |
|||
\[ r=\frac{1}{B_{n}}+0.04+\frac{0.5sl}{\sqrt{B_{n}}} \]
donde B n = factor índice de suelo (Cuadro 1.4.5)
sl = valor decimal que representa el deslizamiento de la rueda del tractor (Tabla 1.4.5)
Dada la velocidad y la fuerza de tiro (kN), la potencia de tiro se calcula mediante:
\[ P_{d}=\frac{DS}{3.6} \]
donde P d = la potencia de tiro (tracción) del tractor (kW)
S = la velocidad promedio de avance de la empacadora (km/h)
Aplicaciones
Manejo y Almacenamiento de Pacas
Apilamiento
Una vez hechas las pacas, deben ser retiradas del campo antes de que se pueda preparar la tierra para la siguiente cosecha. Los tractores y cargadores equipados con dispositivos de agarre recogen y cargan las balas en un remolque para transportarlas fuera del campo. Luego, las pacas se apilan al lado del campo o en un sitio de almacenamiento central mediante el uso de un tractor o un cargador. HSE (2012) recomienda construir pilas sobre terreno firme, seco, nivelado y de drenaje libre, que debe estar abierto y bien ventilado, lejos de los postes eléctricos superiores. Se recomienda el uso de piedras o roca triturada en el suelo debajo de una pila para nivelarla y evitar que el agua suba a la pila. El sitio debe estar alejado de cualquier posible peligro de incendio y fuentes de ignición con un buen acceso por carretera para que las pacas puedan transportarse hacia y desde la pila de manera segura. Debe haber suficiente espacio para que los tractores, remolques y otros vehículos tengan espacio adecuado para maniobrar.
La Figura 1.4.7 muestra la configuración correcta de pacas cuadradas apiladas y pacas redondas, con una base ancha que se estrecha a medida que aumenta la pila. La altura máxima de la pila no debe ser mayor a 1.5 veces el ancho de la base. Generalmente, se recomienda una pila de no más de 10 pacas en superficies duras y 8 pacas en superficies blandas. Las pacas cuadradas deben colocarse con cada fila está desplazada de la fila de abajo, de tal manera que no haya un hueco continuo entre ellas. Las pacas redondas se apilan en una pirámide con menos pacas en cada dirección que en la capa inferior. Las pacas redondas exteriores necesitan un calzo en cada una de las pacas en la capa más baja para evitar que se desenrollen (Figura 1.4.7). Al igual que con las pacas cuadradas, las pacas redondas deben colocarse para cubrir la brecha entre dos pacas debajo.
Una vez que se forma una pila, el peso de cada bala se convierte en un problema para la estabilidad de la pila. El peso de una paca grande puede oscilar entre 300 kg y más de 500 kg. Las pacas en la parte superior presionan sobre las pacas inferiores provocando su lenta deformación. El grado de deformación depende de la densidad de la paca y del contenido de humedad, y del tiempo que permanecen en la pila. Una bala de menor densidad y mayor humedad tiende a deformarse más que una bala de mayor densidad y una bala más seca.

Pérdida de Materia Seca
El contenido de humedad en el momento del empacado juega un papel importante en la cantidad de pérdida de materia seca que puede ocurrir durante el empacado y posteriormente durante el almacenamiento. Para biomasa frondosa como la alfalfa, el contenido de humedad recomendado para el empacado es menor de 30% y para almacenamiento menor de 15% a 20%; sin embargo, para un almacenamiento más prolongado, se prefiere un menor contenido de humedad de 10% a 12%. Las pacas cuadradas tienden a perder menos humedad que las pacas redondas, pero independientemente de su forma, es importante hacer las pacas lo más cerca posible de la humedad objetivo.
Las pérdidas pueden ser mecánicas y microbianas. Las pérdidas mecánicas ocurren principalmente durante el manejo de pacas, como construir la pila o quitar las balas de la pila. Algunas eliminaciones físicas de biomasa (conocida como lixiviación) también pueden tener lugar debido al lavado con lluvia. Además, los carbohidratos en la biomasa verde recién cortada pueden descomponerse a CO 2, agua y calor.
La pérdida de materia seca más prevalente se debe a la actividad microbiana, lo que provoca el deterioro del material vegetal y la pérdida de materia seca. El crecimiento de microbios en la biomasa está directamente relacionado con el contenido de humedad. La biomasa seca adsorbe la humedad de la lluvia cuando se expone y se convierte en un huésped para que se desarrolle moho. Tanto la cobertura como la duración del almacenamiento influyen en la pérdida de materia seca (Cuadro 1.4.6). Por ejemplo, la pérdida de materia seca de una paca descubierta en el suelo puede variar de 5% a 20% dentro de los 9 meses de almacenamiento. Si el tiempo de almacenamiento aumenta a 12 a 18 meses, la pérdida de materia seca puede aumentar de 20% a 35% de la masa de las pacas. Almacenar pacas bajo techo limitará las pérdidas de 2% a 5%. La investigación muestra que no hay mucha diferencia entre la pérdida de materia seca para pacas redondas y pacas cuadradas cuando se almacenan en condiciones similares (Wilcke et al., 2018).
| Método de Almacenamiento | Periodo de Almacenamiento (meses) | ||
|---|---|---|---|
| 0 a 9 | 12 a 18 | ||
|
Suelo |
Cubierto con una lona |
5—9 |
10—15 |
|
Expuesto |
5—20 |
20—35 |
|
|
Elevado |
Cubierto con una lona |
2—4 |
5—10 |
|
Expuesto |
3—15 |
12—35 |
|
|
Granero |
Encerrado |
~2 |
2—5 |
|
Lados abiertos |
2—5 |
3—10 |
|
El rango de pérdida de materia seca (Cuadro 1.4.6) proviene de diferencias en el clima, tipo de cultivo y contenido inicial de humedad de la biomasa. Sin embargo, estos números son buenos para tomar una decisión sobre el tipo de sistema de almacenamiento a elegir para las pacas. En términos de gasto de capital, almacenar en el suelo es lo menos costoso y almacenar en un granero cerrado es el más caro.
Factores de decisión para pacas cuadradas vs. redondas
La selección de pacas redondas o cuadradas depende de varios factores, incluyendo especies de cultivos a embalar, condiciones climáticas regionales, volumen de cultivo a cosechar, tipos de almacenamiento disponibles, potencia del tractor y servicios auxiliares disponibles. Las principales ventajas y desventajas de las pacas redondas y cuadradas se enumeran en la Tabla 1.4.7.
Ejemplos
| Baca Cuadrada | Baca Redonda |
|---|---|
| Ventajas | Ventajas |
|
• Utiliza más eficientemente el espacio en el transporte y almacenamiento • Mejor retención de forma durante el almacenamiento • Más fácil de apilar |
• Mayor disponibilidad de empacadoras y equipos de manejo • Menor precio para empacadoras • Mayor capacidad para arrojar agua si las pacas se almacenan descubiertas |
| Desventajas | Desventajas |
|
• Mayor absorción de humedad por pacas almacenadas sin cubierta |
• Uso menos eficiente del espacio en el transporte y almacenamiento de pacas • Una tendencia a que las pacas pierdan su forma durante el almacenamiento |
Ejemplo\(\PageIndex{1}\)
Ejemplo 1: Capacidad de campo y material
Problema:
Se corta un campo de heno mediante el uso de una cortadora de discos cortando franjas de 5 m. Después de unos días de secado, se utiliza un rastrillo rotatorio para hilar el heno para empacar. Calcular la capacidad de campo y la capacidad de material de tres empacadoras: cuadrado pequeño, cuadrado grande y redondo para un rendimiento de 7 t/ha de heno. ¿Qué máquina elegirías?
Solución
El ancho efectivo es de 5 m ya que este es el ancho de franja de la segadora. Calcular la capacidad de campo usando la Ecuación 1.4.2 y la capacidad material usando la Ecuación 1.4.3
\( C_{a}=\frac{SWE_{f}}{10} \)(Ecuación\(\PageIndex{2}\))
\( C_{m}=C_{a}Y \)(Ecuación\(\PageIndex{3}\))
donde C a = área de campo cubierta por unidad de tiempo (ha/h)
S = velocidad de campo promedio del equipo durante la cosecha (km/h)
W = ancho efectivo (m)
E f = eficiencia de campo (decimal)
C m = capacidad de material (t/h)
Y = rendimiento promedio del campo (t/ha)
Utilice los valores típicos de la Tabla 1.4.2 para la velocidad y eficiencia de cada tipo de empacadora. En el Cuadro 1.4.8 se enumeran los valores de entrada y los resultados del cálculo para la capacidad de campo y la capacidad La empacadora cuadrada grande puede procesar el área más grande por hora, por lo tanto, también puede procesar la mayor masa por hora. Así, con valores típicos de velocidad y eficiencia, se seleccionaría la empacadora cuadrada grande si los únicos criterios fueran el campo y la capacidad del material.
| Empacadora | Ancho de corte, W (m) |
Velocidad de campo, S (km/h) |
Eficiencia de campo, E f (%) |
Capacidad de campo, C a (ha/h) |
Rendimiento, Y (t/ha) |
Capacidad de material, C m (t/h) |
|---|---|---|---|---|---|---|
|
Empacadora cuadrada pequeña |
5 |
6.5 |
75 |
2.44 |
7 |
17.06 |
|
Empacadora cuadrada grande |
5 |
8.0 |
80 |
3.20 |
7 |
22.40 |
|
Empacadora redonda |
5 |
8.0 |
65 |
2.60 |
7 |
18.20 |
Ejemplo\(\PageIndex{2}\)
Ejemplo 2: Densidad y masa máximas de pacas
Problema:
Un agricultor está haciendo pacas cuadradas de tallo de maíz con 35% de contenido de humedad (base de masa húmeda). Las dimensiones de la paca comprimida son 914 mm × 1219 mm × 2438 mm. Determinar la densidad y masa máxima de cada paca dada la masa equivalente a la fuerza ejercida sobre la sección transversal (914 mm × 1219 mm) de la paca es de 20 toneladas (t).
Solución
La densidad máxima es una función de la presión máxima ejercida sobre la presión ejercida sobre la sección transversal de la paca. Primero, calcule la fuerza en la sección transversal de la paca (Ecuación 1.4.5) usando la masa equivalente dada de fuerza como 20 t, que es 20,000 kg, y la aceleración por gravedad como 9.8 m/s 2:
\( F= M\ (\text{kg/1000)} \times g\ (\text{m}/s^{2}) \)(Ecuación\(\PageIndex{5}\))
\( F= 20000 \times 9.8/1000 = 196 \text{ kN} \)
Calcule la presión ejercida sobre la sección transversal de la bala usando la Ecuación 1.4.4:
\( P=F/A \)(Ecuación\(\PageIndex{4}\))
\( P= 196 \text{ kN}/ (0.914 \times 1.219 \ m^{2}) = 175.92 \text{ kPa} \)
Calcular la densidad de pacas resolviendo la Ecuación 1.4.6 para ρ, utilizando los valores de k y n de la Tabla 1.4.3:
\( P_{max} = (\frac{1}{k}\rho)^{1/n} \ _{k,n \ >\ 0} \)(Ecuación\(\PageIndex{6}\))
\( \rho=kP^{n}=29.48(175.92)^{0.33}=162.1 \text{kg/}m^{3} \)
La masa de la paca se puede calcular a partir de la densidad y las dimensiones de la paca:
\( M = \rho V = 162.1 \text{ kg/}m^{3} \times (0.914 \times 1.219 \times 2.438 m^{3}) = 440.32 \text{kg} \)
Ejemplo\(\PageIndex{3}\)
Ejemplo 3: Energía específica y operativa
Problema:
Para la empacadora especificada en el Ejemplo 1.4.2, calcule la energía específica de la empacadora y, a partir de esta, la energía de operación requerida para hacer una paca.
Solución
Calcular energía específica usando la Ecuación 1.4.9:
\( E = \frac{1}{(1-n)k}(\frac{1}{k}\rho_{max}\ ^\frac{1-n}{n}) \)(Ecuación\(\PageIndex{9}\))
\( = \frac{1}{(1-0.33)29.48}(\frac{162.36}{29.48}) ^\frac{1-0.33}{0.33} \)
Ahora, calcule la energía de operación usando la Ecuación 1.4.10:
\( E_{op}=E\times M \)(Ecuación\(\PageIndex{10}\))
\( E_{op}= 1.62 \text{ kJ/kg} = 713.32 \text{ kJ} \)
Ejemplo\(\PageIndex{4}\)
Ejemplo 4: Potencia de funcionamiento
Problema:
Para la empacadora en los Ejemplos 1.4.2 y 1.4.3, la transmisión de potencia de la PTO del tractor a la empacadora no será 100% eficiente. Suponiendo 50% de eficiencia de transmisión de potencia desde el tractor hasta la empacadora, estime la potencia de operación que debe suministrarse a la empacadora.
Solución
Estimar la potencia teórica de operación, Popt, usando la Ecuación 1.4.11, con e = 0.50:
\( P_{opt}=\frac{C_{m}E_{op}}{3.6e} \)Ecuación\(\PageIndex{11}\))
\( P_{opt}=\frac{(22,400 \text{ kg/h}) \times 1.62 \text{ kJ/kg}}{(3600 \text{ s/h})(0.50)} = 20.16 \text{ kW} \)
Aplicando la aseveración ASABE D497 de que se necesitan aproximadamente 4 kW para que la máquina funcione cuando está vacía, el P opt es:
\( P_{opt}= 20.16+4=24.16 \text{ kW} \)
Ejemplo\(\PageIndex{5}\)
Ejemplo 5: Requisitos de potencia de una empacadora redonda
Problema:
Un agricultor tiene la opción de utilizar una empacadora redonda con cámara fija, una anchura de operación de 2 m, una ingesta de alimento de 18.2 t/h, y una masa de 15.800 kg, que produce pacas de 1.83 m de diámetro, 1.83 m de ancho o profundidad y 180 kg/m 3 de densidad. Calcular (a) el requerimiento de potencia para la empacadora redonda de cámara fija, (b) la fuerza de tiro de la máquina y (c) la potencia de tiro del tractor requerida para tirar de la máquina a través del campo.
Solución
- (a) La ecuación 1.4.12 puede ser utilizada para estimar el requerimiento de potencia. Una paca de casi 2 m de ancho sería considerada como una paca grande (Cuadro 1.4.1), por lo que los parámetros para la Ecuación 1.4.12 pueden tomarse de la Tabla 1.4.4 en consecuencia:
\( P_{opt}= a+bW+cF \)(Ecuación\(\PageIndex{12}\))
\( P_{opt}= 2.5+(0 \times 2)+(1.8 \times18.2)= 35.26 \text{kW} \)
- (b) La fuerza de tiro de la máquina se puede calcular utilizando la Ecuación 1.4.13:
\( D = r\ m\ g / 1000 \)(Ecuación\(\PageIndex{13}\))
- Primero, calcule la resistencia al movimiento, r, usando la Ecuación 1.4.14 con valores de la Tabla 1.4.5. Supongamos que la máquina está trabajando sobre una superficie de suelo blando y con deslizamiento promedio. Así, del Cuadro 1.4.5, B n = 20, sl = 0.15 (promedio de 0.14 y 0.16):
\( =\frac{1}{B_{n}}+0.04+\frac{0.5sl}{\sqrt{B_{n}}} \)(Ecuación\(\PageIndex{14}\))
\( r=\frac{1}{20}+0.04+\frac{0.5(0.15)}{\sqrt{20}} = 0.16771 \)
- A continuación, calcule la masa de pacas más empacadoras:
- Volumen de pacas: V = π r 2 L = 3.14 (0.915 m) 2 (1.83 m) = 4.814 m 3
- Masa de la paca: M = V ρ = 4.814 m 3 × 180 kg/m 3 = 866.5 kg
- Masa de paca más empacadora: m = 866.5 + 15,800 = 16,666.5 kg
- Sustituyendo valores en la Ecuación 1.4.13 arroja la fuerza de calado de la empacadora:
\( D = r\ m\ g\ / 1000 = (0.16771 \times 16,666.5 \times 9.81) /1000 = 27.4 \text{ kN} \)
- c) A partir de la fuerza de tiro, calcule la potencia de calado, P d, para la velocidad dada, S, usando la Ecuación 1.4.15:
\( P_{d}=\frac{D(\text{kN})S(\frac{km}{h})}{3.6} \)Ecuación\(\PageIndex{15}\))
\( P_{d}=\frac{27.4(\text{kN})8(\frac{km}{h})}{3.6} = 60.89 \text{ kW} \)
Ejemplo\(\PageIndex{6}\)
Ejemplo 6: Pérdida de materia seca
Problema:
Una pila de pacas redondas del Ejemplo 1.4.5 deben almacenarse con un contenido promedio de humedad del 15% (base de masa húmeda). Estimar la pérdida de materia seca de las pacas cuando se cubren con lona y se almacenan en el suelo durante 9 meses y 18 meses.
Solución
La masa húmeda de la bala es de 866.5 kg (calculada en el Ejemplo 1.4.5). Calcule la masa seca de la paca usando el contenido de humedad promedio dado del 15% (base de masa húmeda):
\( \text{Bale dry mass} = 866.5 \times (1-0.15)=736.53 \text{ kg} \)
Asumir una pérdida de materia seca de rango medio de la Tabla 1.4.6, o porcentaje de masa seca de 7.5% durante 9 meses y 12.5% por 18 meses. Utilice los valores de porcentaje de pérdida de masa seca para calcular la pérdida de materia seca:
\( \text{Dry matter loss after 9 months} = 736.53 \times (0.075)=55.2 \text{ kg} \)
\( \text{Dry matter loss after 18 months} = 736.53 \times (0.125)=92.1 \text{ kg} \)
Créditos de imagen
Figura 1. Krone. (CC por 4.0). (2020). Ilustración de una paja de procesamiento de empacadora cuadrada. Usado con permiso por escrito. Recuperado de https://www.krone-northamerica.com/.
Figura 2. Krone. (CC por 4.0). (2020). Operación de empacadora cuadrada en línea. Usado con permiso por escrito. Recuperado de https://www.krone-northamerica.com/.
Figura 3. Sokhansanj, S. (CC por 4.0). (2020). Una parcela experimental de potencia en una empacadora cuadrada.
Figura 4. Krone. (CC por 4.0). (2020). La empacadora redonda hace una paca cilíndrica. Usado con permiso por escrito. Recuperado de https://www.krone-northamerica.com/.
Figura 5. Freeland y Bledsoe. (CC Por 1.0). (1988). Los dos tipos de empacadoras redondas. Recuperado de la publicación ASABE Transacciones.
Figura 6. Sokhansanj, S. (CC Por 4.0). (2020). Potencia medida para formar pacas redondas.
Figura 7. Ejemplos de apilamiento de pacas cuadradas grandes y pacas redondas. Foto de bala cuadrada adaptada de fondo removida: Cortesía de Ryley Schmidt, Barr-Ag Inc. Alberta. Foto de pacas redondas crédito: Evelyn Simak/Una pila de pacas de paja/CC BY-SA 2.0. (los detalles de la licencia se pueden encontrar aquí: https://commons.wikimedia.org/wiki/File:A_stack_of_straw_bales_-_geograph.org.uk_-_1501535.jpg)
Referencias
Afzalinia, S., & Roberge, M. (2013). Modelado de la relación presión-densidad en una empacadora cúbica grande. J. Agric. Sci. Tecnol. , 15 (1), 35-44.
Normas ASABE. (2015a). ASAE D497.7 MAR2011 (R2015): Datos de manejo de maquinaria agrícola. San José, MI: ASABE. http://elibrary.asabe.org
Normas ASABE. (2015b). ASAE EP496.3 FEB2006 (R2015) Cor.1: Manejo de Maquinaria Agrícola St. Joseph, MI: ASABE. http://elibrary.asabe.org
Estándares ASABE. (2018). ANSI/ASAE S296.5 DEC2003 (R2018): Terminología general para la tracción de dispositivos y vehículos agrícolas de tracción y transporte. San José, MI: ASABE. http://elibrary.asabe.org
Freeland, R. S., & Bledsoe, B. L. (1988). Energía requerida para formar grandes balas redondas de heno: efecto del procedimiento operativo y tipo de cámara de empacadora. Trans. ASAE, 31 (1), 63-67. http://dx.doi.org/10.13031/2013.30666.
Hofstetter, D. W., & Liu, J. (2011). Requisito de energía y consumo de energía de compresión de pacas. ASABE Papel No. 1111266, San José, MI: ASABE.
HSE (2012). Trabajo seguro con pacas en la agricultura. El Ejecutivo de Salud y Seguridad 05/12 INDG125 (rev3). 10 paginas. Recuperado de https://www.hse.gov.uk/pubns/indg125.pdf.
Kemmerer, B., & Liu, J. (2011). Eficacia de empacado cuadrado grande y manejo de pacas: un estudio de caso. Agric. Sci. , 3 (2), 178-183. http://dx.doi.org/10.4236/as.2012.32020.
Lemus, R. (2009). Almacenamiento de heno: Pérdidas de materia seca y cambios de calidad. Recuperado de http://pss.uvm.edu/pdpforage/Materials/CuttingMgt/Hay_Storage_DM_Losses_MissSt.pdf.
PAMI (1992). Informe de evaluación 677. Empacadora redonda John Deere 535. Recuperado de http://pami.ca/pdfs/reports_research_updates/(4a)%20Balers%20and%20Baler%20Attachments/677.PDF.
PAMI (1990). Informe de evaluación 628. Empacadora cuadrada Vicon MP800. Recuperado de http://pami.ca/pdfs/reports_research_updates/(4a)%20Balers%20and%20Baler%20Attachments/628.PDF.
Shinners, K., & Friede, J. (2018). Requerimientos energéticos para la cosecha y densificación de biomasa. Energías, 11 (4), 780. http://doi.org/10.3390/en11040780.
Tremblay, D., Saboya, P., & Lepha, Q. (1997). Requisitos de potencia y características de la bala para una empacadora de cámara fija y otra de cámara variable. Canadiense Agric. Ing. , 39 (1), 73-75. Recuperado de https://pdfs.semanticscholar.org/cb81/3812beeb7dcee3ecd34e5dbf39617869b8a6.pdf.
Van Pelt, T. (2003). Densificación de biomasa de maíz, soya y alfalfa. Agric. Ing. Intl. Manuscrito EE 03 002. Recuperado de https://pdfs.semanticscholar.org/8d9f/46c0431869b9f2b8edbedb4fcc5e657b7ac2.pdf.
Wilcke, W., Cuomo, G., Martinson, K., & Fox, C. (2018). Preservar el valor del heno seco almacenado. Recuperado de https://extension.umn.edu/forage-harvest-and-storage/preserving-value-dry-stored-hay.


