2.3: Procesamiento de Datos en Ingeniería de Biosystems

Introducción

Las nuevas tecnologías de detección y procesamiento de datos juegan un papel muy importante en la mayoría de los escenarios en las amplias variedades de aplicaciones de ingeniería de biosistemas, como el control y monitoreo ambiental, el procesamiento de alimentos y control de seguridad, el diseño de maquinaria agrícola y su automatización, y la biomasa y producción de bioenergía, particularmente en la era del big data. Por ejemplo, para lograr una clasificación automática y no destructiva de los productos agrícolas de acuerdo con sus propiedades físicas y químicas, se deben adquirir datos brutos de diferentes tipos de sensores y procesarse cuidadosamente para describir con precisión las muestras de manera que los productos puedan clasificarse en diferentes categorías correctamente (Gowen et al., 2007; Feng et al., 2013; O'Donnell et al., 2014; Baietto y Wilson, 2015; Park y Lu, 2016). Para el control ambiental de los invernaderos, la temperatura, la humedad y la concentración de gases particulares deben determinarse procesando los datos brutos adquiridos de termistores, hidrómetros y narices electrónicas o sensores ópticos (Bai et al., 2018). El uso exitoso de las mediciones depende en gran medida del procesamiento de datos que convierte los datos sin procesar en información significativa para facilitar la interpretación y comprensión de los objetivos de interés.

El propósito del procesamiento de datos es convertir los datos sin procesar en información útil que pueda ayudar a comprender la naturaleza de los objetos o un proceso. Para que todo este procedimiento sea exitoso, se debe prestar especial atención para garantizar la calidad de los datos brutos. Sin embargo, los datos brutos obtenidos de los sistemas biológicos siempre se ven afectados por factores ambientales y el estado de las muestras. Por ejemplo, los perfiles ópticos de la carne son vulnerables a la variación de temperatura, condiciones de luz, razas, edad y sexo de los animales, tipo de alimento, origen geográfico, entre otros factores. Para garantizar la mejor calidad de los datos sin procesar, el pretratamiento de los datos es esencial.

En este capítulo, se introducen métodos de pretratamiento de datos, incluyendo suavizado, derivados y normalización. Con datos de buena calidad, se puede desarrollar un proceso de modelado que correlacione los datos brutos con características del objeto o proceso de interés. Esto se puede realizar empleando diferentes métodos de modelado. Después de la validación, el modelo establecido puede ser utilizado para aplicaciones reales.

Resultados

Después de leer este capítulo, deberías poder:

• Describir los principios de diversos métodos de procesamiento de datos
• Determinar métodos de procesamiento de datos apropiados para el desarrollo de modelos
• Evaluar el desempeño de los modelos establecidos
• Enumerar ejemplos de la aplicación del tratamiento de datos

Conceptos

Pretratamiento de datos

Suavizado de datos

Para comprender las características de los objetos biológicos, se pueden emplear diferentes sensores o instrumentos para adquirir señales que representen sus propiedades. Por ejemplo, se utiliza un espectrómetro de infrarrojo cercano (NIR) para recolectar las propiedades ópticas a través de diferentes longitudes de onda, llamadas espectro, de un producto alimenticio o agrícola. Sin embargo, durante la adquisición de señal (es decir, espectro), inevitablemente se introducirá ruido aleatorio, lo que puede deteriorar la calidad de la señal. Por ejemplo, las fluctuaciones a corto plazo pueden estar presentes en las señales, lo que puede deberse a efectos ambientales, como la respuesta de corriente oscura y el ruido de lectura del instrumento. La corriente oscura está compuesta por electrones producidos por variaciones de energía térmica, y el ruido de lectura se refiere a la información derivada del funcionamiento imperfecto de los dispositivos electrónicos. Ninguno de ellos contribuye a la comprensión de los objetos investigados. Para disminuir tales efectos, se suele aplicar suavizado de datos. Algunos métodos populares de suavizado de datos incluyen el suavizado de promedio móvil (MV) y S-G (Savitzky y Golay).

La idea de la media móvil es aplicar “ventanas correderas” para suavizar ruidos aleatorios en cada segmento de la señal calculando el valor promedio en el segmento para que se pueda reducir el ruido aleatorio en toda la señal. Dada una ventana con un número par de puntos de datos en una determinada posición, se calcula el valor promedio de los datos originales dentro de la ventana y se utiliza como el nuevo valor suavizado para la posición del punto central. Este procedimiento se repite hasta llegar al final de la señal original. Para los puntos de datos en los dos bordes de la señal que no pueden ser cubiertos por una ventana completa, todavía se puede suponer que se aplica la ventana pero solo se calcula el promedio de los datos disponibles en la ventana. El ancho de la ventana es un factor clave que debe determinarse cuidadosamente. No siempre es cierto que la relación señal/ruido aumenta con el ancho de la ventana, ya que una ventana demasiado grande tenderá a suavizar la señal útil también. Además, dado que el valor promedio se calcula para cada ventana, todos los puntos de datos en la ventana se consideran contribuyentes iguales para la señal; esto a veces resultará en distorsión de la señal. Para evitar este problema, se puede introducir el suavizado S-G.

En lugar de utilizar un promedio simple en el proceso de media móvil, Savitzky y Golay (1964) propusieron asignar pesos a diferentes datos en la ventana. Dada una señal X original, la señal suavizada XS se puede obtener como:

\[ XS_{i}=\frac{\sum^{r}_{j=-r} X_{i+j}W_{j}}{\sum{^{r}_{j=-r}W_{j}}} \]

donde 2 r + 1 es ancho de ventana y W _i es el peso para el punto de datos ^i-ésimo en la ventana. W se obtiene ajustando los puntos de datos en la ventana a una forma polinómica siguiendo el principio de mínimos cuadrados para minimizar los errores entre la señal original X y la señal suavizada XS y calculando los puntos centrales de la ventana a partir del polinomio. Al aplicar el suavizado S-G, primero deben decidirse los puntos de suavizado y el orden de los polinomios. Una vez determinados los dos parámetros, los coeficientes de ponderación se pueden aplicar entonces a los puntos de datos en la ventana para calcular el valor del punto central mediante la Ecuación 2.3.1.

La Figura 2.3.1 muestra el efecto suavizante aplicando el alisado S-G a un espectro de muestra de carne de res (Figura 2.3.1b-d). Se muestra claramente que después del suavizado S-G, el ruido aleatorio en la señal original (Figura 2.3.1a) se suprime en gran medida cuando el ancho de la ventana es 3 (Figura 2.3.1b). Se logra un resultado aún mejor cuando el ancho de ventana aumenta a 5 y 7, donde la curva se vuelve más suave (Figura 2.3.1d) y apenas se ven las fluctuaciones cortas.

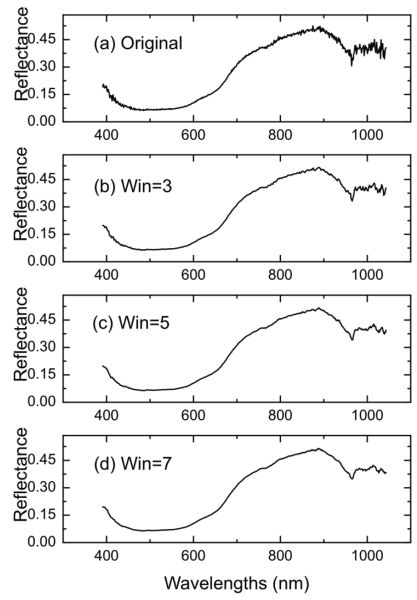
Gráficos de cuatro líneas que representan el suavizado Savitzky y Golay de las señales espectrales. Respectivamente, las gráficas trazan el espectro original y el espectro con anchos de ventana de tres, cinco y siete. — Figura\(\PageIndex{1}\): Alisado S-G de una señal espectral. (a) El espectro original; (b), (c) y (d) son resultados de suavizado S-G bajo anchos de ventana (Win) de 3, 5 y 7, respectivamente.

Derivados

Los derivados son métodos para recuperar información útil a partir de datos mientras se eliminan cambios lentos de señales (o señales de baja frecuencia) que podrían ser inútiles para determinar las propiedades de las muestras biológicas. Por ejemplo, para un espectro definido como una función y = f (x), la primera y segunda derivadas se pueden calcular como:

\[ \frac{dy}{dx} = \frac{f(x+\Delta x)-f(x)}{\Delta x} \]

A partir de las Ecuaciones 2.3.2 y 2.3.3, se puede entender que el desplazamiento (por ejemplo, desplazamiento constante de señales) de la señal puede eliminarse después del procesamiento de la primera derivada, mientras que tanto el desplazamiento como la pendiente en la señal original pueden excluirse después del procesamiento de la segunda derivada. Específicamente, para la primera derivada, los valores constantes (correspondientes al desplazamiento) pueden eliminarse debido a la operación de diferencia en el numerador de la Ecuación 2.3.2. Después de la primera derivada, la curva espectral con la misma pendiente se puede convertir en un nuevo desplazamiento y esto puede ser eliminado adicionalmente por una segunda derivada. Dado que las variaciones de desplazamiento y la información de pendiente siempre indican efectos ambientales sobre la señal y factores irrelevantes que están estrechamente correlacionados con variables independientes, la aplicación de métodos derivados ayudará a reducir dichos ruidos. Además, el procesamiento de señales con derivados ofrece un enfoque eficiente para mejorar la resolución de las señales al descubrir más picos, particularmente en el análisis espectral.

Para muestras biológicas con componentes químicos complicados, los espectros son normalmente la combinación de diferentes picos de absorbancia que surgen de estos componentes. Dichos picos superpuestos, sin embargo, pueden estar bien separados en espectros de segunda derivada. Sin embargo, cabe señalar que la relación señal-ruido de la señal se deteriorará con el aumento de los órdenes derivados, ya que el ruido también se mejora sustancialmente, particularmente para las derivadas de orden superior, aunque a veces se encuentra que las derivadas de orden alto son útiles para comprender la propiedades detalladas de los objetos. Para evitar la mejora del ruido, se puede introducir una derivada S-G donde se obtienen derivadas de señal calculando las derivadas del polinomio. Específicamente, los puntos de datos en una ventana deslizante se ajustan a un polinomio de cierto orden siguiendo el procedimiento de suavizado S-G. Dentro de la ventana, luego se calculan las derivadas del polinomio ajustado para producir nuevos pesos para el punto central. Cuando la ventana deslizante alcanza el final de la señal, se obtienen entonces derivadas de la señal de corriente.

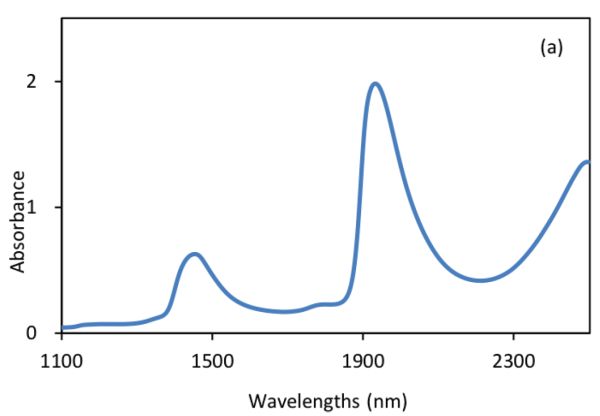
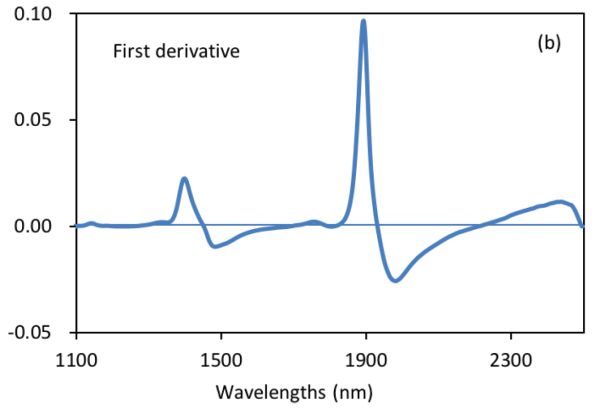
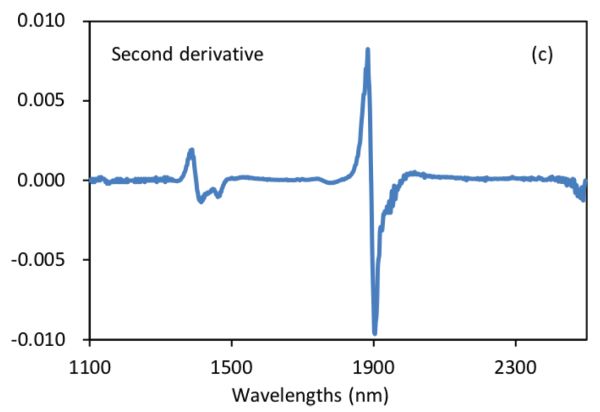
La Figura 2.3.2 muestra los espectros de absorbancia y derivados de suspensiones bacterianas (Feng et al., 2015). Se demuestra que después de la operación derivada S-G con 5 puntos de alisado y orden polinomial de 2, el desplazamiento constante y el desplazamiento de línea base lineal en el espectro original (Figura 2.3.2a) se eliminan efectivamente en los espectros derivados primero (Figura 2.3.2b) y segundo (Figura 2.3.2c), respectivamente. Particularmente, la segunda técnica derivada también es una herramienta útil para separar picos superpuestos donde un pico a ~1450 nm se resuelve en dos picos a 1412 y 1462 nm.

Un gráfico lineal que muestra los espectros derivados del infrarrojo cercano de suspensiones bacterianas en el espectro original.

Un gráfico lineal que muestra los espectros derivados del infrarrojo cercano de suspensiones bacterianas en el espectro de la primera derivada.

Un gráfico lineal que muestra los espectros derivados del infrarrojo cercano de suspensiones bacterianas en el espectro de la segunda derivada. — Figura\(\PageIndex{2}\): Espectros de derivados NIR de suspensiones bacterianas. (a): espectro original; (b): Espectro de primera derivada; (c) espectro de segunda derivada.

Normalización

El propósito de la normalización de datos es igualar la magnitud de las señales de muestra para que todas las variables de una muestra puedan ser tratadas por igual para su posterior análisis. Por ejemplo, la temperatura superficial de los cerdos y los factores ambientales (temperatura, humedad y velocidad del aire) se pueden combinar para detectar la temperatura rectal de las cerdas. Dado que los valores para la temperatura de la superficie del cerdo pueden estar alrededor de 39°C, mientras que la velocidad del aire está mayormente por debajo de 2 m/s, si estos valores se usan directamente para análisis de datos adicionales, la temperatura de la superficie desempeñará intrínsecamente un papel más dominante que la velocidad del aire simplemente debido a sus valores mayores. Esto puede conducir a una interpretación sesgada de la importancia de las variables. La normalización de datos también es útil cuando las señales de diferentes sensores se combinan como variables (es decir, fusión de datos) para caracterizar muestras biológicas de composición compleja y fácilmente afectadas por las condiciones ambientales. Sin embargo, dado que la normalización de los datos elimina el promedio así como la desviación estándar de las variables de la muestra, podría dar información confusa sobre las muestras si las variabilidades de las variables en diferentes unidades son importantes para caracterizar las propiedades de la muestra.

La variación normal estándar (SNV), o estandarización, es uno de los métodos más populares utilizados para normalizar los datos de la muestra (Dhanoa et al., 1994). Dado un dato de muestra X, el X normalizado _ni se puede obtener como:

\[ X_{nor}=\frac{X-mean(X)}{SD(X)} \]

donde media (X) y SD (X) son la media y desviación estándar de X, respectivamente.

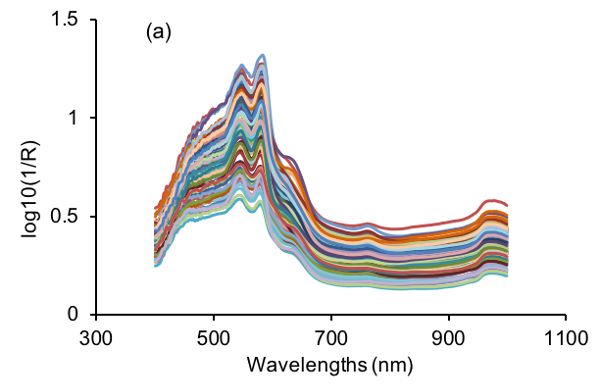
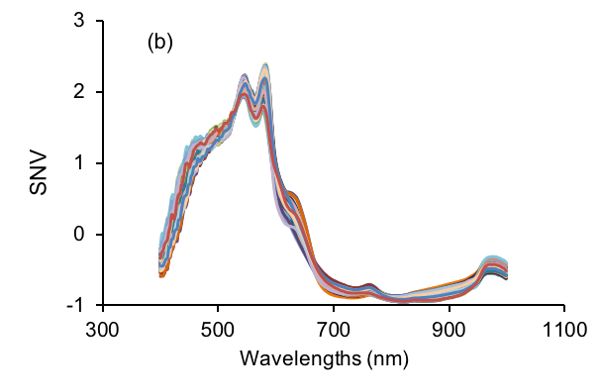
Después de la transformación SNV, se produce una nueva señal con un valor medio de 0 y desviación estándar unitaria. Por lo tanto, el SNV es útil para eliminar la varianza dimensional entre variables ya que todas las variables se comparan al mismo nivel. Además, como se muestra en la Figura 2.3.3, el SNV es capaz de corregir el efecto de dispersión de las muestras debido a la estructura física de las muestras durante las interacciones luz-materia (Feng y Sun, 2013). Específicamente, las grandes variaciones en los espectros NIR visibles (vis-NIR) de muestras de carne de res (Figura 2.3.3a) se suprimen sustancialmente como se muestra en la Figura 2.3.3b.

Métodos de Modelado

El propósito del modelado en el procesamiento de datos es principalmente establecer la relación entre variables independientes y variables dependientes. Las variables independientes se definen como factores independientes que pueden ser utilizados para determinar los valores de otras variables. Dado que los valores de otras variables dependen de las variables independientes, se denominan variables dependientes. Por ejemplo, si el tamaño, el peso y el color se utilizan para clasificar las manzanas en diferentes grados, las variables de tamaño, peso y color son las variables independientes y el grado de las manzanas es la variable dependiente. Las variables dependientes se calculan a partir de variables independientes medidas. Durante el desarrollo del modelo, si solo se usa una variable independiente, el modelo resultante es un modelo univariado, mientras que dos o más variables independientes están involucradas en modelos multivariados. Si se utilizan variables dependientes durante la calibración o entrenamiento del modelo, los métodos aplicados en el desarrollo del modelo se llaman supervisados. De lo contrario, se emplea un método no supervisado. El conjunto de datos utilizado para el desarrollo del modelo se denomina conjunto de calibración (o conjunto de entrenamiento) y un nuevo conjunto de datos donde se aplica el modelo para la validación es el conjunto de validación (o conjunto de predicción).

Un gráfico lineal de las variaciones en los espectros de infrarrojo cercano original y visible de muestras de carne adulterada con carne de pollo.

Un gráfico lineal de las variaciones en los espectros estándar de variados normales procesados y visibles del infrarrojo cercano de muestras de carne adulterada con carne de pollo. — Figura\(\PageIndex{3}\): Procesamiento SNV de espectros Vis-NIR de muestras de carne adulterada con carne de pollo. (a) Espectros originales; (b) Espectros procesados SNV.

Los modelos desarrollados pueden ser utilizados para diferentes propósitos. Básicamente, si el modelo se usa para predecir una clase discreta (categórica), es un modelo de clasificación; y si pretende predecir una cantidad continua, es un modelo de regresión. Por ejemplo, si se utilizan espectros de muestras para identificar los orígenes geográficos de la carne de res, los espectros (propiedades ópticas a diferentes longitudes de onda) son las variables independientes y los orígenes geográficos son las variables dependientes. El modelo multivariado establecido que describe la relación entre espectros y orígenes geográficos es un modelo de clasificación. En un modelo de clasificación, las variables dependientes son variables ficticias (o etiquetas) donde se utilizan diferentes números arbitrarios para representar diferentes clases pero sin significado físico. Por otro lado, si se utilizan espectros de muestras para determinar el contenido de agua de la carne de res, el modelo desarrollado es entonces un modelo de regresión. Las variables dependientes son números significativos que indican el contenido real de agua. Simplemente, un modelo de clasificación trata de responder a la pregunta de “¿Qué es?” y un modelo de regresión intenta determinar “¿Cuánto hay?” Existe una amplia gama de métodos para modelos de regresión o clasificación. Algunos se describen a continuación.

Regresión lineal

La regresión lineal es un método analítico que explora la relación lineal entre variables independientes (X) y variables dependientes (Y). La regresión lineal simple se utiliza para establecer el modelo más simple que se puede utilizar para ilustrar la relación entre una variable independiente X y una variable dependiente Y. El modelo puede describirse como:

\[ y = \beta_{0}+\beta_{1}X+E \]

donde X es la variable independiente; Y es la variable dependiente;\(\beta_{0}\),\(\beta_{1}\), son los coeficientes de regresión; y E es el vector residual.

La regresión lineal simple se utiliza cuando solo una variable independiente debe correlacionarse con la variable dependiente. En el modelo, los dos coeficientes importantes,\(\(\beta_{0}\) y\(\beta_{1}\), se pueden determinar encontrando la línea de mejor ajuste a través de la curva de dispersión entre X e Y mediante el método de mínimos cuadrados. La línea de mejor ajuste requiere la minimización de errores entre la Y real y la predicha\(\hat{Y}\). Dado que los errores podrían ser positivos o negativos, es más apropiado usar la suma de errores al cuadrado. En base a esto,\(\beta_{0}\) y se\(\beta_{1}\) puede calcular como:

\[ \beta_{1}=\frac{\sum^{n}_{i=1}(X_{i}-\bar{X})(Y_{i}-\bar{Y})}{\sum^{n}_{i=1}(X_{i}-\bar{X})^{2}} \]

\[ \beta_{0}=\bar{Y}-\beta_{1}\bar{X} \]

donde\(\bar{X}\) y\(\bar{Y}\) son valores medios de X e Y, respectivamente, y n es el número de muestras.

La regresión lineal múltiple (MLR) es un método de análisis lineal para regresión en el que se establece el modelo correspondiente entre múltiples variables independientes y una variable dependiente (Ganesh, 2010):

\[ Y=\beta_{0}+\sum^{n}_{j=i}\beta_{j}X_{j}+E \]

donde\(X_{j}\) es la variable\(j^{th}\) independiente; Y es la variable dependiente;\(\beta_{0}\) es la intercepción;\(\beta_{1}\)\(\beta_{2}\),,. ,\(\beta_{n}\) son coeficientes de regresión y E es la matriz residual.

Aunque la MLR tiende a dar mejores resultados en comparación con la regresión lineal simple ya que se utilizan más variables, la MLR solo es adecuada para situaciones en las que el número de variables es menor que el número de muestras. Si el número de variables excede el número de muestras, la Ecuación 2.3.8 quedará subdeterminada y se podrán producir infinitas soluciones para minimizar los residuos. Por lo tanto, la regresión lineal múltiple generalmente se emplea en base a variables características importantes (como longitudes de onda importantes en el análisis espectral) en lugar de todas las variables, si el número de variables es mayor que el de las muestras.

Similar a la regresión lineal simple, la determinación de los coeficientes de regresión también se basa en la minimización de los residuos de predicción (es decir, la suma de los residuos cuadrados entre los valores Y verdaderos y los predichos\(\hat{Y}\)). Los procedimientos específicos se pueden encontrar en otros lugares (Friedman et al., 2001).

Análisis de componentes principales (PCA)

Debido a la naturaleza complicada de las muestras biológicas, los datos adquiridos para caracterizar muestras suelen involucrar muchas variables. Por ejemplo, se pueden usar respuestas espectrales a cientos a miles de longitudes de onda para caracterizar los componentes físicos y químicos de las muestras. Tal gran dimensionalidad trae inevitablemente dificultades en la interpretación de los datos. Con los datos multivariados originales, cada variable independiente o combinaciones de variables se pueden utilizar para dibujar gráficas de una, dos o tridimensionales para comprender la distribución de las muestras. Sin embargo, este proceso requiere una enorme carga de trabajo y es poco realista si están involucradas más de tres variables.

El análisis de componentes principales (PCA) es una poderosa herramienta para comprimir datos y proporciona una forma mucho más eficiente de visualizar la estructura de datos. La idea de PCA es encontrar un conjunto de nuevas variables que no estén correlacionadas entre sí y adjuntar la mayor cantidad de información de datos a las primeras variables (Hotelling, 1933). Inicialmente, PCA intenta encontrar la mejor coordenada que pueda representar la mayor cantidad de variaciones de datos en los datos originales y registrarla como PC1. Posteriormente se extraen otras PC para cubrir las mayores variaciones de los datos restantes. El modelo de PCA establecido se puede expresar como:

\[ X=TP^{T}+E \]

donde X es la matriz variable independiente, T es la matriz de puntuación, P ^T es la matriz de carga y E es la matriz residual. La matriz de puntuación se puede utilizar para visualizar la relación entre muestras y las cargas se pueden utilizar para expresar las relaciones entre variables.

Después de PCA, los datos pueden ser representados por unas pocas PC (generalmente menos de 10). Estas PC se clasifican de acuerdo a su contribución a la explicación de la varianza de datos. Específicamente, se suele emplear una tasa de contribución acumulada, definida como varianza explicada de los primeros PC sobre la varianza total de los datos, para evaluar cuántas variables nuevas (PC) deben usarse para representar los datos. Sin embargo, al aplicar PCA, se reduce sustancialmente el número de variables requeridas para caracterizar la varianza de los datos. Después de proyectar los datos originales en los nuevos espacios de PC, la estructura de datos se puede ver fácilmente, si existe.

Regresión de mínimos cuadrados parciales (PLSR)

Como se ilustra anteriormente, MLR requiere que el número de muestras sea mayor que el número de variables. Sin embargo, los datos biológicos normalmente contienen muchas más variables que las muestras, y algunas de estas variables pueden estar correlacionadas entre sí, proporcionando información redundante. Para hacer frente a este dilema, la regresión de mínimos cuadrados parciales (PLSR) puede ser utilizada para reducir el número de variables en los datos originales conservando la mayor parte de su información y eliminando variaciones redundantes (Mevik et al., 2011). En PLSR, tanto X como Y se proyectan a nuevos espacios. En tales espacios, la dirección multidimensional de X se determina para dar cuenta mejor de la mayor varianza de la dirección multidimensional de Y. En otras palabras, PLSR descompone tanto los predictores X como la variable dependiente Y en combinaciones de nuevas variables (puntuaciones) asegurando la correlación máxima entre X e Y (Geladi y Kowalski, 1986). Específicamente, la puntuación T de X se correlaciona con Y usando las siguientes fórmulas:

\[ Y= XB+ E=XW^{*}_{a}C+E=TC+E \]

\[ W^{*}_{a}=W_{a}(P^{T}W_{a})^{-1} \]

donde B son los coeficientes de regresión para el modelo PLSR establecidos; E es la matriz residual; W _a representa los pesos PLS; a es el número deseado de nuevas variables adoptadas; P y C son cargas para X e Y, respectivamente. Las nuevas variables adoptadas suelen denominarse como variables latentes (LV) ya que no son las variables independientes observadas sino que se deducen de ellas.

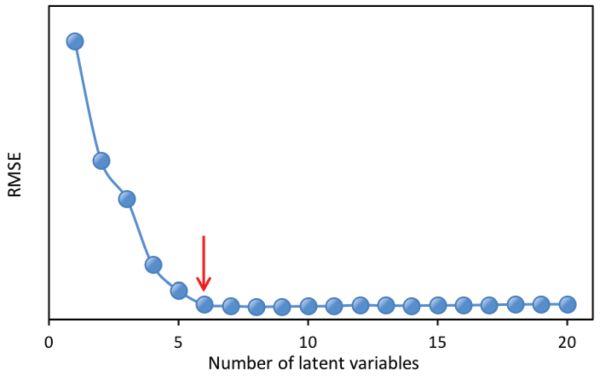
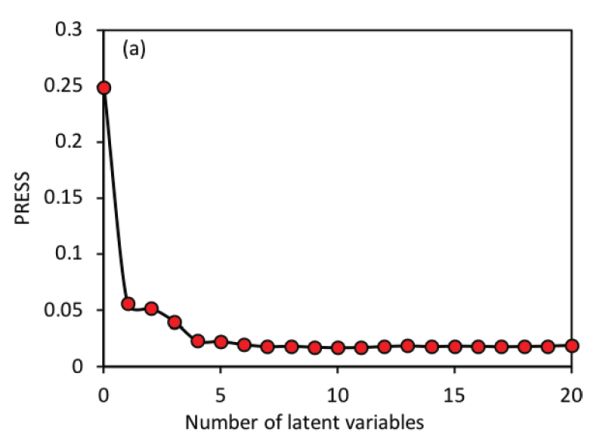
El parámetro más importante en la regresión PLS es la determinación del número de LV. Con base en los modelos PLSR establecidos con diferentes LVs, se utiliza comúnmente un método llamado validación cruzada dejar-uno-out para validar los modelos. Es decir, para el modelo con cierto número de LVs, se deja fuera una muestra del conjunto de datos con las muestras restantes utilizadas para construir un nuevo modelo. Luego se aplica el nuevo modelo a la muestra que se deja fuera para predicción. Este procedimiento se repite hasta que cada muestra haya quedado fuera una vez. Finalmente, cada muestra tendría dos valores, es decir, el valor verdadero y el valor predicho. Estos dos tipos de valores se pueden usar para calcular errores cuadráticos medios de raíz (RMSes; Ecuación 2.3.13 en la sección Evaluación del modelo a continuación) para diferentes números de LVs. Por lo general, el número óptimo de LV se determina ya sea en el valor mínimo de RMSE o aquel después del cual los RMSE no son significativamente diferentes del RMSE mínimo. En la Figura 2.3.4 por ejemplo, el uso de 6 variables latentes produciría un valor RMSE muy similar al mínimo RMSE que se alcanza con 11 LVs; por lo tanto, 6 variables latentes serían más adecuadas para un desarrollo de modelos más simples.

Un gráfico de líneas que traza el error cuadrático medio raíz en función del número de variables latentes. — Figura\(\PageIndex{4}\): Gráfica del error cuadrático medio (RMSE) en función del número de variables latentes (LVs) para un modelo PLSR. La RMSE mínima se alcanza cuando se utilizan 11 variables latentes. Sin embargo, usar 6 LVs, como lo indica la flecha roja, es mejor en términos de simplicidad del modelo.

Además de los métodos introducidos anteriormente, hay muchos más algoritmos disponibles para el desarrollo de modelos. Con el rápido crecimiento de la informática y las tecnologías de la información, los métodos modernos de aprendizaje automático, que incluyen redes neuronales artificiales, aprendizaje profundo, árboles de decisión y máquinas de vectores de soporte, son ampliamente utilizados en la ingeniería de biosistemas (LeCun et al., 2015; Maione y Barbosa, 2019; Pham et al., 2019, Zhao et al., 2019).

Los métodos de desarrollo de modelos descritos anteriormente pueden ser utilizados tanto para problemas de regresión como de clasificación. Para la regresión, los resultados finales son los resultados producidos cuando las variables independientes son ingresadas en los modelos establecidos. Para la clasificación, se requiere una operación adicional para alcanzar los números finales para la representación categórica. Normalmente, se adopta una operación de redondeo. Por ejemplo, una salida directa de 1.1 del modelo tiende a redondearse a 1 como resultado final, que puede ser una etiqueta para una determinada clase. Después de dicha modificación, el nombre del método de regresión puede cambiarse de PLSR a análisis discriminante de mínimos cuadrados parciales (PLS-DA), como ejemplo. Sin embargo, estos números no tienen significados físicos reales y, por lo tanto, a menudo se les denomina variables ficticias.

Dado que un modelo se puede establecer utilizando diferentes métodos de modelado, algunos de los cuales se describen anteriormente, la decisión sobre qué tipo de método usar es específica de la tarea. Si el objetivo es lograr un modelo estable con alta precisión, se debe emplear el que pueda conducir al mejor rendimiento del modelo. Sin embargo, si la principal preocupación es la simplicidad y la fácil interpretación basada en una aplicación factible, un método lineal suele ser la mejor opción. En los casos en que un modelo lineal no logra representar la correlación entre X e Y, entonces podrían aplicarse modelos no lineales establecidos mediante la aplicación de redes neuronales artificiales o máquinas de vectores de soporte.

Evaluación de modelos

El proceso completo de desarrollo de modelos incluye la calibración, validación y evaluación de modelos. La calibración del modelo intenta emplear diferentes métodos de modelado a los datos de entrenamiento para encontrar los mejores parámetros para la representación de muestras. Por ejemplo, si se aplica PLSR a datos espectrales NIR para cuantificar la adulteración de carne de res con carne de cerdo, se determinan los parámetros importantes que incluyen el número de LV y los coeficientes de regresión para que cuando se ingresen los espectros al modelo, se pueda calcular el porcentaje previsto de niveles de adulteración. Es claro que este proceso simplemente funciona sobre los datos de entrenamiento en sí y el modelo resultante puede explicar mejor los datos de las muestras particulares. Sin embargo, dado que el proceso de modelado es específico de datos, un buen rendimiento del modelo a veces puede deberse al modelado del ruido y dichos modelos no funcionarán con datos nuevos e independientes. Este problema se conoce como sobreajuste y siempre debe evitarse durante el modelado. Por lo tanto, es de crucial importancia validar el desempeño de los modelos utilizando datos independientes, es decir, datos que no están incluidos en el conjunto de calibración y que son totalmente desconocidos para el modelo establecido.

La validación del modelo es un proceso para verificar si se puede lograr un rendimiento del modelo similar al de la calibración. Básicamente hay dos formas de llevar a cabo la validación del modelo. Una es usar la validación cruzada, si no hay suficientes muestras disponibles. La validación cruzada se implementa en base al conjunto de entrenamiento y a menudo se toma un enfoque de dejar uno fuera (Klanke y Ritter, 2006). Durante la validación cruzada sin dejar uno, se deja una muestra fuera del conjunto de calibración y se desarrolla un modelo de calibración basado en los datos restantes. La muestra sobrante se introduce luego en el modelo desarrollado en base a las otras muestras. Este procedimiento termina cuando se han omitido todas las muestras una vez. Finalmente, todas las muestras serán predichas para su comparación con los valores medidos. Sin embargo, este método se debe utilizar con precaución ya que puede llevar a una evaluación sobreoptimista o a un sobreajuste del modelo. Otro enfoque, llamado validación externa, es introducir un conjunto de predicción independiente que no esté incluido en el conjunto de calibración y aplicar el modelo al nuevo conjunto de datos independiente. Siempre se prefiere la validación externa para la evaluación del modelo. Sin embargo, se recomienda aplicar métodos tanto de validación cruzada como de validación externa para evaluar el desempeño de los modelos. Esto es particularmente importante en la ingeniería de biosistemas porque las muestras biológicas son muy complejas y sus propiedades pueden cambiar con el tiempo y el ambiente. Para las muestras de carne, los componentes químicos de la carne varían debido a las especies, orígenes geográficos, patrones de reproducción e incluso diferentes porciones del cuerpo del mismo tipo de animal. La atmósfera y temperatura del empaque también tienen gran influencia en las variaciones de calidad de la carne. Idealmente, con un modelo bueno y estable, los resultados de la validación cruzada y la validación externa deberían ser similares.

La evaluación del modelo es una parte indispensable del desarrollo del modelo, que tiene como objetivo determinar el mejor desempeño de un modelo así como verificar su validez para futuras aplicaciones calculando y comparando algunas estadísticas (Gauch et al., 2003). Para problemas de regresión, se calculan dos parámetros comunes, el coeficiente de determinación (^R2) y el error cuadrático medio (RMSE), para expresar el desempeño de un modelo. Se definen de la siguiente manera:

\[ R^{2} = 1- \frac{\sum^{n}_{i=1}(Y_{i,meas}-Y_{i,pre})^{2}}{\sum^{n}_{i=1}(\bar{Y}-Y_{i,pre})^{2}} \]

\[ \text{RMSE} = \sqrt{\frac{1}{n} \sum^{n}_{i=1}(Y_{i,meas}-Y_{i,pre})^{2}} \]

donde Y _{i, pre} e Y _{i, meas}, respectivamente, representan el valor predicho y el valor medido de dianas para la muestra i; es el valor objetivo medio para todas las muestras. Un R ² de 1 y RMSE de 0 para todos los conjuntos de datos indicaría un modelo “perfecto”. Así, el objetivo es tener R ² lo más cerca posible de 1 y RMSE cerca de 0. Además, un modelo estable tiene valores similares de ^R2 y RMSE para calibración y validación. Cabe señalar que R, la raíz cuadrada de ^R2, o coeficiente de correlación, también se utiliza frecuentemente para expresar la relación lineal entre los valores pronosticados y medidos. Además, dado que se pueden usar diferentes conjuntos de datos durante el desarrollo del modelo, los parámetros anteriores se pueden modificar de acuerdo. Por ejemplo, R ² _C, R ² _CV y R ² _P pueden usarse para representar los coeficientes de determinación para calibración, validación cruzada y predicción, respectivamente. Los errores cuadrados medios de raíz para calibración, validación cruzada y predicción se denotan como RMSEC, RMSECV y RMSEP, respectivamente.

Para problemas de clasificación, la tasa general de clasificación correcta (OCCR) de un modelo es un índice importante utilizado para evaluar el desempeño de la clasificación:

\[ \text{OCCR} = \frac{\text{Number of correctly classified samples}}{\text{Total number of samples}} \]

El número de muestras correctamente clasificadas se determina comparando la clasificación predicha con la clasificación conocida. Para investigar el desempeño detallado de la clasificación, se puede utilizar una matriz de confusión (Townsend, 1971). En el Cuadro 2.3.1 se muestra una matriz de confusión para las clasificaciones binarias. En la matriz de confusión, el verdadero positivo y el verdadero negativo indican muestras que se predicen correctamente. Falsos positivos y falsos negativos se encuentran cuando lo que no es cierto se considera erróneamente como verdadero y viceversa. Con base en la matriz de confusión, se pueden alcanzar parámetros para evaluar el modelo de clasificación, incluyendo la sensibilidad, especificidad y prevalencia, entre otros:

Cuadro\(\PageIndex{1}\): Matriz de confusión para clasificación binaria.
	Condición Positiva	Condición Negativa
Positivo pronosticado	Verdadero positivo (Poder)	Falso positivo (error tipo I)
Negativo pronosticado	Falso negativo (Error tipo Il)	Verdadero negativo

\[ \text{Sensitivity} = \frac{\sum \text{True positive}}{\sum \text{Condition positive}} \]

\[ \text{Specificity} = \frac{\sum \text{True negative}}{\sum \text{Condition negative}} \]

\[ \text{Prevalence} = \frac{\sum \text{Condition positive}}{\sum \text{Total positive}} \]

Aplicaciones

Detección de adulteración de carne

La adulteración alimentaria causa desconfianza en la industria alimentaria al provocar el desperdicio de alimentos debido a la recuperación de alimentos y la pérdida de confianza del consumidor. Por lo tanto, es crucial utilizar tecnologías modernas para detectar adulteración deliberada o contaminación accidental. Por ejemplo, se puede usar un espectrómetro de mano para obtener espectros de muestras de carne de res. Los espectros crudos pueden ser procesados por el espectrómetro para cuantificar el nivel, en su caso, de adulteración de cada muestra de carne de res. Para procesar adecuadamente los espectros brutos, se pueden usar experimentos de contaminación intencionados para determinar los métodos de pretratamiento (o preprocesamiento) apropiados para los datos brutos. Por ejemplo, la Figura 2.3.5a muestra espectros correspondientes a diferentes niveles de adulteración. La concentración de adulteración en dicho experimento debería oscilar entre 0% y 100%, siendo 0% carne fresca pura y 100% para carne pura en mal estado. El experimento debe incluir un conjunto de datos de calibración para desarrollar la relación predictiva a partir de espectros y un conjunto de datos independiente para probar la validez de la predicción. El siguiente proceso se puede utilizar para determinar el mejor método de preprocesamiento para la cuantificación de la adulteración de carne de res.

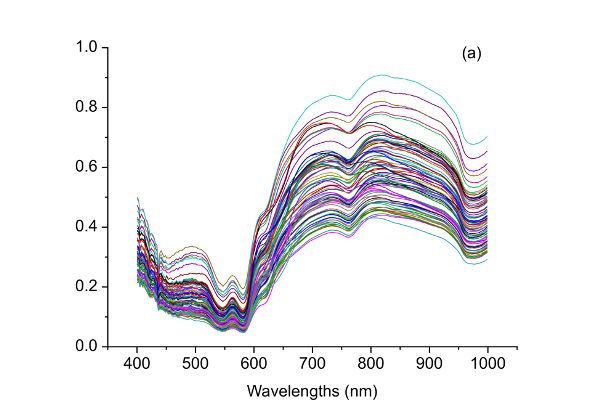
Un gráfico de líneas que muestra los espectros de carne cruda correspondientes a diferentes niveles de adulteración.

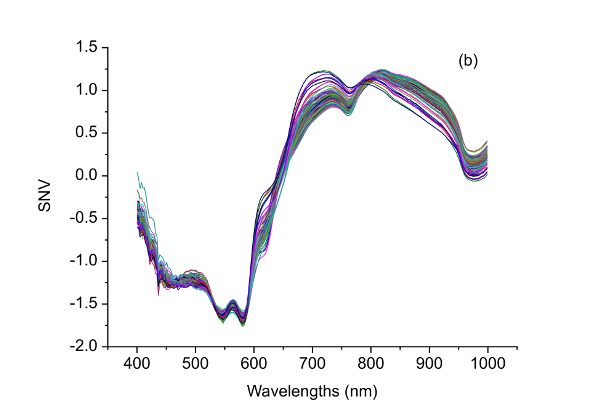
Un gráfico de líneas que muestra los espectros preprocesados de la variable normal estándar correspondientes a diferentes niveles de adulteración.

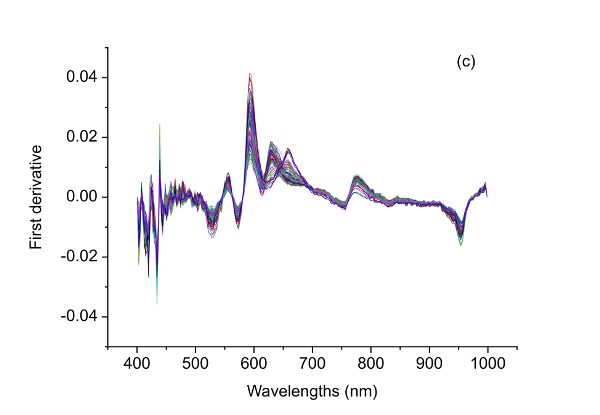
Un gráfico lineal que muestra los espectros preprocesados con primeras derivadas correspondientes a diferentes niveles de adulteración.

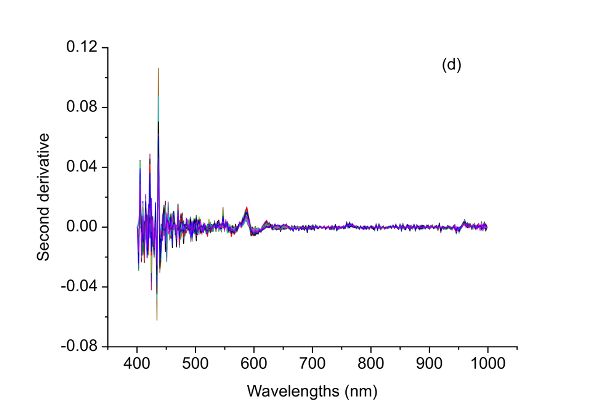
Un gráfico lineal que muestra los espectros preprocesados con segundas derivadas correspondientes a diferentes niveles de adulteración. — Figura\(\PageIndex{5}\): Preprocesamiento de espectros de carne de res para carne adulterada: (a) espectros crudos; (b) espectros preprocesados de SNV; (c) y (d) espectros preprocesados con derivados primero y segundo.

Los datos espectrales brutos (Figura 2.3.5a) tienen lo que probablemente sea ruido aleatorio con la señal, particularmente en las longitudes de onda más bajas (400—500 nm). La razón para decir esto es que hay variaciones en la magnitud espectral entre las muestras que no cambian linealmente con la concentración de adulteración. Es posible que estas variaciones (ruido en esta aplicación) se deban a diferencias en los componentes químicos de las muestras, ya que la carne en mal estado es muy diferente de la carne fresca, por lo que cuando las dos se mezclan en diferentes proporciones debería ser visible una señal clara. También se puede introducir ruido debido a pequeñas diferencias en la estructura física de las muestras que causan variación de la dispersión de la luz entre las muestras. También tenga en cuenta que solo hay picos limitados y hay un desplazamiento evidente en los espectros brutos. Por lo tanto, diferentes métodos de preprocesamiento, incluyendo el alisado S-G, SNV, y los derivados primero y segundo se pueden aplicar a los espectros crudos (Figura 2.3.5) y comparar su desempeño en términos de mejorar la detección de adulteración de carne de res.

El Cuadro 2.3.2 muestra el desempeño de diferentes métodos de preprocesamiento junto con PLSR en la determinación de la concentración de adulteración. Todos los métodos de preprocesamiento aplicados conducen a mejores modelos con RMSE más pequeños, aunque tal mejora no es mucho. El modelo óptimo se logró utilizando SNV como método de preprocesamiento, el cual tuvo coeficientes de determinación de 0.93, 0.92 y 0.88 así como RMSE de 7.30%, 8.35% y 7.90% para calibración, validación cruzada y predicción, respectivamente. Aunque los espectros de segunda derivada han contribuido a una mejor precisión de predicción (7.37%), el modelo correspondiente produjo RMSE más grandes tanto para calibración como para validación cruzada. Por lo tanto, el mejor método de preprocesamiento en este caso es SNV. Este método de preprocesamiento se puede incrustar en un espectrómetro de mano, donde los espectros crudos de muestras de carne adulterada adquiridas pueden normalizarse eliminando el promedio y luego dividiendo por la desviación estándar de los espectros. El modelo de predicción se puede aplicar a los datos preprocesados de SNV para estimar los niveles de adulteración de carne y proporcionar información sobre la autenticidad del producto de carne.

Cuadro\(\PageIndex{2}\): Comparación de diferentes métodos de preprocesamiento de datos combinados con PLSR para predecir la adulteración de carne de res.
Métodos	RMSEG (%)	RMSECV (%)	RMSEP (%)	R ² C	R ² CV	R ² P	LV
Ninguno	8.35	9.34	7.99	0.91	0.90	0.88	4
Derivada 1ª	8.05	8.78	7.92	0.92	0.91	0.88	3
2º Derivada	7.92	10.03	7.37	0.92	0.88	0.90	4
SNV	7.30	8.35	7.90	0.93	0.92	0.88	4
S-G	7.78	8.90	7.91	0.93	0.91	0.88	5
C = Calibración CV = coeficiente de variación SEP = error estándar de predicción P = predicción LV = variables latentes

Clasificación Bacteriana

La identificación y clasificación de bacterias son importantes para la inocuidad de los alimentos, para el diseño de procesos como el tratamiento térmico, y para ayudar a identificar las causas de la enfermedad cuando se ha producido contaminación bacteriana. Este ejemplo describe cómo se puede desarrollar un sistema de clasificación (Feng et al., 2015). Se obtuvo una matriz espectral escaneando un total de 196 suspensiones bacterianas de diversas concentraciones usando un espectrómetro de infrarrojo cercano en dos rangos de longitud de onda, es decir, 400—1100 nm y 1100—2498 nm. También se construyó un vector de columna que registraba los marcadores para cada bacteria (es decir, su nombre o clasificación). Este conjunto de datos se utilizó para clasificar diferentes bacterias, incluyendo tres cepas de Escherichia coli y cuatro cepas de Listeria innocua. Dado que el conjunto de datos contenía un gran número (>1000) de variables, fue interesante visualizar la estructura de los datos para investigar posibles agrupamientos de muestras. Mediante el uso de métodos de modelación apropiados, fue posible establecer un modelo para clasificar bacterias a nivel de especie.

PCA puede ser utilizado para entender la estructura de los datos. Dado que las puntuaciones de un modelo de PCA pueden utilizarse para dilucidar la distribución de muestras, es interesante dibujar una gráfica de puntuación como la Figura 2.3.6. Las dos primeras columnas de la matriz de puntuación T son las puntuaciones de las dos primeras PC y se genera utilizando la primera como eje x y la otra como eje y. Las gráficas de carga en la Figura 2.3.6 se pueden crear trazando las dos primeras columnas de la matriz de carga P ^T versus nombres de variables (longitudes de onda en este caso), respectivamente.

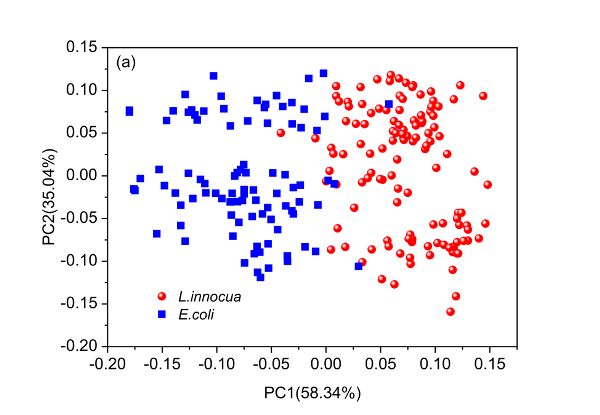
Gráfica de puntaje del modelo de análisis de componentes principales para suspensiones bacterianas de Escherichia coli y Listeria innocua.

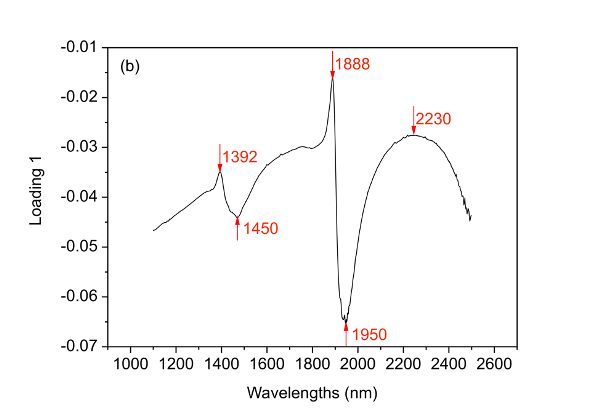
Cargando parcela uno de los modelos de análisis de componentes principales para suspensiones bacterianas Escherichia coli y Listeria innocua.

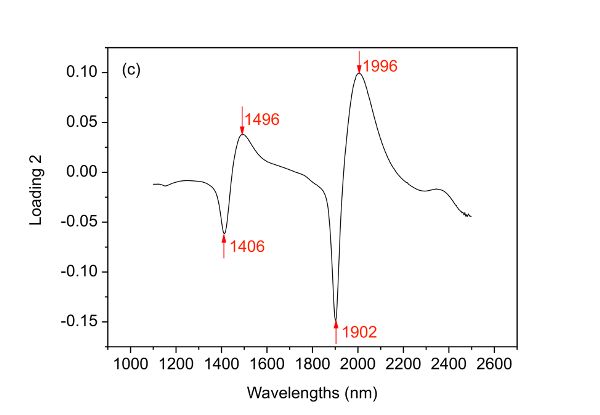
Cargando parcela dos del modelo de análisis de componentes principales para suspensiones bacterianas Escherichia coli y Listeria innocua. — Figura\(\PageIndex{6}\): Gráficas de puntuación y cargas del modelo PCA (1100—2498 nm) para suspensiones bacterianas de *E. coli* y *L. innocua*. (a) Gráfica de puntuación; (b) y (c) son cargas para las dos primeras PC (Feng et al., 2015).

El primer y segundo PC han cubierto 58.34% y 35.04% de la varianza total del conjunto de datos espectrales, lo que lleva a 93.38% de la información explicada. Con base en dicha información, se demuestra claramente que las dos bacterias están bien separadas a lo largo de la primera PC aunque muy pocas muestras se mezclan entre sí. Al investigar la carga 1, se encuentra que cinco longitudes de onda principales incluyendo 1392, 1450, 1888, 1950 y 2230 nm son variables importantes que contribuyen a la separación de las dos especies bacterianas. Además, es interesante encontrar que dos cúmulos aparecen dentro de cualquiera de las dos especies bacterianas y dicha separación puede explicarse entonces por las cuatro longitudes de onda principales indicadas en la carga 2 (Figura 2.3.6c).

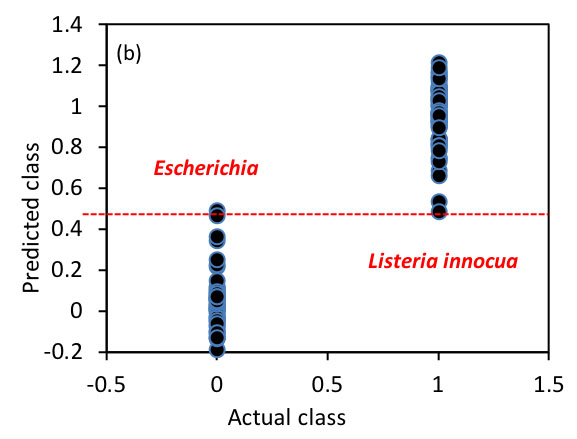
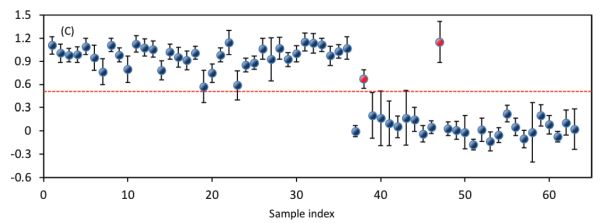
El siguiente objetivo es establecer un modelo de clasificación en la región de 400—1100 nm para la clasificación de estas especies bacterianas. Para lograr esto, se empleó PLS-DA donde se utilizan los datos espectrales y las etiquetas bacterianas como variables independientes y dependientes, respectivamente. La Figura 2.3.7 muestra el desempeño del modelo establecido. El modelo optimizado toma cuatro variables latentes para producir OCCR de 99.25% y 96.83% para calibración y predicción, respectivamente. Para calcular los OCCR, primero se redondean los valores predichos de muestras individuales para obtener valores de 1 o 0 y luego se comparan estas etiquetas predichas con las etiquetas verdaderas, después de lo cual se emplea la Ecuación 2.3.14.

En la Tabla 2.3.3 se muestra una matriz de confusión que muestra los detalles de clasificación para la predicción. Se muestra que los verdaderos positivos para detectar E. coli y L. innocua son 25 y 36, respectivamente. En consecuencia, la sensibilidad para detectar especies de E. coli y L. innocua son 0.93 (25/27) y 1 (36/36), respectivamente. Todos los parámetros anteriores tanto para la calibración como para la predicción demuestran que las dos especies bacterianas pueden clasificarse bien.

Cuadro\(\PageIndex{3}\): Matriz de confusión para la clasificación de especies bacterianas.
Clase Actual	Clase Predicha		Total
Clase Actual	E. coli	L. innocua	Total
E. coli	25	2	27
L. innocua	0	36	36
Total	25	38	63

En la inspección de seguridad microbiana de los productos alimenticios, es importante identificar a los patógenos culpables que son responsables de las enfermedades transmitidas por los alimentos. Para lograr esto, las bacterias en las superficies de los alimentos pueden ser muestreadas, cultivadas, aisladas y suspendidas, y el modelo se puede aplicar a los espectros de suspensiones bacterianas para decirnos cuáles de esas dos especies de bacterias están presentes en el producto alimenticio.

Un gráfico de líneas que muestra el número de variables latentes en el modelo de clasificación de análisis discriminante de mínimos cuadrados parciales.

Un gráfico de líneas que muestra el rendimiento del modelo para la predicción en el modelo de clasificación de análisis discriminante de mínimos cuadrados parciales. — Figura\(\PageIndex{7}\): Rendimiento del modelo de clasificación PLS-DA en el rango Visible-SWNIR (400—1100 nm). a) Selección del número óptimo de variables latentes; b) desempeño del modelo para calibración; c) desempeño del modelo para predicción. Las líneas punteadas indican el valor umbral de 0.5 (Feng et al., 2015).

Ejemplos

Ejemplo\(\PageIndex{1}\)

Ejemplo 1: Cálculo de la media móvil

Problema:

La variedad y madurez del fruto se pueden determinar por métodos no destructivos como la espectroscopia NIR. Se adquirió un espectro de reflectancia de una muestra de durazno; parte de los datos espectrales en el rango de longitud de onda de 640—690 nm se muestra en la Tabla 2.3.4. Aunque el espectrómetro está cuidadosamente configurado, aún puede haber ruido presente en los espectros debido a las condiciones ambientales. Aplicar el método de media móvil para suavizar el espectro y reducir el ruido potencial.

Solución

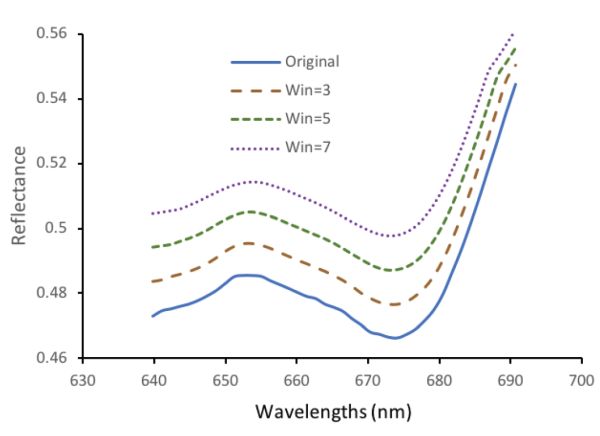
Varios programas, incluyendo Microsoft, MATLAB y software quimiométrico comercial (Unscrambler, PLS Toolbox etc.) están disponibles para implementar la media móvil. Tomando como ejemplo Microsoft Excel, se requiere la función “promedio”. Dado un espectro presentado por columna (por ejemplo, columna B), el valor para el espectro suavizado en la celda B10 se puede obtener como promedio (B9:B11) si el tamaño de ventana es 3, y promedio (B8:B12) o promedio (B7:B13) si el tamaño de ventana es 5 o 7, respectivamente. Para ambos extremos del espectro, solo se calcula el promedio de valores presentes en la ventana de un tamaño particular. Por ejemplo, el valor espectral a 639.8 nm después de suavizar la media móvil bajo el tamaño de ventana de 3 se puede obtener como los valores medios del espectro original a 639.8, 641.1 y 642.2 nm, es decir, (0.4728 + 0.4745 + 0.4751) /3 =0.4741.

La Figura 2.3.8 muestra el espectro suavizado, resultado de utilizar el método de la media móvil. Tenga en cuenta que los espectros se desplazan 0.01, 0.02 y 0.03 unidades para los espectros Win = 3, Win = 5 y Win = 7 para separar las curvas con fines de presentación visual. Es claro que para los datos originales, existe una ligera fluctuación y dicha variación disminuye después del suavizado de la media móvil.

Cuadro\(\PageIndex{4}\): Datos espectrales de una muestra de durazno en el rango 640—690 nm.
Longitud de onda (nm)	Reflectancia	Longitud de onda (nm)	Reflectancia
639.8	0.4728	665.2	0.4755
641.1	0.4745	666.5	0.4743
642.4	0.4751	667.7	0.4721
643.6	0.4758	669.0	0.4701
644.9	0.4766	670.3	0.4680
646.2	0.4777	671.5	0.4673
647.4	0.4791	672.8	0.4664
648.7	0.4807	674.1	0.4661
650.0	0.4829	675.3	0.4672
651.2	0.4850	676.6	0.4689
652.5	0.4854	677.9	0.4715
653.8	0.4854	679.2	0.4747
655.0	0.4851	680.4	0.4796
656.3	0.4838	681.7	0.4862
657.6	0.4826	683.0	0.4932
658.8	0.4814	684.3	0.5010
660.1	0.4801	685.5	0.5093
661.4	0.4789	686.8	0.5182
662.7	0.4782	688.1	0.5269
663.9	0.4765	689.3	0.5360

Ejemplo\(\PageIndex{2}\)

Ejemplo 2: Evaluación del desempeño del modelo

Problema:

Como los cerdos no pueden sudar, es importante poder confirmar rápidamente que las condiciones en una casa de cerdos no les están causando estrés. La temperatura rectal es el mejor indicador de estrés por calor en un animal, pero puede ser difícil de medir. Sin embargo, la temperatura de la superficie de un cerdo se puede medir fácilmente usando sensores sin contacto. En el Cuadro 2.3.5 se muestra el desempeño de dos modelos de PLSR utilizados para predecir la temperatura rectal de los cerdos mediante el uso de variables que incluyen la temperatura superficial y varias condiciones ambientales. El modelo 1 es un modelo de muchas variables y el modelo 2 es un modelo simplificado que utiliza un subconjunto optimizado de variables. Determinar qué modelo es mejor. El desempeño de los modelos es presentado por R y RMSE para calibración, validación cruzada y predicción.

Solución

El primer paso es verificar si R está cerca de 1 y RMSE a 0. Los coeficientes de correlación oscilan entre 0.66 y 0.87 (Cuadro 2.3.5), mostrando una correlación obvia entre la temperatura rectal predicha y la temperatura rectal real. Al investigar los RMSE, se encuentra que estos errores son relativamente pequeños (0.25°—0.38°C) en comparación con el rango medido (37.8°—40.2°C). Por lo tanto, ambos modelos son útiles para predecir la temperatura rectal de los cerdos.

Un gráfico de líneas que traza el suavizado de promedio móvil de un espectro de durazno. Se muestran el espectro original y los espectros con anchos de ventana de tres, cinco y siete. — Figura\(\PageIndex{8}\): Ejemplo de suavizado de media móvil de un espectro de durazno. Los espectros se desplazan 0.01, 0.02 y 0.03 unidades para Win = 3, Win = 5 y Win = 7 espectros, respectivamente, para una mejor presentación visual.

El segundo paso es verificar la estabilidad de los modelos establecidos evaluando la diferencia entre Rs o RMSE para calibración, validación cruzada y predicción. Para el ejemplo específico, aunque se obtuvieron el mejor coeficiente de correlación para calibración (_RC) y error cuadrático medio para calibración (RMSEC) para el modelo de muchas variables, su desempeño en validación cruzada y predicción fue inferior al del modelo simplificado. Lo más importante es que la mayor diferencia entre las Rs del modelo de muchas variables fue de 0.21, mientras que solo se encontró una décima parte de dicha diferencia (0.02) para el modelo simplificado. También se observó una tendencia similar para las RMSE donde se obtuvieron las diferencias máximas de 0.05°C y 1.3°C para los modelos simplificados y de muchas variables, respectivamente. Estos resultados demuestran fuertemente que el modelo simplificado es mucho más estable que el modelo de muchas variables.

Cuadro\(\PageIndex{5}\): Comparación del desempeño de dos modelos, el Modelo 1 de muchas variables y el Modelo 2 simplificado (Feng et al., 2019). RC, RCV y RP son coeficientes de correlación para calibración, validación cruzada y predicción, respectivamente.
Modelo	RC	RCV	RP	RMSEC (°C)	RMSECV (°C)	RMSEP (°C)	LV
Modelo 1	0.87	0.66	0.76	0.25	0.38	0.37	4
Modelo 2	0.80	0.78	0.80	0.30	0.32	0.35	2

El tercer paso puede evaluar la simplicidad del modelo. En este ejemplo, se emplearon cuatro variables latentes para establecer el modelo de muchas variables mientras que solo se necesitaron dos para el modelo simplificado. Sobre todo, el modelo simplificado mostró mejor capacidad de predicción, particularmente para validación cruzada y predicción, con menos variables latentes. Por lo tanto, se considera como el mejor modelo.

Créditos de imagen

Figura 1. Feng, Y. (CC Por 4.0). (2020). Alisado S-G de una señal espectral.

Figura 2. Feng, Y. (CC Por 4.0). (2020). Espectros derivados NIR de suspensiones bacterianas.

Figura 3. Feng, Y. (CC Por 4.0). (2020). Procesamiento SNV de espectros Vis-NIR de muestras de carne adulterada con carne de pollo.

Figura 4. Feng, Y. (CC Por 4.0). (2020). Gráfica del error cuadrático medio (RMSE) como función del número de variables latentes (LV) para un modelo PLSR.

Figura 5. Feng, Y. (CC Por 4.0). (2020). Preprocesamiento de espectros de carne.

Figura 7. Feng, Y. (CC Por 4.0). (2020). Rendimiento del modelo de clasificación PLS-DA en el rango Visible-SWNIR (400—1000 nm).

Figura 8. Feng, Y. (CC Por 4.0). (2020). Ejemplo de suavizado de media móvil de un espectro de durazno.

Agradecimiento

Muchas gracias al señor Hai Tao Zhao por su ayuda en la preparación de este capítulo.

Referencias

Bai, X., Wang, Z., Zou, L., & Alsaadi, F. E. (2018). Estimación colaborativa de fusión a través de redes de sensores inalámbricos para monitorear la concentración de CO ₂ en un invernadero. Fusión de información, 42, 119-126. https://doi.org/10.1016/j.inffus.2017.11.001.

Baietto, M., & Wilson, A. D. (2015). Aplicaciones de nariz electrónica para identificación de frutos, madurez y clasificación de calidad. Sensores, 15 (1), 899-931. https://doi.org/10.3390/s150100899.

Dhanoa, M. S., Lister, S. J., Sanderson, R., & Barnes, R. J. (1994). El vínculo entre la corrección de dispersión multiplicativa (MSC) y las transformaciones estándar de variación normal (SNV) de espectros NIR. J. Espectroscopia de infrarrojo cercano, 2 (1), 43-47. https://doi.org/10.1255/jnirs.30.

Feng, Y.-Z., & Dom, D.-W. (2013). Imágenes hiperespectrales del infrarrojo cercano en tándem con regresión de mínimos cuadrados parciales y algoritmo genético para la determinación no destructiva y visualización de cargas de Pseudomonas en filetes de pollo. Talanta, 109, 74-83. https://doi.org/10.1016/j.talanta.2013.01.057.

Feng, Y.-Z., Downey, G., Dom, D.-W., Walsh, D., & Xu, J.-L. (2015). Hacia la mejora en la clasificación de Escherichia coli, Listeria innocua y sus cepas en sistemas aislados basados en el análisis quimiométrico de datos espectroscópicos visibles e infrarrojos cercanos. J. Food Ing. , 149, 87-96. https://doi.org/10.1016/j.jfoodeng.2014.09.016.

Feng, Y.-Z., ElmaSry, G., Dom, D.-W., Scannell, A. G., Walsh, D., & Morcy, N. (2013). Imágenes hiperespectrales del infrarrojo cercano y regresión de mínimos cuadrados parciales para la determinación rápida y sin reactivos de Enterobacteriaceae en filetes de pollo. Alimentos Chem. , 138 (2), 1829-1836. https://doi.org/10.1016/j.foodchem.2012.11.040.

Feng, Y.-Z., Zhao, H.-T., Jia, G.-F., Ojukwu, C., & Tan, H.-Q. (2019). Establecimiento de modelos validados para la predicción no invasiva de la temperatura rectal de cerdas mediante termografía infrarroja y quimiometría. Int. J. Biometeorol. , 63 (10), 1405-1415. https://doi.org/10.1007/s00484-019-01758-2.

Friedman, J., Hastie, T., & Tibshirani, R. (2001). Los elementos del aprendizaje estadístico. No. 10. Nueva York, NY: Springer.

Ganesh, S. (2010). Regresión lineal multivariada. En P. Peterson, E. Baker, & B. McGaw (Eds.), Enciclopedia internacional de la educación (pp. 324-331). Oxford: Elsevier. https://doi.org/10.1016/B978-0-08-044894-7.01350-6.

Gauch, H. G., Hwang, J. T., & Fick, G. W. (2003). Evaluación del modelo mediante comparación de predicciones basadas en modelos y valores medidos. Agron. J., 95 (6), 1442-1446. doi.org/10.2134/agronj2003.1442.

Geladi, P., & Kowalski, B. R. (1986). Regresión parcial por mínimos cuadrados: Un tutorial. Anal. Chim. Acta, 185, 1-17. https://doi.org/10.1016/0003-2670(86)80028-9.

Gowen, A. A., O'Donnell, C. P., Cullen, P. J., Downey, G., & Frias, J. M. (2007). Imágenes hiperespectrales: una herramienta emergente de análisis de procesos para el control de la calidad e inocuidad de Tendencias Alimentación Sci. Tecnol. , 18 (12), 590-598. doi.org/10.1016/j.jpgs.2007.06.001.

Hotelling, H. (1933). Análisis de un complejo de variables estadísticas en componentes principales. J. Ed. Psicólico. , 24, 417-441. https://doi.org/10.1037/h0071325.

Klanke, S., & Ritter, H. (2006). Un esquema de validación cruzada de ausencia-k-out para regresión de kernel no supervisada. En S. Kollias, A. Stafylopatis, W. Duch, & E. Oja (Eds.), Proc. Int. Conf. Redes Neuronales Artificiales. 4132, pp. 427-436. Springer. doi: doi.org/10.1007/11840930_44.

LeCun, Y., Bengio, Y., & Hinton, G. (2015). Aprendizaje profundo. Naturaleza, 521 (7553), 436-444. doi.org/10.1038/naturaleza14539.

Maione, C., & Barbosa, R. M. (2019). Aplicaciones recientes de los métodos de análisis de datos multivariados en la autenticación del arroz y los parámetros más analizados: Una revisión. Critical Rev. Alimentación Sci. Nutrición, 59 (12), 1868-1879. https://doi.org/10.1080/10408398.2018.1431763.

Mevik, B.-H., Wehrens, R., & Liland, K. H. (2011). PLS: Mínimos cuadrados parciales y regresión de componentes principales. Paquete R ver. 2 (3). Recuperado de https://cran.r-project.org/web/packages/pls/pls.pdf.

O'Donnell, C. P., Fagan, C., & Cullen, P. J. (2014). Tecnología analítica de procesos para la industria alimentaria. Nueva York, NY: Springer. doi.org/10.1007/978-1-4939-0311-5.

Park, B., & Lu, R. (2015). Tecnología de imágenes hiperespectrales en alimentación y agricultura. Nueva York, NY: Springer. doi.org/10.1007/978-1-4939-2836-1.

Pham, B. T., Jaafari, A., Prakash, I., & Bui, D. T. (2019). Un novedoso modelo inteligente híbrido de máquinas vectoriales de soporte y el conjunto MultiBoost para el modelado de susceptibilidad a deslizamientos de tierra. Toro. Ing. Geol. El medio ambiente. , 78 (4), 2865-2886. doi.org/10.1007/s10064-018-1281-y.

Savitzky, A., & Golay, M. J. (1964). Suavización y diferenciación de datos mediante procedimientos simplificados de mínimos cuadrados. Anal. Chem. , 36 (8), 1627-1639. doi.org/10.1021/ac60214a047.

Townsend, J. T. (1971). Análisis teórico de una matriz de confusión alfabética. Percepción Psicofísica, 9 (1), 40-50. doi.org/10.3758/BF03213026.

Zhao, H.-T., Feng, Y.-Z., Chen, W., & Jia, G.-F. (2019). Aplicación de optimización invasiva de malezas y máquina vectorial de soporte mínimo cuadrado para la predicción de adulteración de carne de res con carne en mal estado basada en imágenes hiperespectrales visibles del infrarrojo cercano (vis-NIR). Carne Sci. , 151, 75-81. https://doi.org/10.1016/j.meatsci.2019.01.010.

Variables