3.1: Tracción
- Page ID
- 80906
Daniel M. Queiroz
Departamento de Ingeniería Agropecuaria
Universidad Federal de Vicosa
Viçosa, Minas Gerais, Brasil
John Schueller
Departamento de Ingeniería Mecánica y Aeroespacial
Universidad de Florida
Gainesville, Florida, Estados Unidos
| Términos Clave |
| Mecánica de tracción | Dispositivos de tracción | Tractores |
| Potencia del motor | Dispositivos de transporte | Implementos tirados |
| Fuerza de tracción |
Variables
Introducción
Se crearon tractores para reducir los insumos de mano de obra humana y animal y aumentar la eficiencia y productividad en las actividades de producción de cultivos (Schueller, 2000). El uso principal de los tractores es tirar de implementos como herramientas de labranza, sembradoras, cultivadoras y cosechadoras en el campo y, en cierta medida, en la carretera (Renius, 2020). Para tirar de los implementos de manera eficiente, un tractor necesita generar tracción entre las llantas y la superficie del suelo. La tracción es la forma en que un vehículo usa la fuerza para moverse sobre una superficie.
Muy temprano en el desarrollo del tractor, la transferencia directa de energía de los tractores a los implementos fue posible mediante el uso de tomas de fuerza (PTO) que transfieren energía rotativa a implementos y máquinas y mediante el uso de sistemas hidráulicos para levantar y bajar implementos y para mover partes de máquinas conectadas. Tirar implementos sigue siendo el uso más común de la potencia del tractor. La capacidad de campo de las máquinas agrícolas, es decir, el área de campo que puede cubrirse por unidad de tiempo, ha provocado que se desarrollen y utilicen implementos más grandes. Los mayores tamaños requieren una mayor tracción del tractor de tracción. Se necesitan sistemas más eficientes para crear la fuerza de tracción para proporcionar las grandes fuerzas necesarias para tirar de esos implementos.
La eficiencia de cómo los tractores convierten la potencia generada por un motor a la potencia requerida para tirar de los implementos depende de muchas variables asociadas con el tractor y las condiciones del suelo. La tracción es especialmente importante en la agricultura ya que los suelos de campo no son tan firmes como las carreteras utilizadas por los automóviles y camiones. En este capítulo se presentan los principios básicos de tracción aplicados a la maquinaria agrícola.
Resultados
Después de leer este capítulo, deberías poder:
- • Explicar cómo los tractores desarrollan fuerza de tracción
- • Describir el efecto de algunas variables importantes sobre la fuerza de tracción
- • Calcular cuánta potencia puede desarrollar un tractor al tirar de un implemento
- • Calcular los requisitos de potencia para hacer coincidir tractores con implementos
Conceptos
Dispositivos de Tracción y Transporte
Según la Sociedad Americana de Ingenieros Agrícolas y Biológicos (ASABE Standards, 2018), existen dos tipos de dispositivos de contacto superficial asociados al movimiento de un vehículo: los dispositivos de tracción y los dispositivos de transporte. Un dispositivo de tracción recibe potencia de un motor y utiliza las reacciones de las fuerzas de la superficie de soporte para impulsar el vehículo, mientras que un dispositivo de transporte no recibe energía, sino que es necesario para soportar el vehículo en una superficie mientras el vehículo se mueve sobre esa superficie. Las ruedas, llantas y orugas pueden ser dispositivos de tracción si están conectados a un motor u otra fuente de energía; si no están conectados, son dispositivos de transporte. Los componentes principales de un tractor agrícola se presentan en la Figura 3.1.1. En este ejemplo, el tractor tiene tracción a las 2 ruedas, por lo que las ruedas traseras grandes, que reciben potencia del motor, son los dispositivos de tracción, y las ruedas delanteras pequeñas son los dispositivos de transporte. Todas las ruedas serían dispositivos de tracción si el tractor tuviera tracción a las 4 ruedas. El motor está conectado al dispositivo de tracción por el tren de transmisión, que a menudo consiste en un embrague, transmisión, diferencial, ejes y otros componentes. (El tren motriz no se discute en este capítulo.) La barra de tiro es un punto de fijación a través del cual el tractor puede aplicar fuerza de tracción a un implemento.
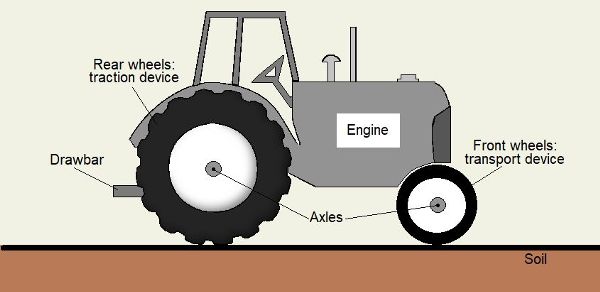
Mecánica de Tracción
La forma más sencilla de analizar la tracción producida por un dispositivo de tracción, como una rueda o una pista, es considerar las fuerzas de fricción que actúan en el contacto entre un dispositivo de tracción y la superficie cuando el sistema está en equilibrio. Para simplificar se supone que la máquina se mueve a velocidad constante sobre una superficie no variable (Figura 3.1.2). Un dispositivo de tracción (en adelante simplificado a la implementación más común como “rueda”) tiene dos funciones principales: soportar la carga que actúa sobre el eje de la rueda (W) y producir una fuerza de tracción neta (H). La fuerza W se denomina generalmente la carga dinámica que actúa sobre la rueda. La carga dinámica depende de cómo se distribuya el peso del tractor en ese momento a cada rueda. Si el sistema está en equilibrio, la superficie reacciona a W aplicando una fuerza de reacción vertical (R) a la rueda. En el contacto entre la superficie y la rueda, se genera una fuerza de fricción (F f). Para mantener el equilibrio en la dirección horizontal, la magnitud de la fuerza de tracción neta H es igual a la magnitud de la fuerza de fricción F f. Para producir una fuerza de tracción neta H, es necesario superar la fuerza de fricción. Esto se hace aplicando un par (T) al eje de la rueda. Este par es proporcional al par producido por el motor del tractor de acuerdo con el tren de transmisión, incluyendo la relación de transmisión actual.
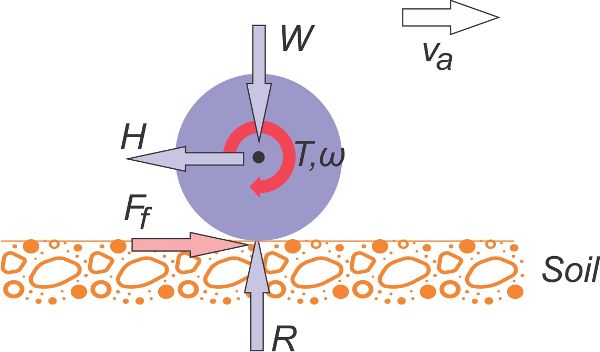
Al moverse, la rueda (Figura 3.1.2) gira con una velocidad angular constante (ω), y esta velocidad angular es proporcional a la velocidad de rotación del motor, dependiendo de la relación de transmisión en el tren de transmisión. La rueda tiene una velocidad real v a, que es igual a la velocidad angular multiplicada por el radio de rodadura de la rueda reducido por el deslizamiento (como se analiza a continuación). En una situación de equilibrio, ω y v a son constantes. La potencia transferida al eje de rueda (Pw) se puede calcular como el producto del par (T) y la velocidad angular (ω), como se muestra en la Ecuación 3.1.1. La potencia de tracción desarrollada por la rueda (P t) es el producto de la fuerza de tracción neta (H) y la velocidad real (v a), como se muestra en la Ecuación 3.1.2. La eficiencia de tracción de la rueda (T E) se puede calcular como la relación entre la potencia de tracción y la potencia del eje de la rueda, como se muestra en la Ecuación 3.1.3.
\[ P_{W}=T\omega \]
\[ P_{t}=H\nu_{a} \]
\[ T_{E}=\frac{P_{t}}{P_{W}} \]
donde P w = potencia transferida al eje de la rueda (W)
T = par transferido al eje de la rueda (N m)
ω = velocidad angular de la rueda (rad s −1)
P t = potencia de tracción desarrollada por la rueda (W)
H = fuerza de tracción neta (N)
v a = velocidad real de la rueda (m s −1)
T E = eficiencia de tracción de la rueda (adimensional)
La fuerza de fricción (F f en la Figura 3.1.2) es generada por la interacción entre la rueda y la superficie. La fuerza de fricción se puede calcular multiplicando la fuerza de reacción (R) por el coeficiente de fricción equivalente (μ). El Cuadro 3.1.1 presenta algunos valores típicos. Debido a que R es igual a la carga dinámica que actúa sobre el eje de la rueda (W) y la fuerza de tracción neta es igual a la fuerza de fricción, la fuerza de tracción se puede calcular como el producto del coeficiente de fricción equivalente y la carga dinámica, como:
| Tipo de superficie | Coeficiente equivalente de fricción (μ) [a] |
|---|---|
|
Suelo blando |
0.26—0.31 |
|
Suelo medio |
0.40—0.46 |
|
Suelo firme |
0.43—0.53 |
|
Concreto |
0.91—0.98 |
[a] Estos valores se estimaron con base en datos presentados por Kolator y Bialobrzewski (2011).
\[ H= \mu W \]
donde μ = coeficiente de fricción (adimensional).
La velocidad teórica (v t) está determinada por la velocidad de rotación de la rueda (ω) multiplicada por el radio de rodadura (r) como se muestra en la Ecuación 3.1.5, pero la velocidad real de la rueda (v a) es menor debido al movimiento relativo en la interfaz entre la rueda y la superficie. Este movimiento relativo es la relación de reducción de desplazamiento, comúnmente llamada deslizamiento, y se define como la relación entre la pérdida de velocidad de la rueda y la velocidad teórica, es decir, la velocidad que tendría la rueda si no hubiera pérdida. La ecuación 3.1.6 muestra cómo se puede estimar la relación de reducción de desplazamiento:
\[ \nu_{t} = \omega r \]
\[ s= \frac{\nu_{t}-\nu_{a}}{\nu_{t}} \]
donde v t = velocidad teórica de la rueda (m s −1)
r = radio de rodadura de la rueda (m s −1)
s = relación de reducción de desplazamiento, o deslizamiento (adimensional)
La relación de reducción de desplazamiento es una variable importante para el análisis de la fuerza de tracción de la rueda. La relación de reducción de desplazamiento de una rueda puede variar de 0 a 1 dependiendo de las condiciones de rueda y superficie. Cuando la relación de reducción de desplazamiento es igual a 0, no habría movimiento relativo entre la periferia de la rueda y la superficie. La rotación de la rueda provoca un movimiento de traslación perfecto en relación con la superficie. Sin embargo, la experiencia ha demostrado que para que una rueda desarrolle una fuerza de tracción, debe haber un movimiento relativo (deslizamiento) entre la rueda y la superficie. Por lo tanto, una rueda que genera fuerza de tracción necesita tener una relación de reducción de desplazamiento mayor a cero. Cuando una rueda genera más fuerza de tracción, la relación de reducción de desplazamiento aumenta y la velocidad real de la rueda se reduce. Cuando la relación de reducción de desplazamiento es igual a 1, la rueda no se mueve hacia adelante cuando gira. Los modelos utilizados para calcular la fuerza de tracción generalmente utilizan la relación de reducción de desplazamiento como una de las variables.
Otro concepto importante al analizar el proceso de tracción de una rueda móvil es la fuerza de resistencia al movimiento (F r) (Figura 3.1.3). Si una rueda se mueve, la rueda y la superficie se deforman. La energía se gasta para producir esta deformación. La resistencia producida por la rueda y las deformaciones superficiales deben ser superadas para permitir que la rueda se mueva. Considerando la existencia de la fuerza de resistencia al movimiento, en el contacto entre la rueda y la superficie, es necesario generar una fuerza de fricción mayor que la fuerza de resistencia al movimiento en el contacto rueda-superficie para producir una fuerza de tracción. Esta fuerza de fricción ahora se denomina fuerza de tracción bruta (denotada por F). Así, la fuerza de tracción bruta sería la fuerza de tracción neta generada por la rueda si no hubiera resistencia al movimiento. Al sumar los conceptos de resistencia al movimiento y fuerzas de tracción brutas a la Figura 3.1.2 se obtiene como resultado la Figura 3.1.3, que es una representación mejorada de las fuerzas que actúan sobre una rueda.
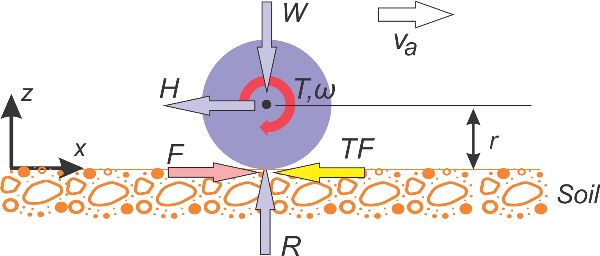
Si la rueda representada en la Figura 3.1.3 no tiene movimiento en la dirección vertical (eje z), la rueda está en equilibrio estático en esta dirección. En esta condición, la suma de fuerzas en la dirección z (vertical) es cero. Por lo tanto,
\[ \sum F_{z} = 0 \]
\[ R-W=0 \]
\[ R=W \]
donde F z = cualquier fuerza aplicada a la rueda en la dirección z (N)
R = fuerza de reacción vertical de la rueda (N)
Si la velocidad real de la rueda representada en la Figura 3.1.3 es constante, las fuerzas horizontales están en equilibrio estático en esta dirección y la suma de las fuerzas horizontales es cero. Por lo tanto,
\[ \sum F_{x}=0 \]
donde F x = cualquier fuerza aplicada a la rueda en la dirección x (N)
F = fuerza de tracción bruta (N)
F r = fuerza de resistencia al movimiento (N)
Con base en la Ecuación 3.1.12, la fuerza de tracción bruta (F) debe ser la fuerza de tracción neta (H) más la fuerza de resistencia al movimiento (F r). Si ambos lados de la Ecuación 3.1.12 se dividen por la carga dinámica (W) que actúa sobre la rueda, dando como resultado la Ecuación 3.1.13, se crean tres números adimensionales, es decir, μ n, μ g y ρ, como se muestra en las Ecuaciones 3.1.15, 3.1.16 y 3.1. 17. La primera es la relación de tracción neta (μ n), definida como la fuerza de tracción neta dividida por la carga dinámica. La segunda es la relación bruta de tracción (μ g), definida como la fuerza de tracción bruta dividida por la carga dinámica. Y la tercera es la relación de resistencia al movimiento (μ), definida como la fuerza de resistencia al movimiento dividida por la carga dinámica.
\[ \frac{H}{W}=\frac{F}{W}-\frac{F_{r}}{W} \]
La ecuación 3.1.14 muestra que μ n, μ g y ρ no son independientes. Mediante el uso de una técnica llamada análisis dimensional, se desarrollaron funciones para predecir cómo cambian μ g y ρ en función de las variables de rueda y la resistencia del suelo. Este análisis es presentado por Goering et al. (2003) y está más allá del alcance de este capítulo. Si se conocen μ g, ρ y W, la fuerza de tracción generada por la rueda se puede predecir usando la Ecuación 3.1.18:
\[ H= (\mu_{g}-\rho)W \]
Las fuerzas R, F y F r (Figura 3.1.3) actúan sobre un punto llamado centro de resistencia de rueda. Este punto no está alineado con la dirección de la carga dinámica W sino que está un poco por delante de ella. Esta distancia horizontal se denomina desplazamiento horizontal (e). El análisis estático de una rueda remolcada (Figura 3.1.4) muestra que el centro de resistencia de la rueda no está alineado con la dirección de la carga dinámica de la rueda. En una rueda remolcada, no hay par aplicado a su eje. La reacción del suelo (G) en el centro de resistencia es la resultante de las fuerzas R y F r. La dirección de la fuerza G pasa a través del centro de la rueda. Para mover la rueda remolcada a una velocidad real constante (v a), se necesita aplicar a la rueda una fuerza de tracción neta (H) igual a la fuerza de resistencia al movimiento (F r). Para que la rueda mantenga constante una velocidad angular, la suma de los momentos en el centro de las ruedas debe ser igual a cero. Goering et al. (2003) mostraron que el desplazamiento horizontal se puede calcular con las Ecuaciones 3.1.19-3.1.21.
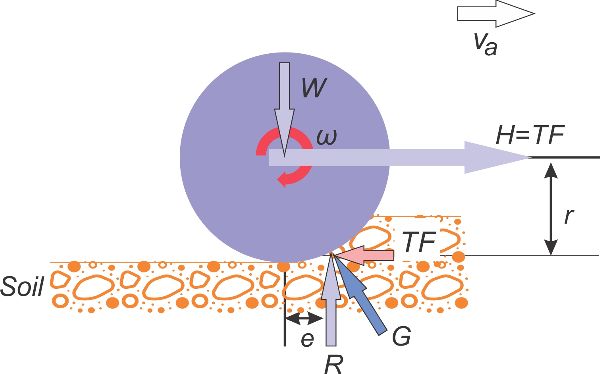
\[ Re-F_{r}r = 0 \]
donde e = desplazamiento horizontal (m).
Mediante el uso de la Ecuación 3.1.18, se puede predecir la fuerza de tracción. La otra información importante en el análisis de tracción de las ruedas es predecir cuánto par necesita transferirse al eje de la rueda para generar la fuerza de tracción (H). En la Ecuación 3.1.5, el radio de rueda se utiliza para convertir la velocidad angular de rotación a la velocidad teórica de la rueda. El radio de la rueda también se puede utilizar para calcular el par necesario para producir la fuerza de tracción de la rueda. El par (T) necesario para mantener constante la velocidad angular de la rueda y producir la fuerza de tracción neta es el producto de la fuerza de tracción bruta y el radio de par de torsión de la rueda, dado por:
donde r t = radio de par de la rueda (m).
El radio de rueda definido en la Ecuación 3.1.5 es diferente del radio de torsión de la rueda definido en la Ecuación 3.1.22 debido a la interacción de la rueda y la superficie, que varía en una superficie de suelo blando. Generalmente, se utiliza un radio de rodadura basado en la distancia desde el centro del eje de la rueda hasta una superficie dura. Por lo tanto, la Ecuación 3.1.23 se puede utilizar para estimar el par que actúa en el eje de la rueda:
\[ T=Fr \]
Potencia del motor necesaria para producir una fuerza de tracción
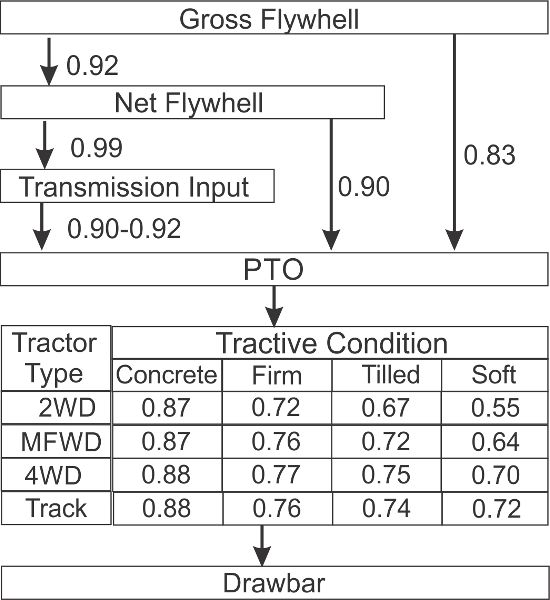
ASABE Standards (2015) presentó un diagrama (Figura 3.1.5) de la relación de potencia típica aproximada para tractores agrícolas. Los tractores pueden especificarse por su potencia nominal bruta del volante del motor (P e). Uno de los estándares utilizados para definir la potencia nominal bruta del volante del motor es SAE J1995 (SAE, 1995). La potencia nominal definida por esta norma es la potencia mecánica producida por el motor sin algunos de sus accesorios (como el alternador, el ventilador del radiador y la bomba de agua). Por lo tanto, la potencia nominal bruta del volante del motor es mayor que la potencia neta producida por el motor. La potencia neta aproximada del volante del motor se puede estimar multiplicando la potencia bruta del volante por 0.92. La potencia en la PTO del tractor es aproximadamente igual a la potencia bruta del volante del motor multiplicada por 0.83 o la potencia neta del volante del motor multiplicada por 0.90.
La potencia que el tractor puede generar para tirar de los implementos, a menudo denominada potencia de la barra de tiro porque muchos implementos están unidos a la barra de tracción del tractor, depende del tipo de tractor, es decir, tracción a las 2 ruedas (2WD), tracción delantera mecánica (MFWD), tracción a las 4 ruedas (4WD) o orugas. La condición de la superficie donde se utiliza el tractor tiene un efecto aún mayor. Usando estas dos piezas de información, los coeficientes que muestran estimaciones de la relación entre la potencia de la barra de tracción y la potencia de PTO se dan en la Figura 3.1.5.
La potencia de la barra de tracción requerida para tirar de un implemento es:
\[ P_{DB} = F_{i} \nu_{i} \]
donde P DB = potencia de la barra de tiro (W)
F i = fuerza requerida para tirar de un implemento (N)
v i = velocidad del implemento (m s −1)
La fuerza requerida para tirar de un implemento depende del implemento. Por ejemplo, la fuerza requerida para tirar de una sembradora F p es la fuerza requerida por fila multiplicada por el número de filas:
\[ F_{p} = f_{r}n_{r} \]
donde f r = fuerza requerida por hilera de sembradora (N fila −1)
n r = número de filas
Una vez que se determina la potencia requerida de la barra de tracción, los valores de la Figura 3.1.5 se pueden utilizar para calcular la potencia nominal bruta necesaria estimada del volante de un tractor para tirar del implemento.
Aplicaciones
Los conceptos de tracción y potencia del tractor son necesarios para adecuar correctamente el tractor a un implemento. Las operaciones agrícolas no se pueden realizar si el tractor no puede desarrollar suficiente potencia o tracción para tirar del implemento. Como los implementos han aumentado de tamaño a lo largo de los años, es necesario que los tractores tengan suficiente potencia y suficiente tracción para las tareas que tienen que realizar. Elegir un tractor que sea demasiado grande tendrá un impacto negativo en la rentabilidad agrícola porque los tractores más grandes cuestan más que los tractores más pequeños. Un tractor de gran tamaño también puede aumentar el consumo de combustible y las emisiones de escape. Esto es significativo porque incluso los tractores más eficientes obtienen menos de 4 kWh de trabajo por litro de combustible diesel.
Los tractores varían mucho en tamaño (por ejemplo, Figura 3.1.6). Por ejemplo, un gran fabricante contemporáneo vende tractores de 17 a 477 kW. El peso del tractor debe ser suficiente para generar suficiente fuerza de tracción, como se muestra en la Ecuación 3.1.18. Sin embargo, además del costo de agregar peso, el peso adicional puede aumentar la compactación del suelo y deprimir los rendimientos de los cultivos. Por lo tanto, es necesario comprender estos conceptos para diseñar tractores e implementos. Las capacidades del motor del tractor, los elementos de transmisión de potencia y las ruedas deben escalarse adecuadamente. Debe haber una compensación entre hacerlos grandes y poderosos y hacerlos compactos y económicos. Los análisis anteriores se pueden utilizar para guiar la elección y el diseño del tractor.


Los conceptos también se aplican a otros tipos de maquinaria agrícola, como cosechadoras autopropulsadas y pulverizadores. Para que estas máquinas puedan completar sus tareas, necesitan poder moverse a través de suelos agrícolas. Los mismos cálculos se pueden utilizar para determinar si hay suficiente potencia y para diseñar los diversos componentes en esas máquinas. Las ruedas, los ejes y los componentes de la transmisión de potencia deben ser capaces de soportar las fuerzas, los pares y la potencia durante el uso de las máquinas.
Ejemplos
Ejemplo\(\PageIndex{1}\)
Ejemplo 1: Fuerza de tracción
Problema:
Calcular la fuerza de tracción producida por una rueda tractora que trabaja en un suelo firme con una carga dinámica de 5 kN. La velocidad de la rueda es de 2 m s −1. Si la eficiencia de tracción es 0.73, ¿cuál es la potencia que se necesita transferir al eje de la rueda?
Solución
Asumir un coeficiente de fricción equivalente de 0.48, el valor medio para suelo firme presentado en el Cuadro 3.1.1. Calcular la fuerza de tracción usando la Ecuación 3.1.4:
\( H= \mu W=0.48 \times 5 = 2.4 \text{ kN} \)
Ahora, calcule la potencia de tracción para la rueda del tractor usando la Ecuación 3.1.2:
\( P_{t} = H\nu_{a} = 2.4 \times 2 = 4.8 \text{ kW} \)
Calcule la potencia que necesita transferirse al eje de la rueda para usar la Ecuación 3.1.3 con la eficiencia de tracción dada de 0.73:
\( P_{W} = \frac{P_{t}}{T_{E}} = \frac{4.8}{0.73} = 6.58 \text{ kW} \)
Este valor de potencia necesaria se puede utilizar para diseñar los diversos componentes de transmisión de potencia. El consumo de energía también se puede utilizar para calcular la potencia demandada de la fuente de energía definitiva, probablemente un motor, para calcular el consumo de combustible y, con ello, los costos de una operación de campo particular.
Ejemplo\(\PageIndex{2}\)
Ejemplo 2: Relación de reducción de par y desplazamiento, o deslizamiento
Problema:
Una rueda en otro tractor recibe 40 kW del tren motriz del tractor. La rueda gira a 25 rpm, que es una velocidad angular, ω, de 2.62 rad s −1. (Nota: 2π rad × 25 rpm/60 min s −1 = 2.62 rad s −1.) Si el radio de rodadura de las ruedas es de 0.81 m y la velocidad del tractor es de 2 m s −1, calcule el par que actúa sobre la rueda y la relación de reducción de desplazamiento (comúnmente conocida como deslizamiento).
Solución
Calcule el par que actúa sobre la rueda T para una potencia P w de 40 kW usando la Ecuación 3.1.1:
\( T=\frac{P_{W}}{\omega} = \frac{40}{2.62} = 15.28 \text{ Nm} \)
Calcule la potencia a transferir a la rueda para producir 2.4 kN de fuerza de tracción a 2 m s −1 de velocidad de rueda usando la Ecuación 3.1.3:
\( P_{W} = \frac{P_{t}}{T_{E}} = \frac{4.8}{0.73} =6.58 \text{ kW} \)
Calcular la velocidad teórica de la rueda v t para un radio de rodadura r de 0.81 m usando la Ecuación 3.1.5:
\( \nu_{t} = \omega r = 2.62 \times 0.81 = 2.12 \text{ m}s^{-1} \)
Dado que la velocidad real de la rueda es de 2 m s −1, que es menor que la velocidad teórica de la rueda, calcule la relación de reducción de desplazamiento s usando la Ecuación 3.1.6:
\( s= \frac{\nu_{t}-\nu_{a}}{\nu_{t}} = \frac{2.12-2.00}{2.12} = 0.057, \text{or} \ 5.7\% \)
Además de brindar orientación al diseño de la máquina agrícola y su consumo de energía, el cálculo del deslizamiento es útil para determinar qué tan rápido se realizará la operación. El deslizamiento excesivo también puede tener efectos adversos en la estructura del suelo e inhibir el crecimiento de las plantas.
Ejemplo\(\PageIndex{3}\)
Ejemplo 3: Fuerza de tracción y potencia
Problema:
Considere una rueda que funcione con una carga dinámica de 10 kN, una relación de resistencia al movimiento de 0.08 y una relación de tracción bruta de 0.72. Encuentra la fuerza de tracción que puede desarrollar la rueda. Si esta rueda gira a 40 rpm y el radio de rodadura de la rueda es de 0.71 m, ¿cuánta potencia es necesaria para mover esta rueda?
Solución
Calcule la fuerza de tracción bruta desarrollada por la rueda F usando la Ecuación 3.1.16:
\( F= \mu_{g} W = 0.72 \times 10 = 7.2 \text{ kN} \)
Calcule la resistencia al movimiento F r de esta rueda usando la Ecuación 3.1.17:
\( F_{r} = \rho W = 0.08 \times 10 = 0.80 \text{ kN} \)
La fuerza de tracción H desarrollada por la rueda, de acuerdo con la Ecuación 3.1.12, es la diferencia entre la fuerza de tracción bruta y la resistencia al movimiento:
\( H = F-F_{r} = 7.2 - 0.8 = 6.4 \text{ kN} \)
Calcule el par necesario para mover esta rueda usando la Ecuación 3.1.23:
\( T = Fr = 7.2 \times 0.71 = 5.11 \text{ kN m} \)
Calcula la potencia Pw necesaria para girar la rueda usando la Ecuación 3.1.1:
\( P_{W} = T \omega = T \frac{2\pi N}{60} = 5.11 \times \frac{2 \times \pi \times 40}{60} = 21.4 \text{ kW} \)
Ejemplo\(\PageIndex{4}\)
Ejemplo 4: Potencia bruta del volante del motor
Problema:
Calcule la potencia necesaria de un tractor MFWD para tirar de una sembradora de 30 hileras. De acuerdo con las Normas ASABE (2015), se requiere una fuerza de 900 N por fila para tirar de una sembradora de cultivos en hileras dibujadas si solo está realizando la operación de siembra. La velocidad del tractor será de 8.1 km h −1 (2.25 m s −1). El suelo se encuentra en estado labrado. Considera que el tractor debe tener una reserva de marcha del 20% para superar sobrecargas inesperadas.
Solución
Calcule la fuerza de la barra de tiro necesaria para tirar de la sembradora usando la Ecuación 3.1.25:
\( F_{p} = f_{r}n_{r} = 900 \times 30 = 27,000 \text{ N} \)
Calcule la potencia de la barra de tracción P DB necesaria para tirar de la sembradora usando la Ecuación 3.1.24:
\( P_{DB} = F_{p} \nu_{p} = 27,000 \times 2.25 = 60,750 \text{ W} \)
Por lo tanto, el tractor necesita producir una potencia de barra de tiro de 60.75 kW. De la Figura 3.1.5, encontrar que el coeficiente que relaciona la potencia de la barra de tracción con la potencia de PTO del tractor para un tractor MFWD que trabaja en condiciones de suelo labrado es de 0.72. Por lo tanto, el tractor PTO potencia P PTO debe ser:
\( P_{PTO} = \frac{P_{DB}}{0.72} = \frac{60.75}{0.72} = 84 \text{ kW} \)
Considerando que el coeficiente que relaciona la potencia de PTO con la potencia bruta del volante del motor es de 0.83 (Figura 3.1.5), la potencia bruta del volante del motor P e es:
\( P_{e} = \frac{P_{PTO}}{0.83} = \frac{84.375}{0.83} = 102 \text{ kW} \)
Considerando una reserva de potencia de 20% para superar sobrecargas inesperadas, el tractor seleccionado debe tener una potencia bruta del volante del motor al menos 20% mayor a la necesaria para tirar de la sembradora de 30 hileras, o 1.2 × 102 kW = 122 kW.
Estos cálculos ayudarán al gerente de la granja a seleccionar el tractor adecuado para la operación.
Créditos de imagen
Figura 1. Queiroz, D. (CC Por 4.0). (2020). Vista esquemática de un tractor agrícola con tracción en las dos ruedas.
Figura 2. Queiroz, D. (CC Por 4.0). (2020). Diagrama simplificado de las variables relacionadas con una rueda que desarrolla una fuerza de tracción neta.
Figura 3. Queiroz, D. (CC Por 4.0). (2020). Diagrama de las variables relacionadas con una rueda que desarrolla una fuerza de tracción neta (H) incluyendo la fuerza de tracción bruta (F) y la fuerza de resistencia al movimiento (F r).
Figura 4. Queiroz, D. (CC Por 4.0). (2020). Diagrama de fuerzas que actúan sobre una rueda remolcada.
Figura 5. Norma ASABE ASAE D497.7 (CC Por 4.0). (2020). Diagrama de las relaciones aproximadas de potencia en tractores agrícolas (los tipos se definen en el texto principal) y las condiciones del suelo.
Figura 6. Schueller, J. (CC Por 4.0). (2020). Tractores típicos contemporáneos (a) pequeños y (b) grandes.
Referencias
Estándares ASABE. (2018). ANSI/ASAE S296.5 DEC2003 (R2018): Terminología general para la tracción de dispositivos y vehículos agrícolas de tracción y transporte. San José, MI: ASABE.
Estándares ASABE. (2015). ASAE D497.7 MAR2011 (R2015): Datos de manejo de maquinaria agrícola. San José, MI: ASABE.
Goering, C. E., Stone, M. L., Smith, D. W., & Turnquist, P. K. (2003). Dispositivos de tracción y transporte. En principios de ingeniería de vehículos todoterreno (pp. 351-382). San José, MI: ASAE.
Kolator, B., & Białobrzewski, I. (2011). Un modelo de simulación de rendimiento de tractor 2WD. Comput. Electrón. Agric. 76 (2): 231-239.
Renius, K. T. (2020). Fundamentos del diseño de tractores. Cham, Suiza: Springer Nature.
SAE. (1995). SAE J1995_199506: Código de prueba de potencia del motor—Encendido por chispa e ignición por compresión—Potencia bruta nominal. Troy, MI: SAE.
Schueller, J. K. (2000). Al servicio de la abundancia: La mecanización agrícola proporcionó el alimento para el extraordinario crecimiento del siglo XX. Mech. Ing. 122 (8) :58-65.


