3.4: Mecatrónica y Sistemas Inteligentes en Maquinaria Agrícola
- Page ID
- 80895
Francisco Rovira-Más
Laboratorio de Robótica Agrícola, Universitat Politècnica de València, Valencia, España
Qin Zhang
Centro de Precisión y Sistemas Agrícolas Automatizados, Universidad Estatal de Washington, Prosser, Washington
Verónica Saiz-Rubio
Laboratorio de Robótica Agrícola, Universitat Politècnica de València, Valencia, España
| Términos Clave |
| Sistemas de control | Datos analógicos y digitales | Tractores autoguiados |
| Actuadores | Posicionamiento | Aplicación de tasa variable |
| Sensores | Visión e imagenología | Maquinaria inteligente |
Variables
Introducción
Los visitantes de las ferias agrícolas locales tienen una buena oportunidad de ver tractores viejos. Los visitantes curiosos notarán que los más antiguos, digamos, los realizados en las tres primeras décadas del siglo XX, son puramente mecánicos. A medida que los visitantes observan tractores más nuevos, pueden encontrar que en esas máquinas aparecieron componentes electrónicos y accionados por fluidos. Ahora, la maquinaria agrícola, como los tractores y las cosechadoras, son tan sofisticadas que están totalmente equipadas con controles electrónicos e incluso pantallas planas elegantes. Estos controles y pantallas son la interfaz del conductor con componentes electromecánicos integrados en tractores modernos.
El término mecatrónica se usa para referirse a sistemas que combinan controles de computadora, componentes eléctricos y partes mecánicas. Una solución mecatrónica no es solo la adición de sensores y electrónica a una máquina ya existente; más bien, es la integración equilibrada de todos ellos de tal manera que cada componente individual potencia el rendimiento de los demás. Este resultado se logra únicamente considerando todos los subsistemas simultáneamente en las primeras etapas del diseño (Bolton, 1999). Así, la mecatrónica unifica las tecnologías que subyacen a los sensores, los sistemas de control automático, los procesadores informáticos y la transmisión de energía a través de mecanismos que incluyen actuadores de potencia fluida.
Durante el siglo XX, la mecanización agrícola redujo en gran medida el trabajo pesado del trabajo agrícola al tiempo que aumentaba la productividad (más tierras cultivadas por menos personas), la eficiencia (menos tiempo y recursos invertidos para cultivar la misma cantidad de tierra) y la calidad del trabajo (pérdidas reducidas en la cosecha, aplicaciones químicas más precisas, logrando una labranza uniforme). La Revolución Verde, liderada por Norman Borlaug, incrementó la productividad al introducir variedades de cultivos adaptadas a la región y el uso de fertilizantes efectivos, lo que a menudo resultó en que los rendimientos se duplicaran, especialmente en los países en desarrollo. Con tales mejoras iniciadas por la Revolución Verde, la productividad actual, la eficiencia y los cultivos alimentarios de calidad pueden ser suficientes para apoyar a una población mundial en crecimiento proyectada para superar los 9.5 mil millones para 2050, pero el reto real es hacerlo de manera sustentable por medio de una agricultura regenerativa ( Myklevy et al., 2016). Este reto se complica aún más por la continua disminución de la fuerza laboral agrícola a nivel mundial.
La maquinaria agrícola actual, como tractores grandes, pulverizadores y cosechadoras combinadas, puede ser demasiado grande en la práctica porque deben recorrer caminos rurales, usar potentes motores diesel que están sujetos a regulaciones restrictivas de emisiones, son difíciles de automatizar por razones de responsabilidad y degradar el suelo agrícola al compactación de rueda alta. Estos retos, y muchos otros, pueden superarse mediante la adopción de tecnologías mecatrónicas y sistemas inteligentes en la maquinaria agrícola moderna. La agricultura mecanizada ha venido adoptando mayores niveles de automatización e inteligencia para mejorar la gestión y aumentar la productividad en las operaciones de campo. Por ejemplo, los agricultores de hoy en día pueden usar vehículos agrícolas autodirigidos para muchas operaciones de campo diferentes, incluyendo labranza, plantación, aplicaciones químicas y cosecha. Recientemente se ha introducido a los agricultores maquinaria inteligente para el raleo automático o el deshierbe preciso en hortalizas y otros cultivos.
Este capítulo introduce los conceptos básicos de mecatrónica y sistemas inteligentes utilizados en la maquinaria agrícola moderna, incluidos los robots agrícolas. En particular, introduce brevemente una serie de tecnologías centrales, componentes clave y desafíos típicos encontrados en escenarios agrícolas. El material presentado en este capítulo proporciona una introducción básica a la mecatrónica y las tecnologías inteligentes disponibles hoy en día para aplicaciones de producción de campo, y una idea del vasto potencial que estos enfoques tienen para mejorar la mecanización mundial de la agricultura en las próximas décadas.
Conceptos
El término mecatrónica se aplica a los sistemas de ingeniería que combinan computadoras, componentes electrónicos y partes mecánicas. El concepto de mecatrónica es la integración perfecta de estos tres subsistemas; su encarnación en un sistema único conduce a un sistema mecatrónico. Cuando el sistema mecatrónico está dotado de técnicas de inteligencia artificial, el sistema mecatrónico se clasifica además como un sistema inteligente, que es la base de robots y maquinaria agrícola inteligente.
Sistemas de Control Automático
La maquinaria basada en mecatrónica necesita contar con sistemas de control para implementar las funciones automatizadas que realicen las tareas designadas. Los sistemas mecatrónicos consisten en hardware electromecánico y software de control que codifica el algoritmo o modelo que automatiza una operación. Un sistema de control automático obtiene información relevante del entorno circundante para administrar (o regular) el comportamiento de un dispositivo que realiza las operaciones deseadas. Un buen ejemplo es un controlador de aire acondicionado (CA) doméstico que utiliza un termostato para determinar la desviación de la temperatura ambiente de un valor preestablecido y encender y apagar la CA para mantener el hogar a la temperatura preestablecida. Un ejemplo en maquinaria agrícola es la dirección automática. Supongamos que un pequeño tractor utilitario ha sido modificado para que se dirija automáticamente entre hileras de vides en un viñedo. Se puede utilizar una cámara mirando hacia el futuro para detectar la posición de las hileras de vid, de tal manera que las desviaciones del tractor desde la línea central entre las hileras de vid están relacionadas con el ángulo de dirección adecuado para guiar el tractor en el viñedo sin chocar contra una vid. De esos dos ejemplos, se puede observar que un sistema de control, en general, consiste en sensores para obtener información, un controlador para tomar decisiones, y un actuador para realizar las acciones que automatizan una operación.
La actuación que se basa en el seguimiento continuo de la variable bajo control (como la temperatura o el ángulo de la rueda) se denomina control de bucle cerrado y proporciona un rendimiento estable para la automatización. El control de bucle cerrado permite la estimación en tiempo real del error (que se define como la diferencia entre la salida deseada de la variable controlada y el valor real medido por un sensor de retroalimentación), y calcula un comando de corrección con una función de control, el controlador, para reducir el error. Este comando se envía al actuador (discutido en la siguiente sección) para implementar automáticamente la corrección. Esta función de controlador puede ser una simple proporción del error (controlador proporcional, P), una medida de la sensibilidad de cambio (controlador derivado, D), una función dependiente de errores acumulados (pasados) (controlador integral, I), o una combinación de dos o tres de las funciones mencionadas anteriormente (PD, PI, PID). Existen técnicas alternativas para implementar controles automatizados, como sistemas inteligentes que utilizan métodos de inteligencia artificial (IA) como redes neuronales, lógica difusa, algoritmos genéticos y aprendizaje automático para ayudar a tomar decisiones de control más similares a las humanas.
Actuadores
Un componente electromecánico es una parte integrada que recibe una señal eléctrica para crear un movimiento físico para accionar un dispositivo mecánico realizando una determinada acción. Los ejemplos de componentes electromecánicos incluyen motores eléctricos que convierten la corriente eléctrica de entrada en la rotación de un eje, y válvulas de modulación por ancho de pulso (PWM), como boquillas de velocidad variable y controladores de solenoide proporcionales, que reciben una señal eléctrica para empujar el carrete de un hidráulico válvula de control para ajustar la abertura de la válvula que controla la cantidad de fluido que pasa a través. Debido a que los sistemas de implementos hidráulicos son ampliamente utilizados en maquinaria agrícola, es común ver muchos más componentes electrohidráulicos (como controladores de solenoide proporcionales y servocontroladores) que motores eléctricos en máquinas agrícolas. Sin embargo, a medida que las soluciones robóticas se vuelven cada vez más disponibles en la agricultura, probablemente aumentarán las aplicaciones de motores eléctricos en maquinaria agrícola moderna, especialmente en versiones inteligentes y robóticas. El uso de componentes mecatrónicos sienta las bases para adoptar tecnologías de automatización a la maquinaria agrícola, incluyendo la conversión de máquinas tradicionales en máquinas robóticas capaces de realizar trabajos de campo de manera autónoma.
Maquinaria Agrícola Inteligente y Robots Agrícolas
Para que la maquinaria agrícola inteligente sea capaz de realizar operaciones de campo automatizadas, se requiere que las máquinas tengan la capacidad de: (1) tomar conciencia de las condiciones reales de operación; (2) determinar correcciones adaptativas adecuadas para condiciones que cambian continuamente; y (3) implementar tales correcciones durante las operaciones de campo, con el apoyo de un sistema mecánico adecuado. El núcleo para lograr tal capacidad a menudo descansa en los modelos que gobiernan la maquinaria inteligente, que van desde reglas lógicas simples que controlan tareas básicas hasta sofisticados algoritmos de IA para llevar a cabo operaciones complejas. Estos algoritmos de alto nivel se pueden desarrollar utilizando técnicas populares como redes neuronales artificiales, lógica difusa, razonamiento probabilístico y algoritmos genéticos (Russell y Norvig, 2003). Como muchas de esas máquinas inteligentes podrían realizar algunas tareas de campo de manera autónoma, como podría hacer un trabajador humano, dicha maquinaria también puede denominarse maquinaria robótica. Por ejemplo, cuando una cortadora de césped autónoma (Figura 3.4.1a) deambula dentro de un patio, normalmente está dotada de habilidades básicas de navegación y planificación de caminos que hacen que la cortadora encaje bien en la categoría de maquinaria robótica, y por lo tanto, es razonable considerarla un robot de campo. Aunque estas máquinas robóticas no están reemplazando actualmente a los trabajadores humanos en las operaciones de campo, la introducción de la robótica en la agricultura y su uso generalizado es solo cuestión de tiempo. La Figura 3.4.1b muestra un trasplantador de arroz autónomo (mejor llamado robot de trasplante de arroz) desarrollado por la Organización Nacional de Investigación Agrícola y Alimentaria (NARO) de Japón.
(a)
b)
Figura\(\PageIndex{1}\): a) Segadora autónoma (cortesía de John Deere); (b) Transplantadora de arroz autónoma basada en GPS (cortesía de NARO, Japón).
Muchas publicaciones financieras pronostican que habrá un rápido crecimiento del mercado de robots de servicio en las próximas dos décadas, y aquellos dentro de las aplicaciones agrícolas jugarán un papel importante. La Figura 3.4.2 muestra el crecimiento esperado del mercado estadounidense de robots agrícolas por tipo de producto. Aunque los robots de ordeño y manejo de lácteos han dominado el mercado de robots agrícolas en la última década, se espera que los robots de producción de cultivos aumenten su presencia comercialmente y lideren el mercado en los próximos años, particularmente para la producción de cultivos especiales (por ejemplo, frutos de árbol, uvas, melones, nueces, y verduras). Esta transformación del agricultor del siglo XXI de obrero a gerente de la era digital puede ser fundamental para atraer a las generaciones más jóvenes a carreras en la producción agrícola.
Sensores en Sistemas Mecatrónicos
Los sensores son una clase de dispositivos que miden parámetros significativos mediante el uso de una variedad de fenómenos físicos. Son componentes importantes en un sistema mecatrónico porque proporcionan la información necesaria para soportar operaciones automatizadas. Si bien los datos a medir pueden ser de muchas formas, los sensores emiten los datos medidos ya sea en formatos analógicos o digitales (descritos en la siguiente sección). En la maquinaria agrícola moderna, las salidas de los sensores eventualmente se transforman a formato digital y así pueden mostrarse en una pantalla LCD o alimentarse a una computadora. Esta alta conectividad entre sensores y computadoras ha acelerado la expansión de la automatización de maquinaria. Una máquina inteligente puede ayudar a los trabajadores humanos a realizar operaciones más eficientes: en algunos casos, simplemente implicará recuperar información más clara o mejor; en otros casos, incluirá la automatización de las funciones físicas. En casi todas las situaciones, se necesita la contribución de sensores confiables para que las máquinas interactúen con el entorno circundante. La Figura 3.4.3 muestra la arquitectura de un tractor inteligente, que incluye los sensores típicos a bordo de la maquinaria agrícola inteligente.
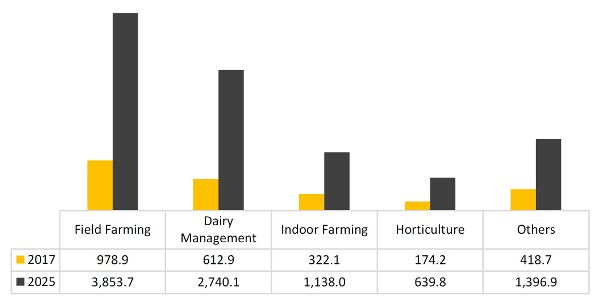
A pesar de que los sensores recopilan los datos necesarios para ejecutar una acción en particular, eso puede no ser suficiente porque el entorno de producción agrícola a menudo se complica por muchos factores. Por ejemplo, los cambios de iluminación a lo largo del día, las condiciones climáticas adversas pueden afectar el rendimiento de los sensores, y los campos abiertos están plagados de incertidumbre donde otras máquinas, animales, herramientas e incluso trabajadores pueden aparecer inesperadamente en las cercanías cercanas. Los datos detectados pueden ser insuficientes para soportar una operación automatizada segura, confiable y eficiente y, por lo tanto, las técnicas de procesamiento de datos son necesarias para obtener información más completa hasta que sea suficiente para soportar operaciones automatizadas. Como regla general, no hay ningún sensor que proporcione toda la información necesaria, y no hay ningún sensor que nunca falle. Dependiendo de las necesidades específicas, los ingenieros suelen utilizar redundancia o fusión de sensores para resolver dicho problema. El primero adquiere la misma información a través de fuentes independientes en caso de que una de ellas falle o disminuya su confiabilidad, y la segunda combina información de varias fuentes que son complementarias. Una vez que la información percibida ha sido procesada usando cualquiera de los dos métodos, el comando de accionamiento puede calcularse y luego ejecutarse para completar la tarea.
Datos analógicos y digitales
Como se mencionó anteriormente, los sistemas mecatrónicos a menudo utilizan sensores para obtener información para soportar operaciones automatizadas. Los sensores proporcionan mediciones de magnitudes físicas (por ejemplo, temperatura, velocidad, presión, distancia e intensidad de luz) representadas por una cantidad de variables eléctricas (como tensiones y corrientes). Estas cantidades a menudo se denominan datos analógicos y normalmente se expresan en base 10, el sistema de numeración decimal. En contraste, los dispositivos electrónicos como los controladores representan números en la base 2 (el sistema de numeración binaria o simplemente “binario”) adoptando la característica de encendido-apagado de la electrónica, con un valor numérico de 1 asignado al estado “on” y 0 asignado al estado “off”.
Un sistema binario utiliza una serie de dígitos, limitados a ceros o unos, para representar cualquier número decimal. Cada uno de estos dígitos representa un bit del número binario; un dígito binario se llama bit. El 1 más a la izquierda en el número binario 1001 se llama el bit más significativo (MSB), y el 1 más a la derecha es el bit menos significativo (LSB). Es una práctica común en informática romper números binarios largos en segmentos de 8 bits, conocidos como bytes. Hay una correspondencia uno a uno entre los números binarios y los números decimales. Por ejemplo, se puede usar un número binario de 4 bits para representar todos los enteros decimales positivos desde 0 (representados por 0000) hasta 15 (representados por 1111). La digitalización de señales consiste en encontrar esa correspondencia particular.
El proceso de transformar números binarios en números decimales y viceversa es sencillo para representar enteros decimales positivos. Sin embargo, los números negativos y de punto flotante requieren técnicas especiales. Si bien la transformación de datos entre dos formatos normalmente se realiza automáticamente, es importante conocer el concepto subyacente para una mejor comprensión de cómo se puede corregir, procesar, distribuir y utilizar la información en sistemas inteligentes de maquinaria. La resolución de los datos digitales depende del número de bits, de tal manera que más bits significa más precisión en la medición digitalizada. La ecuación 3.4.1 arroja la relación entre el número de bits (n) y el número resultante de niveles digitales disponibles para codificar la señal (L). Por ejemplo, usar 4 bits conduce a 2 4 = 16 niveles, lo que implica que una señal analógica entre 0 V y 2 V tendrá una resolución de 2/15 = 0.133 V; como resultado, no se detectarán cantidades por debajo de 133 mV usando números de 4 bits. Si es necesaria más precisión, la digitalización tendrá que usar números con más bits. Tenga en cuenta que la Ecuación 3.4.1 es una relación exponencial en lugar de lineal, y la cuantificación crece rápidamente con el número de bits. Siguiendo con el ejemplo anterior, 4 bits producen 16 niveles, pero 8 bits dan 256 niveles en lugar de 32, lo que en realidad corresponde a 5 bits.
\[ L=2^{n} \]
donde L = número de niveles digitales en el proceso de cuantificación
n = número de bits
Detección de posición
Un requisito básico para que los robots agrícolas y la maquinaria inteligente funcionen de manera adecuada, confiable y efectiva es conocer su ubicación en relación con el entorno circundante. Por lo tanto, las capacidades de posicionamiento son esenciales.
Sistemas Globales de Navegación por Satélite (GNSS)
Sistema Global de Navegación por Satélite (GNSS) es un término general que describe cualquier constelación de satélites que proporciona servicios de posicionamiento, navegación y sincronización (PNT) a nivel global o regional. Mientras que el Sistema de Posicionamiento Global (GPS) de Estados Unidos es el GNSS más prevalente, otras naciones están fildeando, o han enviado, sus propios sistemas para proporcionar capacidad PNT complementaria e independiente. Otros sistemas incluyen Galileo (Europa), GLONASS (Rusia), BeiDou (China), IRNS/NAVIC (India) y QZSS (Japón).
Cuando el Departamento de Defensa de Estados Unidos lanzó la tecnología GPS para uso civil en 2000, desencadenó el crecimiento de la navegación por satélite para vehículos todo terreno, incluida la maquinaria agrícola robótica. En la actualidad, la mayoría de los principales fabricantes de maquinaria agrícola incluyen sistemas de asistencia a la navegación entre sus productos avanzados. A partir de 2019, solo el GPS (USA) estaba en pleno funcionamiento, pero la última generación de receptores ya puede expandir la constelación GPS con otros satélites GNSS.
Los receptores GPS emiten datos a través de un puerto serie enviando una serie de bytes codificados en un formato estándar que ha ganado aceptación general: NMEA 0183. El estándar de interfaz NMEA 0183 fue creado por la Asociación Nacional de Electrónica Marina de los Estados Unidos (NMEA), y consiste en mensajes GPS en formato de texto (ASCII) que incluyen información sobre la hora, la posición en coordenadas geodésicas (es decir, latitud (λ), longitud (φ) y altitud (h)), velocidad y precisión de la señal. El Sistema Geodésico Mundial 1984 (WGS 84), desarrollado por el Departamento de Defensa de Estados Unidos, define un elipsoide de revolución que modela la forma de la tierra, y sobre el cual se definen las coordenadas geodésicas. Adicionalmente, el WGS 84 define un sistema de coordenadas cartesianas fijado a la tierra y con su origen en el centro de masa de la tierra. Este sistema es el sistema de coordenadas fijas a la tierra centrado en la tierra (ECEF), y proporciona una forma alternativa de ubicar un punto en la superficie terrestre con las tres coordenadas cartesianas convencionales X, Y y Z, donde el eje Z coincide con el eje de rotación de la tierra y por lo tanto cruza la tierra polos.
La mayoría de las aplicaciones desarrolladas para maquinaria agrícola, sin embargo, no requieren cubrir grandes superficies en un corto período de tiempo. Por lo tanto, la curvatura de la tierra tiene un efecto insignificante, y la mayoría de los campos agrícolas pueden considerarse planos para fines prácticos. A menudo se usa un sistema de coordenadas de plano tangente local (LTP), también conocido como coordenadas NED, para facilitar operaciones a pequeña escala con coordenadas globales intuitivas norte (N), este (E) y abajo (D). Estas coordenadas se definen a lo largo de tres ejes ortogonales en una configuración cartesiana generada ajustando un plano tangente a la superficie de la tierra en un punto arbitrario seleccionado por el usuario y establecido como origen LTP. Dado que los receptores estándar proporcionan coordenadas geodésicas (λ, φ, h) pero las operaciones prácticas de campo requieren un marco local como LTP, una operación fundamental para aplicaciones de mapeo en agricultura es la transformación en tiempo real entre los dos sistemas de coordenadas ( Rovira-Más et al., 2010). Las ecuaciones 3.4.2 a 3.4.8 proporcionan el procedimiento paso a paso para lograr esta transformación.
\[ a = 6378137 \]
\[ e = 0.0818 \]
\[ N_{0}(\lambda)=\frac{a}{\sqrt{1-e^{2} \cdot sin^{2}\lambda}} \]
\[ X=(N_{0}+h) \cdot cos\lambda \cdot cos\phi \]
\[ Y=(N_{0}+h) \cdot cos\lambda \cdot sin\phi \]
\[ Z=[h+N_{0} \cdot (1-e^{2})] \cdot sin\lambda \]
\[ \begin{bmatrix} N \\E\\D \end{bmatrix} = \begin{bmatrix} -sin \lambda \cdot cos\phi & -sin\lambda \cdot sin\phi & cos\lambda \\ -sin\phi &cos\phi & 0 \\ -cos\lambda \cdot cos\phi & -cos\lambda \cdot sin\phi & -sin\lambda \end{bmatrix} \cdot \begin{bmatrix} X-X_{0} \\ Y-Y_{0} \\ Z-Z_{0} \end{bmatrix} \]
donde a = semieje mayor del elipsoide de referencia WGS 84 (m)
e = excentricidad del elipsoide de referencia WGS 84
N 0 = longitud de la normal (m)
Coordenadas geodésicas:
λ = latitud (°)
φ = longitud (°)
h = altitud (m)
(X, Y, Z) = Coordenadas ECEF (m)
(X 0, Y 0, Z 0) = origen definido por el usuario de coordenadas en formato ECEF (m)
(N, E, D) = coordenadas LTP norte, este, abajo (m)
A pesar de la alta accesibilidad de la información GPS, el posicionamiento basado en satélites se ve afectado por una variedad de errores, algunos de los cuales no se pueden eliminar por completo. Afortunadamente, una serie de errores importantes pueden compensarse mediante el uso de una técnica conocida como corrección diferencial, disminuyendo los errores de más de 10 m a aproximadamente 3 m. Además, el caso especial de correcciones diferenciales cinemáticas en tiempo real (RTK) puede disminuir aún más el error a solo nivel de centímetro.
Sensores de Sonar
Además de ubicar máquinas en campo, otra necesidad esencial de posicionamiento para los robots agrícolas es encontrar la posición de los objetos circundantes durante las operaciones agrícolas, como plantas objetivo u obstáculos potenciales. Los telémetros ultrasónicos son dispositivos de detección utilizados con éxito para este propósito. Debido a que miden la distancia de los objetos objetivo en términos de la velocidad del sonido, estos sensores también se conocen como sensores de sonar.
El principio subyacente de los sonares es que se conoce la velocidad del sonido (343 m s −1 a 20°C), y medir el tiempo que la onda necesita para golpear un obstáculo y regresar al sensor —el eco— permite estimar la distancia de un objeto. La velocidad del sonido a través del aire, V, depende de la temperatura ambiente, T, como:
\[ V(m\ s^{-1})=331.3 + 0.606 \times T(^\circ C) \]
La temperatura ambiente continuamente cambiante en los campos agrícolas es uno de los muchos desafíos para los sensores de sonar. Otro reto es la diversidad de objetos objetivo. En la práctica, los sensores de sonar deben enviar ondas sonoras que golpeen un objeto y luego regresar al receptor del sensor. Este receptor debe entonces capturar la señal para medir el tiempo transcurrido para que las olas completen el viaje de ida y vuelta. Comprender las limitaciones que plantean las propiedades reflectantes de los objetos objetivo es esencial para obtener resultados confiables. La distancia a los materiales que absorben las ondas sonoras, como los peluches, se medirá mal, mientras que los blancos sólidos y densos permitirán que el sistema funcione bien. Cuando el objeto objetivo es desigual, como marquesinas de cultivos, las mediciones pueden volverse ruidosas. Además, las ondas sonoras no se comportan como haces lineales, sino que se propagan en conos irregulares que se expanden en cobertura con la distancia. Cuando los objetos están fuera del cono, pueden no ser detectados. Los errores a menudo variarán con rangos de tal manera que rangos más lejanos conducen a errores más grandes.
Una característica de diseño importante a considerar es la distancia entre los sensores ultrasónicos adyacentes, ya que la interferencia de eco es otra fuente de comportamiento inestable. En general, los telémetros de sonar son útiles para estimar distancias cortas de manera rentable cuando la precisión y la confiabilidad no son críticas, como cuando se detectan distancias al dosel de los árboles para la pulverización automatizada de pesticidas.
Sensores de detección y alcance de luz (Lidar)
Otro sensor común de detección de posición es LIDAR, que significa detección de luz y rango. Los Lidars son dispositivos ópticos que detectan la distancia a los objetos objetivo con precisión. Aunque se pueden usar diferentes fuentes de luz para estimar rangos, la mayoría de los dispositivos LIDAR utilizan pulsos láser porque su densidad de haz y coherencia dan como resultado una alta precisión.
Los lidars poseen características específicas que los hacen favorables para aplicaciones robóticas de campo, ya que la luz solar no afecta a los lidares a menos que golpee directamente a su emisor, y funcionan excelentemente bajo poca iluminación.
Sensores de visión artificial y de imagen
Un elemento importante de la inteligencia humana es la visión, que da a los agricultores la capacidad de percepción visual. Un requisito básico para la maquinaria agrícola inteligente (o robots agrícolas) es tener la capacidad de conciencia circundante. La visión artificial es la versión informática de la vista del agricultor; las cámaras funcionan como ojos y las computadoras como el cerebro. Los datos de salida de los sistemas de visión son imágenes digitales. Una imagen digital consiste en pequeños cuadrados llamados píxeles (elementos de imagen) que transportan información sobre su nivel de intensidad de luz. La mayoría de las cámaras digitales utilizadas en los robots agrícolas son CCD (dispositivos de carga acoplada), las cuales están compuestas por un pequeño sensor rectangular hecho de una cuadrícula de diminutas celdas sensibles a la luz, cada una de ellas produciendo la información de su píxel correspondiente en la imagen. Si la imagen está en blanco y negro (técnicamente llamada monocromática), el nivel de intensidad se representa en una escala de grises entre un valor mínimo (0) y un valor máximo (i max). El número de niveles en la escala de grises depende del número de bits en los que se codifica la imagen. La mayoría de las imágenes utilizadas en agricultura son de 8 bits, lo que significa que la imagen puede distinguir 256 niveles de gris (2 8), donde el valor mínimo es 0 representando negro completo, y el valor máximo es 255 representando blanco puro. En términos prácticos, los ojos humanos no pueden distinguir tantos niveles, y 8 bits son muchas veces más que suficientes. Cuando las imágenes digitales reproducen una escena en color, los píxeles llevan información de los niveles de intensidad para los tres canales de rojo (R), verde (G) y azul (B), lo que lleva a imágenes RGB. El procesamiento de las imágenes RGB es más complicado que las imágenes monocromáticas y queda fuera del alcance de este capítulo.
Las cámaras monoculares (que tienen una lente) constituyen sistemas de visión simples, sin embargo, la información que recuperan es poderosa. Al seleccionar una cámara, los ingenieros deben elegir parámetros técnicos importantes como la distancia focal de la lente, el tamaño del sensor y los filtros ópticos cuando hay rangos espectrales (colores) que deben bloquearse de la imagen. La distancia focal (f) está relacionada con el alcance de la escena que encaja en la imagen, y se define en la Ecuación 3.4.10. La relación geométrica descrita por la Figura 3.4.4 y la Ecuación 3.4.11 determina el campo de visión resultante (FOV) de cualquier escena dada. El diseño de un sistema de visión artificial, por lo tanto, debe incluir los parámetros adecuados de cámara y lente para asegurar que se cubra el FOV necesario y que los objetos objetivo estén enfocados en las imágenes.
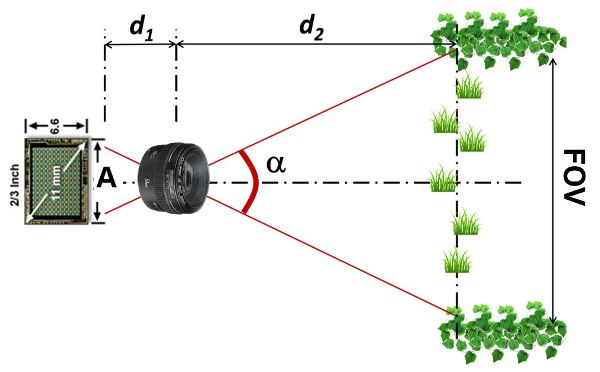
\[ \frac{1}{f} = \frac{1}{d_{1}}+\frac{1}{d_{2}} \]
\[ \frac{d_{1}}{d_{2}} = \frac{A}{FOV} \]
donde f = distancia focal del objetivo (mm)
d 1 = distancia entre el sensor de imagen y el centro óptico de la lente (mm)
d 2 = distancia entre el centro óptico de la lente y el objeto objetivo (mm)
A = dimensión horizontal del sensor de imagen (mm)
FOV = campo de visión horizontal cubierto en las imágenes (mm)
Después de tomar las imágenes, se completa el primer paso del proceso (adquisición de imágenes). El segundo paso, el análisis de las imágenes, comienza con el procesamiento de imágenes, lo que implica la delicada tarea de extraer la información útil de cada imagen para su posterior uso. La Figura 3.3.5 reproduce los resultados de un algoritmo de segmentación basado en el color para encontrar la posición de las mandarinas en un árbol de cítricos.
A pesar de que las imágenes digitales reproducen escenas con gran detalle, la representación es plana, es decir, en dos dimensiones (2D). Sin embargo, las escenas reales están en tres dimensiones (3D), siendo la tercera dimensión la profundidad, o distancia entre la cámara y los objetos de interés en la escena. En la imagen mostrada en la Figura 3.3.5, por ejemplo, se puede ubicar una naranja específica con precisión en los ejes horizontal y vertical, pero no se puede conocer qué tan lejos está del sensor. Esta información sería esencial, por ejemplo, para programar un brazo robótico para recuperar las naranjas. Las cámaras estéreo (que son cámaras con al menos dos lentes que cumplen con los principios de la estereoscopía) permiten la adquisición de dos (o más) imágenes en una determinada posición relativa a la que se aplican los principios de la visión estereoscópica. Estos principios imitan cómo funciona la visión humana, ya que las imágenes capturadas por los ojos humanos en las retinas están ligeramente compensadas, y este desplazamiento (conocido como disparidad) es lo que permite al cerebro estimar la profundidad.
Estimación de los Estados Dinámicos del Vehículo
Los parámetros que ayudan a comprender el comportamiento dinámico de un vehículo se conocen como estados del vehículo y, por lo general, incluyen velocidad, aceleración, desplazamiento lateral y tasas angulares de guiñada, cabeceo y balanceo. Los sensores necesarios para tales mediciones se ensamblan comúnmente en un sensor de movimiento compacto llamado unidad de medición inercial (IMU), creado a partir de una combinación de acelerómetros y giroscopios. Los acelerómetros de la IMU detectan la aceleración como el cambio en la velocidad del vehículo a lo largo del tiempo. Una vez conocida la aceleración, su integración matemática da una estimación de la velocidad, y la integración de nuevo da una estimación de la posición. La ecuación 3.4.12 permite el cálculo de velocidades instantáneas a partir de las mediciones de aceleración de una IMU o de cualquier acelerómetro individual. Observe que para incrementos finitos de tiempo ∆t, la función integral es reemplazada por una suma. De manera similar, los giroscopios pueden detectar las velocidades angulares del vehículo de giro; la integración de estos valores conduce a ángulos de balanceo, cabeceo y guiñada, como se especifica en la Ecuación 3.4.13. Un IMU típico está compuesto por tres acelerómetros y tres giroscopios ensamblados a lo largo de tres ejes perpendiculares que reproducen un sistema de coordenadas cartesianas. Con esta configuración física, es posible calcular los tres componentes de aceleración y velocidad en coordenadas cartesianas así como ángulos de Euler balanceo, cabeceo y guiñada. Las IMU actuales en el mercado son pequeñas y económicas, favoreciendo la estimación precisa de los estados de los vehículos con pequeños dispositivos como los sistemas microelectromecánicos (MEMS).
donde V t = velocidad de un vehículo en el tiempo t (m s −1)
a t = aceleración lineal registrada por un acelerómetro (o IMU) en el tiempo t (m s −2)
Δ t = intervalo de tiempo entre dos mediciones consecutivas
\(\Theta_{t}\)= ángulo en el tiempo t (rad)
\(\dot{\Theta}\)= velocidad angular en el tiempo t medida por un giroscopio (rad s −1)
Aplicaciones
Sistemas Mecatrónicos en Tractores Autoguiados
Como se mencionó a principios de este capítulo, los sistemas mecatrónicos están jugando ahora un papel esencial en la maquinaria agrícola moderna, especialmente en vehículos inteligentes y robóticos. Por ejemplo, los primeros tractores autoguiados llegaron al mercado a principios del siglo XXI; desde el punto de vista de la navegación, los fabricantes de equipos agrícolas han estado aproximadamente dos décadas por delante de la industria automotriz. Dichos tractores autoguiados no serían posibles si no se hubieran actualizado a sistemas mecatrónicos de última generación, que incluyen elementos de detección, control y accionamiento electromecánico (o electrohidráulico). Uno de los componentes más representativos nunca antes vistos en tractores mecánicos convencionales como elemento integrado es el receptor GPS de alta precisión, que proporciona a los tractores la capacidad de localizarse para guiarlos siguiendo caminos designados.
Las primeras soluciones de navegación que estaban disponibles comercialmente no controlaban realmente el sistema de dirección del tractor; más bien, proporcionaban a los tractores correcciones laterales en tiempo real, de tal manera que al seguir estas correcciones el vehículo rastreaba fácilmente una trayectoria predefinida. Este enfoque es fácil de aprender y ejecutar, ya que los conductores solo necesitan seguir un indicador de barra de luces, donde el número de luces encendidas es proporcional a la corrección lateral para mantener el vehículo en la pista. Además de su simplicidad de uso, este sistema funciona para cualquier máquina agrícola, incluidas las más antiguas. La Figura 3.4.6a muestra un sistema de barras de luz montado en un tractor de huerto, donde la luz roja indica al usuario que realice una corrección inmediata para permanecer dentro de la trayectoria mostrada en la pantalla LCD.
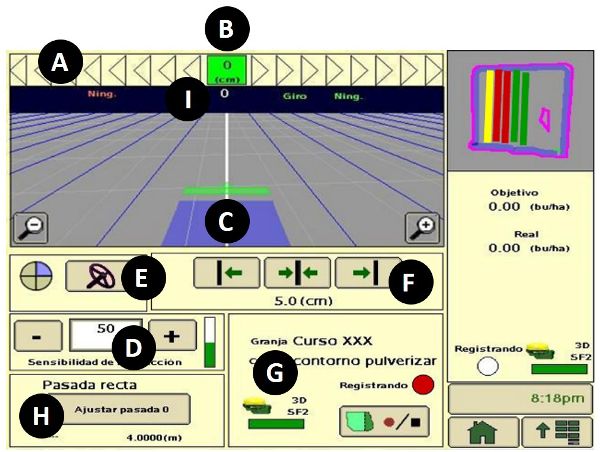
Otra mejora esencial de los tractores modernos basados en la tecnología mecatrónica es el sistema electrohidráulico que permite que los tractores sean maniobrados por alambre. Esto significa que una operación del tractor, como dirigir o bajar el implemento instalado en el enganche de tres puntos, se puede lograr mediante un sistema de accionamiento electrohidráulico controlado electrónicamente en respuesta a las señales de control generadas por un controlador basado en computadora. Un sistema de dirección electrohidráulico permite que un tractor sea guiado automáticamente, mediante la ejecución de comandos de navegación calculados por una computadora de a bordo en función de las señales de posicionamiento GPS recibidas. Una popular aplicación de autodirección se conoce como seguimiento paralelo, que permite que un tractor que se conduce automáticamente siga las vías deseadas en paralelo a una línea de referencia entre dos puntos, digamos la línea A-B, en un campo registrado por el sistema GPS a bordo. Estas líneas de referencia pueden incluso incluir sectores curvos. La Figura 3.4.6b muestra la pantalla de control de un sistema de autoguiado comercial implementado en un tractor tipo rueda. Observe que la magnitud de la desviación del tractor (el error fuera de pista) de la trayectoria predefinida se muestra en la barra superior, de manera similar a las correcciones transportadas a través de barras de luz. La implementación de la guía automática ha reducido las superposiciones paso a paso, especialmente con equipos grandes, lo que resulta en ahorros significativos en semillas, fertilizantes y productos químicos fitosanitarios, así como una reducción de la fatiga del operador. Los agricultores están viendo retornos de la inversión en apenas unos años.
(a)
b)
Figura Sistemas de\(\PageIndex{6}\): guía automática: (a) Kit de barra de luz; (b) Pantalla de control de seguimiento paralelo, donde A es el indicador de precisión de ruta, B es el error fuera de pista, C representa el icono de guía, D proporciona la sensibilidad de dirección, E ordena encendido/apagado de dirección, F localiza los botones de pista de cambios, G es el Indicador de estado GPS, H es el botón de seguimiento A-B (0) y I muestra el número de pista.
Control Automático de Aplicaciones de Velocidad Variable
La idea de aplicación de tasa variable (VRA) es aplicar la cantidad correcta de insumos, es decir, semillas, fertilizantes y pesticidas, en el momento adecuado y con precisión de subparcela, alejándose de las tasas promedio por parcela que resultan en pérdidas económicas y amenazas ambientales. La mecatrónica permite la implementación práctica de VRA para agricultura de precisión (PA). En términos generales, los equipos VRA de última generación requieren tres componentes mecatrónicos clave: (1) sensores, (2) controladores y (3) actuadores.
La precisión de la subparcela es factible con receptores GPS que proporcionan la posición instantánea de los equipos agrícolas en una ubicación específica dentro de un campo. Además, los vehículos requieren el soporte de un controlador de aplicaciones automatizado para entregar la cantidad exacta de producto. La cantidad específica de producto a aplicar en cada ubicación es comúnmente proporcionada por un mapa de prescripción precargado en la computadora del vehículo, o alternativamente, estimado en tiempo real usando sensores de salud de cultivos a bordo.
Existen sensores específicos que deben formar parte de las máquinas VRA. Por ejemplo, para que los pulverizadores inteligentes sean capaces de adaptar automáticamente la tasa de pesticida a las propiedades de los árboles, se requiere un posicionamiento global y local en campo o relacionado con los cultivos. Los fertilizantes, por otro lado, pueden beneficiarse de mapas de parámetros del suelo (humedad, materia orgánica, nutrientes), así como de la vegetación (vigor, estrés, malezas, temperatura). En muchos pulverizadores modernos, la presión y el flujo de los recursos aplicados (ya sean líquidos o gaseosos) deben ser rastreados para soportar el control automático y eventualmente lograr una tasa de aplicación precisa. Los controladores son los dispositivos que calculan la tasa óptima de aplicación sobre la marcha y proporcionan inteligencia al sistema mecatrónico. A menudo consisten en microcontroladores que leen mediciones de sensores o mapas cargados para calcular la tasa instantánea de aplicación del producto en base a algoritmos internos. Esta tasa se envía continuamente a los actuadores para la aplicación física del producto. Los controladores pueden incluir pequeñas pantallas de monitoreo o interruptores para el accionamiento manual desde la cabina del operador, si es necesario. Los actuadores son dispositivos electromecánicos o electrohidráulicos que reciben señales eléctricas de los controladores para regular la cantidad de producto a aplicar. Esta regulación generalmente se logra variando la velocidad de rotación de una bomba, modificando el flujo proveniente de un tanque, o cambiando los ajustes de una válvula para ajustar la presión o flujo del producto. Cambiar la presión de los líquidos rociados, sin embargo, da como resultado un cambio en el tamaño de la gota, lo cual no es deseable para el control de plagas. En estos casos, se recomienda el uso de boquillas inteligentes que se controlan a través de señales PWM.
A medida que la tecnología VRA avanza rápidamente, los aplicadores inteligentes están llegando a estar disponibles comercialmente, principalmente para cultivos básicos. Un sistema inteligente puede ajustar automáticamente la cantidad de insumos dispersos en respuesta a las necesidades, incluso permitiendo el uso simultáneo de varios tipos de tratamientos, dando como resultado nuevas formas de manejo de la producción agrícola. Por ejemplo, una sembradora inteligente de VRA tiene la capacidad de cambiar el número de semillas plantadas en el suelo de acuerdo con el potencial del suelo, ya sea proporcionada por mapas de prescripción o detectadas usando sensores a bordo. El control de la velocidad de siembra se logra accionando la abertura del dispositivo de distribución para permitir que pase el número deseado de semillas.
En muchos casos, se requiere un sistema de control de retroalimentación para lograr un control preciso de la tasa de aplicación. Por ejemplo, al aplicar productos químicos líquidos, la tasa de aplicación puede verse afectada por cambios en la velocidad de movimiento del vehículo, así como por las condiciones ambientales. Algunos pulverizadores inteligentes están programados para controlar con precisión la cantidad de líquido químico ajustando las boquillas en respuesta a los cambios de velocidad de avance del pulverizador. Esto normalmente se logra usando válvulas de boquilla controladas electrónicamente que se ordenan desde el procesador a bordo. Dicho sistema mecatrónico podría monitorear adicionalmente la presión del sistema y el flujo en el circuito de distribución con un receptor GPS, e incluso compensar los cambios de la cantidad de líquido que sale de las boquillas resultantes de los cambios de presión o patrón de flujo en el circuito.
Rediseño de un sistema de dirección de tractor con componentes electrohidráulicos
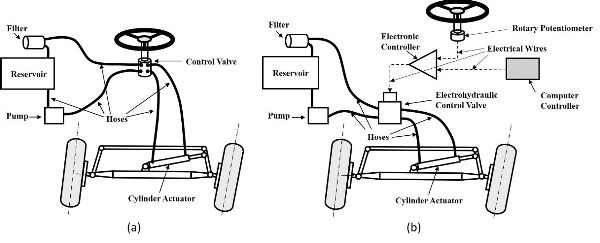
La implementación de capacidades de guía automática en un tractor requiere que el sistema de dirección se pueda controlar eléctricamente para el giro automatizado de las ruedas delanteras. Por lo tanto, es necesario reemplazar un sistema de dirección hidráulica tradicional por un sistema electrohidráulico. Esto podría lograrse simplemente reemplazando una válvula convencional de control de dirección accionada manualmente (Figura 3.4.7a) por un sistema de control electrohidráulico. Dicho sistema (Figura 3.4.7b) consiste en un potenciómetro giratorio para rastrear el movimiento del volante, un controlador electrónico para convertir la señal de dirección en una señal de control y una válvula de control electrohidráulica accionada por solenoide para implementar la señal de control entregada.
El sistema de dirección electrohidráulico mejorado puede recibir señales de control de un controlador de computadora habilitado para crear comandos de dirección apropiados en términos de salidas de un sistema autoguiado, haciendo posible la navegación sin la entrada de conductores humanos para lograr operaciones autónomas con el tractor. Como los componentes principales de un sistema electrohidráulico están conectados por cables, dicha operación también se llama “accionamiento por cable”.
Uso de sensores ultrasónicos para rangos de medición
La maquinaria agrícola a menudo necesita ser “consciente” de la posición de los objetos en las proximidades de las operaciones agrícolas, así como de la posición de la maquinaria. Los sensores ultrasónicos se utilizan a menudo para realizar tales mediciones.
Para utilizar un sensor ultrasónico (o sonar), a menudo se necesita un microprocesador para convertir las señales analógicas (que están en el rango de 0-5 V) del sensor ultrasónico a señales digitales, de modo que los datos registrados puedan ser utilizados adicionalmente por otros componentes de maquinaria automatizada o robótica. Por ejemplo, considere el HC-SR04, que consiste en un emisor de sonido y un receptor de eco de tal manera que mide el tiempo transcurrido entre una onda de sonido que es enviada por el emisor y su retorno desde el objeto objetivo. La velocidad del sonido es de aproximadamente 330 m·s −1, lo que significa que necesita 3 s para que el sonido viaje 1,000 m. El sensor HC-SR04 puede medir rangos de hasta 4.0 m, de ahí que las mediciones de tiempo sean del orden de milisegundos y microsegundos para rangos muy cortos. El sonido debe viajar por el aire, y la velocidad del sonido depende de las condiciones ambientales, principalmente de la temperatura ambiente. Si este sensor se usa en un caluroso día de verano con una temperatura promedio de 35°C, por ejemplo, usando la Ecuación 3.4.9, la velocidad del sonido corregida será ligeramente superior, a 352 m·s −1.
La Figura 3.4.8 muestra cómo el sensor fue conectado y alimentado por un producto comercial (microprocesador Arduino Uno, para fines ilustrativos) en una configuración de laboratorio (también para ilustración). Después de completar todo el cableado del sistema como se muestra en la Figura 3.4.8, es necesario seleccionar un puerto USB no utilizado y cualquiera de las velocidades por defecto en baudios en la computadora de interfaz. Si la velocidad en baudios y el puerto serie se configuran correctamente en una computadora con una consola de visualización, y los rangos medidos se han establecido mediante software a una frecuencia de actualización de 1 Hz, el sistema podría realizar una medición por segundo. Después de configurar el sistema, es importante verificar su precisión y robustez moviendo el objeto objetivo en el espacio por delante del sensor.
Ejemplos
Ejemplo\(\PageIndex{1}\)
Ejemplo 1: Digitalización de señales analógicas
Problema:
Los sistemas mecatrónicos requieren sensores para monitorear el desempeño de las operaciones automatizadas. Los sensores analógicos se utilizan comúnmente para tales tareas. Un mecanismo de dirección basado en mecatrónica utiliza un potenciómetro lineal para estimar el ángulo de dirección de un tractor autoguiado, emitiendo una señal analógica en voltios a medida que giran las ruedas delanteras. Para que los datos adquiridos sean utilizables por un sistema computarizado para automatizar la dirección, es necesario convertir los datos analógicos a formato digital.
Dada la señal analógica proveniente de un potenciómetro de dirección, digitaliza la señal usando 4 bits de resolución, mediante estos pasos.
- 1. Calcular el número de niveles codificados por la señal de 4 bits teniendo en cuenta que la tensión mínima emitida por el potenciómetro es de 1.2 V y la tensión máxima está limitada a 4.7 V, es decir, cualquier lectura proveniente del potenciómetro pertenecerá al intervalo 1.2 V—4.7 V. Cuantos pasos comprenden este digital señal?
- 2. Establecer una correspondencia entre las lecturas analógicas dentro del intervalo y cada nivel digital de 0000 a 1111, redactando una tabla para reflejar la correlación entre señales.
- 3. Trace ambas señales superpuestas para representar gráficamente el efecto de digitalizar una señal y la pérdida de precisión detrás del proceso. Según la trama, ¿cuál sería el valor digital correspondiente a una lectura de potenciómetro de 4.1 V?
Solución
El potenciómetro lineal tiene una varilla cuya posición varía desde la retracción (1.2 V) hasta la extensión completa (4.7 V). Cualquier posición de la varilla entre ambos extremos corresponderá a un voltaje en el rango 1.2 V—4.7 V. El número de niveles L codificados en la señal para n = 4 bits se calcula usando la Ecuación 3.4.1:
\( L=2^{n}=2^{4} = \textbf{16 levels} \)
Así, el número de pasos entre el número digital más bajo 0000 y el 1111 más alto es de 15 intervalos. La Tabla 3.4.1 especifica cada valor digital codificado por la señal de 4 bits, teniendo en cuenta que el tamaño de cada intervalo ∆V se establece por:
| Bit | Señal digital de 4 bits | Equivalencia analógica (V) | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
|
1 |
1 |
1 |
1 |
1 1 1 |
4.70000 |
|
0 |
1 1 0 |
4.46666 |
|||
|
0 |
1 |
1 1 0 1 |
4.23333 |
||
|
0 |
1 1 0 |
4.00000 |
|||
|
0 |
1 |
1 |
1 0 1 1 |
3.76666 |
|
|
0 |
1 0 1 0 |
3.53333 |
|||
|
0 |
1 |
1 0 0 1 |
3.30000 |
||
|
0 |
1 0 0 |
3.06666 |
|||
|
0 |
1 |
1 |
1 |
0 1 1 1 |
2.83333 |
|
0 |
0 1 1 0 |
2.60000 |
|||
|
0 |
1 |
0 1 0 1 |
2.36666 |
||
|
0 |
0 1 0 |
2.13333 |
|||
|
0 |
1 |
1 |
0 0 1 1 |
1.90000 |
|
|
0 |
0 0 1 0 |
1.66666 |
|||
|
0 |
1 |
0 0 0 1 |
1.43333 |
||
|
0 |
0 0 0 |
1.20000 |
|||
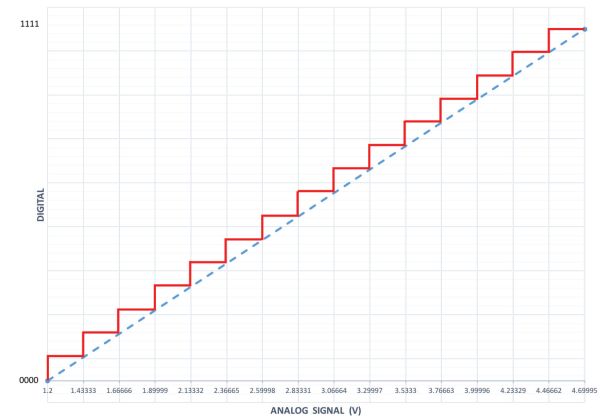
\( \Delta V = (4.7 - 1.2)/15 = 3.5/15 = 0.233 V \)
Una lectura de potenciómetro de 4.1 V pertenece al intervalo entre [4.000, 4.233], es decir, mayor o igual a 4 V e inferior a 4.233 V, que de acuerdo con la Tabla 3.4.1 corresponde a 1101. Las diferencias por debajo de 233 mV no se registrarán con una señal de 4 bits. Sin embargo, al aumentar el número de bits, el error disminuirá y el perfil de “escalera” de la Figura 3.4.9 se acercará cada vez más a la línea recta uniendo 1.2 V y 4.7 V.
Ejemplo\(\PageIndex{2}\)
Ejemplo 2: Transformación de coordenadas GPS
Problema:
Un robot de topografía utiliza un receptor GPS para localizar puntos de muestreo que forman una cuadrícula en un campo. Estos puntos constituyen la base de referencia para varias aplicaciones agrícolas de precisión relacionadas con la distribución espacial de las propiedades del suelo como la compacidad, el pH y el contenido de humedad. Los datos de ubicación (Cuadro 3.4.2) proporcionados por el receptor GPS están en un formato de código NMEA estándar. Transformar los datos (es decir, las coordenadas geodésicas proporcionadas por un receptor GPS portátil) al marco del plano tangente local (LTP) para que sean más directamente útiles para los agricultores.
Solución
El primer paso en el proceso de transformación requiere la selección de un elipsoide de referencia. Elija el elipsoide de referencia WGS 84 porque es ampliamente utilizado para aplicaciones agrícolas. Utilice las Ecuaciones 3.4.2 a 3.4.7 y aplique la función de transformación (Ecuación 3.4.8) a los 23 puntos dados en coordenadas geodésicas (Cuadro 3.4.2) para convertirlos en coordenadas LTP. Para ese elipsoide de referencia,
\( a = \text{semi-major axis of WGS 84 reference ellipsion} = 6378137\ m \)
\( e = \text{eccentricity of WGS 84 reference ellipsion} = 0.0818 \)
\( N_{0}(\lambda) = \frac{a}{\sqrt{1-e^{2} \cdot sin^{2}\lambda}} \)(Ecuación\(\PageIndex{4}\))
\( (N_{0}+h) \cdot cos\lambda \cdot cos\phi \)(Ecuación\(\PageIndex{5}\))
\( Y= (N_{0}+h) \cdot cos\lambda \cdot sin\phi \)(Ecuación\(\PageIndex{6}\))
\( Z = [h+N_{0} \cdot (1-e^{2})] \cdot sin\lambda \)(Ecuación\(\PageIndex{7}\))
\( \begin{bmatrix} N \\E\\D \end{bmatrix} = \begin{bmatrix} -sin \lambda \cdot cos\phi & -sin\lambda \cdot sin\phi & cos\lambda \\ -sin\phi &cos\phi & 0 \\ -cos\lambda \cdot cos\phi & -cos\lambda \cdot sin\phi & -sin\lambda \end{bmatrix} \cdot \begin{bmatrix} X-X_{0} \\ Y-Y_{0} \\ Z-Z_{0} \end{bmatrix} \)(Ecuación\(\PageIndex{8}\))
La longitud de la normal N 0 es la distancia desde la superficie del elipsoide de referencia hasta su intersección con el eje de rotación y [λ, φ, h] es un punto en coordenadas geodésicas registradas por el receptor GPS; [X, Y , Z] es el punto transformado a coordenadas ECEF (m), siendo [X 0, Y 0, Z 0] el origen definido por el usuario de las coordenadas en ECEF; y [N, E, D] es el punto siendo convertidos en coordenadas LTP (m).
| Punto | Latitud (°) | Latitud (min) | Longitud (°) | Longitud (min) | Altitud (m) |
|---|---|---|---|---|---|
|
Origen |
39 |
28.9761 |
0 |
−20.2647 |
4.2 |
|
1 |
39 |
28.9744 |
0 |
−20.2539 |
5.1 |
|
2 |
39 |
28.9788 |
0 |
−20.2508 |
5.3 |
|
3 |
39 |
28.9827 |
0 |
−20.2475 |
5.9 |
|
4 |
39 |
28.9873 |
0 |
−20.2431 |
5.6 |
|
5 |
39 |
28.9929 |
0 |
−20.2384 |
4.8 |
|
6 |
39 |
28.9973 |
0 |
−20.2450 |
5.0 |
|
7 |
39 |
28.9924 |
0 |
−20.2500 |
5.2 |
|
8 |
39 |
28.9878 |
0 |
−20.2557 |
5.2 |
|
9 |
39 |
28.9832 |
0 |
−20.2593 |
5.4 |
|
10 |
39 |
28.9792 |
0 |
−20.2626 |
5.2 |
|
11 |
39 |
28.9814 |
0 |
−20.2672 |
4.8 |
|
12 |
39 |
28.9856 |
0 |
−20.2638 |
5.5 |
|
13 |
39 |
28.9897 |
0 |
−20.2596 |
5.5 |
|
14 |
39 |
28.9941 |
0 |
−20.2542 |
5.0 |
|
15 |
39 |
28.9993 |
0 |
−20.2491 |
5.0 |
|
16 |
39 |
29.0024 |
0 |
−20.2534 |
5.1 |
|
17 |
39 |
28.9976 |
0 |
−20.2590 |
4.9 |
|
18 |
39 |
28.9929 |
0 |
−20.2643 |
4.9 |
|
19 |
39 |
28.9883 |
0 |
−20.2695 |
4.9 |
|
20 |
39 |
28.9846 |
0 |
−20.2738 |
4.8 |
|
21 |
39 |
28.9819 |
0 |
−20.2770 |
4.7 |
|
22 |
39 |
28.9700 |
0 |
−20.2519 |
4.5 |
MATLAB ® puede proporcionar un entorno de programación conveniente para transformar las coordenadas geodésicas en un marco plano y guardarlas en un archivo de texto. La Tabla 3.4.3 resume los resultados tal y como aparecerían en un archivo MATLAB ® (.m).
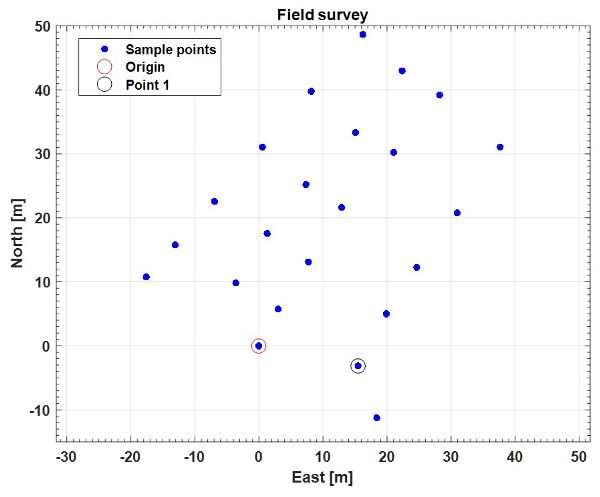
Estos 23 puntos de levantamiento se pueden trazar en un marco cartesiano Este-Norte (es decir, en coordenadas LTP) para ver su distribución espacial en campo, con ejes Oriente y Norte orientados como se muestra en la Figura 3.4.10.
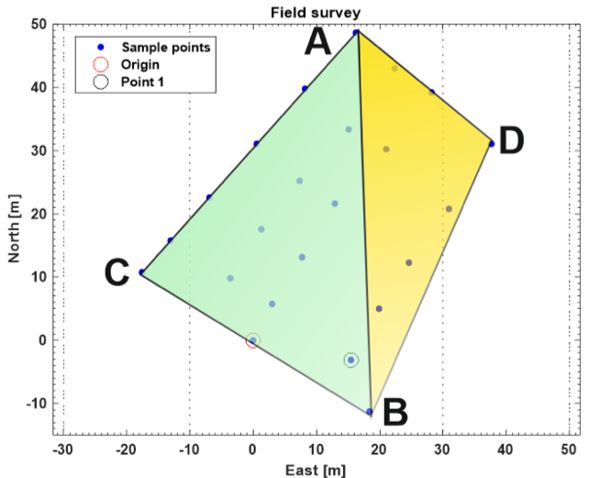
Una ventaja crucial de usar coordenadas planas como LTP es que la geometría euclidiana se puede usar ampliamente para calcular distancias, áreas y volúmenes. Por ejemplo, para calcular el área total cubierta por la rejilla encuestada, divida el trapecio resultante en dos triángulos irregulares (Figura 3.4.11), uno definido por los puntos A-B-C, y el otro por los tres puntos A-B-D. Aplicar geometría euclidiana para calcular el área de un triángulo irregular a partir de la medición de sus tres lados usando la ecuación:
| Punto | Oriente (m) | Norte (m) | Abajo (m) |
|---|---|---|---|
|
Origen |
0 |
0 |
0 |
|
1 |
15.5 |
−3.1 |
−0.9 |
|
2 |
19.9 |
5.0 |
−1.1 |
|
3 |
24.7 |
12.2 |
−1.7 |
|
4 |
31.0 |
20.7 |
−1.4 |
|
5 |
37.7 |
31.1 |
−0.6 |
|
6 |
28.2 |
39.2 |
−0.8 |
|
7 |
21.1 |
30.2 |
−1.0 |
|
8 |
12.9 |
21.6 |
−1.0 |
|
9 |
7.7 |
13.1 |
−1.2 |
|
10 |
3.0 |
5.7 |
−1.0 |
|
11 |
−3.6 |
9.8 |
−0.6 |
|
12 |
1.3 |
17.6 |
−1.3 |
|
13 |
7.3 |
25.2 |
−1.3 |
|
14 |
15.1 |
33.3 |
−0.8 |
|
15 |
22.4 |
42.9 |
−0.8 |
|
16 |
16.2 |
48.7 |
−0.9 |
|
17 |
8.2 |
39.8 |
−0.7 |
|
18 |
0.6 |
31.1 |
−0.7 |
|
19 |
−6.9 |
22.6 |
−0.7 |
|
20 |
−13.0 |
15.7 |
−0.6 |
|
21 |
−17.6 |
10.7 |
−0.5 |
|
22 |
18.3 |
−11.3 |
−0.3 |
\( \text{Area} = \sqrt{K \cdot (K-a) \cdot (K-b)\cdot (K-c)} \)(Ecuación\(\PageIndex{14}\))
donde, a, b, y c son las longitudes de los tres lados del triángulo, y\( K=\frac{a+b+c}{2} \).
La distancia entre dos puntos A y B también se puede determinar mediante la siguiente ecuación:
\( L_{A-B} = \sqrt{(E_{A}-E_{B})^{2} +(N_{A}-N_{B})^{2}} \)(Ecuación\(\PageIndex{15}\))
donde L A-B = distancia euclidiana (línea recta) entre los puntos A y B (m)
[E A, N A] = las coordenadas LTP este y norte del punto A (m)
[E B, N B] = las coordenadas LTP este y norte del punto B (m), calculadas en la Tabla 3.4.3.
Utilizando la ecuación de área, las áreas de los dos triángulos presentados en la Figura 3.4.11 se determinan como 627 m 2 para el triángulo amarillo (ADB) y 1,054 m 2 para el triángulo verde (ABC), con un área total de 1,681 m 2. Las distancias euclidianas correspondientes son 50.9 m, 42.1 m, 60.0 m, 27.8 m y 46.6 m, respectivamente, para L A-C, L C-B, L A-B, L A-D y L D-B, como:
\( L_{A-B} = \sqrt{(E_{A}-E_{B})^{2} +(N_{A}-N_{B})^{2}}=\sqrt{(16.2-18.3)^{2} +(48.7-(-11.3))^{2}} = 60.0 \)
No hemos dicho nada sobre la dirección Z del campo, pero la columna Altitud en la Tabla 3.4.2 y la columna Abajo en la Tabla 3.4.3 ambas sugieren que el campo es bastante plano, ya que la elevación de los puntos sobre el suelo no varía mucho a lo largo de los 22 puntos.
La Figura 3.4.12 muestra los puntos muestreados de la Figura 3.4.10 superpuestos con una imagen satelital que permite a los usuarios conocer detalles adicionales del campo como tipo de cultivo, carriles, edificios circundantes (afectando el rendimiento del GPS) y otra información relevante.
Ejemplo\(\PageIndex{3}\)
Ejemplo 3: Configuración de un sistema de visión artificial para detectar tomates cherry en una cosechadora inteligente
Problema:
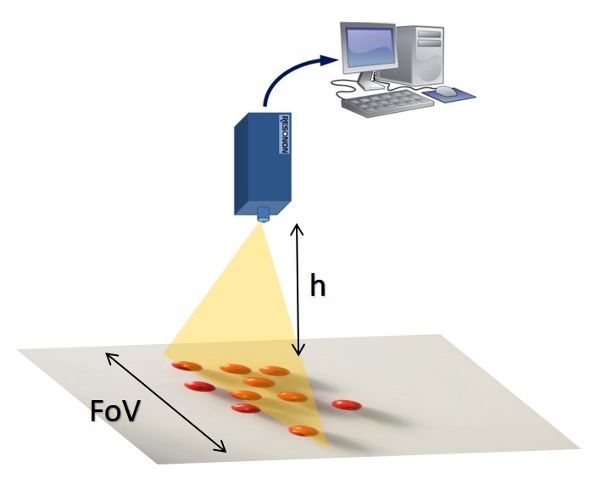
Suponga que está involucrado en el diseño de un sistema de calidad en el campo para la inspección sobre la marcha de productos a bordo de una cosechadora inteligente de tomate cherry. Su asignación específica es el diseño de un sistema de visión artificial para detectar imperfecciones en tomates cherry que son transportados por una cinta transportadora en la cosechadora, como se ilustra en la Figura 3.4.13. Se requiere que utilice una cámara existente que lleve un sensor CCD de dimensiones 6.4 mm × 4.8 mm. El espacio permitido para montar la cámara (altura de la cámara h) está a unos 40 cm por encima del cinturón. Sin embargo, puedes comprar cualquier lente para asegurar un FOV horizontal de 54 cm para cubrir todo el ancho de la cinta transportadora. Determinar la distancia focal requerida de la lente.
Solución
El primer paso en el diseño de este sistema de detección es calcular la distancia focal (f) de la lente necesaria para cubrir el FOV solicitado. Normalmente, el cálculo de la distancia focal requiere conocer dos parámetros principales de la geometría de la lente: la distancia entre el sensor CCD y el centro óptico de la lente, d 1, y la distancia entre el centro óptico de la lente y la cinta transportadora, d 2 . Sabemos que d 2 = 400 mm, FOV = 540 mm, y A, la dimensión horizontal del sensor de imagen, es 6.4 mm, por lo que d 1 se puede determinar fácilmente de acuerdo con las Ecuaciones 3.4.10 y 3.4.11:
\( \frac{d_{1}}{d_{2}} = \frac{A}{FOV} \)(Ecuación\(\PageIndex{11}\))
Por lo tanto,
\( d_{1} = \frac{A \cdot d_{2}}{FOV} = \frac{6.4 \cdot 400}{540} = 4.74 \ mm \)
La distancia focal, f, se puede determinar usando la Ecuación 3.4.10:
\( \frac{1}{f} = \frac{1}{d_{1}} + \frac{1}{d_{2}} \)(Ecuación\(\PageIndex{10}\))
Por lo tanto,
\( f= \frac{d_{1} \cdot d_{2}}{d_{1} + d_{2}} = \frac{4.74 \cdot 400}{4.74 + 400} = 4.68 \ mm \)
Ningún fabricante de lentes probablemente ofrecerá una lente con una distancia focal de 4.68 mm; por lo tanto, debe elegir el más cercano de lo que está disponible comercialmente. Las lentes disponibles comercialmente para esta cámara tienen las siguientes distancias focales: 2.8 mm, 4 mm, 6 mm, 8 mm, 12 mm y 16 mm. Un enfoque adecuado es elegir el mejor lente para esta aplicación, y reajustar la distancia entre la cámara y el cinturón para mantener cubierto el FOV solicitado. Fuera de la lista ofrecida anteriormente, la mejor opción es elegir una lente con f = 4 mm. Esa elección cambiará ligeramente los parámetros originales, y tendrás que reajustar algunas de las condiciones iniciales para mantener el mismo FOV, que es la condición principal a cumplir. La modificación más fácil será bajar la posición de la cámara a una distancia de 34 cm al transportador (d 2 = 340 mm de la ecuación de distancia focal). Si la cámara es fija y d 2 tiene que permanecer en los 40 cm iniciales, el campo de visión resultante sería mayor que los 54 cm necesarios, y sería necesario aplicar técnicas de procesamiento de imágenes para eliminar secciones inútiles de las imágenes.
Ejemplo\(\PageIndex{4}\)
Ejemplo 4: Estimación de la velocidad de un robot usando un acelerómetro
Problema:
| Punto de datos | Tiempo (s) | Aceleración (g) |
|---|---|---|
|
1 |
7.088 |
0.005 |
|
2 |
8.025 |
0.018 |
|
3 |
9.025 |
0.009 |
|
4 |
10.025 |
0.009 |
|
5 |
11.025 |
0.008 |
|
6 |
12.025 |
0.009 |
|
7 |
13.025 |
0.009 |
|
8 |
14.025 |
0.009 |
|
9 |
15.025 |
0.008 |
|
10 |
16.025 |
0.008 |
|
11 |
17.025 |
0.009 |
|
12 |
18.025 |
0.009 |
|
13 |
19.025 |
0.008 |
|
14 |
20.088 |
0.009 |
|
15 |
21.088 |
−0.009 |
|
16 |
21.963 |
−0.019 |
|
17 |
23.025 |
−0.001 |
El acelerómetro de la Figura 3.4.14a se instaló en el robot agrícola de la Figura 3.4.14c. Al desplazarse por hileras de viñedos, las mediciones de salida del acelerómetro se registraron en la Tabla 3.4.4, incluyendo el tiempo de cada medición y su correspondiente aceleración lineal en la dirección hacia adelante dada en g, la aceleración gravitacional.
- 1. Calcular la aceleración instantánea de cada punto en m·s −2, tomando en cuenta que un g equivale a 9.8 m·s −2.
- 2. Calcular el tiempo transcurrido entre mediciones consecutivas Δ t en s.
- 3. Estimar la frecuencia de muestreo promedio (Hz) a la que estaba funcionando el acelerómetro.
- 4. Calcular la velocidad correspondiente para cada medición con la Ecuación 3.4.12, tomando en cuenta que el vehículo arrancó desde una posición de reposo (V 0 = 0 m s −1) y siempre se movió hacia adelante.
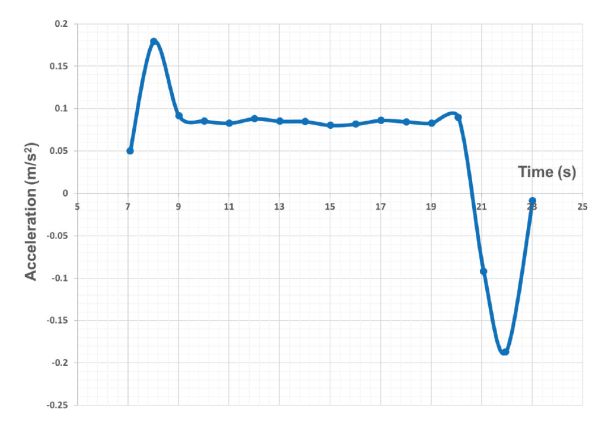
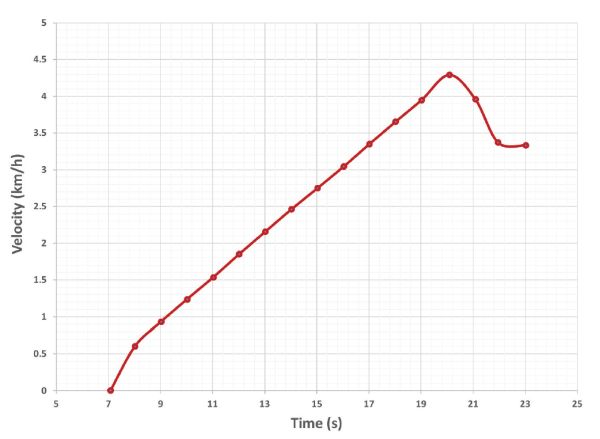
- 5. Trazar la aceleración del robot (m s −2) y la velocidad (km h −1) durante la duración de la prueba.
(a)
b)
c)
Figura\(\PageIndex{14}\): (a) Acelerómetro Gulf Coast X2-2; (b) montaje del sensor; (c) en un robot agrícola.
Solución
| Punto de datos | Tiempo (s) | Aceleración (g) | Aceleración (m s −2) | ∆t (s) |
|---|---|---|---|---|
|
1 |
7.088 |
0.005 |
0.050 |
0 |
|
2 |
8.025 |
0.018 |
0.179 |
0.938 |
|
3 |
9.025 |
0.009 |
0.091 |
1.000 |
|
4 |
10.025 |
0.009 |
0.085 |
1.000 |
|
5 |
11.025 |
0.008 |
0.083 |
1.000 |
|
6 |
12.025 |
0.009 |
0.088 |
1.000 |
|
7 |
13.025 |
0.009 |
0.085 |
1.000 |
|
8 |
14.025 |
0.009 |
0.084 |
1.000 |
|
9 |
15.025 |
0.008 |
0.080 |
1.000 |
|
10 |
16.025 |
0.008 |
0.081 |
1.000 |
|
11 |
17.025 |
0.009 |
0.086 |
1.000 |
|
12 |
18.025 |
0.009 |
0.084 |
1.000 |
|
13 |
19.025 |
0.008 |
0.083 |
1.000 |
|
14 |
20.088 |
0.009 |
0.089 |
1.063 |
|
15 |
21.088 |
−0.009 |
−0.092 |
1.000 |
|
16 |
21.963 |
−0.019 |
−0.187 |
0.875 |
|
17 |
23.025 |
−0.001 |
−0.009 |
1.063 |
|
Promedio |
0.996 |
|||
De acuerdo con los resultados anteriores, el tiempo promedio transcurrido entre dos mediciones consecutivas ∆t es de 0.996 s, lo que corresponde aproximadamente a una medición por segundo, o 1 Hz. La velocidad de un vehículo se puede estimar a partir de su aceleración con la Ecuación 3.4.12. En el Cuadro 3.4.5 se especifica el cálculo en cada medición específica.
La Figura 3.4.15 representa la aceleración medida y la velocidad calculada para un intervalo de tiempo dado de 16 segundos. Observe que hay puntos de datos con una aceleración negativa (desaceleración) pero la velocidad nunca es negativa porque el vehículo siempre se movió hacia adelante o se mantuvo en reposo. Los acelerómetros sufren estimaciones ruidosas, y como resultado, la velocidad final calculada en la Tabla 3.4.5 puede no ser muy precisa. En consecuencia, es una buena práctica estimar las velocidades de los vehículos de manera redundante con al menos dos sensores independientes que funcionen bajo diferentes principios. En este ejemplo, por ejemplo, también se estimó la velocidad de avance con un receptor GPS a bordo.
| Punto de datos | Aceleración (m s −2) | ∆t (s) | Velocidad (m s −1) | V (km h −1) |
|---|---|---|---|---|
|
1 |
0.050 |
0 |
V 1 = V 0 + a 1 · ∆t = 0 + 0.05 · 0 = 0 |
0.0 |
|
2 |
0.179 |
0.938 |
V 2 = V 1 + a 2 · ∆t = 0 + 0.179 · 0.938 = 0.17 |
0.6 |
|
3 |
0.091 |
1.000 |
V 3 = V 2 + a 3 · ∆t = 0.17 + 0.091 · 1 = 0.26 |
0.9 |
|
4 |
0.085 |
1.000 |
0.34 |
1.2 |
|
5 |
0.083 |
1.000 |
0.43 |
1.5 |
|
6 |
0.088 |
1.000 |
0.51 |
1.9 |
|
7 |
0.085 |
1.000 |
0.60 |
2.2 |
|
8 |
0.084 |
1.000 |
0.68 |
2.5 |
|
9 |
0.080 |
1.000 |
0.76 |
2.7 |
|
10 |
0.081 |
1.000 |
0.84 |
3.0 |
|
11 |
0.086 |
1.000 |
0.93 |
3.3 |
|
12 |
0.084 |
1.000 |
1.01 |
3.7 |
|
13 |
0.083 |
1.000 |
1.10 |
3.9 |
|
14 |
0.089 |
1.063 |
1.19 |
4.3 |
|
15 |
-0.092 |
1.000 |
1.10 |
4.0 |
|
16 |
-0.187 |
0.875 |
0.94 |
3.4 |
|
17 |
-0.009 |
1.063 |
0.93 |
3.3 |
Créditos de imagen
Figura 1a. John Deere. (2020). Segadora autónoma. Recuperado de www.deere.es/es/campaigns/ag-turf/tango/. [Uso justo].
Figura 1b. Rovira-Más, F. (CC BY 4.0). (2020). b) Transplantadora autónoma de arroz basada en GPS.
Figura 2. Investigación de Mercado Verificada (2018). (CC POR 4.0). (2020). Crecimiento esperado del mercado de robots agrícolas.
Figura 3. Rovira-Más, F. (CC BY 4.0). (2020). Arquitectura de sensores para vehículos agrícolas inteligentes.
Figura 4. Rovira-Más, F. (CC BY 4.0). (2020). Relación geométrica entre un sensor de imagen, lente y FOV.
Figura 5. Rovira-Más, F. (CC BY 4.0). (2020). Segmentación a base de color de mandarinas.
Figura 6. Rovira-Más, F. (CC BY 4.0). (2020). Sistemas de guía automática: (a) Kit de barra de luz; (b) Pantalla de control de seguimiento paralelo.
Figura 7. Zhang, Q. (CC BY 4.0). (2020). Sistemas de dirección de tractores: (a) sistema de dirección hidráulica tradicional; y (b) sistema de dirección electrohidráulico.
Figura 8. Adaptado de T. Karvinen, K. Karvinen, V. Valtokari (Make: Sensors, Maker Media, 2014). (2020). Montaje de un telémetro ultrasónico HC-SR04 con un procesador Arduino. [Uso justo].
Figura 9. Rovira-Más, F. (CC BY 4.0). (2020). Digitalización de una señal analógica con 4 bits entre 1.2 V y 4.7 V.
Figura 10. Rovira-Más, F. (CC BY 4.0). (2020). Representación plana de los 23 puntos muestreados en el campo con origen local.
Figura 11. Rovira-Más, F. (CC BY 4.0). (2020). Estimación del área cubierta por los puntos muestreados en el campo encuestado.
Figura 12. Saiz-Rubio, V. (CC BY 4.0). (2020). Puntos muestreados sobre una imagen satelital de la parcela encuestada (origen en el número 23).
Figura 13. Rovira-Más, F. (CC BY 4.0). (2020). Requisitos geométricos de un sistema de inspección basado en visión para una cinta transportadora en una cosechadora.
Figura 14a. Conceptos de datos de la costa del Golfo. (2020). Acelerómetro Costa del Golfo X2-2. Recuperado de http://www.gcdataconcepts.com/x2-1.html. [Uso justo].
Figura 14b y 14c. Saiz-Rubio, V. (CC BY 4.0). (2020). (b) montaje del sensor. (c) montar un robot agrícola.
Figura 15. Rovira-Más, F. (CC BY 4.0). (2020). Aceleración y velocidad de un robot de granja estimada con un acelerómetro.
Referencias
Bolton, W. (1999). Mecatrónica (2ª ed). Nueva York: Addison Wesley Longman Publishing.
Myklevy, M., Doherty, P., & Makower, J. (2016). La nueva gran estrategia. Nueva York: St. Martin's Press.
Rovira-Más, F., Zhang, Q., & Hansen, A. C. (2010). Mecatrónica y sistemas inteligentes para vehículos todoterreno. Londres: Springer-Verlag.
Russell, S., & Norvig, P. (2003). Inteligencia artificial: un enfoque moderno (2a ed.). Upper Saddle River, NJ: Prentice Hall.
Investigación de Mercado Verificada. (2018). Los robots agrícolas globales comercializan tamaño por tipo (tractores sin conductor, máquina cosechadora automatizada, otros), por aplicación (cultivo de campo, manejo de lácteos, agricultura de interior, otros), por alcance geográfico y pronóstico. ID del reporte: 3426. Verified Market Research Inc.: Boonton, NJ, EUA, pp. 78.