5.2: Diseño de Edificios para Viviendas Ganaderas Eficientes Energéticamente
- Page ID
- 80881
Andrea Costantino
Grupo de Investigación TEBE
Departamento de Energía
Politecnico di Torino
Torino, Italia
y
Instituto de Ciencia y Tecnología Animal
Universitat Politècnica de València
València, España
Enrico Fabrizio
Grupo de Investigación TEBE
Departamento de Energía
Politecnico di Torino
Torino, Italia
| Términos Clave |
| Balance energético | Calefacción suplementaria | Climatización |
| Balance de masa | Recuperación de calor | Ventilación |
| Gestión energética | Sistemas de refrigeración |
Variables
Introducción
El uso de energía en las granjas se considera directo cuando se usa para operar maquinaria y sistemas de climatización o indirecto cuando se usa para fabricar piensos y agroquímicos. El consumo directo de energía en la granja se estimó en 6 EJ año −1, lo que representa alrededor de 1.2% del consumo total de energía mundial (OCDE, 2008). Si se incluye la energía indirecta, el consumo total de energía agrícola podría ser de hasta 15 EJ año −1, lo que representa alrededor de 3.1% del consumo global de energía. La ganadería alojada requiere condiciones de clima interior adecuadas para maximizar tanto la producción como el bienestar, especialmente evitando el estrés térmico. La tarea del ingeniero es mejorar la eficiencia de uso energético de las viviendas ganaderas y minimizar el consumo de energía. Esto se puede lograr mejorando el rendimiento energético de los equipos utilizados para el control climático y el diseño del edificio.
El enfoque de este capítulo es el diseño de edificios para el manejo eficiente de la energía en las viviendas ganaderas. Mejorar el diseño de edificios requiere comprender el balance de masa y energía del sistema para especificar los materiales, dimensiones y equipos necesarios para mantener condiciones de operación seguras. La importancia de entender las necesidades energéticas de los edificios queda ilustrada por el reporte de St-Pierre et al. (2003), quienes estimaron las pérdidas económicas por parte de la industria láctea en Estados Unidos en $1.69 a $2.36 mil millones anuales debido al estrés térmico. Comprender y ser capaz de usar conceptos fundamentales para el diseño de viviendas de animales proporciona la base para un bienestar deseable y una vivienda animal más eficiente centrada en la producción.
Resultados
Después de leer este capítulo, deberías poder:
- • Describir las necesidades energéticas para la vivienda ganadera
- • Explicar los requerimientos de manejo energético de una casa ganadera
- • Describir los principales sistemas de climatización utilizados para la vivienda ganadera y las características que afectan la gestión energética
- • Calcular balances energéticos para casas ganaderas
Conceptos
Balance Energético y Masico de una Casa Ganadera
Termodinámicamente, una casa ganadera es un sistema abierto que intercambia energía y masa (como aire, humedad y contaminantes) entre los ambientes interiores y exteriores y los animales que ocupan el volumen interno (el recinto). La ley de conservación de energía y masa es el principio básico para el balance de masas. Las paredes, el piso y el techo del edificio representan las superficies de control y encierran el volumen de control del sistema termodinámico representado por la casa de ganado y sus superficies internas, como animales, paredes interiores y equipos. Las ecuaciones de energía y balance de masa permiten el análisis del comportamiento térmico de una casa ganadera, pero calcular estos balances es un desafío porque muchos factores afectan el comportamiento térmico de estos edificios. Es fundamental entender qué términos considerar, y qué asumir como despreciables.
Balance Energético
El calor sensible es la cantidad de calor intercambiado por un cuerpo y el sistema termodinámico circundante que implica un cambio de temperatura. El calor latente es el calor absorbido o liberado por una sustancia durante un cambio de fase sin cambio de temperatura. Estas dos formas de calor se pueden ilustrar usando un ejemplo de calentamiento de una olla de agua en una estufa. Inicialmente, el agua está a temperatura ambiente (digamos, 25°C), y a medida que el agua se calienta, su temperatura aumenta. El calor que provoca el aumento de temperatura es calor sensible y para el agua es igual a 4,186 kJ kg −1 K −1. Cuando la temperatura del agua alcanza los 100°C (punto de ebullición del agua a presión atmosférica), el agua cambia de fase de líquido a gas (vapor). El calor proporcionado durante el cambio de fase rompe los enlaces moleculares del agua líquida para hacer la transición a la fase gaseosa, pero la temperatura no cambia. El calor suministrado para efectuar el cambio de fase es calor latente. El calor latente de vaporización para una unidad de masa de agua es de 2,272 kJ kg −1 a 100°C y presión atmosférica.
El balance energético de una casa ganadera, considerando solo el calor sensible, puede escribirse de la siguiente manera (Panagakis y Axaopoulos, 2008):
\[ \phi_{a}+\phi_{tr}+\phi_{sol}+\phi_{f}+\phi_{v}+\phi_{m}+(\gamma_{fog}\cdot \phi_{H})=\sum^{n}_{k=1}(M_{el,k}\cdot C_{el,k})\cdot \frac{dT_{air,i}}{dt} \]
donde\(\phi_{a}\) = flujo de calor sensible de los animales dentro del recinto (W)
\(\phi_{tr}\)= flujo de calor sensible debido a la transmisión a través de las superficies de control pero excluyendo el piso (W)
\(\phi_{sol}\)= flujo de calor sensible debido a la radiación solar a través de elementos de construcción opacos y acristalados (W)
\(\phi_{f}\)= flujo de calor sensible debido a la transmisión a través del piso (W)
\(\phi_{v}\)= flujo de calor sensible debido a la ventilación (W)
\(\phi_{m}\)= flujo de calor sensible de fuentes internas, como motores y luces (W)
\(\gamma_{fog}\)= Variable booleana para la presencia (\(\gamma_{fog}\)=1) o no (\(\gamma_{fog}\)=0) de un sistema de nebulización dentro de la casa de ganado
\(\phi_{fog}\)= flujo de calor sensible debido al sistema de empañamiento (W)
\(\gamma_{H}\)= Variable booleana para la presencia (\(\gamma_{H}\)=1) o no (\(\gamma_{H}\)=0) de un sistema de calefacción suplementario dentro de la casa de ganado
\(\phi_{H}\)= flujo de calor sensible debido al sistema de calefacción suplementario (W)
\(M_{el,k}\)= masa del k-ésimo elemento de construcción (kg)
\(C_{el,k}\)= capacidad calorífica total del k-ésimo elemento de construcción (kJ kg −1 K −1)
\(\frac{dT_{air,i}}{dt}\)= variación de la temperatura del aire interior\(T_{air,i}\) con el tiempo t
Al usar la Ecuación 5.2.1 para cálculos y dimensionamiento, preste atención a los flujos de calor porque cada término podría ser positivo o negativo dependiendo del contexto físico. Por lo general, los flujos de calor que entran en un volumen de control (la casa de animales) son positivos, y los que salen son negativos. Por ejemplo, en la Ecuación (5.2.1), los términos\(\phi_{a}\) y\(\phi_{sol}\) son siempre positivos o cero, ya que representan el flujo de calor entrante de los animales y la radiación solar, respectivamente, mientras que los valores de\(\phi_{tr}\) y\(\phi_{v}\) podrían ser positivos o negativos, dependiendo de la diferencia de temperatura dentro y fuera de la casa de animales. El término\(\phi_{f}\) depende de la construcción del piso. Aunque\(\phi_{tr}\) y\(\phi_{f}\) son ambos flujos de calor de transmisión a través de la superficie de control, siempre están separados. Estimar la transferencia de calor a través del suelo es muy desafiante (Albright, 1990; Panagakis y Axaopoulos, 2008; Costantino et al., 2017), por ejemplo, en casas de cerdos con fosas ventiladas para almacenamiento de estiércol. Para simplificar el balance energético, el término\(\phi_{tr}\) suele considerarse como la suma de\(\phi_{tr}\) y\(\phi_{f}\) y se utiliza un coeficiente correctivo cuando\(\phi_{f}\) se calcula.
El término siempre\(\phi_{fog}\) es negativo porque representa el calor sensible que eliminan las gotas de agua de un sistema de nebulización. Un sistema de nebulización proporciona enfriamiento dentro de la casa de los animales al poner una neblina de pequeñas gotas de agua en el aire para proporcionar enfriamiento evaporativo para los animales. El término siempre\(\phi_{H}\) es positivo. Los parámetros\(\gamma_{fog}\) y no\(\gamma_{H}\) deben tener un valor de 1 al mismo tiempo sino que ambos pueden ser 0.
El calor sensible de los animales,\(\phi_{a}\), depende de la especie y la masa corporal y la temperatura ambiente. Los valores de calor sensible y latente se pueden encontrar en la literatura, por ejemplo de ASABE (2012), Hellickson & Walker (1983), o Lindley & Whitaker (1996), y datos más detallados están disponibles en Pedersen y Sällvik (2002), quienes expresan calor sensible y latente de los animales en función del peso del animal, temperatura del aire interior y actividad animal. En las casas de animales complejos se puede incluir el flujo de calor sensible de fuentes internas, como motores (ventiladores y sistemas de alimentación automática\(\phi_{m}\)) y término de luces () (Albright, 1990), pero en muchos cálculos se excluye porque es muy pequeño en comparación con\(\phi_{a}\) (Midwest Plan Service, 1987). Esa exclusión se justifica aún más cuando se utilizan tecnologías de bajo consumo como lámparas de LED/descarga de gas y motores sin escobillas.
El producto\(M_{el}\cdot C_{el}\) es la capacidad calorífica efectiva agrupada de un elemento de construcción expresado en kJ K −1. Para cada elemento de construcción (paredes y techo) se debe conocer la cantidad o masa de material, y la cantidad de energía térmica necesaria para elevar la temperatura de una unidad de masa del material en un grado centígrados. La fracción\(\frac{dT_{air,i}}{dt}\) representa la variación de la temperatura del aire interior a través del tiempo. Este lado de la ecuación representa el cambio de temperatura del propio edificio.
Es posible incluir términos adicionales a la Ecuación 5.2.1 (Albright, 1990; Esmay y Dixon, 1986) como el flujo de calor sensible para evaporar el agua dentro del volumen de control desde estructuras como canales de agua y un almacén de lodo (\(\phi_{e}\)). Algunos autores lo consideran importante (Hamilton et al., 2016), mientras que otros no (Midwest Plan Service, 1987). Liberati y Zappavigna (2005) consideran que el intercambio de calor sensible entre el estiércol (especialmente cuando se recolecta en fosas) y el aire dentro del recinto (\(\phi_{man}\)) es importante en casas a gran escala equipadas con pozos de almacenamiento y estiércol cuando no se retira con frecuencia. Una variable booleana\(\gamma_{man}\) puede generalizar aún más la Ecuación 5.2.1.
La ecuación 5.2.1 es un balance energético dinámico. Si se asume un paso de tiempo grande (quizás una semana o más), se puede escribir para condiciones de estado estacionario, lo que significa que las variables de estado que describen el sistema pueden considerarse constantes con el tiempo, y los términos del saldo representan los valores promedio para el sistema. Para grandes pasos de tiempo o en condiciones de estado estacionario con temperatura constante del aire interior y exterior, la acumulación de calor por el propio edificio puede considerarse cero, por lo que la Ecuación 5.2.1 se convierte en:
\[ \phi_{a}+\phi_{tr}+\phi_{sol}+\phi_{v}+\gamma_{fog}\cdot \phi_{fog}=0 \]
Para obtener el balance energético de una caseta ganadera en estado frío que requiera calefacción suplementaria, el balance energético se convierte en:
\[ \phi_{a}+\phi_{tr}+\phi_{H}+\phi_{sol}+\phi_{v}=0 \]
La Figura 5.2.1 presenta una ilustración del balance de calor sensible de la Ecuación 5.2.3 para viviendas simples de vacas lecheras. La Ecuación 5.2.3 puede ser utilizada para diseñar una casa ganadera básica. Sin duda, la formulación presentada es una simplificación, y en la literatura, se introducen otros términos en el balance energético. El cálculo de cada término del balance energético de la Ecuación 5.2.3 se proporciona con mayor detalle más adelante en este capítulo.
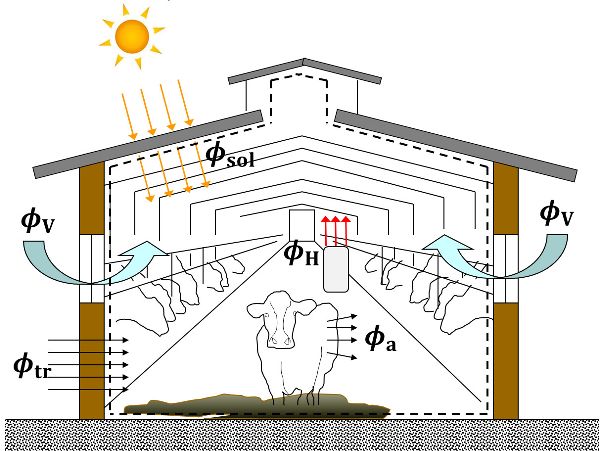
Balance de Masa
Los balances de masas son necesarios para planificar el manejo de contaminantes, tales como dióxido de carbono (CO 2), sulfuro de hidrógeno (H 2 S) y amoníaco (NH 3), producidos por los animales (Esmay y Dixon, 1986) y para regular la temperatura ambiente interior, el contenido de humedad, y humedad. Junto con la temperatura y humedad relativa, la calidad del aire interior (IAQ) debe ser controlada por ventilación para evitar problemas de salud animal. El cálculo de los requisitos de ventilación para el control de contaminantes es un problema de balance de masas Con bajas temperaturas del aire interior, se utiliza un caudal mínimo de ventilación (ventilación base) para diluir contaminantes como H 2 S y NH 3. Se puede aumentar el caudal mínimo de ventilación para reducir el contenido de humedad. Cuando la temperatura del aire interior es superior a la temperatura del punto de ajuste de enfriamiento utilizada para mantener la comodidad de los animales, se debe aumentar el caudal de ventilación para enfriar a los animales (Esmay y Dixon, 1986). El caudal máximo de ventilación debe evitar altas velocidades de aire que perjudiquen el bienestar animal. Si no se puede lograr el enfriamiento usando flujo másico, se puede usar un sistema de nebulización. El flujo de aire de ventilación se puede expresar en m 3 s −1, m 3 h −1 o como ach (cambios de aire por hora), lo que indica cuántas veces se cambia el volumen de aire dentro de la casa en una hora.
Para estimar el caudal de ventilación para el control de humedad en una casa de ganado simple, se puede utilizar la Ecuación 5.2.4 (Panagakis y Axaopoulos, 2008):
\[ \dot{V}_{air}\cdot \rho_{air}\cdot(x_{air,i}-x_{air,o})+\dot{m}_{a}+(\gamma_{fog} \cdot \dot{m}_{fog})=\rho_{air,i} \cdot V_{air,i} \cdot \frac{dx_{air,i}}{dt} \]
donde\(\dot{V}_{air}\) = caudal de aire de ventilación (m 3 s −1)
\(\rho_{air}\)= densidad de masa volumétrica (kg m 3)
\(x_{air,o}\)= humedad específica del aire exterior (kg vapor kg aire −1)
\(x_{air,i}\)= humedad específica del aire interior (kg vapor kg aire −1)
\(\dot{m}_{a}\)= producción de vapor de agua animal (kg de vapor s −1)
\(\gamma_{fog}\)= Variable booleana que indica la presencia de sistema de nebulización
\(\dot{m}_{fog}\)= agua añadida a través del empañamiento (kg de vapor s −1)
\(\rho_{air,i}\)= densidad de masa volumétrica del aire interior (kg m −3)
\(V_{air,i}\)= volumen del aire interior (m 3)
\(\frac{dx_{air,i}}{dt}\)= variación\(x_{air,i}\) del tiempo t
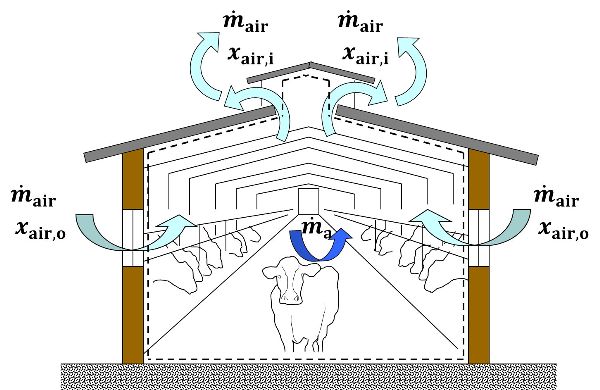
En condiciones de estado estacionario y sin considerar la presencia de sistemas de nebulización, el balance de masas (Figura 5.2.2) puede simplificarse como:
\[ \dot{m}_{air} \cdot x_{air,i} - \dot{m}_{air} \cdot x_{air,i} + \dot{m}_{a} = 0 \]
La ecuación 5.2.5 es la formulación básica del balance de masa de humedad en condiciones de estado estacionario para las casas ganaderas.
Cálculos de Gestión Energética
Las bases para los cálculos de energía sensible y balance de masas para la vivienda ganadera son las Ecuaciones 5.2.3 y 5.2.5, respectivamente. En los siguientes apartados se presenta la determinación de cada término del balance energético (Ecuación 5.2.3). Se podría utilizar un enfoque similar para la Ecuación 5.2.5.
Flujo de calor de los animales criados (\(\phi_{a}\))
Los animales producen y contribuyen considerablemente al flujo de calor en su vivienda. En condiciones frías, este flujo de calor puede ayudar a calentar el edificio y disminuir la necesidad de calor suplementario. En condiciones cálidas, este flujo de calor debe eliminarse para evitar el sobrecalentamiento y causar estrés por calor animal. Los animales necesitan emitir calor (tanto calor sensible como latente) para regular su temperatura corporal y mantener sus funciones corporales. A medida que un animal crece (generalmente el resultado deseado de un sistema de producción de carne, pero no para lecheros y gallinas ponedoras), el animal produce más calor. La cantidad de calor también depende de la temperatura del aire interior, los objetivos de producción (como la masa de huevos, leche o carne) y la concentración de energía del pienso. Estimar la producción de calor también es esencial para calcular los requisitos de ventilación.
Los valores estándar para la producción de calor están disponibles (CIGR, 1999; ASABE, 2012), pero es posible un cálculo específico (Pedersen y Sällvik, 2002). Primero se calcula el calor total producido,\(\phi_{a,tot}\) (suma del calor sensible y latente), para la casa de animales para una temperatura del aire interior de 20°C La formulación de la ecuación depende de la especie animal y la producción:
Pollos de engorde:\[ \phi_{a,tot} =10.62\cdot w_{a}^{0.75} \cdot n_{a} \]
Gallinas ponedoras:\[\phi_{a,tot} =(6.28\cdot w_{a}^{0.75} + 25\cdot Y_{eggs}) \cdot n_{a} \]
Cerdos de engorde:\[ \phi_{a,tot} =(5.09 \cdot +[1-(0.47+0.003 \cdot w_{a})] \cdot [5.09 \cdot w_{a}^{0.75} \cdot (Y_{feed}-1)]) \cdot n_{a} \]
Vacas lecheras:\[ \phi_{a,tot} =(5.6\cdot w_{a}^{0.75} + 22\cdot Y_{milk} +1.6\cdot 10^{-5}\cdot Y_{pregnancy}^{3} )\cdot n_{a} \]
donde\(w_{a}\) = peso vivo promedio del animal (kg)
\(n_{a}\)= número de animales dentro de la casa de ganado (animales)
\(Y_{eggs}\)= producción de huevos (kg día −1), generalmente entre 0.04 (producción de cría) y 0.05 kg día −1 (huevos de consumo)
\(Y_{feed}\)= coeficiente adimensional relacionado con la ingesta diaria de energía alimentaria por los cerdos (los valores de\(Y_{feed}\) se presentan en la Tabla 5.2.1)
\(Y_{milk}\)= producción de leche (kg día −1)
\(Y_{pregnancy}\)= número de días de embarazo (días)
A continuación, se calcula el calor sensible producido (\(\phi_{a}\)) a una temperatura dada del aire interior. Si la temperatura del aire interior está en la zona termoneutral, es decir, un rango de temperatura donde la disipación de calor animal es constante (Pedersen y Sällvik, 2002) y la fracción de energía utilizada por los animales para mantener su homeotermia es mínima, a nivel de casa se\(\phi_{a}\) puede calcular como:
| Masa Corporal de Cerdo (kg) |
Alimentación Y | ||
|---|---|---|---|
| Tasa de Ganancia: 700 g día −1 | Tasa de ganancia: 800 g día −1 | Tasa de ganancia: 900 g día −1 | |
|
20 |
3.03 |
3.39 |
3.39 |
|
30 |
2.79 |
3.25 |
3.25 |
|
40 |
2.60 |
3.22 |
3.43 |
|
50 |
2.73 |
3.16 |
3.41 |
|
60 |
2.78 |
3.16 |
3.40 |
|
70 |
2.84 |
3.12 |
3.40 |
|
80 |
2.83 |
3.04 |
3.38 |
|
90 |
2.74 |
2.79 |
3.18 |
|
100 |
2.64 |
2.57 |
2.98 |
|
110 |
2.52 |
2.40 |
2.78 |
|
120 |
2.36 |
2.25 |
2.60 |
Casa de pollos de engorde:\[ \phi_{a}=\{0.61 \cdot[1000+20 \cdot (20-T_{air,i})]-0.228 \cdot T_{air,i}^{2} \} \cdot n_{hpu} \]
Gallinero ponedora:\[ \phi_{a}=\{0.67 \cdot[1000+20 \cdot (20-T_{air,i})]-9.8\cdot 10^{-8} \cdot T_{air,i}^{6} \} \cdot n_{hpu} \]
Casa de cerdo de engorde:\[ \phi_{a}=\{0.62 \cdot[1000+12 \cdot (20-T_{air,i})]-1.15\cdot 10^{-7} \cdot T_{air,i}^{6} \} \cdot n_{hpu} \]
Casa de vaca lechera:\[ \phi_{a}=\{0.71 \cdot[1000+4 \cdot (20-T_{air,i})]-0.408 \cdot T_{air,i}^{2} \} \cdot n_{hpu} \]
donde\(T_{air,i}\) = temperatura del aire interior (°C)
\(n_{hpu}\)= el número de unidades productoras de calor (hpu) que están presentes dentro de la casa de ganado
Un hpu se define como el número de animales que produce 1000 W de calor total (suma de calor sensible y latente) a una temperatura del aire interior de 20°C y puede calcularse como:
\[ n_{hpu} = \frac{\phi_{a,tot}}{1000} \]
donde\(\phi_{a,tot}\) se calcula utilizando las Ecuaciones 5.2.6, 5.2.7, 5.2.8 o 5.2.9 dependiendo de la especie y sistema de producción. Fuera de la zona termoneutral, no se puede encontrar una relación clara entre la temperatura del aire interior y la producción total de calor, pero los valores se pueden calcular utilizando las formulaciones presentes en Pedersen y Sällvik (2002).
Flujo de calor de transmisión a través de la envolvente del edificio (\(\phi_{tr}\))
El término\(\phi_{t}\) se está tomando para representar el flujo de calor a través de las paredes, techo, ventanas, puertas y piso. Se calcula como (Comité Europeo de Normalización, 2007):
\[ \phi_{tr}=[\sum^{n}_{j=1}(b_{tr,j} \cdot U_{j} \cdot A_{j})] \cdot (T_{air,o}-T_{air,i}) \]
donde b tr = factor de corrección adimensional entre 0 y 1
\(U_{j}\)= transmitancia térmica del elemento de construcción j (W m −2 K −1)
\(A_{j}\)= área total del elemento de construcción j (m 2)
\(T_{air,o}\)= temperatura del aire exterior (°C)
El factor\(b_{tr}\) se utiliza para corregir el flujo de calor cuando la diferencia de temperatura forzada no es la diferencia entre el aire interior y exterior, por ejemplo cuando el flujo de calor ocurre hacia espacios no acondicionados (por ejemplo, almacenes de material y salas de control de clima) o a través del suelo. En estos casos, se puede utilizar la diferencia de temperatura del aire entre el interior y el exterior pero el flujo de calor disminuye usando\(b_{tr}\). Este coeficiente puede calcularse en dos casos: (1) si la temperatura del espacio adyacente es fija y conocida, o (2) si todos los coeficientes de transferencia de calor entre los espacios considerados pueden estimarse numéricamente. En la mayoría de las situaciones,\(b_{tr}\) (sin unidades) se obtiene a partir de estándares, (por ejemplo, Cuadro 5.2.2).
| Tipo de Espacio No Acondicionado | b tr |
|---|---|
|
Espacio con 1 revestimiento de pared en el ambiente exterior |
0.40 |
|
Espacio con 2 paredes orientadas al ambiente exterior (sin puertas) |
0.50 |
|
Espacio con 2 paredes orientadas al ambiente exterior (con puertas) |
0.60 |
|
Espacio con 3 paredes orientadas al ambiente exterior (con puertas) |
0.80 |
|
Piso en contacto directo con el suelo |
0.45 |
|
Piso ventilado (por ejemplo, fosas y cavidad debajo del piso) |
0.80 |
Flujo de calor debido a un sistema de calefacción suplementario (\(\phi_{H}\))
En la mayoría de los casos,\(\phi_{H}\) es lo desconocido del problema y el balance energético se resuelve con el objetivo de encontrar su valor. Un ejemplo típico es resolver el balance energético de la Ecuación 5.2.3 para encontrar\(\phi_{H}\) y dimensionar la capacidad de calentamiento del sistema de calefacción suplementario. En otros casos,\(\phi_{H}\) podría ser igual a cero y lo desconocido del problema podría ser![]() con el objetivo de encontrar el caudal de ventilación necesario para mantener cierta temperatura del aire interior y enfriar a los animales criados. Rara vez,\(\phi_{H}\) tiene que ser estimado. Por ejemplo, se\(\phi_{H}\) tiene que estimar cuando se resuelve el balance energético con el objetivo de evaluar la temperatura del aire interior en condiciones de límite específicas dadas. Una manera fácil de estimar\(\phi_{H}\) es considerar la capacidad de calentamiento reportada en la ficha técnica del equipo para calefacción suplementaria.
con el objetivo de encontrar el caudal de ventilación necesario para mantener cierta temperatura del aire interior y enfriar a los animales criados. Rara vez,\(\phi_{H}\) tiene que ser estimado. Por ejemplo, se\(\phi_{H}\) tiene que estimar cuando se resuelve el balance energético con el objetivo de evaluar la temperatura del aire interior en condiciones de límite específicas dadas. Una manera fácil de estimar\(\phi_{H}\) es considerar la capacidad de calentamiento reportada en la ficha técnica del equipo para calefacción suplementaria.
Más detalles sobre los sistemas de calefacción suplementarios se describen a continuación, en la sección de Aplicación.
Flujo de calor de la radiación solar (\(\phi_{H}\))
El flujo de calor debido a la radiación solar depende de la temporada, la ubicación de la granja y las características del edificio. En términos generales, el flujo de calor solar se puede dividir en dos términos de la siguiente manera (International Organization for Standardization, 2017):
\[ \phi_{sol} = \sum^{q}_{n=1}\phi_{sol,op,q} + \sum^{k}_{n=1} \phi_{sol,gl,k} \]
donde\(\phi_{sol,op,q}\) = el calor fluye sobre las q superficies opacas (por ejemplo, paredes y techos) (W)
\(\phi_{sol,gl,k}\)= flujos de calor en las k superficies acristaladas (ventanas) (W)
Para una superficie opaca genérica\(\phi_{sol,op,q}\) se calcula como:
\[ \phi_{sol, op,q} = A_{q} \cdot U_{q} \cdot \alpha_{q} \cdot R_{ex} \cdot I_{sol,q} \cdot F_{sh,q} \]
donde\(\alpha_{q}\) = coeficiente de absorción solar de la superficie considerada dependiendo del color de la superficie (0.3 para colores claros, 0.9 para colores oscuros)
\(R_{ex}\)= resistencia al calor de la superficie externa (m 2 K −1 W −1), generalmente asumida igual a 0.04 m 2 K −1 W −1
\(I_{sol,q}\)= irradiancia solar incidente en la superficie considerada (W m −2)
F sh, q = factor de corrección de sombreado
Para una superficie vidriada genérica k,\(\phi_{s,gl,k}\) se calcula como:
\[ \phi_{s,gl,k} = A_{k} \cdot g_{gl} \cdot I_{sol,k} \cdot (1-F_{fr}) \cdot F_{sh,k} \cdot F_{sh,gl,k} \]
donde\(g_{gl}\) = transmitancia total de energía solar de la superficie transparente
\(F_{fr}\)= fracción de área de cuadro
\(F_{sh,gl,k}\)= factor de reducción de sombreado para provisiones móviles de sombreado
Los factores de sombreado tanto para componentes opacos como acristalados pueden excluirse para la mayoría de las viviendas ganaderas porque aumentan la complejidad del cálculo, pero no afectan en gran medida los resultados.
Flujo de calor debido al sistema de ventilación (\(\phi_{v}\))
La carga de calor debida al sistema de ventilación se puede expresar como
\[ \phi_{v} = \rho_{air} \cdot c_{air} \cdot \dot{V} \cdot (T_{air,sup}-T_{air,i}) \]
donde\(\rho_{air}\) = densidad de masa volumétrica del aire (kg m −3)
\(c_{air}\)= capacidad calorífica específica del aire (W h kg −1 K −1)
\(\dot{V}\)= caudal de ventilación (m 3 h −1)
\(T_{air,sup}\)= temperatura del aire de suministro (°C)
En la estación fría,\(T_{air,sup}\) suele tener el mismo valor de\(T_{air,o}\), ya que la ventilación utiliza aire exterior. En la estación cálida,\(T_{air,sup}\) podría tener valores inferiores a\(T_{air,o}\), ya que el aire exterior se enfría antes de entrar al interior del edificio. El valor de\(T_{air,sup}\) puede estimarse utilizando la efectividad de saturación directa\(\varepsilon\) (%) de un sistema de almohadilla evaporativa, calculado como (ASHRAE, 2012):
\[ \varepsilon = 100 \cdot \frac{T_{air,o,db}-T_{air,sup,bd}}{T_{air,o,db}-T_{air,o,wb}} \]
donde\(T_{air,o,db}\) = temperatura del aire exterior con bulbo seco (°C)
\(T_{air,sup,db}\)= temperatura de bulbo seco del aire de suministro que sale de la almohadilla de enfriamiento (°C)
\(T_{air,o,wb}\)= temperatura de bulbo húmedo del aire exterior que entra en la almohadilla (°C)
La Ecuación 5.2.20 se puede reorganizar para estimar la temperatura del suministro de aire (\(T_{air,sup,db}\)) en presencia de almohadillas evaporativas para su uso en la Ecuación 5.2.19.
Aplicaciones
Los conceptos describen las bases para calcular el balance energético de una casa de animales simple. Estas suelen ser estructuras bastante sencillas construidas con diseños estándar, que difieren en todo el mundo pero que cumplen una función similar de hacer que la producción animal sea más eficiente para el agricultor. El cálculo para el diseño de la casa de animales (la estructura de control) necesariamente asume un ambiente típico o promedio. En realidad, el clima y la gestión de la producción significan que tiene que haber componentes del sistema que sean dinámicos y respondan a las condiciones externas. En esta sección se discute parte de la tecnología requerida para ayudar a mantener un ambiente de vida seguro y eficiente para los animales.
Calefacción Casas de Animales
Sistemas de Calefacción Suplementarios
En clima frío, puede ser necesaria una fuente de calor suplementaria para alcanzar la temperatura de consigna del aire para garantizar condiciones de vida adecuadas para el ganado. Esto es común al inicio del ciclo productivo cuando la producción de calor animal es pequeña y en estaciones frías del año. Este consumo de energía representa una fracción mayor del consumo total de energía directa de la finca (Cuadro 5.2.3) y puede calcularse usando la Ecuación 5.2.3.
Los sistemas de calefacción suplementarios se pueden clasificar en sistemas de calefacción localizada y de calefacción de espacios. Los sistemas de calefacción localizados crean variaciones de temperatura en las zonas donde se crían los animales. Esto permite que los animales jóvenes se muevan a una zona para un óptimo confort térmico. Para diseñar un sistema de calefacción localizado, el término\(\phi_{m}\) (como se usa en la Ecuación 5.2.1) tendría que ser factorizado en el cálculo para tener en cuenta el flujo de calor entre las zonas internas. El calentamiento localizado generalmente usa calor radiante, como lámparas infrarrojas (para lechones) o calentadores radiantes catalíticos de gas infrarrojo (para pollos de engorde). Estos sistemas emiten 70% de su calor por radiación y el 30% restante por convección; el componente de radiación calienta directamente los animales y el suelo mientras que el componente de convección calienta el aire.
Los sistemas de calefacción de espacios crean un ambiente térmico más uniforme. Son más fáciles de diseñar, administrar y controlar que los sistemas de calefacción localizados, pero tienden a tener un mayor consumo de energía. La calefacción de espacios generalmente se basa en un sistema de convección que utiliza aire caliente. El calor se produce en calderas u hornos y luego se transfiere al edificio cuando es necesario.
Una alternativa es utilizar calefacción directa de aire en la casa. La calefacción directa puede ser más económica de instalar, pero requiere más mantenimiento para lidiar con contaminantes, polvo y humedad (Lindley y Whitaker, 1996). Además, existe la necesidad de ventilar los humos de escape y CO 2 por lo que se tienen que incrementar los caudales de ventilación, requiriendo mayor consumo de energía (Costantino et al., 2020). En otros edificios agrícolas, como los invernaderos, el aire caliente se recircula para disminuir el consumo de energía. En las casas ganaderas esta práctica no es muy recomendable ya que la concentración de contaminantes que se producen en el recinto empeora aún más el IAQ.
| Casa Ganadera | Operación | Porcentaje de Energía Eléctrica (del total) |
Porcentaje de Energía Térmica (del total) |
|---|---|---|---|
|
Casas de pollos de engorde |
ventilación |
39% |
- |
|
calefacción suplementaria |
27% |
96% |
|
|
iluminación |
9% |
- |
|
|
distribución de alimentación |
20% |
- |
|
|
distribución de basura y eliminación de estiércol |
- |
3% |
|
|
transporte y eliminación de estiércol |
- |
1% |
|
|
recolección y empaque de productos |
5% |
- |
|
|
Gallinas ponedoras |
ventilación |
44% |
- |
|
calefacción suplementaria |
- |
- |
|
|
iluminación |
15% |
- |
|
|
distribución de alimentación |
5% |
- |
|
|
distribución de basura y eliminación de estiércol |
2% |
33% |
|
|
tratamiento de estiércol |
27% |
- |
|
|
transporte y eliminación de estiércol |
- |
67% |
|
|
recolección y empaque de productos |
7% |
- |
|
|
Casas de Cerdo |
ventilación y calefacción suplementaria |
48% |
69% |
|
iluminación |
2% |
- |
|
|
preparación de alimentación |
11% |
- |
|
|
distribución de alimentación |
19% |
- |
|
|
cuidado de basura y eliminación de estiércol |
4% |
1% |
|
|
tratamiento de estiércol |
4% |
- |
|
|
transporte y eliminación de estiércol |
12% |
30% |
|
|
Casas de vacas lecheras |
ventilación |
20% |
- |
|
iluminación |
8% |
- |
|
|
alimentación |
17% |
52% |
|
|
ordeño |
16% |
6% |
|
|
enfriamiento de leche |
12% |
- |
|
|
cuidado de la camada |
- |
7% |
|
|
eliminación de estiércol |
8% |
5% |
|
|
tratamiento de estiércol |
18% |
4% |
|
|
transporte y eliminación de estiércol |
1% |
26% |
Los sistemas localizados y de calefacción de espacios se pueden usar juntos o acoplados con calentadores de piso para mejorar el control de las condiciones climáticas interiores. La calefacción por suelo radiante suele ser a través de tuberías de agua caliente o cables de resistencia eléctrica enterrados directamente en el piso, pero esto puede provocar una mayor evaporación y un aumento en el contenido de humedad del aire.
Las fuentes de energía más comunes para calefacción son la electricidad, el gas natural, el propano y la biomasa. La energía solar representa una solución interesante para proporcionar calefacción suplementaria, pero la disponibilidad máxima es durante las estaciones cálidas y durante el día cuando la demanda de calor es más baja.
Sistemas de recuperación de calor
Para mantener la IAQ, el aire interior es reemplazado por aire fresco al aire exterior para diluir los contaminantes y disminuir el contenido de humedad. Durante los períodos de calentamiento, cada metro cúbico de aire fresco que se introduce dentro de la caseta de ganado se calienta para alcanzar la temperatura del punto de ajuste del aire interior. Se pierde el calor del aire agotado. Cuando el aire exterior es frío, calentar el aire fresco requiere una energía considerable; la ventilación representa del 70% al 90% de las pérdidas de calor en las casas ganaderas típicas durante la temporada invernal (ASHRAE, 2011).
Para mejorar el rendimiento energético especialmente en climas fríos, se puede utilizar la recuperación de calor. En las casas ganaderas, los sistemas de recuperación de calor aire-aire se utilizan para transferir calor sensible de una corriente de aire a alta temperatura (aire de escape) a una corriente de aire a baja temperatura (aire de suministro fresco) (ASHRAE, 2012). La transferencia de calor ocurre a través de una superficie de intercambio de calor (una serie de placas o tubos) que separa las dos corrientes de aire, evitando la contaminación cruzada del aire fresco de suministro con los contaminantes en el aire de escape. El tipo más común de intercambiador de calor utilizado en las casas ganaderas es el flujo cruzado (Figura 5.2.3). El calor recuperado aumenta directamente la temperatura del aire fresco de suministro, disminuyendo el calor suplementario que se necesita para alcanzar la temperatura del punto de ajuste del aire interior. Los sistemas de recuperación de calor principalmente transfieren calor sensible pero, bajo ciertas condiciones psicrométricas, incluso parte del calor latente del aire de escape puede ser recuperado. Por ejemplo, cuando el aire exterior es muy frío, el vapor de agua contenido en el aire de escape se condensa y libera el calor latente de condensación aumentando la temperatura del aire fresco.
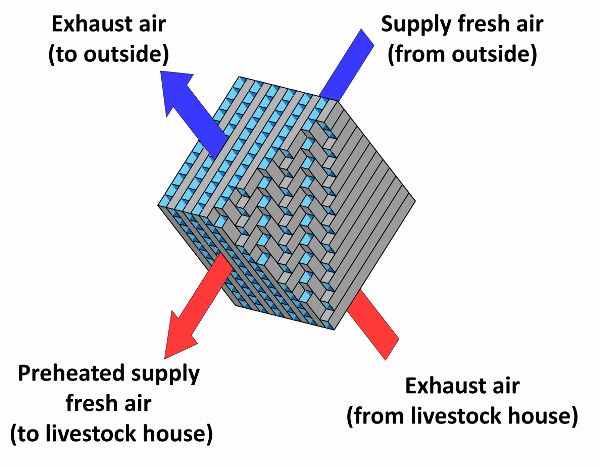
En la práctica, la efectividad del intercambiador de calor es la relación entre la transferencia real de energía y la transferencia máxima posible entre las corrientes de aire (ASHRAE, 1991). En las casas ganaderas esto suele estar entre 60% y 80%, debido a la congelación y acumulación de polvo en las superficies de intercambio de calor (ASHRAE, 2011). Una acumulación de polvo reduce la transferencia de calor entre las corrientes de aire y reduce el caudal. Además, los gases y la humedad en el aire de escape pueden dañar la superficie de intercambio de calor. Los controles de filtración, lavado automático, aislamiento y descongelación se pueden utilizar para evitar problemas con el intercambio de calor.
Enfriamiento de Casas de Animales
Sistemas de Refrigeración
En condiciones más cálidas, se requiere enfriamiento para reducir la temperatura del aire interior y aliviar el estrés por el calor de los animales. El flujo de aire impulsado por ventiladores se utiliza para eliminar el calor generado por los animales y de la radiación solar. Con alta temperatura del aire interior y en situaciones de estrés por calor, se prefieren mayores velocidades del aire alrededor de los animales porque la temperatura de la piel de los animales se reduce a través del creciente intercambio de calor convectivo.
Cuando la diferencia entre las temperaturas del aire exterior y el interior es pequeña, la ventilación de enfriamiento es menos efectiva porque los caudales de aire necesarios requieren velocidades de aire demasiado grandes para la comodidad de los animales. Para superar este problema, se puede usar enfriamiento por agua y enfriamiento evaporativo (Lindley y Whitaker, 1996). El enfriamiento del agua consiste en rociar o gotear agua directamente sobre los animales para eliminar el calor de sus cuerpos a través de la evaporación. El enfriamiento evaporativo utiliza el calor del aire interior para vaporizar el agua y así disminuir la temperatura del aire interior con un sistema de nebulización o almohadillas evaporativas. Los nebulización liberan una niebla de pequeñas gotas de agua directamente dentro del recinto. Las almohadillas evaporativas se utilizan en casas ganaderas con sistemas de ventilación por escape (Figura 5.2.4). En estos sistemas, los extractores fuerzan el aire interior creando una diferencia de presión negativa entre el interior y el exterior de la casa. Esta diferencia de presión tira el aire fresco del exterior dentro de la casa a través de las almohadillas evaporativas, disminuyendo su temperatura algunos grados en función de la efectividad de saturación directa,\(\varepsilon\) (ASHRAE, 2012) (Ecuación 5.2.20). Desde un punto de vista técnico,\(\varepsilon\) es la característica más emocionante de una almohadilla evaporativa, y oscila entre 70% y 95% para almohadillas evaporativas disponibles comercialmente. Este valor es directamente proporcional al grosor de la almohadilla (de 0.1 a 0.3 m) (ASHRAE, 2012) e inversamente proporcional a la velocidad del aire a través de la almohadilla. Las eficiencias más altas son con una velocidad del aire entre 1.0 y 1.4 m s −1 (ASHRAE, 2011). El valor de también\(\varepsilon\) está influenciado por la edad y el mantenimiento de la almohadilla;\(\varepsilon\) puede disminuir a 30% en almohadillas viejas y mal mantenidas (Costantino et al., 2018).
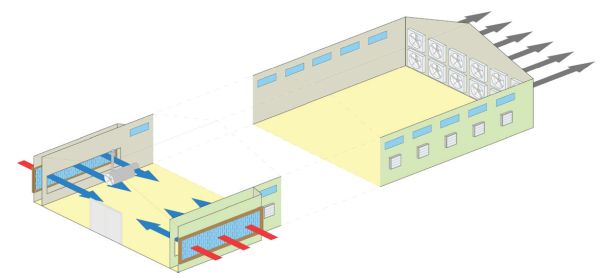
Las almohadillas evaporativas afectan el consumo de energía de dos maneras. Por un lado, disminuyen la temperatura del aire que se utiliza para ventilar la casa, lo que significa una reducción en el caudal de ventilación necesario para mantener la temperatura de consigna del aire interior. Por otro lado, incrementan la diferencia de presión entre el interior y el exterior de la casa, por lo que para el mismo caudal de aire, los ventiladores en una caseta ganadera equipada con almohadillas evaporativas requieren un mayor consumo de electricidad. Finalmente, el uso de almohadillas evaporativas requiere energía eléctrica adicional debido a las bombas de circulación utilizadas para mover el agua del almacenamiento para humedecer la parte superior de las almohadillas.
Sistemas de Ventilación
La efectividad de la ventilación dentro de una casa ganadera depende de la selección, instalación y operación de los equipos de ventilación, como entradas de aire, salidas, sistemas de control y ventiladores.
Los ventiladores se clasifican como centrífugos o axiales, según la dirección del flujo de aire a través del impulsor (ASHRAE, 2012). Los ventiladores axiales extraen aire paralelo al eje del eje (alrededor del cual giran las palas) y lo extraen en la misma dirección. Los ventiladores centrífugos extraen aire por deflexión y fuerza centrífuga. En ventiladores centrífugos el aire entra junto al eje debido a la rotación del impulsor y luego se mueve perpendicularmente desde el eje hasta la abertura donde se agota. Los ventiladores axiales se utilizan generalmente en las viviendas para ganado porque el objetivo principal es proporcionar una alta tasa de flujo de aire y no crear una diferencia de alta presión a través del ventilador. Los ventiladores provocan un consumo considerable de energía en las casas ganaderas (Costantino et al., 2016), como se muestra en la Tabla 5.2.3, pero generalmente se compran con base en el costo de compra, no en los costos de operación. Cuando se instalan ventiladores en las casas ganaderas, se tiene que esperar una reducción en la eficiencia debido al desgaste de las conexiones mecánicas (ASHRAE, 2012).
Ejemplos
Ejemplo\(\PageIndex{1}\)
Ejemplo 1: Flujo de calor a través de la envolvente de un edificio
Problema:
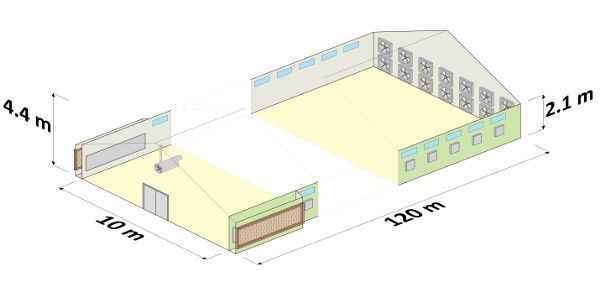
Determinar el flujo total de calor de transmisión en estado estacionario a través de la envolvente del edificio del asador de techo a dos aguas presentado en la Figura 5.2.5. Las propiedades termofísicas de los elementos envolventes se muestran en el Cuadro 5.2.4. Para el cálculo, supongamos que la temperatura del aire interior es de 23°C y la temperatura del aire exterior es de 20°C.
Solución
El flujo total de calor de transmisión a través de la envolvente debe calcularse mediante la Ecuación 5.2.15. En la suma, deben considerarse todos los elementos envolventes de la casa de pollos de engorde. En esta casa de pollos de engorde, los diversos productos\((b_{tr,j} \cdot U_{j} \cdot A_{j})\) de la suma de la Ecuación 5.2.15 son:
Elemento de construcción |
Área (m 2) |
U (W m −2 k −1) |
b tr (-) |
|---|---|---|---|
|
Muro Norte |
195 |
0.81 |
1 |
|
Muralla Sur |
195 |
0.81 |
1 |
|
Muros Oriente |
18 |
0.81 |
1 |
|
Muro Oeste |
33 |
0.81 |
1 |
|
Techo |
1320 |
1.17 |
1 |
|
Piso |
1200 |
0.94 |
0.45 |
|
Puerta (este) |
15 |
1.51 |
1 |
|
Ventanas Norte |
57 |
3.60 |
1 |
|
Ventanas Sur |
57 |
3.60 |
1 |
\( \phi_{tr} = [\sum^{n}_{j=1}(b_{tr,j} \cdot U_{j} \cdot A_{j})] \) (Equation \(\PageIndex{15}\))
\( b_{tr,walls} \cdot U_{walls} \cdot A_{walls} = 1 \cdot 0.81 \frac{W}{m^{2} \cdot K} \cdot 441 m^{2} = 357.2 \frac{W}{K} \)
\( b_{tr,roof} \cdot U_{roof} \cdot A_{roof} = 1 \cdot 1.17 \frac{W}{m^{2} \cdot K} \cdot 1320 m^{2} = 1544.4 \frac{W}{K} \)
\( b_{tr, doors} \cdot U_{doors} \cdot A_{doors} = 1 \cdot 1.51 \frac{W}{m^{2} \cdot K} \cdot 15 m^{2} = 22.7 \frac{W}{K} \)
\( b_{tr, windows} \cdot U_{windows} \cdot A_{windows} = 1 \cdot 3.60 \frac{W}{m^{2} \cdot K} \cdot 114 m^{2} = 410.4 \frac{W}{K} \)
El valor U del piso de la casa de pollos de engorde es 0.94 W m −2 K −1. Este valor se calculó considerando que el piso fue realizado por una solera de hormigón armado y una lámina impermeabilizante directamente en contacto con el suelo. En el flujo de calor de transmisión vía tierra, se tiene que considerar el\(b_{tr}\) coeficiente. Considerando que el piso de la casa de pollos de engorde está en contacto directo con el suelo, se\(b_{tr,floor}\) puede suponer igual a 0.45 (valor de la Tabla 5.2.2). El cálculo es:
\( b_{tr, floor} \cdot U_{floor} \cdot A_{floor} = 0.45 \cdot 0.94 \frac{W}{m^{2} \cdot K} \cdot 1200 m^{2} = 507.6 \frac{W}{K} \)
Considerando los valores previamente calculados, la suma es:
\( \sum^{n}_{j=1} (b_{tr,j} \cdot U_{j} \cdot A_{j}) = 2842.3 \frac{W}{K} \)
Finalmente, el flujo de calor se puede calcular considerando la diferencia de temperatura entre interior y exterior como:
Ejemplo\(\PageIndex{2}\)
Ejemplo 2: Flujo de calor sensible en una casa de pollos de engorde
Problema:
Determinar el flujo de calor sensible producido a nivel de casa por una manada de 14,000 pollos de engorde a una temperatura del aire interior de 23°C, el peso promedio de los pollos de engorde es de 1.3 kg.
Solución
La producción total de calor\(\phi_{a,tot}\) de una manada de pollos de engorde a una temperatura del aire interior de 20°C se define por la Ecuación 5.2.6 que dice
\( \phi_{a,tot}=10.62 \cdot w_{a}^{0.75} \cdot n_{a} \)(Ecuación\(\PageIndex{6}\))
Considerando las condiciones de límite dadas, la Ecuación 5.2.6 se convierte en:
\( \phi_{a,tot}=10.62 \cdot 1.3^{0.75} \cdot 14,000 = 181,013.1\ W \)
Antes de calcular\(\phi_{a}\), n hpu tiene que calcularse de acuerdo con la Ecuación 5.2.14:
\( n_{hpu} = \frac{\phi_{a,tot}}{1000} \)(Ecuación\(\PageIndex{14}\))
\( n_{hpu} = \frac{181,031.1\ W}{1000 \frac{W}{hpu}} = 181.01\ hpu \)
Finalmente,\(\phi_{a}\) calculado a 23°C de\(T_{air,i}\) es (a partir de la Ecuación 5.2.10):
\( \phi_{a} = \{0.61 \cdot [1000+20 \cdot(20-T_{air,i})] -0.228 \cdot T_{air,i}^{2} \} \cdot n_{npu} \)(Ecuación\(\PageIndex{10}\))
\( \phi_{a} = \{0.61 \cdot [1000+20 \cdot(20-23^\circ C)] -0.228 \cdot (23^\circ C)^{2} \} \cdot 181.01 = 81,959.2\ W \)
El rebaño de pollos de engorde en este ejemplo produce alrededor de 82 kW de calor sensible.
Ejemplo\(\PageIndex{3}\)
Ejemplo 3: Flujo de calor basado en energía solar
Problema:
Determinar el valor de\(\phi_{sol}\) considerar las condiciones de contorno que se muestran en el Cuadro 5.2.5 y usar la misma casa de pollos de engorde de los Ejemplos 5.2.1 y 5.2.2.
Solución
El primer paso para determinar\(\phi_{sol}\) es calcular\(\phi_{sol,op}\) para cada elemento de construcción opaco de acuerdo con la Ecuación 5.2.17, como:
Elemento de construcción |
Área (m 2) |
U (W m −2 k −1) |
α (-) | g gl (-) | I sol (W m −2) |
|---|---|---|---|---|---|
|
Muro Norte |
195 |
0.81 |
0.3 |
- |
142 |
|
Muralla Sur |
195 |
0.81 |
0.3 |
- |
559 |
|
Muros Oriente |
18 |
0.81 |
0.3 |
- |
277 |
|
Muro Oeste |
33 |
0.81 |
0.3 |
- |
142 |
|
Techo |
1320 |
1.17 |
0.9 |
- |
721 |
|
Piso |
1200 |
0.94 |
- |
- |
- |
|
Puerta (este) |
15 |
1.51 |
0.9 |
- |
277 |
|
Ventanas Norte |
57 |
3.60 |
- |
0.6 |
142 |
|
Ventanas Sur |
57 |
3.60 |
- |
0.6 |
559 |
\( \phi_{sol,op,q} = A_{q} \cdot U_{q} \cdot \alpha_{q} \cdot R_{ex} \cdot I_{sol,q} \cdot F_{sh,q} \) (Equation \(\PageIndex{17}\))
\( \phi_{sol,op,wall, N} = 195 m^{2} \cdot 0.81 \frac{W}{m^{2}\cdot K} \cdot 0.3 \cdot 0.04 \frac{m^{2} \cdot K}{W} \cdot 142 \frac{W}{m^{2}} = 269.1\ W \)
\( \phi_{sol,op,wall, S} = 195 m^{2} \cdot 0.81 \frac{W}{m^{2}\cdot K} \cdot 0.3 \cdot 0.04 \frac{m^{2} \cdot K}{W} \cdot 559 \frac{W}{m^{2}} = 1059.5\ W \)
\( \phi_{sol,op,wall, E} = 18 m^{2} \cdot 0.81 \frac{W}{m^{2}\cdot K} \cdot 0.3 \cdot 0.04 \frac{m^{2} \cdot K}{W} \cdot 277 \frac{W}{m^{2}} = 48.5\ W \)
\( \phi_{sol,op,wall, E} = 33 m^{2} \cdot 0.81 \frac{W}{m^{2}\cdot K} \cdot 0.3 \cdot 0.04 \frac{m^{2} \cdot K}{W} \cdot 142 \frac{W}{m^{2}} = 45.5\ W \)
\( \phi_{sol,op,wall, Roof} = 1320 m^{2} \cdot 1.17 \frac{W}{m^{2}\cdot K} \cdot 0.9 \cdot 0.04 \frac{m^{2} \cdot K}{W} \cdot 721 \frac{W}{m^{2}} = 40,086.4\ W \)
\( \phi_{sol,op,wall, Roof} = 15 m^{2} \cdot 1.51 \frac{W}{m^{2}\cdot K} \cdot 0.9 \cdot 0.04 \frac{m^{2} \cdot K}{W} \cdot 277 \frac{W}{m^{2}} = 225.9\ W \)
La suma de los\(\phi_{sol,op,q}\) valores calculados es:
\( \sum^{q}_{n=1}\phi_{sol,op,q} = 41,734.9\ W \)
Las cargas de calor solar en los componentes acristalados se pueden estimar usando la Ecuación 5.2.18:
\( \phi_{s,gl,k}=A_{k} \cdot g_{gl} \cdot I_{sol,k} \cdot (1-F_{fr}) \cdot F_{sh,k} \cdot F_{sh,gl,k} \)(Ecuación\(\PageIndex{18}\))
Teniendo en cuenta las condiciones de límite dadas,\(\phi_{sol,gl}\) para los elementos acristalados se pueden calcular como:
\( \phi_{sol,gl,win,N} = 57\ m^{2} \cdot 0.6 \cdot 142 \frac{W}{m^{2}} \cdot (1-0.2) = 3885.1\ W \)
\( \phi_{sol,gl,win,S} = 57\ m^{2} \cdot 0.6 \cdot 559 \frac{W}{m^{2}} \cdot (1-0.2) = 15,294.2\ W \)
La suma de los\(\phi_{sol,gl,k}\) valores calculados es:
\( \sum^{k}_{n=1} \phi_{sol,gl,k} = 19,179.3\ W \)
Finalmente, la carga total de calor solar es:
\( \phi_{sol} = 41,734.9\ W + 19,179.3\ W = 60,914.2\ W \)
Ejemplo\(\PageIndex{4}\)
Ejemplo 4: Caudal de ventilación para el control de temperatura
Problema:
Determinar el caudal de ventilación volumétrica (m 3 h −1) que deben proporcionar los ventiladores de escape de la casa de pollos de engorde para mantener la temperatura del aire interior a 23°C. Para el cálculo, considere la ausencia de flujo de calentamiento suplementario (\(\phi_{H}=0\ W\)) los flujos de calor calculados en Ejemplo 5.2.1 (\(\phi_{tr}\)), Ejemplo 5.2.2 (\(\phi_{a}\)) y Ejemplo 5.2.4 (\(\phi_{sol}\)). La temperatura del aire de suministro es la misma que la del aire exterior (20°C, como en el Ejemplo 5.2.1).
Solución
En los ejemplos anteriores se calcularon los siguientes flujos de calor:
\( \phi_{tr} = -8,526.9\ W = - 8.5\ kW \)
\( \phi_{a} = 81,959.2\ W = 82.0\ kW \)
\( \phi_{sol} = 60,914.2\ W = 60.9\ kW \)
El texto del problema señala que no se presenta ningún flujo de calentamiento suplementario, por lo tanto:
\( \phi_{H} = 0\ kW \)
Considerando las condiciones de límite dadas, el balance energético de la Ecuación 5.2.3 puede escribirse como:
\( 82.0\ kW - 8.5\ kW + 0\ kW + 60.9\ kW + \phi_{v} = 0 \)
Eso se convierte en:
\( \phi_{v} = -134.4\ kW \)
La ecuación 5.2.19 puede expresarse en\(\dot{V}\) (lo desconocido del problema, en kW) como:
\( \dot{V} = \frac{\phi_{v}}{\rho_{air} \cdot c_{air} \cdot (T_{air,sup} - T_{air, i})} \)
El valor de\(\rho_{air}\) se asume igual a 1.2 kg m −3 e\(c_{air}\) igual a 2.8 × 10 −4 kWh kg −1 K −1 (1010 J kg −1 K −1), aunque para un cálculo más detallado\(\rho_{air}\) debe evaluarse en el aire interior dado temperatura y presión atmosférica. El flujo de aire de ventilación se proporciona con aire exterior, por lo tanto,\(T_{air,sup}\) es igual a\(T_{air,o}\). Al ingresar el valor previamente calculado de\(\phi_{v}\), la ecuación anterior dice:
\( \dot{V} = \frac{-134.4\ kW}{1.2 \frac{kg}{m^{3}} \cdot 2.8 \cdot 10^{-4} \frac{kWh}{kg \cdot K} \cdot (20 ^\circ C - 23 ^\circ C)} = 133,333\frac{m^{3}}{h} \)
Para mantener la temperatura requerida del aire interior dentro de la caseta de ganado, alrededor de 133,000 m 3 h −1 de aire fresco al aire libre debe ser proporcionado por el sistema de ventilación.
Créditos de imagen
Figura 1. Fabrizio, E. (CC Por 4.0). (2020). El balance térmico sensible de la ecuación 3 aplicado a una casa ganadera genérica.
Figura 2. Fabrizio, E. (CC Por 4.0). (2020). El balance de masa de vapor de la ecuación 5 aplicado a una casa ganadera genérica.
Figura 3. Costantino, A. (CC Por 4.0). (2020). Diagrama de la superficie de intercambio de calor en un sistema de recuperación de calor aire-aire.
Figura 4. Costantino, A. (CC Por 4.0). (2020). Diagrama de una casa de pollos de engorde equipada con almohadillas evaporativas.
Figura 5. Costantino, A. (CC Por 4.0). (2020). Diagrama de la casa de pollos de engorde de ejemplo con las principales dimensiones geométricas.
Referencias
Albright, L. (1990). Control ambiental para animales y plantas. San José, MI: ASAE.
Estándares ASABE. (2012). ASAE EP270.5 DEC1986: Diseño de sistemas de ventilación para refugios avícolas y ganaderos. San José, MI: ASABE.
ASHRAE. (2012). Manual ASHRAE 2012: Sistemas y equipos HVAC. Atlanta, GA: ASHRAE.
ASHRAE. (2011). Manual ASHRAE 2011: Aplicaciones HVAC. Atlanta, GA: ASHRAE.
ASHRAE. (1991). Norma ANSI/ ASHRAE 84-1991: Método de prueba de intercambiadores de calor aire-aire. Atlanta, GA: ASHRAE.
CIGR. (1999). CIGR manual de ingeniería agrícola (Vol. II). San José, MI: ASAE.
Costantino, A., Ballarini, I., & Fabrizio, E. (2017). Comparación entre métodos simplificados y detallados para el cálculo de las necesidades energéticas de calefacción y refrigeración de las viviendas ganaderas: Un estudio de caso. En Aplicaciones de Simulación de Edificios (pp. 193-200). Bolzano, Italia: Universidad Libre de Bozen-Bolzano.
Costantino, A., Fabrizio, E., Biglia, A., Cornale, P., & Battaglini, L. (2016). Uso de energía para el control climático de las casas de animales: El estado del arte en Europa. Energía Proc. 101, 184-191. https://doi.org/10.1016/j.egypro.2016.11.024
Costantino, A., Fabrizio, E., Ghiggini, A., & Bariani, M. (2018). Climatización en pollos de engorde: Un modelo térmico para el cálculo del uso de energía y las condiciones ambientales en interiores. Construcción Energética. 169, 110-126. https://doi.org/10.1016/j.enbuild.2018.03.056
Costantino, A., Fabrizio, E., Villagrá, A., Estellés, F., & Calvet, S. (2020). La reducción de las concentraciones de gas en los pollos de engorde a través de la ventilación: Evaluación del consumo de energía térmica y eléctrica. Biosyst. Ing. https://doi.org/10.1016/j.biosystemseng.2020.01.002.
Esmay, M. E., & Dixon, J. E. (1986). Control ambiental para edificios agrícolas. Westport, CT: AVI.
Comité Europeo de Normalización. (2009). EN 12831: Sistemas de calefacción en edificios—Método para el cálculo de la carga térmica de diseño. Bruselas, Bélgica: CEN.
Comité Europeo de Normalización. (2007). EN 13789: Rendimiento térmico de edificios—Coeficientes de transferencia de calor de transmisión y ventilación—Método de cálculo. Bruselas, Bélgica: CEN.
Hamilton, J., Negnevitsky, M., & Wang, X. (2016). Análisis térmico de un establo ganadero de una sola planta. Adv. Mech. Ing. 8 (4). https://doi.org/10.1177/1687814016643456.
Hellickson, M. A., & Walker, J. N. (1983). Ventilación de estructuras agrícolas. San José, MI: ASAE.
ISO. (2017). ISO 52016-1:2017: Rendimiento energético de edificios—Necesidades energéticas para calefacción y refrigeración, temperaturas internas y cargas de calor sensibles y latentes—Parte 1: Procedimientos de cálculo. Organización Internacional de Normalización.
Liberati, P., & Zappavigna, P. (2005). Un modelo informático para la optimización del clima interno en el diseño de alojamientos de animales. En Ambiente Ganadero VII, Proc. Int. Symp. San José, MI: ASABE.
Lindley, J. A., & Whitaker, J. H. (1996). Edificaciones y estructuras agrícolas. San José, MI: ASAE.
Servicio de Plan Medio Oeste. (1987). Manual de estructuras y medio ambiente (11ª ed.). Ames, IA: Servicio de Plan Medio Oeste.
OCDE. (2008). Desempeño ambiental de la agricultura en países de la OCDE desde 1990. París, Francia: OCDE.
Panagakis, P., & Axaopoulos, P. (2008). Comparación de estrategias de nebulización para la cría de cerdos mediante simulaciones para determinar índices aparentes de estrés térmico. Biosyst. Ing. 99 (1), 112-118. https://doi.org/10.1016/j.biosystemseng.2007.10.007.
Pedersen, S., & Sällvik, K. (2002). 4º informe del grupo de trabajo sobre climatización de casas de animales: producción de calor y humedad a nivel animal y doméstico. Horsens, Dinamarca: Instituto Danés de Ciencias Agrícolas.
Rossi, P., Gastaldo, A., Riva, G., & de Carolis, C. (2013). Progetto re Sole—linee guida per il risparmio energetico e per la produzione di energia da fonte solare negli allevamenti zootecnici (en italiano). Reggio Emilia, Italia: CRPA.
St-Pierre, N. R., Cobanov, B., & Schnitkey, G. (2003). Pérdidas económicas por estrés térmico por las industrias ganaderas estadounidenses. J. Lácteos Sci. 86, E52-E77. https://doi.org/10.3168/jds.s0022-0302(03)74040-5.


