3.3: Ajuste de una función de distribución a los datos

En esta sección se analiza el uso de datos para determinar la función de distribución que se utilizará para modelar una cantidad aleatoria, así como los valores para los parámetros de distribución. Se discuten algunas dificultades comunes para obtener y usar datos. Se dan las funciones de distribución comunes utilizadas en los modelos de simulación. Ley (2007) proporcionan una discusión en profundidad sobre este tema, incluyendo funciones adicionales de distribución. Se presenta un procedimiento basado en software para usar datos en la selección de una función de distribución.

3.3.1 Algunos problemas comunes de datos

Es fácil suponer que los datos son abundantes y fácilmente disponibles en un sistema de información corporativa. Sin embargo, a menudo no es así. Se discuten algunos problemas con la obtención y el uso de datos.

1. Los datos están disponibles en el sistema de información corporativa pero nadie en el equipo del proyecto tiene permiso para acceder a los datos.

   Normalmente, este problema se resuelve obteniendo el permiso necesario. No obstante, tal vez no sea posible obtener este permiso de manera oportuna. En este caso, los procedimientos para determinar una función de distribución en ausencia de datos deben utilizarse al menos inicialmente hasta que se puedan obtener los datos.

2. Los datos están disponibles pero deben transformarse en valores que midan la cantidad de interés.

   Por ejemplo, supongamos que el tiempo de envío del camión entre una planta y un cliente es de interés. El sistema de información de la compañía registra los siguientes horarios de reloj para cada viaje en camión: salida de la planta, llegada al cliente, salida del cliente y llegada a la planta. Los siguientes valores se pueden calcular directamente a partir de esta información para cada viaje en camión: tiempo de viaje de la planta al cliente, retraso de tiempo en el cliente, tiempo de viaje del cliente a la planta.

   Este ejemplo plantea algunas otras preguntas. ¿Hay alguna razón para creer que el tiempo de viaje de la planta al cliente es diferente al tiempo de viaje del cliente a la planta? Si no, los dos conjuntos de valores podrían combinarse y se podría determinar una sola distribución a partir de todos los valores. Si existe una razón conocida de que los tiempos de viaje son diferentes, los dos conjuntos de datos deben analizarse por separado. Por supuesto, un análisis estadístico, como el método par t discutido en el capítulo 4, podría utilizarse para evaluar si existe alguna diferencia estadísticamente significativa en los tiempos medios de viaje.

   ¿Cuál es el nivel de detalle incluido en el modelo? Puede ser necesario incluir en el modelo las tres veces enumeradas en el párrafo anterior. Alternativamente, solo se podría incluir el tiempo total de ida y vuelta, la diferencia entre la salida de la planta y la llegada a la planta.

3. Todos los datos necesarios están disponibles, pero solo de múltiples fuentes.

   Cada una de las múltiples fuentes puede medir cantidades de diferentes maneras o en diferentes momentos. Por lo tanto, los datos de diferentes fuentes necesitan ser coherentes entre sí. Esto es discutido por Standridge, Pritkser y Delcher (1978).

   Por ejemplo, la cantidad de ventas de un producto químico se mide en libras de producto en el sistema de información de ventas y en volumen de producto en el sistema de información de envío. El modelo debe medir la cantidad de producto ya sea en libras o volumen. Supongamos que se eligieron libras. Los datos en el sistema de información de envío podrían ser utilizados después de dividirlos por la densidad del producto (libras/galón).

   Considera otro ejemplo. Se utiliza un pronóstico de ventas para establecer el volumen promedio de demanda de un producto utilizado en un modelo. El pronóstico de ventas para el producto es un valor único. Se necesita una distribución de la demanda de productos. Una distribución se determina utilizando datos históricos de ventas. El pronóstico de ventas se utiliza como la media de una distribución en lugar de la media calculada a partir de datos históricos. Esto supone que sólo la media cambiará en el futuro. Los otros parámetros de distribución como la varianza así como la familia de distribución particular, normal por ejemplo, seguirán siendo los mismos.

4. Todos los datos están “sucios”.

   Es tentador suponer que los datos de un sistema de información informática pueden ser utilizados sin más examen o procesamiento. Este no suele ser el caso. Muchos mecanismos de recolección de datos no toman en cuenta las anomalías que ocurren en las operaciones diarias del sistema.

   Por ejemplo, un sistema automatizado registra el volumen de un producto líquido producido cada día. Este volumen de producción se modela como una sola cantidad aleatoria. El volumen de producción registrado para todos los días es mayor a cero. No obstante, en pocos días es dos órdenes de magnitud menos que el resto de los días. Se determinó que estos bajos volúmenes significaron que la planta estaba baja por el día. Así, el volumen de producción fue modelado por una función de distribución para los días en que la planta estuvo operando y cero para los días restantes. Cada día en el modelo de simulación, se hizo una elección aleatoria de si la planta estaba operando o no ese día. La probabilidad de que la planta estuviera operando se estimó a partir del conjunto de datos como porcentaje de días operativos/número total de días.

3.3.2 Funciones de distribución más utilizadas en un modelo de simulación

En esta sección se presentan las funciones de distribución más utilizadas en los modelos de simulación. Se describe el uso típico de cada distribución. Se da un resumen de cada distribución.

En la sección 3.2.1 se presentaron las funciones de distribución utilizadas en ausencia de datos. Las distribuciones uniformes y triangulares normalmente solo se utilizan en este caso. También se utiliza la distribución beta. La beta también es útil modelar tiempos de tareas del proyecto.

Además, se discutió el uso de la distribución exponencial para modelar el tiempo entre llegadas de entidades. Nuevamente, las condiciones para usar la distribución exponencial son: hay una llegada a la vez, los números de llegadas en intervalos de tiempo disjuntos son independientes, y el tiempo promedio hasta la siguiente llegada no cambia durante el periodo de tiempo de simulación. En algunos casos, esta última suposición no es cierta. Una forma de manejar esta situación se ilustra en el estudio de aplicaciones sobre la gestión del centro de contacto.

Si el sistema ejerce algún control sobre las llegadas, esta información puede ser incorporada en la simulación. Por ejemplo, las llegadas de piezas en bruto a un sistema de fabricación podrían ocurrir cada hora en la hora. El tiempo entre llegadas sería de 1 hora constante. Supongamos que los trabajadores han notado que los espacios en blanco realmente llegan a cualquier lugar entre 5 minutos antes y 5 minutos después de la hora. Así, el proceso de llegada podría modelarse como con un tiempo constante entre llegadas de 1 hora seguido de un retraso distribuido uniformemente de 0 a 10 minutos antes de que comience el procesamiento.

A menudo es importante incluir el fallo de los equipos en un modelo de simulación. Los modelos del tiempo hasta el fracaso se pueden tomar de la teoría de la confiabilidad. La distribución exponencial también se puede utilizar para modelar el tiempo hasta la siguiente avería del equipo si se cumplen las condiciones adecuadas: hay una avería a la vez (para cada pieza del equipo), el número de averías en intervalos de tiempo disjuntos son independientes y el tiempo promedio hasta el siguiente desglose no cambia durante el periodo de tiempo de simulación.

Supongamos que cualquiera de los siguientes es cierto:

1. El tiempo a partir de ahora hasta la falla depende de cuánto tiempo haya estado funcionando el equipo.
2. La falla ocurre cuando falla el primero de muchos componentes o puntos de falla.

Bajo estas condiciones, la distribución de Weibull es un modelo apropiado del tiempo entre fallas. El Weibull también se utiliza para modelar los tiempos de operación. Una distribución de Weibull tiene un límite inferior de cero y se extiende hasta el infinito positivo.

Una distribución de Weibull tiene dos parámetros: un parámetro de forma\(\ \alpha\) > 0 y un parámetro de escala\(\ \beta\) > 0. Tenga en cuenta que la distribución exponencial es un caso especial de la distribución de Weibull para\(\ \alpha\) = 1. En la Figura 3-6 se presenta un resumen de la distribución de Weibull.

Supongamos que el fracaso se debe a un proceso de degradación y es aceptable un requisito matemático de que la degradación en cualquier momento sea una pequeña proporción aleatoria de la degradación hasta ese punto en el tiempo. En este caso la distribución logarítmica normal es apropiada. El lognormal se ha aplicado con éxito en modelar el tiempo hasta el fracaso en procesos químicos y con algunos tipos de crecimiento de grietas. También es útil para modelar tiempos de operación.

La distribución lognormal puede pensarse de la siguiente manera. Si la variable aleatoria X sigue la distribución lognormal entonces la variable aleatoria ln X sigue la distribución normal. Los parámetros de distribución lognormal son la media y desviación estándar de los resultados de la distribución normal de esta operación. Una distribución lognormal varía de 0 a infinito positivo. La distribución logarítmica normal se resume en la Figura 3-7.

Considera los tiempos de operación, inspección, reparación y transporte. En el modelado de actividades automatizadas, estos tiempos pueden ser constantes. Un tiempo constante también podría ser apropiado si se asignara un tiempo estándar a una tarea. Si se trata del esfuerzo humano, generalmente se debe incluir alguna variabilidad y por lo tanto se debe emplear una función de distribución.

El Weibull y lognormal son posibilidades como se mencionó anteriormente. También se podría emplear el gamma. Una distribución gamma tiene dos parámetros: un parámetro de forma\(\ \alpha\) > 0 y un parámetro de escala\(\ \beta\) > 0. Es una de las formas más generales y flexibles de modelar un retardo de tiempo. Tenga en cuenta que la distribución exponencial es un caso especial de la distribución gamma para\(\ \alpha\) = 1.

Figura 3-6: Resumen de la distribución de Weibull.

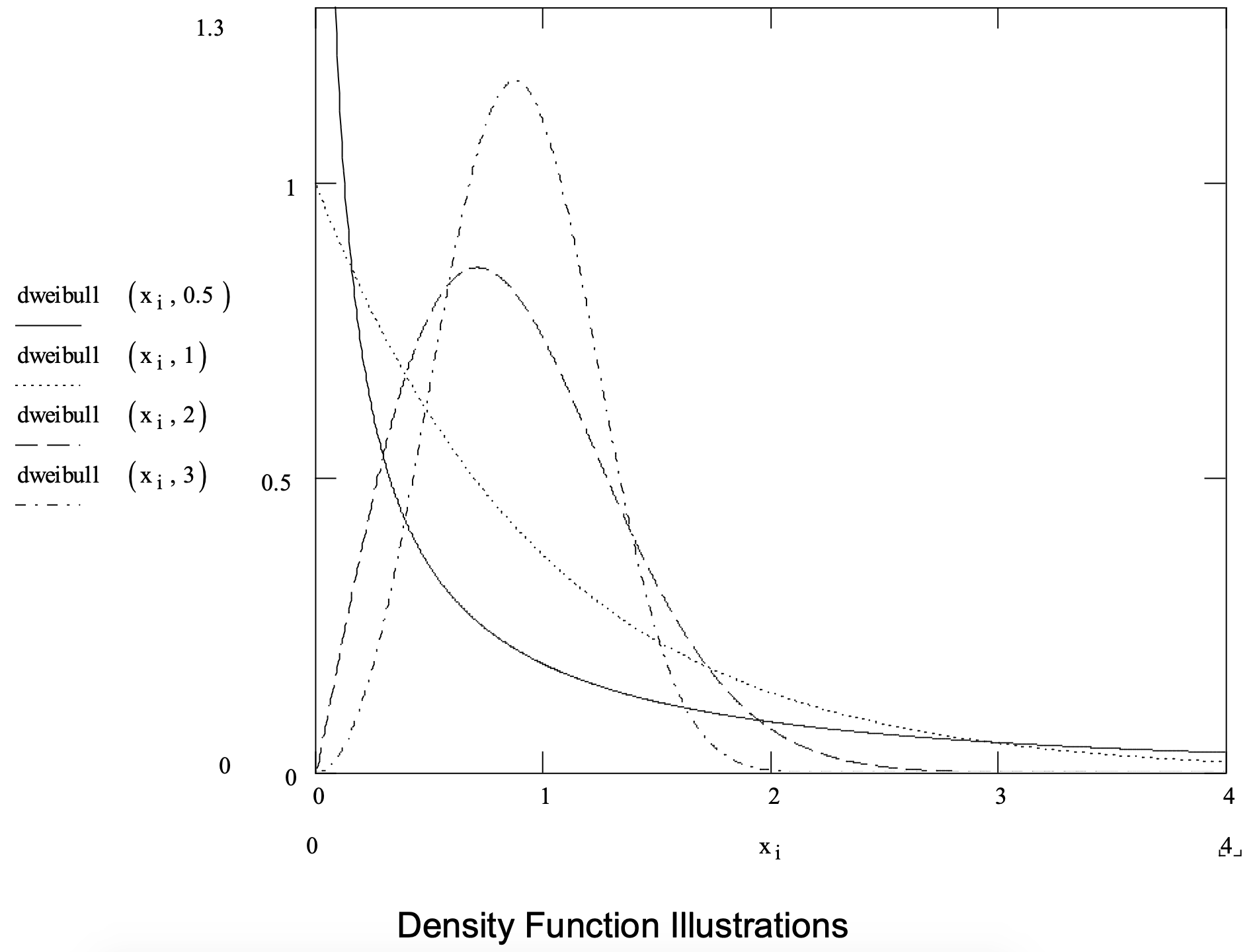
Parámetros:	Parámetro de forma,\(\ \alpha\) > 0, y un parámetro de escala,\(\ \beta\) > 0.
Rango:	[0,\ (\\ infty))
Media:	\(\ \frac{\beta}{\alpha} \Gamma\left(\frac{1}{\alpha}\right),\ where\ Gamma\ is\ the\ gamma\ function.\)
Varianza:	\(\ \frac{\beta^{2}}{\alpha}\left\{2 \Gamma\left(\frac{2}{\alpha}\right)-\frac{1}{\alpha}\left[\Gamma\left(\frac{1}{\alpha}\right)\right]^{2}\right\}\)
Densityfunction:	\(\ f(x)=\alpha \beta^{-\alpha} x^{\alpha-1} e^{-(x / \beta)^{\alpha}} ; x \geq 0\)
Función de distribución:	\(\ F(x)=1-e^{-(x / \beta)^{\alpha}} ; x \geq 0\)
Aplicación:	La distribución Weibull se utiliza para modelar el tiempo entre fallas del equipo así como los tiempos de operación.

Figura 3-7: Resumen de la Distribución Lognormal.

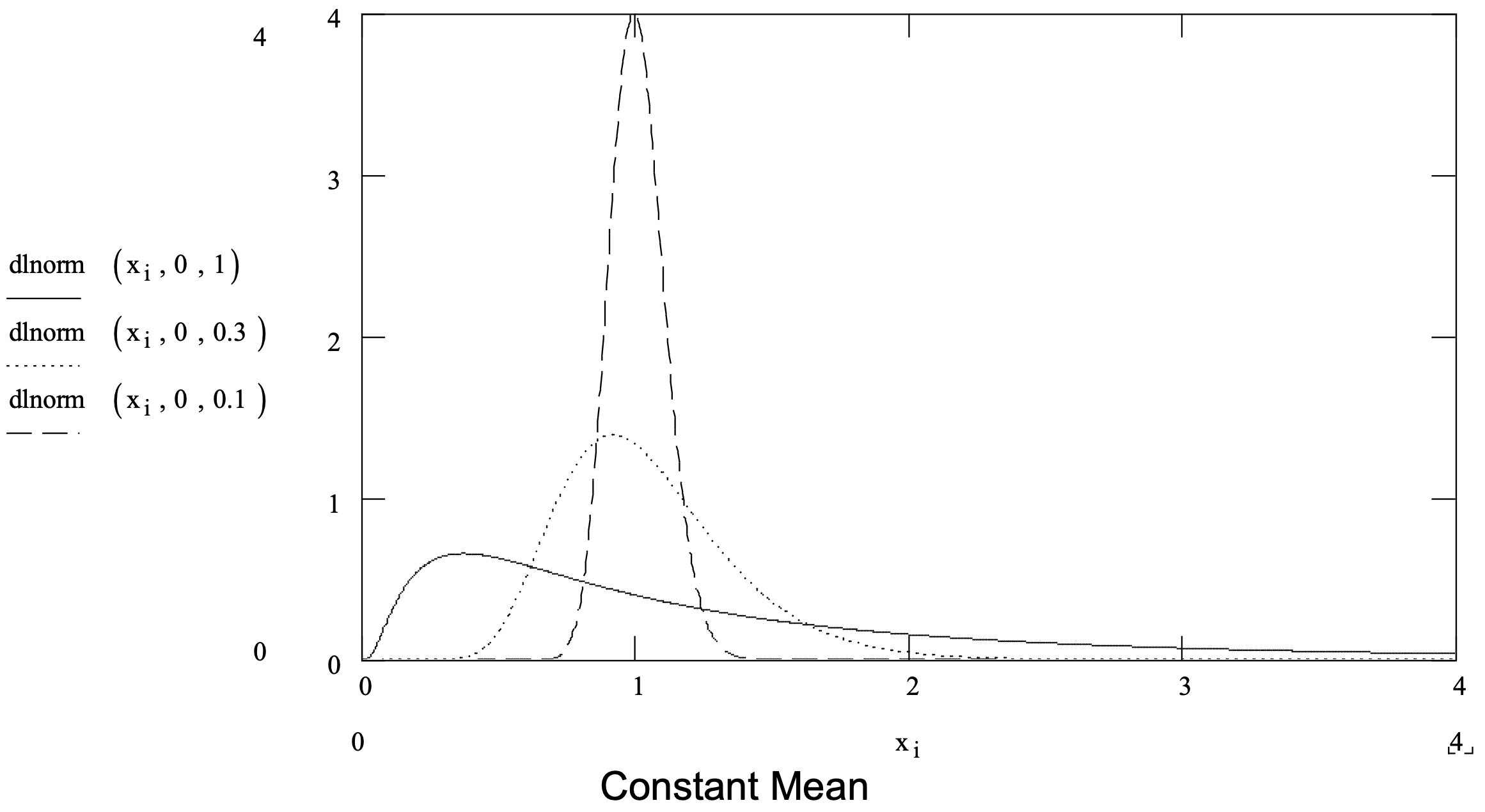
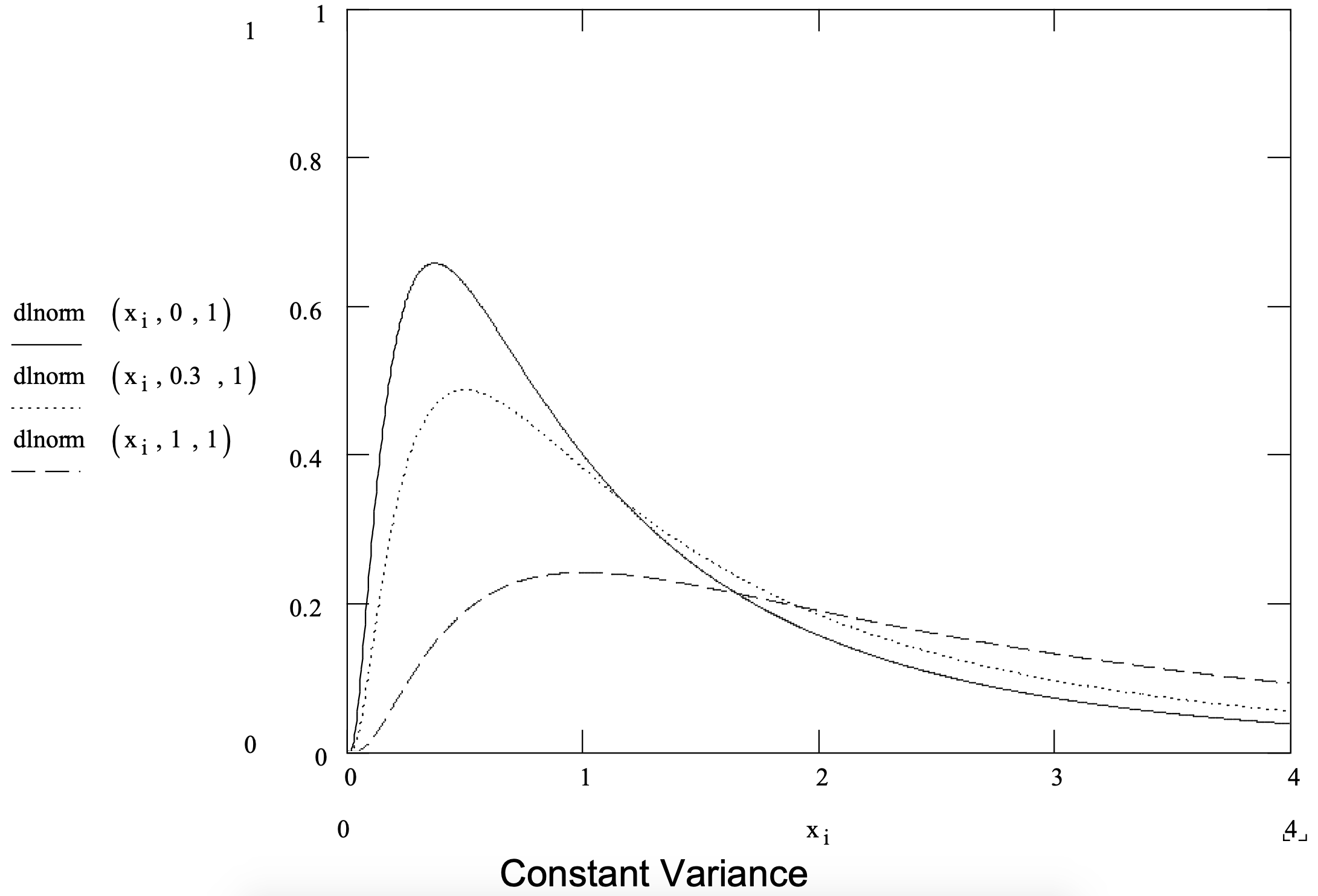
Parámetros:	media (\(\ \mu\)) y desviación estándar (\(\ \sigma\)) de la distribución normal que resulta de tomar el logaritmo natural de la distribución logarítmica normal
Rango:	[0,\(\ \infty\))
Media:	\(\ e^{\mu+o^{2} / 2}\)
Varianza:	\(\ e^{2 \mu+o^{2}}\left(e^{o^{2}}-1\right)\)
Densityfunction:	\(\ f(x)=\frac{1}{x \sqrt{2 \pi o^{2}}} e^{\frac{-(\ln (x)-\mu)^{2}}{2 \sigma^{2}}} ; x>0\)
Función de distribución:	Sin forma cerrada
Aplicación:	La distribución lognormal se utiliza para modelar el tiempo entre fallas del equipo así como los tiempos de operación. Por los teoremas del límite central, la distribución lognormal se puede utilizar para modelar cantidades que son los productos de un gran número de otras cantidades.

La distribución gamma se resume en la Figura 3-8.

Figura 3-8: Resumen de la distribución gamma

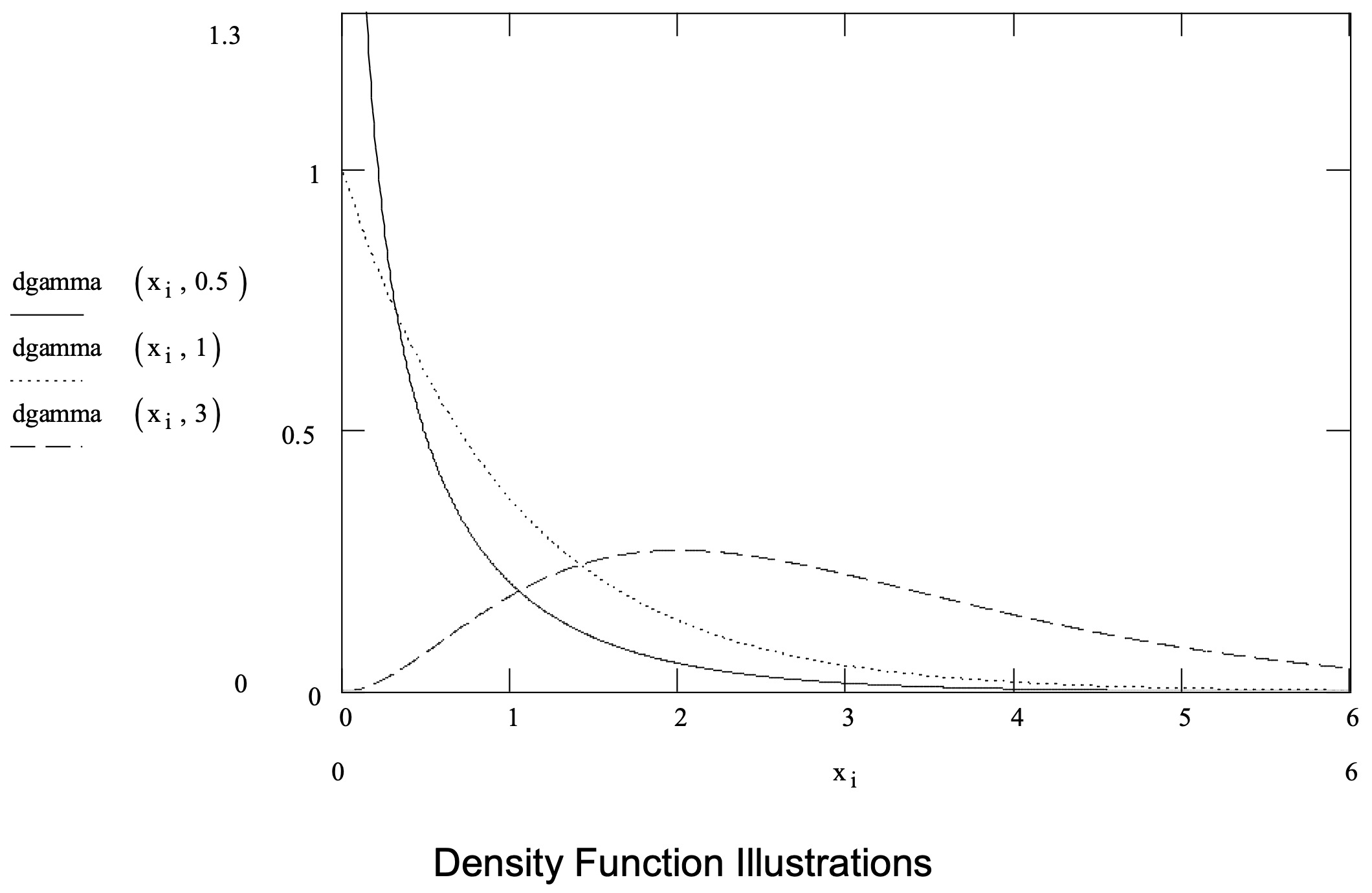
Parámetros:	Parámetro de forma,\(\ \alpha\) > 0, y un parámetro de escala,\(\ \beta\) > 0.
Rango:	[0,\(\ \infty\))
Media:	\(\ \alpha * \beta\)
Varianza:	\(\ \alpha * \beta^{2}\)
Función de densidad:	\(\ f(x)=\frac{\beta^{-\alpha} x^{\alpha-1} e^{-(x / \beta)}}{\Gamma(\alpha)} ; x>0\)
Función de distribución:	Sin forma cerrada, excepto cuando\(\ \alpha\) es un entero positivo.
Aplicación:	La distribución gamma es la distribución más flexible y general para modelar los tiempos de operación.

A menudo se argumenta que el experimento de simulación debe incluir la posibilidad de largos tiempos de operación, inspección y transporte. Un solo tiempo de este tipo puede tener un efecto notable en el funcionamiento del sistema ya que las siguientes entidades esperan los recursos ocupados. En este caso, se puede usar una distribución Weibull, lognormal o gamma, ya que cada una se extiende hasta el infinito positivo.

Un argumento contrario al uso de tiempos de retardo largos es que representan una variación de causa especial. A menudo, la variación de causa especial no se considera durante las fases iniciales del diseño del sistema y, por lo tanto, no se incluiría en el experimento de simulación. La fase de diseño a menudo considera solo la dinámica nominal del sistema.

Los controles se utilizan a menudo durante el funcionamiento del sistema para ajustarse a los tiempos de retardo largos. Por ejemplo, una pieza que requiere un tiempo de procesamiento prolongado puede estar fuera de especificación y descartarse después de que se realice una cantidad de procesamiento previamente especificada. Dichos controles se pueden incluir en modelos de simulación si se desea.

La distribución normal, en virtud de teoremas de límite central (Ley, 2007), es útil para representar cantidades que son la suma de un gran número (25 a 30 por lo menos) de otras cantidades. Por ejemplo, una región de ventas consta de 100 tiendas de conveniencia. La demanda de un producto en particular en esa región es la suma de las demandas en cada tienda. La demanda regional se modela como normalmente distribuida. Esta idea se ilustra en el estudio de aplicación sobre la gestión automatizada de inventarios.

Una sola operación se puede utilizar para modelar múltiples tareas. En este caso, el tiempo de operación representa la suma de los tiempos para realizar cada tarea. Si hay suficientes tareas involucradas, el tiempo de operación se puede modelar usando la distribución normal.

Los parámetros de una función de distribución normal son la media (\(\ \mu\)) y la desviación estándar (\(\ \sigma\)). La Figura 3-8 muestra varias funciones de densidad de distribución normal y resume la distribución normal.

Algunas cantidades tienen que ver con el número de algo, como el número de piezas en un lote, el número de artículos que un cliente exige del inventario o el número de clientes que llegan entre el mediodía y la 1:00 P.M. Dichas cantidades se pueden modelar utilizando la distribución de Poisson.

A diferencia de las distribuciones discutidas anteriormente, el rango de la distribución de Poisson es solo valores enteros no negativos. Así, el Poisson es una distribución discreta. El Poisson tiene sólo un parámetro, la media.

Tenga en cuenta que si la distribución de Poisson se utiliza para modelar el número de eventos en un intervalo de tiempo, como el número de clientes que llegan entre el mediodía y la 1:00 P.M., ese tiempo entre los eventos, llegadas, se distribuye exponencialmente. Además, la distribución normal puede ser utilizada como aproximación a la distribución de Poisson. La distribución de Poisson se resume en la Figura 3- 9.

Algunas cantidades pueden tomar uno de un pequeño número de valores, cada uno con una probabilidad dada. Por ejemplo, una parte es de tipo “1” con 70% de probabilidad y de tipo “2” con 30% de probabilidad. En estos casos, simplemente se enumera la función de masa de probabilidad, p. ej. p ₁ = 0.70 y p ₂ = 0.30. La función de masa de probabilidad enumerada se resume en la Figura 3-10.

Figura 3-8: Resumen de la Distribución Normal.

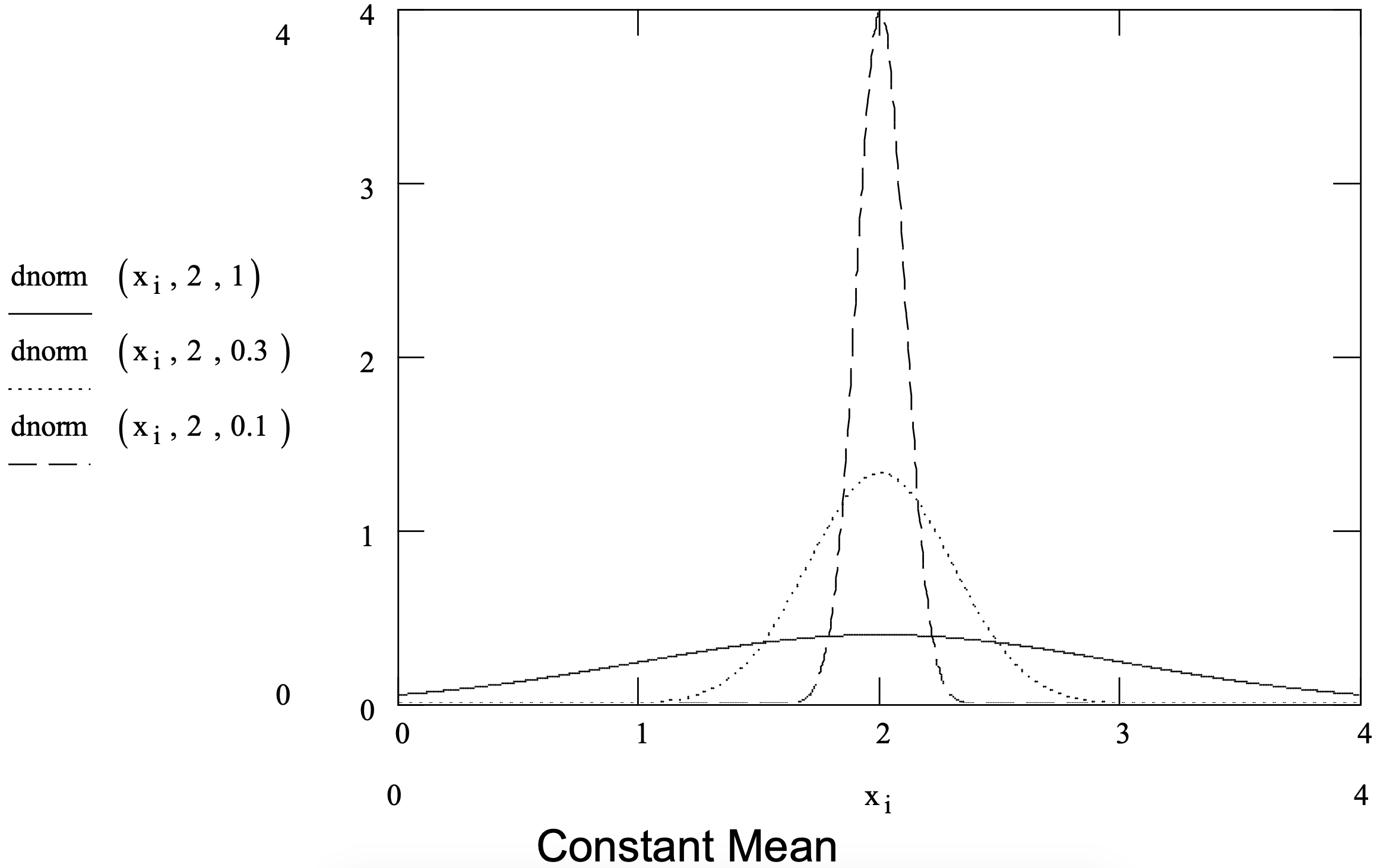
Parámetros:	media (\(\ \mu\)) y desviación estándar (\(\ \sigma\))
Rango:	(-\(\ \infty\),\(\ \infty\))
Media:	\(\ \mu\)
Varianza:	\(\ \sigma^{2}\)
Densityfunction:	\(\ f(x)=\frac{1}{\sqrt{2 \pi o^{2}}} e^{\frac{-(x-\mu)^{2}}{2 \sigma^{2}}}\)
Función de distribución:	Sin forma cerrada
Aplicación:	Por los teoremas del límite central, la distribución normal puede ser utilizada para modelar cantidades que son la suma de un gran número de otras cantidades.

Figura 3-9: Resumen de la distribución de Poisson

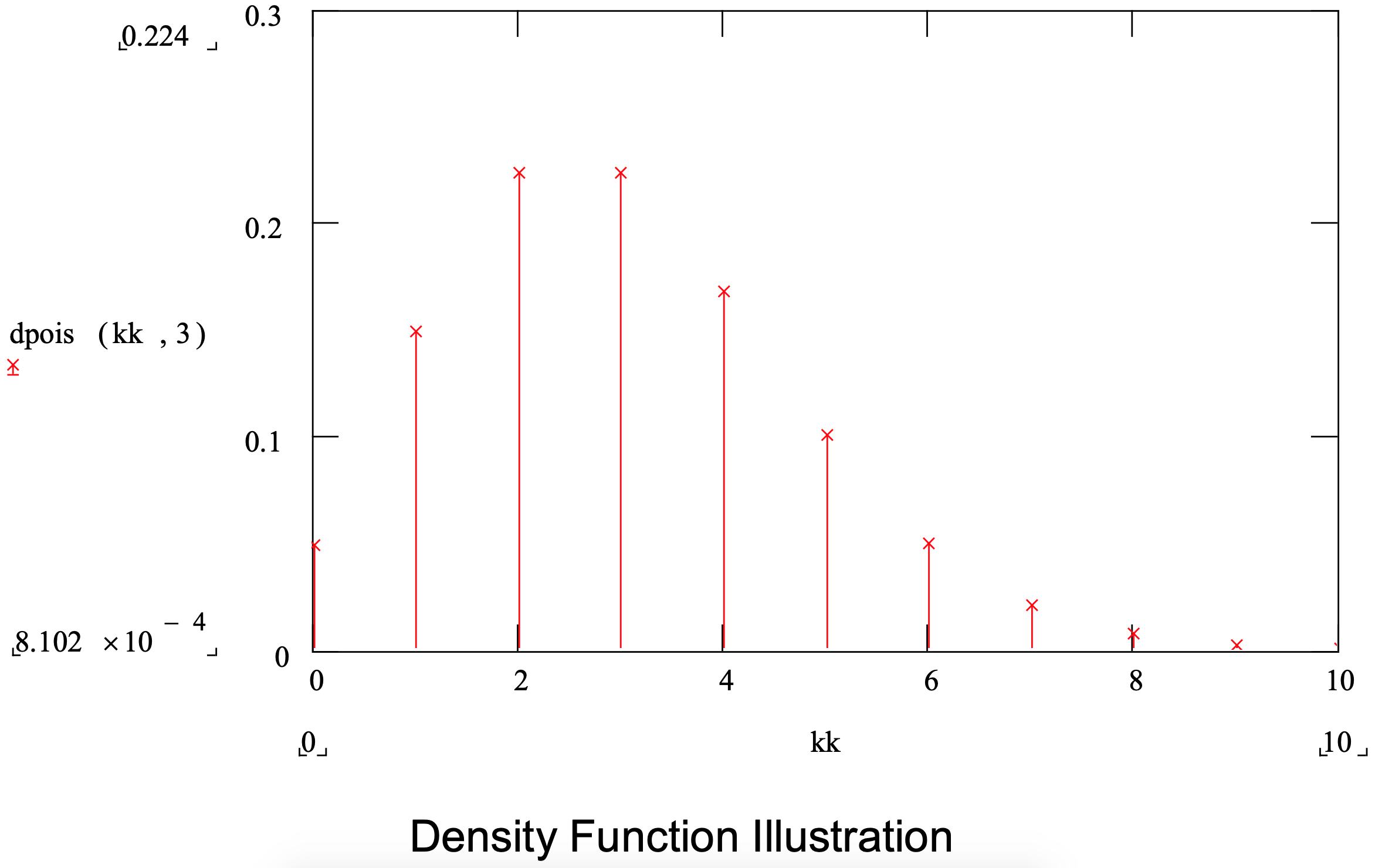
Parámetro:	media
Rango:	Números enteros no negativos
Media:	parámetro dado
Varianza:	media
Masa:	\(\ p(x)=\frac{e^{-\text {mean}} * \text {mean}^{x}}{\mathrm{x} !} ; x \text { is a non - negative integer }\)
Función de distribución:	\(\ F(x)=e^{-m e a n} * \sum_{i=0}^{x} \frac{m e a n^{i}}{i !} ; x \text { is a non - negative integer }\)
Aplicación:	La distribución de Poisson se utiliza para modelar cantidades que representan el número de cosas como el número de artículos en un lote, el número de artículos demandados por un solo cliente o el número de llegadas en un cierto período de tiempo.

Figura 3-10: Resumen de la Función de Masa de Probabilidad Enumerada

Parámetro:	conjunto de pares valor-probabilidad (x,, pi), número de pares, n
Rango:	[mínimo x i, máximo x i]
Media:	\(\ \sum_{i=1}^{n} p_{i} * x_{i}\)
Varianza:	\(\ \sum_{i=1}^{n} p_{i} *\left(x_{i}-\text { mean }\right)^{2}\)
Función de masa:	\(\ p\left(x_{i}\right)=p_{i}\)
Función de distribución:	\(\ F\left(x_{i}\right)=\sum_{k=1}^{i} p_{k}\)
Aplicación:	Una función de masa de probabilidad enumerada se utiliza para modelar cantidades que representan el número de cosas como el número de artículos en un lote y el número de artículos demandados por un solo cliente donde se conoce la probabilidad de cada número de artículos y el número de valores posibles es pequeño.

Law y McComas (1996) estiman que “quizás un tercio de todos los conjuntos de datos no están bien representados por una distribución estándar”. En este caso, existen dos opciones:

1. Formar una función de distribución empírica a partir del conjunto de datos.
2. Ajustar una forma funcional generalizada al conjunto de datos que tiene la capacidad de representar un número ilimitado de formas.

El primero se puede lograr usando el histograma de frecuencia de un conjunto de datos para modelar una cantidad aleatoria. Las desventajas de este enfoque son que la simulación considera solo valores dentro del rango del conjunto de datos y en proporción a las celdas que componen el histograma.

Una forma de lograr esto último es ajustando una función Bezier al conjunto de datos usando un programa informático interactivo basado en Windows como lo describen Flannigan Wagner y Wilson (1995, 1996).

3.3.3 Un enfoque basado en software para ajustar un conjunto de datos a una función de distribución

En esta sección se analiza el uso de software informático para ajustar una función de distribución a los datos. Siempre se debe usar software para este propósito y varios paquetes de software respaldan esta tarea. Es necesario realizar las siguientes tres actividades.

1. Selección de la familia de distribución o familias de interés.
2. Estimar los parámetros de distribuciones particulares.
3. Determinar qué tan bien se ajusta cada distribución a los datos.

Las funciones de distribución discutidas en las secciones anteriores, beta o normal por ejemplo, se denominan familias. Una distribución individual se especifica estimando valores para sus parámetros. Hay dos posibilidades para seleccionar una o más familias de funciones de distribución como candidatas para modelar una cantidad aleatoria.

1. Realizar la selección a partir de la correspondencia entre la situación que se modela y las propiedades teóricas de la familia de distribución tal y como se presenta en los apartados anteriores.

   Por ejemplo, un cliente grande compra un producto en particular a un proveedor. El cliente abastece numerosas tiendas de cada compra. El tiempo entre compras es una variable aleatoria. Con base en las propiedades teóricas de las distribuciones previamente discutidas, el tiempo entre pedidos podría modelarse usando una distribución exponencial y el número de unidades de producto comprado podría modelarse usando una distribución normal.

2. Realizar la selección en función de la correspondencia entre estadísticas de resumen y gráficas, como un histograma, y funciones de densidad particulares. Paquetes de software como ExpertFit [Law y McComas 1996, 2001] computan y comparan automáticamente, utilizando una medida relativa de ajuste, distribuciones de probabilidad de candidatos y sus parámetros. En ExpertFit, la medida relativa del ajuste se basa en un algoritmo patentado que incluye métodos estadísticos y heurísticos.

   Por ejemplo, se recogen 100 observaciones de un tiempo de operación. A partir de estos datos se construye un histograma. Se computan la media y la desviación estándar. La Figura 3-11 muestra el histograma en la misma gráfica que una distribución logarítmica normal y una distribución gamma cuya media y desviación estándar se estimaron a partir del conjunto de datos. Tenga en cuenta que la distribución gamma (línea discontinua) parece ajustarse a los datos mucho mejor que la distribución lognormal (línea punteada).

Figura 3-11: Comparación de un Histograma con Funciones de Densidad Gamma y Lognormal

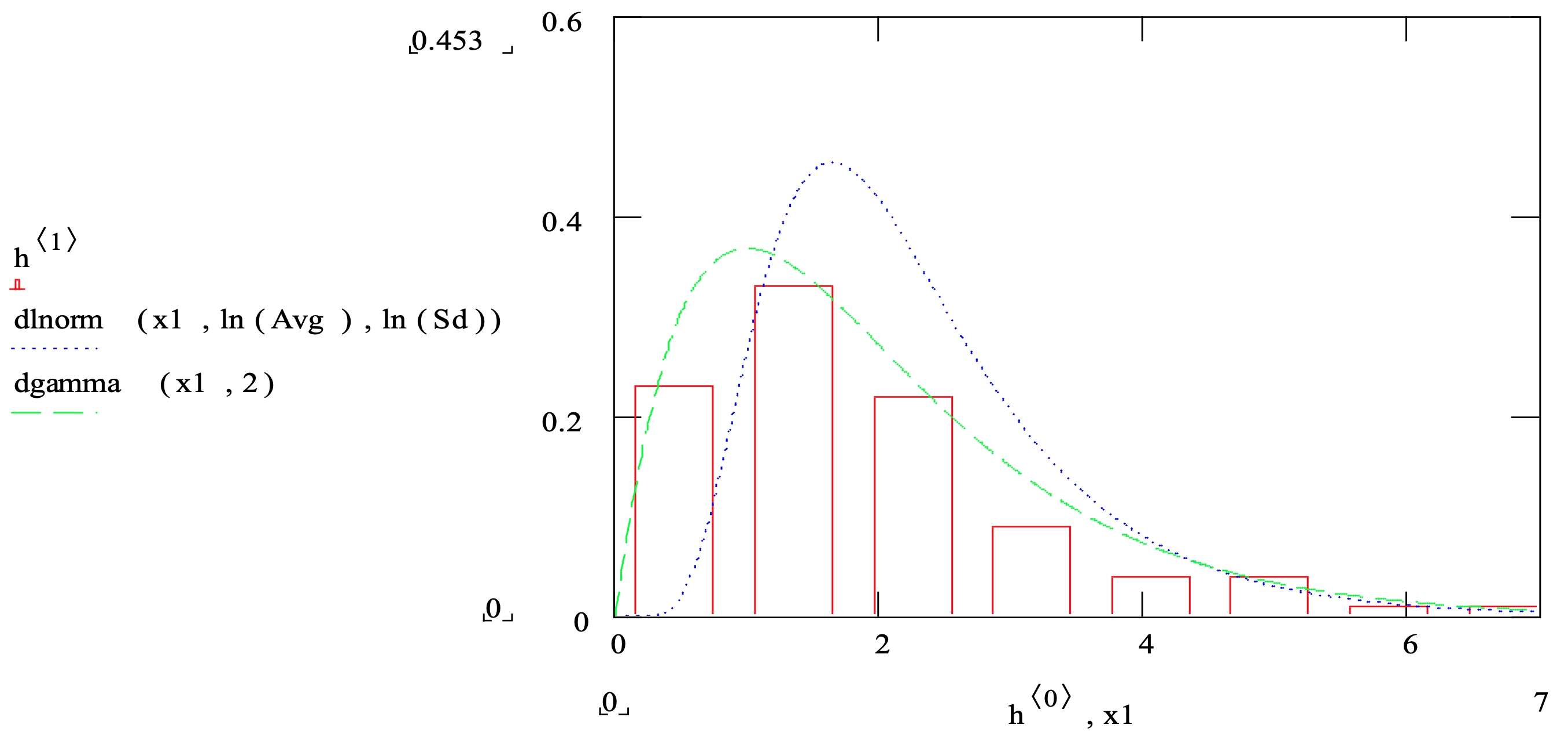
Para algunas distribuciones, la estimación de los valores de los parámetros es sencilla. Por ejemplo, los parámetros de la distribución normal son la media y la desviación estándar que se estiman por la media muestral y la desviación estándar de la muestra calculada a partir de los datos disponibles. Para otras distribuciones, la estimación de parámetros es compleja y puede requerir métodos estadísticos avanzados. Por ejemplo, ver la discusión del procedimiento de estimación para los parámetros de distribución gamma en Ley (2007). Afortunadamente, estos métodos se implementan en el software de ajuste de funciones de distribución.

La tercera actividad consiste en evaluar qué tan bien cada distribución de candidatos representa los datos y luego elegir la distribución que mejor se ajuste. A esto se le llama determinar la “bondad de ajuste”. El modelador utiliza pruebas estadísticas que evalúan la bondad de ajuste, las medidas heurísticas relativas y absolutas de ajuste, y el juicio subjetivo basado en pantallas gráficas interactivas para seleccionar una distribución entre varios candidatos.

Los procedimientos heurísticos incluyen los siguientes:

1. Densidad/histograma sobre gráficas — Trazar el histograma del conjunto de datos y una función de distribución candidata en la misma gráfica que en la Figura 3-11. Comprobar visualmente la correspondencia de la función de densidad con el histograma.
2. Comparaciones de frecuencia — Compara el histograma de frecuencia de los datos con la probabilidad calculada a partir de la distribución candidata de estar en cada celda del histograma.

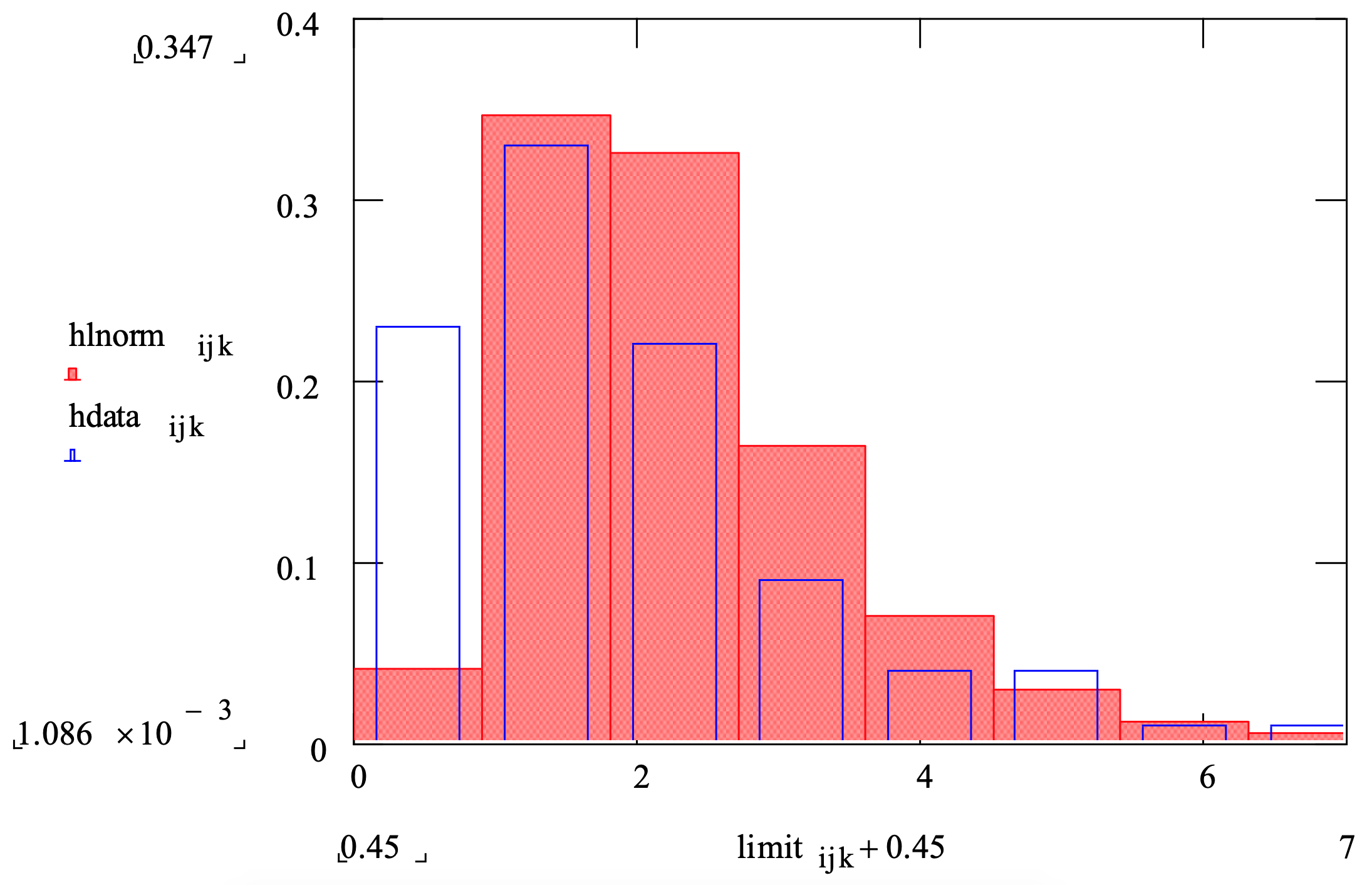
   Por ejemplo, la Figura 3-12 muestra una gráfica de comparación de frecuencias que muestra el conjunto de datos de muestra cuyo histograma se muestra en la Figura 3-11 así como la distribución lognormal cuya media y desviación estándar se estimaron a partir del conjunto de datos. Las diferencias entre la distribución logarítmica normal (barras sólidas) y el conjunto de datos (barras no sólidas) se ven fácilmente.

   Figura 3-12: Comparación de frecuencia de un conjunto de datos con una distribución lognormal

   

3. Gráficas de diferencia de función de distribución — Trazar la diferencia de la distribución candidata acumulativa y la fracción de valores de datos que son menores que x para cada valor del eje x en la gráfica. Cuanto más cerca esté la trama rastrea la línea 0 en el eje vertical, mejor.

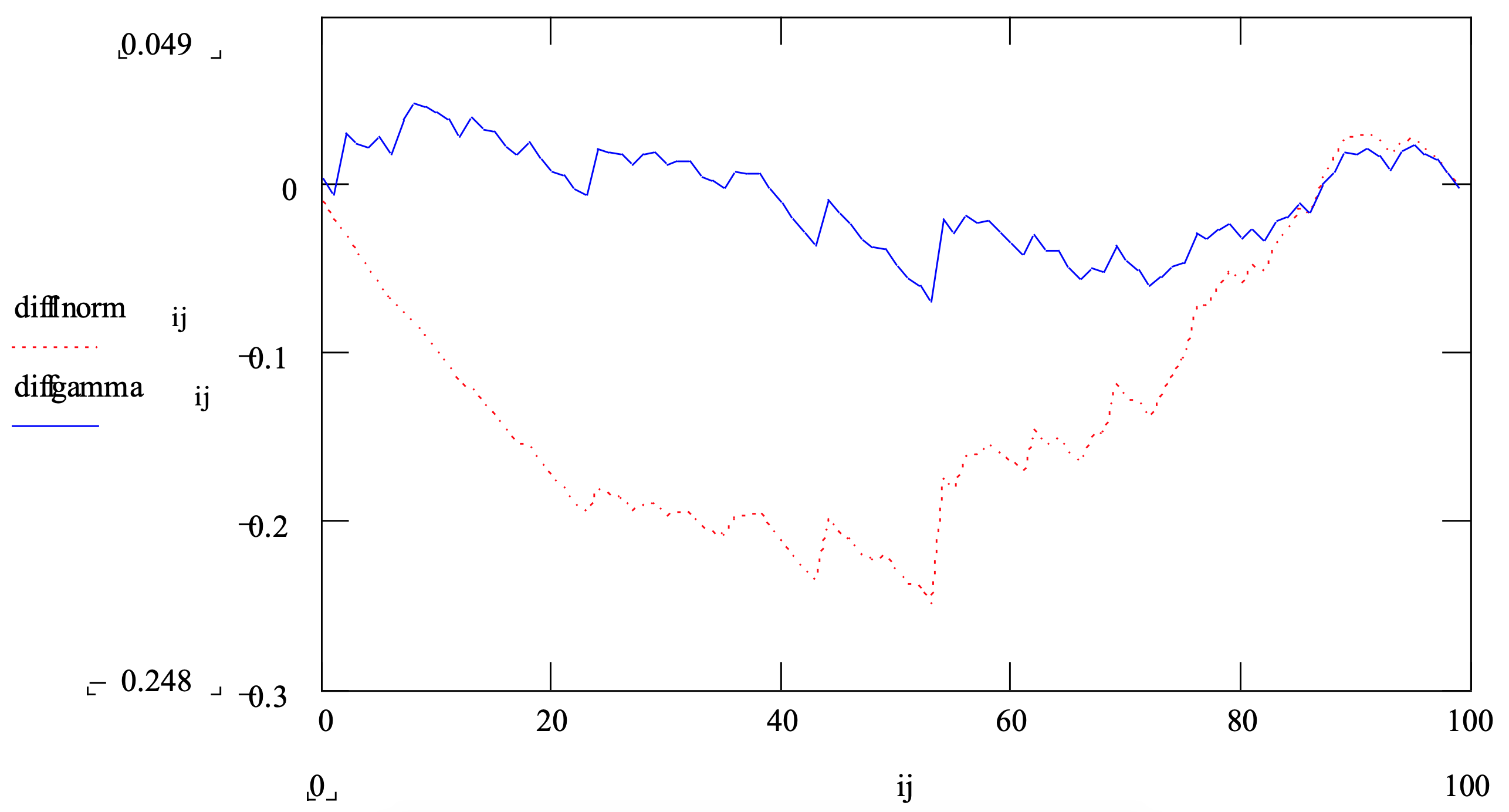
   Por ejemplo, la Figura 3-13 muestra una gráfica de diferencias de función de distribución comparando el conjunto de datos de muestra cuyo histograma se muestra en la Figura 3-11 con las distribuciones gamma y lognormales cuyas desviaciones medias y estándar se estimaron a partir de los datos. La distribución gamma (línea continua) parece ajustarse al conjunto de datos mucho más estrechamente que la distribución lognormal (línea punteada).

   Figura 3-13: Comparación de Gráfica de Diferencia de Función de Distribución de un Conjunto de Datos con una Distribución Gamma y una Distribución Lognormal

   

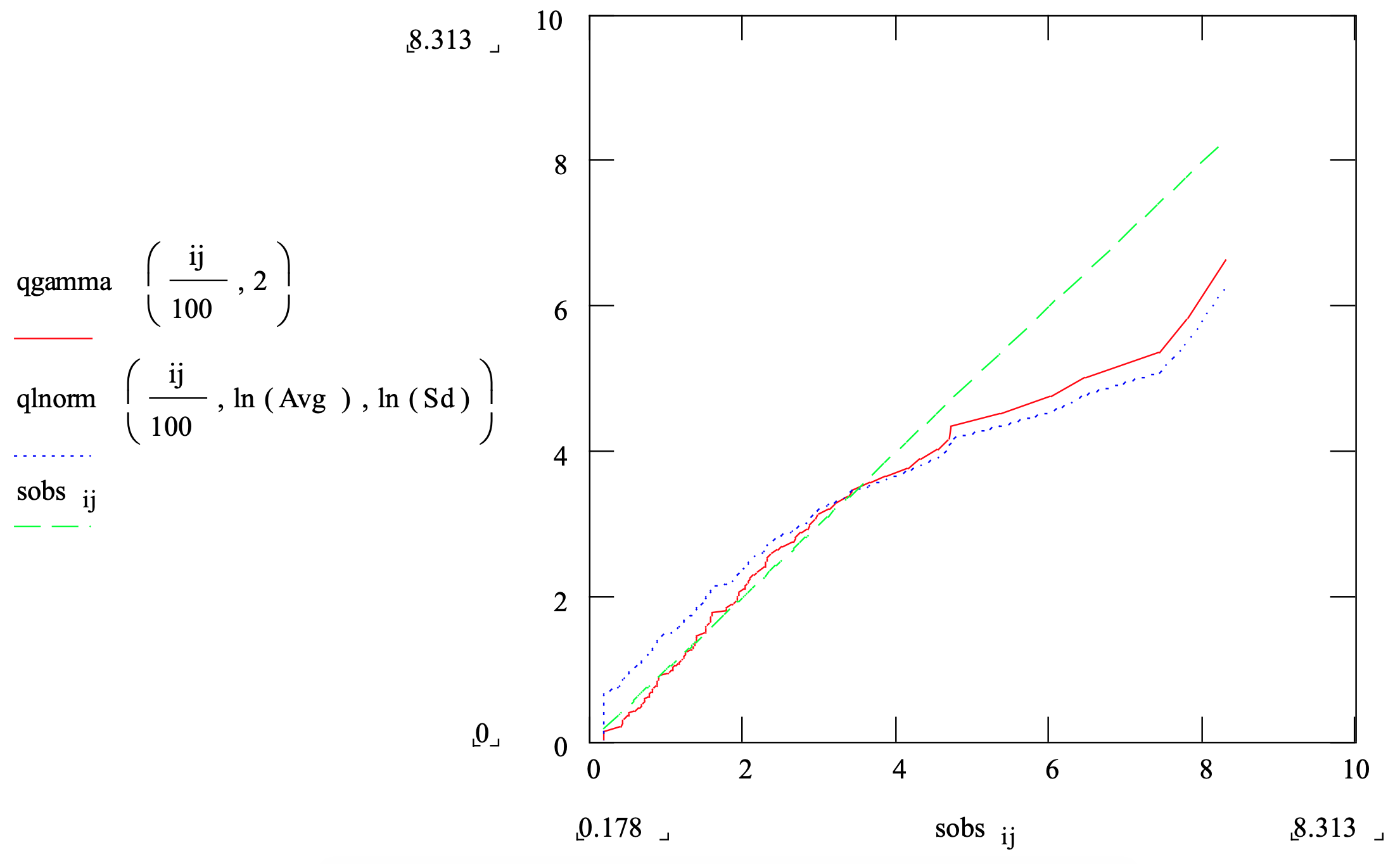
4. Gráficas de probabilidad — Utilice uno de los muchos tipos de gráficas de probabilidad para comparar el conjunto de datos y la distribución de candidatos. Uno de esos tipos es el siguiente. Supongamos que hay n valores en el conjunto de datos. Se trazan los siguientes puntos, n en número: (i/n º punto porcentual de la distribución candidata, el i-ésimo valor más pequeño en el conjunto de datos). Estos puntos cuando se trazan deben seguir una línea de 45 grados. Cualquier desviación sustancial de esta línea indica que la distribución de candidatos puede no ajustarse al conjunto de datos.

   Por ejemplo, la Figura 3-14 muestra una gráfica de probabilidad que compara el conjunto de datos de muestra cuyo histograma se muestra en la Figura 3-11 con las distribuciones gamma y lognormales mostradas en la misma figura. Tenga en cuenta que la distribución gamma (línea continua) rastrea la línea de 45 grados mejor que la distribución lognormal (línea punteada) y ambas se desvían de la línea más hacia la cola derecha.

   Figura 3-14: Comparación de Gráfica de Probabilidad de un Conjunto de Datos con Distribuciones Gamma y Lognormales

   

Las pruebas estadísticas evalúan formalmente si el conjunto de datos que consiste en muestras independientes es consistente con una distribución de candidatos. Estas pruebas proporcionan un enfoque sistemático para detectar diferencias relativamente grandes entre un conjunto de datos y una distribución de candidatos. Si no se encuentran tales diferencias, lo mejor que se puede decir es que no hay evidencia de que la distribución de candidatos no se ajuste al conjunto de datos.

El comportamiento de estas pruebas depende del número de valores en el conjunto de datos. Para valores grandes de n, las pruebas parecen detectar siempre una diferencia significativa entre una distribución de candidatos y un conjunto de datos. Para valores menores de n, las pruebas detectan solo diferencias brutas. Esto debe tenerse en cuenta a la hora de interpretar los resultados de la prueba.

Las siguientes pruebas son comunes y generalmente se realizan mediante software de ajuste de función de distribución.

1. Prueba de Chi-cuadrado — compara formalmente un histograma del conjunto de datos con una distribución de candidatos tal como se hizo visualmente usando una gráfica de comparación de frecuencias.
2. Prueba de Kolmogorov-Smironv (K-S) — compara formalmente una función de distribución empírica construida a partir del conjunto de datos con una distribución acumulativa candidata, que es análoga a la gráfica de diferencia de función de distribución.
3. Prueba de Anderson-Darling: compara formalmente una función de distribución empírica construida a partir del conjunto de datos con una función de distribución acumulativa candidata, pero es mejor para detectar diferencias en las colas de la distribución que la prueba K-S.

En este capítulo se discute cómo determinar la función de distribución a utilizar en el modelado de una cantidad aleatoria. Se ha ilustrado cómo esta elección puede afectar los resultados de un estudio de simulación. Se han discutido algunas cuestiones relacionadas con la obtención y el uso de datos. Se ha presentado la selección de una distribución tanto utilizando un conjunto de datos como en ausencia de datos.

Problemas

1. Enumere las distribuciones que tienen un límite inferior.
2. Enumere las distribuciones que tienen un límite superior.
3. Enumere las distribuciones que son continuas.
4. Enumere las distribuciones que son discretas.
5. Supongamos que X es una variable aleatoria que sigue una distribución beta con rango [0,1]. Se necesita una variable aleatoria, Y, que siga una distribución beta con rango [10, 100]. Dar una ecuación para Y en función de X.
6. Supongamos que los datos no están disponibles cuando se inicia un proyecto de simulación.
   1. ¿Qué tres parámetros se estiman comúnmente sin datos?
   2. Se especifica un tiempo de operación dando sólo dos parámetros: mínimo y máximo. Sin embargo, se va a modelar utilizando una distribución triangular. ¿Qué harías?
7. Considera el siguiente conjunto de datos: 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 15, 16, 17, 17, 18, 18, 18, 20, 20, 21, 21, 24, 27, 29, 30, 37, 40, 40. ¿Qué familia de distribución parece encajar mejor con los datos? Usa estadísticas resumidas y un histograma para ayudarte.
8. Hipótesis de una o más familias de distribuciones para cada uno de los siguientes casos:
   1. Tiempo entre clientes que llegan a un restaurante de comida rápida durante la hora de la cena vespertina.
   2. El tiempo hasta el siguiente fallo de una máquina cuya tasa de fallas es constante.
   3. El tiempo hasta el siguiente fallo de una máquina cuya tasa de fallas aumenta en el tiempo.
   4. El tiempo de carga manual de un camión basado en el diseño operativo de un sistema.

      Usted pide a los diseñadores del sistema los tiempos mínimos, promedio y máximos.

   5. El tiempo para realizar una tarea con tiempos de tarea largos posible.
   6. La distribución de los tipos de trabajo en una tienda.
   7. El número de artículos que exige cada cliente.
9. ¿Qué familia de funciones de distribución parece ajustarse mejor al siguiente conjunto de datos? Usa estadísticas resumidas y un histograma para ayudarte. Pruebe su selección utilizando las parcelas comentadas en la sección 3.3.2.

   8.39	3.49	3.17	15.34	4.68	4.38	0.02	1.21
   3.56	0.50	4.38	2.53	20.61	2.78	2.66	32.88
   22.49	5.10	4.58	3.07	22.64	34.86	9.59	0.67
   12.24	3.25	34.07	5.43	14.72	5.84	15.37	21.20
   0.21	3.20	25.12	3.18	3.60	11.45	1.07	8.69
   0.46	9.16	10.71	3.75	1.54	0.65	3.68	10.46
   20.11	5.81	4.63	3.13	8.99	2.82	0.87	13.45
   10.10	12.57	22.67	3.55	5.68	29.07	0.62	25.23
   17.97	35.76	17.05	4.61	12.36	14.02	24.33	11.05
   1.10	4.56	9.51	7.31	23.33	5.81	3.48	3.23

10. ¿Qué familia de funciones de distribución parece ajustarse mejor al siguiente conjunto de datos? Usa estadísticas resumidas y un histograma para ayudarte. Pruebe su selección utilizando las parcelas comentadas en la sección 3.3.2.

    2373	2361	2390	2377	2333
    2327	2380	2373	2360	2382

11. Utilice el software de ajuste de funciones de distribución para resolver los problemas 7, 9 y 10.