6.3: El estudio de caso

El estudio de caso muestra el proceso de uso conjunto de modelos de simulación y análisis para abordar problemas relacionados con una nueva estación de trabajo antes de su adquisición e implementación.

6.3.1 Definir los problemas y el objetivo de la solución

Un equipo lean ha estado estudiando el funcionamiento de una estación de trabajo en particular. Una máquina de reemplazo con menor variación en el tiempo de procesamiento, pero el mismo tiempo promedio de procesamiento, se ha propuesto como parte de una definición de estado futuro. La administración requiere un estudio para determinar los tiempos promedio y máximos de entrega en la estación de trabajo si se adquiere la máquina de reemplazo.

La estación de trabajo opera 168 horas al mes. La demanda de los clientes por mes es de 1680 piezas o 10 partes por hora, lo que resulta en un tiempo de toma de 6 minutos. El tiempo de procesamiento para la nueva máquina se distribuye triangularmente con una media de 5 minutos, un mínimo de 3 minutos y un máximo de 8 minutos. Así, el modo es de 4 minutos. (Véase la discusión en el capítulo 3 para el cómputo de la modalidad.) La llegada entrante de piezas no está bien controlada, lo que se modelará utilizando el peor de los casos prácticos: Distribuido exponencialmente con una media igual al tiempo takt de 6 minutos.

6.3.2 Construir modelos

A continuación se muestra el modelo en pseudo-inglés.

---

Definir llegadas: \(\ \quad\quad\)Hora de la primera llegada: \(\ \quad\quad\)Tiempo entre llegadas: \(\ \quad\quad\)Número de llegadas:	//la media debe ser igual al tiempo takt 0 Distribuido exponencialmente con una media de 6 minutos Exponencial (6) minutos Infinito//Nota: El número promedio de llegadas es de 1680
Definir recursos: \(\ \quad\quad\)WS/1 con estados (Ocupado, Inactiva)
Definir atributos de entidad: \(\ \quad\quad\)ArrivalTime	//parte etiquetada con su hora de llegada; cada parte tiene su propia etiqueta
Estación de trabajo de proceso
Comenzar \(\ \quad\quad\)Establecer ArrivalTime = Reloj \(\ \quad\quad\)Espere hasta que WS/1 esté inactivo en la cola QWS \(\ \quad\quad\)Hacer que WS/1 esté ocupado \(\ \quad\quad\)Espere a Triangular (3, 4, 8) minutos \(\ \quad\quad\)Hacer que WS/1 esté inactivo \(\ \quad\quad\)Tabular (Clock-ArrivalTime) en LeadTime Fin	//parte de tiempo récord llega en la etiqueta //parte espera su giro en la máquina //parte comienza a encender la máquina; la máquina está ocupada //parte es procesada //la pieza está terminada; la máquina está inactiva //realizar un seguimiento del tiempo parcial en la máquina

---

Las definiciones hablan sobre las llegadas, la máquina incluyendo sus estados, y los atributos de entidad (parte). Los comentarios (denotados por//) describen los pasos por los que pasa la pieza para su procesamiento en la máquina así como registrar la hora de llegada y tabular su tiempo de entrega individual justo antes de la salida.

6.3.3 Identificar causas raíz y evaluar alternativas iniciales

En esta sección se presenta el diseño experimental de simulación y los resultados. En primer lugar, en la siguiente sección se discute un modelo analítico de la estación de trabajo única.

6.3.3.1 Modelo analítico de una sola estación de trabajo

_{El tiempo entre llegadas se caracteriza tanto por una media, T a, como por una desviación estándar,\(\ \sigma_a\) y el tiempo de procesamiento se caracteriza tanto por su TC media como por su desviación estándar,\(\ \sigma_T\).} El coeficiente de variación del tiempo entre llegadas es\(\ \mathrm{c}_{\mathrm{a}}=\sigma_{\mathrm{a}} / \mathrm{T}_{\mathrm{a}}\). El coeficiente de variación del tiempo de procesamiento es\(\ \mathrm{c}_{\mathrm{T}}=\sigma_{\mathrm{T}} / \mathrm{C} \mathrm{T}\).

El número promedio de piezas en el búfer es WIP _q y WIP _q más la utilización de la máquina (igual al número promedio de piezas en procesamiento) es el WIP.

El tiempo promedio que se pasa en la estación de trabajo puede dividirse en dos partes: el tiempo promedio en el procesamiento, CT, y el tiempo promedio en el búfer, CT _q. Su suma es el total es el tiempo de espera LT.

La relación entre WIP, tiempo de entrega y rendimiento se conoce como Ley de Little.

\(\ \begin{align}Work in process (WIP) = Throughput (TH) X Lead Time (LT)\tag{6-1}\end{align}\)

Ejemplos:

Número de piezas en una estación de trabajo =	Piezas terminadas por hora en la estación de trabajo X Tiempo total en la estación de trabajo
Número de clientes en Burger King =	Clientes atendidos por hora en Burger King X Tiempo desde la entrada hasta la finalización del servicio en BK
Número de tarimas en un transportador de sujeción =	Tarimas que ingresan al transportador de línea principal por hora X Tiempo hasta la entrada al transportador de retención hasta la entrada al transportador de línea principal
Número de unidades en un centro de transferencia =	Número de unidades que ingresan al centro de transferencia por hora X Tiempo promedio de procesamiento en el centro de transferencia
Número de alumnos matriculados en GVSU =	Número de alumnos que ingresan por año X Promedio de años matriculados en GVSU

1. Para que el WIP (algo malo tener muchos) disminuya, el rendimiento debe disminuir (para un tiempo de entrega constante) o el tiempo de ciclo debe disminuir para un rendimiento constante. Dado que el rendimiento a menudo depende de los requisitos para los productos terminados y es el recíproco del tiempo de toma, lo más probable es que sea necesario disminuir el tiempo de entrega para disminuir el WIP.
2. Otra forma de escribir la Ley de Little es TH = WIP/LT. Esto significa que el aumento del rendimiento se puede lograr aumentando WIP o disminuyendo la LT. Sin embargo, aumentar el WIP (es malo tener muchos) puede aumentar el tiempo de entrega. Por lo tanto, aumentar el rendimiento con mayor frecuencia requiere disminuir el tiempo de entrega. Tenga en cuenta que se puede lograr el mismo rendimiento con WIP grandes y plazos de entrega grandes o WIP pequeños y plazos de entrega pequeños.
3. Una tercera forma de escribir la Ley de Little es LT = WIP/TH. La disminución de LT se puede lograr disminuyendo el WIP o aumentando el rendimiento si el WIP no aumenta.

A continuación consideraremos toda la información que se pueda calcular sobre el comportamiento de una sola estación de trabajo que tenga una máquina o un trabajador. Incluiremos medias y varianzas en la evaluación del comportamiento promedio. Observe que la variación en las medidas de comportamiento no es, y muchas veces no puede, determinarse analíticamente.

Considere la estación de trabajo que se muestra en la Figura 6-1, con las cantidades calculadas mostradas en negritas. Las cantidades que se conocen son el tiempo entre llegadas (media y varianza) así como el tiempo de procesamiento (media y varianza). Las cantidades que se pueden calcular son:

1. tiempo en el búfer de entrada de la estación (CT _q)
2. tiempo de entrega en la estación (LT)
3. número promedio de piezas en el búfer de entrada (WIP _q)
4. número promedio de refacciones en la estación (WIP)
5. utilización de la estación, el porcentaje de tiempo que la estación de trabajo está ocupada procesando una pieza. \(\ (\mu)\)
6. tiempo entre salidas (media y desviación estándar) (T _d y\(\ \sigma\) _d)

Figura 6-1: Computación de Cantidades de Estación de Trabajo

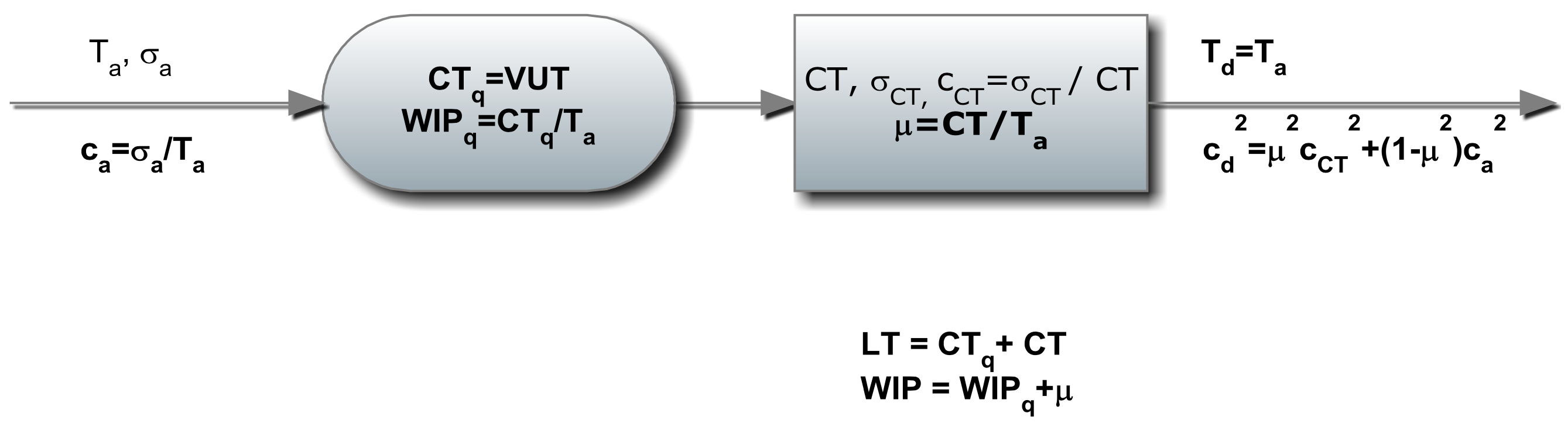
La ecuación 6-2 se llama la ecuación VUT, para Varianza — Utilización — Tiempo y se utiliza para aproximar el tiempo promedio del ciclo en la cola. Esta ecuación se presenta y se discute más a fondo en Hopp y Spearman (2007).

\ begin {align} C T_ {q}\ approx V U T=\ izquierda (\ frac {c_ {a} ^ {2} +c_ {C T} ^ {2}} {2}\ derecha)\ izquierda (\ frac {\ mu} {1-\ mu}\ derecha) C T\ tag {6-2}\ end {align}

Los siguientes conocimientos se pueden obtener examinando la ecuación 6-2.

1. El tiempo de ciclo en el búfer depende de la varianza del tiempo entre llegadas y la varianza del tiempo de procesamiento, expresada como el coeficiente de variación cuadrado. A medida que aumenta la varianza de cualquiera, aumenta el tiempo promedio de ciclo en la cola. El coeficiente de variación es la desviación estándar/media.
2. El tiempo de ciclo en el búfer aumenta de una manera altamente no lineal a medida que aumenta la utilización. El término de utilización para una utilización del 90% es 9, para una utilización del 95% es 19, y para una utilización del 99% es 99.
3. La única manera de ejecutar eficazmente una estación de trabajo con alta utilización es eliminar la variación en el tiempo entre las llegadas y el tiempo de procesamiento.
4. No se puede lograr una utilización del 100% a menos que la varianza tanto en el tiempo de procesamiento como en el tiempo entre llegadas sea cero.
5. La media y la desviación estándar de la distribución exponencial son iguales. Así, el coeficiente de variación para una distribución exponencial es igual a 1. Así, el rango “bueno” para el término V es de 0 a 1.
6. No se requieren las distribuciones del tiempo entre llegadas y los tiempos de procesamiento, solo la media y la desviación estándar.

Una vez que se determina el tiempo promedio del ciclo en el búfer, el número promedio en el búfer se puede determinar usando la Ley de Little:

\ begin {align} W I P_ {q} =C T_ {q} *\ frac {1} {T_ {a}}\ tag {6-3}\ end {align}

El tiempo de entrega en la estación es simplemente el tiempo de ciclo en el búfer más el tiempo de procesamiento:

\ begin {align} L T=C T_ {q} +T\ tag {6-4}\ end {align}

El número en la estación se puede obtener de la ecuación 6-4 usando la Ley de Little:

\ begin {align} W I P=L T *\ frac {1} {T_ {a}} =\ izquierda (C T_ {q} +T\ derecha) *\ frac {1} {T_ {a}} =W I P_ {q} +\ mu\ tag {6-5}\ end {align}

La media del tiempo entre salidas debe ser igual a la media del tiempo entre llegadas. Esto es simplemente una ley de conservación de las partes: Todas las partes que entren deben partir. También se aplica la ley de conservación entre estaciones de trabajo: La media y variación del tiempo entre salidas de una estación de trabajo son las mismas que la media y variación del tiempo entre llegadas a la siguiente estación de trabajo.

El coeficiente cuadrado de determinación del tiempo entre salidas viene dado por la ecuación 6-6:

\ begin {align} c_ {d} ^ {2} =u^ {2} c_ {T} ^ {2} +\ izquierda (1-u^ {2}\ derecha) c_ {a} ^ {2}\ tag {6-6}\ end {align}

Los siguientes conocimientos se pueden obtener examinando la ecuación 6-6.

1. La variación en las salidas para una estación de trabajo de alta utilización depende principalmente de la variación en el tiempo de procesamiento. Por lo tanto, un tiempo de procesamiento de baja variación da como resultado una baja variación en las salidas, lo que resulta en una baja variación en las llegadas a la siguiente estación de trabajo.
2. Una estación de trabajo con alta utilización y baja variación en el tiempo de procesamiento eliminará, en gran medida, una gran variación en el tiempo entre llegadas.
3. Una estación de trabajo con alta utilización y alta variación en el tiempo de procesamiento causará una gran variación en el tiempo entre las llegadas a la siguiente estación. Así, el tiempo de ciclo en el búfer en la siguiente estación tenderá a ser alto.
4. Una estación de trabajo con baja utilización tenderá a dar como resultado la variación del tiempo entre llegadas a la siguiente estación de trabajo, igualando la variación en el tiempo entre salidas en la estación de trabajo actual.

Los resultados del modelo analítico de la estación de trabajo de interés se muestran en la Tabla 6-1.

Tabla 6-1: Modelo analítico de estación de trabajo — Resultados
Insumos	Tiempo promedio entre llegadas	6
	Tiempo promedio de procesamiento	5
	Std. Tiempo de desarrollo entre llegadas	6
	Std. Tiempo de procesamiento de Dev.	3
Utilización	Utilización	83.3%
Tiempos promedio	c a — Tiempo entre llegadas	1
	c T — Tiempo de procesamiento	0.6
	Término de varianza	0.68
	Término de utilización	5.0
	Tiempo promedio en búfer	17.0
	Promedio de tiempo de entrega	22.0
Número promedio de piezas	Número promedio en el búfer	2.8
	Número promedio en la estación	3.7
Información de Salida	Tiempo promedio entre salidas	6
	c d ^2 — Tiempo entre salidas	0.56

Obsérvese que las entradas al análisis son el promedio y la desviación estándar del tiempo entre llegadas así como la media y desviación estándar del tiempo de procesamiento. Los promedios se obtienen típicamente a través de mapeo de flujo de valores. Las desviaciones estándar generalmente deben obtenerse a través de la recolección y análisis de datos adicionales.

6.3.3.2 Análisis de simulación de la estación de trabajo única

A continuación, se debe especificar el diseño para el experimento de simulación. Este diseño hará uso de los resultados del modelo analítico.

El diseño experimental contiene los elementos discutidos en el capítulo 4. Se trata de una simulación de terminación de duración 168 horas, el periodo de planeación mensual. Se requieren dos corrientes, una para el tiempo entre llegadas y otra para el tiempo de procesamiento. Las condiciones iniciales se establecen en base a los resultados del modelo analítico: 2 partes en el buffer y así una parte adicional en la máquina. El tiempo de entrega es la principal medida de desempeño de interés. Algunas de las otras cantidades calculadas por el modelo analítico también son de interés: utilización de la máquina y número promedio de piezas en el búfer. Estos serán utilizados en la obtención de evidencias de validación para el modelo de simulación y experimento. Se realizarán veinte repeticiones. No hay parámetros del modelo en el primer experimento.

En resumen, el diseño del experimento es el siguiente:

Cuadro 6-2: Diseño del Primer Experimento de Simulación para la Estación de Trabajo.
Elemento del experimento	Valores para este experimento
Tipo de experimento	Terminando
Parámetros del modelo y sus valores	Ninguno
Flujos de números aleatorios	Tiempo entre llegadas Tiempo de operación
Medidas de desempeño	Plazo de entrega parcial Utilización de la máquina Número de piezas que esperan la máquina en el búfer
Número de réplicas	20
Condiciones Iniciales	2 partes en el búfer, lo que implica una parte en la máquina
Intervalo de tiempo simulado (Hora de inicio — hora de finalización)	0 — 168 horas

La evidencia de verificación se obtiene usando la ecuación de saldo:

Número de entidades que ingresan = Número de entidades que salen + Número de entidades que quedan al final

El número de entidades que ingresan al modelo es la suma de las que llegan y las entidades iniciales.

Así, para la primera réplica:

1717 + 3 = 1719 + 1.

Así, se obtiene evidencia de validación.

En el Cuadro 6-3 se muestran los resultados de la simulación. Estos resultados son consistentes con los resultados del modelo analítico. Los intervalos de confianza del 99% para la utilización, el número promedio de piezas que esperan en la estación y el tiempo promedio de entrega contienen los valores correspondientes resultantes del modelo analítico. Así, se obtiene evidencia de validación del modelo.

Tabla 6-3: Resultados de simulación para el experimento base
Replicar	Número promedio en la estación	Tiempo de entrega promedio	Tiempo de entrega máximo	Utilización
1	3.20	18.80	74.70	0.86
2	2.99	18.11	79.15	0.83
3	3.40	20.36	83.38	0.83
4	3.70	21.15	61.29	0.88
5	2.28	14.13	54.11	0.80
6	2.76	16.79	61.17	0.82
7	3.39	20.17	75.93	0.84
8	2.57	15.66	60.89	0.82
9	3.17	18.52	79.15	0.86
10	3.36	20.34	97.58	0.83
11	2.92	16.99	60.50	0.86
12	4.51	26.07	104.61	0.87
13	3.11	18.97	81.80	0.82
14	2.63	16.46	67.19	0.80
15	3.23	18.89	75.20	0.86
16	2.75	16.62	90.52	0.82
17	2.56	15.49	62.29	0.83
18	2.53	15.66	68.35	0.80
19	5.52	31.55	138.89	0.88
20	4.45	25.75	129.22	0.87
Promedio	3.25	19.32	80.30	0.84
Std. Dev.	0.79	4.24	22.63	0.02
99% CI Límite Inferior	2.74	16.61	65.82	0.82
Límite superior del 99% CI	3.76	22.03	94.77	0.85

6.3.4 Revisar y ampliar el trabajo anterior

La gerencia revisó el modelo de simulación y el experimento, concluyendo que el modelo fue validado como una herramienta para evaluar el estado futuro antes de su implementación.

Los resultados del tiempo de entrega de los modelos fueron motivo de preocupación con respecto a cómo operaría la estación de trabajo. El tiempo promedio de entrega fue aproximadamente cuatro veces el tiempo de procesamiento. El tiempo de entrega máximo promedio estimado por el modelo de simulación fue de aproximadamente 16 veces el tiempo de procesamiento. Estos valores altos se deben en su totalidad a la variación en la llegada de las partes u órdenes entrantes (expresadas modelando el tiempo entre llegadas como distribuidos exponencialmente) así como a la variación en el tiempo de procesamiento como se ve en el coeficiente de variación de 0.60. Por lo tanto, reducir esta variación al identificar y abordar las causas raíz parece fundamental para hacer que la operación de la estación de trabajo sea más ágil.

En la reunión de revisión, se solicitó evaluar los efectos de tres detractores en el desempeño de las estaciones de trabajo. La valoración de cada uno debía hacerse independientemente de los demás.

La naturaleza de estos detractores se discute en la siguiente sección.

6.3.4.1 Desempeño de detractores al puesto de trabajo

El primer detractor son las averías. Las averías reducen la cantidad de tiempo de producción disponible. Un período de operación para una sola máquina termina en una avería. La duración de este periodo es muy variable. Se necesita algún tiempo para reparar la máquina, lo que podría variar según el tipo de avería. Este ciclo de reparación de averías se repite como se muestra en la Figura 6-2.

Figura 6-2: Ciclo de Operación y Reparación

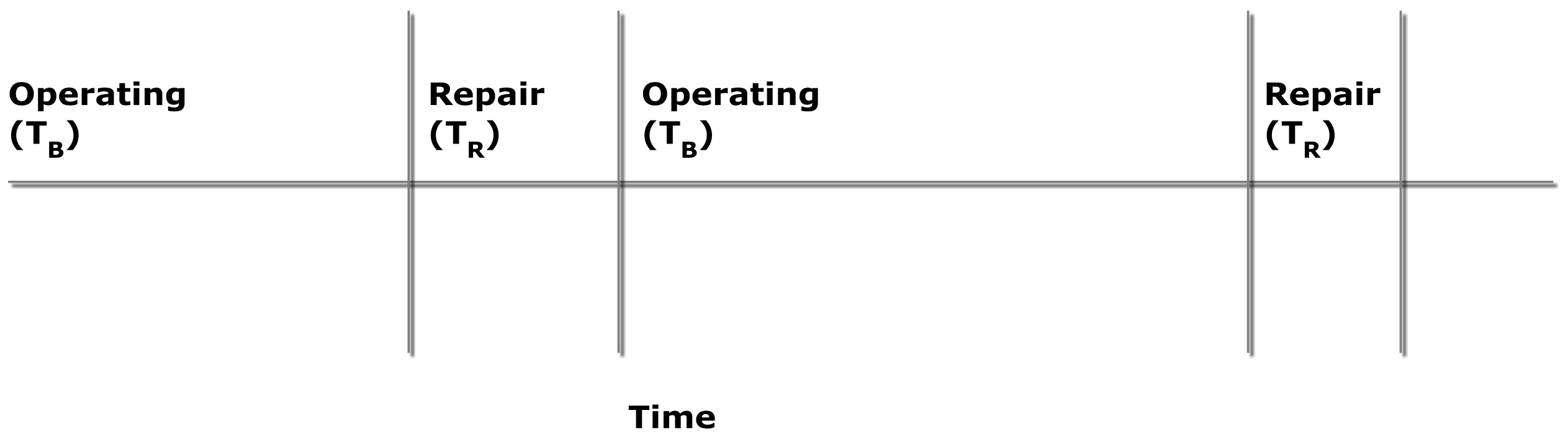
Que T _B denota el tiempo promedio entre el final de una reparación y la siguiente avería y T _R denota el tiempo promedio de reparación. Entonces la cantidad T _B + T _R es la duración en tiempo del ciclo de reparación de averías. La disponibilidad se define como el porcentaje de tiempo que la máquina no se rompe y se calcula de la siguiente manera.

\ begin {align} A=\ frac {T_ {B}} {T_ {B} +T_ {R}}\ tag {6-7}\ end {align}

En cuanto a la disponibilidad, cabe señalar lo siguiente:

1. El tiempo para completar todo el trabajo (operaciones en piezas) se reduce a A% del tiempo original.
2. El tiempo de entrega de las piezas que esperan la estación de trabajo mientras se está reparando será mucho más largo que para las piezas que no esperan una reparación. De esta manera, se incrementará el promedio, máximo y desviación estándar del plazo de entrega.

En este caso, la máquina se descompone en promedio una vez por semana (40 horas) y tarda entre 30 minutos y 2 horas en repararse. Dado que el tiempo entre averías es altamente variable, se modela como distribuido exponencialmente con una media de 40 horas. El tiempo de reparación se modela como uniformemente distribuido entre 30 minutos y 2 horas (120 minutos).

El segundo detractor son piezas defectuosas. O bien es necesario fabricar piezas adicionales o las piezas defectuosas deben ser reelaboradas para satisfacer la demanda. Esto aumenta la cantidad de trabajo que se necesita hacer para producir el número de piezas necesarias para satisfacer la demanda. Si es necesario hacer piezas adicionales o el tiempo promedio de reelaboración es el mismo que el tiempo promedio de producción, el número de piezas que se necesitan hacer viene dado por la ecuación 6-8 donde p es el porcentaje de piezas que están defectuosas.

\ begin {align}\ mathrm {D} _ _ {\ mathrm {Nuevo}} =\ mathrm {D} _ {\ mathrm {Antiguo}}/(1-\ mathrm {p})\ tag {6-8}\ end {align}

Cabe señalar lo siguiente con respecto a las piezas defectuosas.

1. El incremento en el trabajo incrementará la utilización de la estación de trabajo, lo que a su vez incrementa el tiempo de entrega como se muestra en la ecuación VUT (6-2).
2. Efectivamente, hay más llegadas a la estación de trabajo lo que disminuye el tiempo entre llegadas a TBA * (1-p).

En el caso, dejar p = 5%.

El detractor final se configura y el procesamiento por lotes resultante de las piezas. El proceso de configuración y procesamiento por lotes es el siguiente. A medida que llegan, las partes se reúnen en un grupo llamado lote hasta que el número de partes en el grupo sea igual al tamaño de lote predeterminado (b). El lote recién formado ingresa al búfer de la máquina para esperar el procesamiento. Procesar el lote significa realizar una operación de configuración en la máquina y luego procesar todos los artículos del lote.

Debe tenerse en cuenta lo siguiente con respecto a la configuración y el procesamiento por lotes.

1. Esperar a que se forme un lote aumentará el promedio, el máximo y la desviación estándar del tiempo de entrega.
2. Debe ser cierto lo siguiente: b*takt time >= setup time + b * tiempo de operación
3. El tamaño mínimo de lote factible puede ser mayor a uno, dado el ítem anterior en la lista.

Esto lleva a la siguiente pregunta: ¿Cuál es el valor más pequeño del tamaño del lote de tal manera que la utilización, que ahora incluye el tiempo de configuración, está lo más cerca posible de un valor dado? Disminuir el tamaño del lote aumenta el número de configuraciones y, por lo tanto, la cantidad de tiempo dedicado a realizar el trabajo de configuración, lo que no es productivo. Sin embargo, la disminución del tamaño del lote disminuye el trabajo en proceso y los inventarios de productos terminados y respalda un programa de producción más flexible. Estos objetivos son consistentes con el logro de un entorno de producción lean.

La utilización debe calcularse como se muestra en la ecuación 6-9.

\ begin {align}\ mu=\ left (\ text {hora de configuración} +\ mathrm {b} ^ {*}\ mathrm {CT}\ derecha)/\ izquierda (\ mathrm {b} ^ {*}\ mathrm {T} _ {\ mathrm {a}}\ derecha)\ tag {6-9}\ end {align}

Entonces el tamaño de lote más pequeño para un valor dado de la utilización viene dado por la ecuación 6-9a.

\ begin {align} b=\ operatorname {setup}\ operatorname {time}/\ left (u * T_ {a} -C T\ right)\ tag {6-9a}\ end {align}

Este problema también se puede formular y resolver utilizando una hoja de cálculo para facilitar la evaluación de valores alternativos del tamaño del lote. Estas alternativas podrían incluir cumplir con restricciones como el tamaño del lote debe ser un múltiplo de 10. La evaluación se realiza calculando la utilización y el número de lotes en función del tamaño de lote seleccionado.

Se ingresa la utilización objetivo. Se minimiza la desviación absoluta entre la utilización real y el objetivo. En otras palabras, el tamaño del lote n se cambia hasta que la utilización real esté lo más cerca posible del objetivo. Esto se puede hacer manualmente o con una de las herramientas de hoja de cálculo: solver y búsqueda de objetivos. Nota: si se usa la búsqueda de objetivos, comience con un tamaño de lote muy pequeño.

En este caso, la utilización objetivo se establece en 95% y el tiempo de configuración es de 30 minutos. En el Cuadro 6-4 se muestra cómo se determinó un tamaño de lote de 42. Obsérvese que el valor del tamaño del lote calculado usando la ecuación 6-9a es 42.9.

Tabla 6-4: Resultado de la búsqueda de un tamaño de lote objetivo
Insumos	Utilización de objetivos	95%
	Tiempo promedio entre llegadas	6
	CT	5
	Tiempo de configuración	30
	Demanda	1680
Resultado	Tamaño del lote (b)	42
Cómputos	Numerador	240
	denominador	252
	Utilización	95.2%
	Desviación	0.2%
	Número de Lotes	40