6.8: Ejemplo de Modelado y Controlador PID - Control de Crucero para un Vehículo Eléctrico

Introducción

Los principios de controles desarrollados en este curso pueden ser aplicados a sistemas de ingeniería no química como los automóviles. Algunas compañías, como NAVTEQ, están desarrollando productos de control de crucero adaptativo que utilizan información sobre el terreno próximo para cambiar de marcha de una manera más inteligente, lo que mejora la regulación de velocidad y el ahorro de combustible. Este estudio de caso examinará los fundamentos de desarrollar un controlador de velocidad para un vehículo eléctrico.

Se eligió un vehículo eléctrico por las siguientes razones:

• Los vehículos eléctricos son interesantes desde una perspectiva de ingeniería y pueden convertirse en una realidad para los consumidores en el futuro
• El par producido por un motor eléctrico es instantáneo (para todos los fines prácticos). De esta manera se puede ignorar el retraso del actuador, simplificando el desarrollo de dicho controlador.
• Algunos vehículos eléctricos cuentan con motores directamente integrados en el buje de las ruedas motrices. Esto elimina la necesidad de una transmisión y simplifica los modelos de dinámica del vehículo.

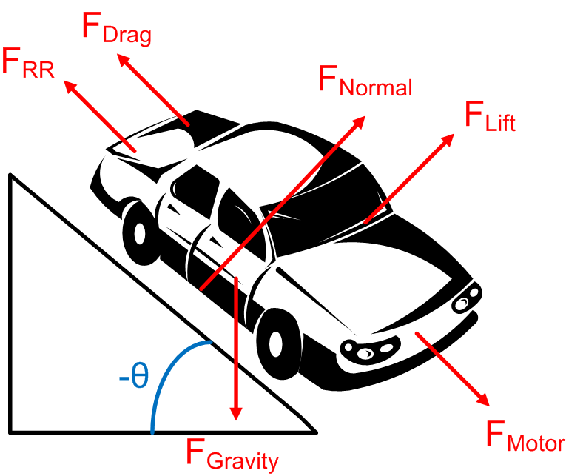
Fuerzas

Como se muestra en el diagrama de carrocería libre a continuación, hay seis fuerzas que actúan sobre el vehículo:

1. Resistencia a la rodadura
2. Arrastre aerodinámico
3. Elevación aerodinámica
4. Gravedad
5. Normal
6. Motor

Figura 1: Un diagrama de cuerpo libre de las fuerzas que actúan sobre el vehículo. \(-\theta\)se utiliza para denotar el grado de la carretera de tal manera que un valor positivo de\(\theta\) corresponde al vehículo que viaja cuesta arriba.

Resistencia a la rodadura

La resistencia a la rodadura se debe a que las llantas se deforman al entrar en contacto con la superficie de una carretera y varía según la superficie sobre la que se conduce. Puede ser modelo usando la siguiente ecuación:

\[F_{R R}=C_{r r 1} v+C_{r r 2} F_{N} \nonumber \]

Las dos constantes de resistencia a la rodadura se pueden determinar experimentalmente y pueden ser proporcionadas por la fabricación de neumáticos. 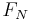es la fuerza normal.

Arrastre aerodinámico

El arrastre aerodinámico es causado por la pérdida de impulso de las partículas de aire a medida que fluyen sobre el capó del vehículo. La resistencia aerodinámica de un vehículo se puede modelar usando la siguiente ecuación:

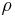• es la densidad del aire. A 20°C y 101kPa, la densidad del aire es de 1.2041 kg/m ³.
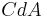• es el coeficiente de arrastre para el vehículo multiplicado por el área de referencia. Los valores típicos para automóviles se enumeran aquí.
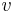• es la velocidad del vehículo.

Elevación aerodinámica

La elevación aerodinámica es causada por la diferencia de presión entre el techo y la parte inferior del vehículo. La elevación se puede modelar usando la siguiente ecuación:

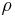• es la densidad del aire. A 20°C y 101kPa, la densidad del aire es de 1.2041 kg/m ³.
• es el coeficiente de elevación del vehículo multiplicado por el área de referencia.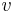
• es la velocidad del vehículo.

Gravedad

En el diagrama anterior, hay un componente de gravedad tanto en la dimensión normal a la carretera como en la dimensión en la que viaja el vehículo. Usando trigonometría simple, el componente en la dimensión de recorrido se puede calcular de la siguiente manera:

\[F_{G, t r a v e l}=m g \sin (-\theta) \nonumber \]

• \(m\)es la masa del vehículo.
• \(g\)es la aceleración debida a la gravedad.

Fuerza Normal

La fuerza normal es la fuerza extraída por la carretera sobre las llantas del vehículo. Debido a que el vehículo no se mueve hacia arriba o hacia abajo (relativo a la carretera), la magnitud de las fuerzas normales es igual a la magnitud de la fuerza debido a la gravedad en la dirección normal a la carretera.

• \(m\)es la masa del vehículo.
• \(g\)es la aceleración debida a la gravedad.

Motor

El par producido por un motor eléctrico es aproximadamente proporcional a la corriente que fluye a través del stater del motor. En este caso de estudio, se controlará la corriente aplicada al motor para regular la velocidad. Aplicar una corriente negativa hará que el vehículo frene regenerativamente.

\[ \tau=k_{\text {motor}} I \nonumber \]

\[F_{M}=\frac{\tau}{r}=\frac{k_{\text {motor }} I}{r} \nonumber \]

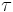• es el par producido por el motor.
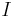• es la corriente que fluye a través del motor.
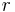• es el radio de la llanta.
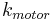• es una constante.

Segunda Ley de Newton

Usando la Segunda Ley de Newton, se puede obtener un diferencial para la velocidad del vehículo.

\[\begin{align*} m a &=\sum F \\[4pt] &=F_{M}-F_{d r a g}-F_{R R}+F_{G, \text {travel}} \end{align*} \nonumber \]

Sustituir en las expresiones diversas fuerzas detalladas anteriormente arroja lo siguiente:

Al sustituir adicionalmente la expresión por fuerzas normales se obtiene lo siguiente:

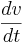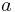Sustituyendo los resultados en lo siguiente:

Agrupar como giros da como resultado lo siguiente:

Para simplemente el análisis restante, se definen varias constantes de la siguiente manera:

\[\beta=r C_{r r 1} \nonumber \]

\[\gamma=r C_{r r 2} m g \cos (-\theta)-r m g \sin (-\theta) \nonumber \]

Sustituyendo estos en la ecuación diferencial da como resultado la siguiente expresión:

\[\frac{d v}{d t}=\frac{\tau-\alpha v^{2}-\beta v-\gamma(\theta)}{m r} \nonumber \]

Es importante que\(\theta\) (y por lo tanto también\(\gamma\)) sea una función de la posición del vehículo.

Controlador PID

Una forma de regular la velocidad del vehículo es controlar el par generado por el motor eléctrico. Si el par motor es mayor que el par resistivo que actúa sobre el vehículo (una suma de arrastre aerodinámico, resistencia a la rodadura, etc.), el vehículo acelerará. Si el par motor es menor que el par resistivo, el vehículo disminuirá la velocidad.

Expresión para corriente de fase

Para un motor eléctrico, la corriente de fase que fluye a través del motor es proporcional al par producido. Por lo tanto, una estrategia para controlar la velocidad de los vehículos es controlar la corriente de fase del motor.

Usando una arquitectura de controlador PID, la expresión para la corriente del motor es la siguiente:

\[I=K_{c}\left(v_{s e t}-v\right)+\frac{1}{\tau_{I}} \int(v-v_{set}) d t+\tau_{D} \frac{d\left(v_{s e t}-v\right)}{d t}+C_{offset} \nonumber \]

Ecuación diferencial para velocidad

Sustituir esta expresión en la ecuación diferencial para la posición del vehículo da como resultado lo siguiente:

\[\dfrac{dv}{dt} = \frac{k_{motor}[K_{c}(v_{set}-v) + \frac{1}{\tau_{I}} \int {(v_{set}-v)dt} + \tau_{D} \frac{d(v_{set}-v)}{dt} + C_{offset}]- \alpha v^2 - \beta v - \gamma(\theta)}{m r} \nonumber \]

Definir otra variable\(x_1\) permite la eliminación de la integral de la expresión.

\[\frac{d x_{1}}{d t}=v_{s e t}-v \nonumber \]

\[\frac{d v}{d t}=\frac{k_{\text {motor}}\left[K_{c}\left(v_{\text {isct }}-v\right)+\frac{x_{1}}{\tau_{l}}+\tau_{D} \frac{d\left(v_{a=t}-v\right)}{d t}+ C_{offset} \right]-\alpha v^{2}-\beta v-\gamma(\theta).}{m r} \nonumber \]

Si todos los cambios en\(v_{set}\) son graduales entonces\(\frac{d v_{set}}{d t} \approx 0\). La aplicación de esta simplificación da como resultado la siguiente expresión:

\[\frac{d v}{d t}=\frac{k_{\text {motor }}\left[K_{c}\left(v_{\text {set }}-v\right)+\frac{x_{1}}{\tau_{1}}-\tau_{D} \frac{d v}{d t}+C_{\text {offset }}\right]-\alpha v^{2}-\beta v-\gamma(\theta)}{m r} \nonumber \]

Usando un poco de álgebra, se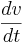 puede obtener una expresión for de la siguiente manera:

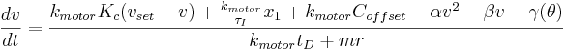
\[\frac{d v}{d t}=\frac{k_{\text {motor}} K_{c}\left(v_{\text {set}}^{k_{\text {motor}}} x_{1} | k_{\text {motor}} C_{\text {cffses}}^{2}\right)^{\alpha}(\theta)}{\dot{k}_{\text {motor}} l_{L}+mr} \nonumber \]

Encuentra Punto Fijo

El punto fijo se puede obtener estableciendo las derivadas a cero y resolviendo el sistema de ecuación.

Sistema de Ecuaciones:

\[\frac{d v}{d t}=\frac{k_{\text {meclor }} K_{c}\left(v_{\text {sel }}-v\right)+\frac{k_{\text {motor }}}{\tau_{I}} x_{1}+k_{\text {melur }} C_{v \int j s \leq \iota}-\alpha v^{2}-\beta v-\gamma(\theta)}{k_{\text {motor }} t_{D}+m r}=0 \nonumber \]

\[\frac{x_{1}}{d t}=v_{s e t}-v=0 \nonumber \]

Solución

\[x_{1}=\frac{\left.-\tau_{I}\left(k_{\text {motor}} C_{\text {offset}}-\alpha v_{\text {set}}^{2}-\beta v_{\text {set}}-\gamma(\theta)\right]\right)}{k_{\text {motor}}} \nonumber \]

\[v=v_{s e t} \nonumber \]

Como se esperaba, existe un punto fijo cuando la velocidad establecida es igual a la velocidad real del vehículo.

Linealizar Sistema de ODEs

Antes de que se pueda examinar (fácilmente) la estabilidad del sistema, el sistema debe linealizarse alrededor de un punto fijo.

Nota: Para simplemente las expresiones matriciales en sección se utilizará la siguiente notación:

\[y_{i}^{\prime}=\frac{d y_{i}}{d t} \nonumber \]

En general, un sistema linealizado de ODEs tiene la siguiente forma:

\ [\ left [\ begin {array} {c}
y_ {1} ^ {\ prime}\\
y_ {2} ^ {\ prime}\
\ vdots\\
y_ {n} ^ {\ prime}
\ end {array}\ derecha] =\ mathbf {J}\ left [\ begin {array} {c}
y_ {1}\\
y_ {2}\
\ vpuntos\\
y_ {n}
\ end {array}\ derecha] +\ left [\ begin {array} {c}
k_ {1}\\
k_ {2}\\
\ vdots\\
k_ {n}
\ end {array}\ derecha]\ nonumber\]

El primer paso de linealizar cualquier sistema de ODEs para calcular el jacobiano. Para este sistema en particular, el jacobiano puede calcularse de la siguiente manera:

\ [\ mathbf {J} =\ left [\ begin {array} {cc}
\ frac {\ parcial v^ {\ prime}} {\ parcial v} &\ frac {\ parcial v^ {\ prime}} {\ parcial x_ {1}}\
\ frac {\ parcial x_ {1} ^ {\ prime}} {\ parcial v} &\ frac {\ parcial x_ {1} ^ {\ prime}} {\ parcial x_ {1}}
\ end {array}\ derecha] =\ izquierda [\ begin {array} {cc}
\ frac {-k_ {m o t o r} K_ {c} -m r [2\ alfa v+\ beta]} {m r+k_ {m o t o r}\ tau_ {D}} &\ frac {k_ {\ texto {motor}}} {t_ {l}\ izquierda (m r+k_ {\ texto {motor}}\ tau_ {D}\ derecha)}\\
-1 & 0
\ end {array}\ derecha]\ nonumber\]

Luego se evalúa al jacobiano en el punto fijo:

\ [\ mathbf {J} =\ left [\ begin {array} {cc}
\ frac {-k_ {\ text {motor}} K_ {c} -m r\ left [2\ alpha v_ {\ text {set}} +\ beta\ derecha]} {m r+k_ {\ text {motor}}\ tau_ {D}} &\ frac {k_ {\ texto {motor}}} {t_ {I}\ izquierda (m r+k_ {\ text {motor}}\ tau_ {D}\ derecha)}\\
-1 y 0
\ end {array}\ derecha]\ nonumber\]

El siguiente paso si para calcular el vector de constantes. Para este sistema en particular, dicho vector puede calcularse de la siguiente manera:

\ [\ left [\ begin {array} {c}
k_ {v}\\
k_ {x_ {1}}
\ end {array}\ right] =\ left [\ begin {array} {c}
\ frac {\ left. -\ izquierda (-k_ {\ texto {motor}} K_ {c} -2\ alfa v_ {s e t} -\ beta\ derecha]\ derecha) v_ {s e t}} {\ izquierda (m r+k_ {\ texto {motor}}\ tau_ {D}\ derecha)} +\ frac {\ izquierda. \ left (k_ {\ text {motor}} C_ {\ text {offset}} -\ alpha v_ {\ text {set}} ^ {2} -\ beta v_ {\ text {set}} -\ gamma (\ theta)\ derecha]\ derecha)} {\ izquierda (m r+k_ {\ text {motor}}\ tau_ {D}\ derecha)}\\
v_ {\ text {set}}
\ end {array}\ derecha]\ nonumber\]

Combinando el jacobiano y el vector de constantes da como resultado el siguiente sistema linealizado:

\ [\ left [\ begin {array} {l}
v^ {\ prime}\\
x_ {1} ^ {\ prime}
\ end {array}\ right] =\ mathbf {J}\ left [\ begin {array} {l}
v\\
x_ {1}
\ end {array}\ right] +\ left [\ begin {array} {l}
k_ {v}\\
k_ {x_ {1}}
\ fin {matriz}\ derecha]\ nonumber\]

Análisis de Estabilidad

Para evaluar la estabilidad del controlador, se pueden examinar los valores propios del jacobiano en los sistemas linealizados de ODEs. En general, un valor propio (lambda) es la solución a la siguiente ecuación:

\[|\mathbf{J}-\lambda \mathbf{I}|=0 \nonumber \]

Utilizando una computadora para resolver dicha ecuación, se puede encontrar que los valores propios de este sistema en particular son los siguientes:

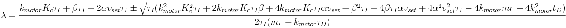
Para que el sistema sea estable, el componente real de todos los valores propios debe ser no positivo. La siguiente desigualdad debe ser cierta para un controlador estable:

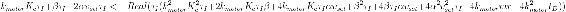
Para que el sistema no oscile, el componente imaginario de todos los valores propios debe ser cero. La siguiente desigualdad debe ser cierta para un controlador no oscilante:

\[\tau_I (k_{motor}^2 K_c^2 \tau_I+2 k_{motor} K_c \tau_I \beta+4 k_{motor} K_c \tau_I \alpha v_{set}+\beta^2 \tau_I+4 \beta \tau_I \alpha v_{set}+4 \alpha^2 v_{set}^2 \tau_I-4 k_{motor} mr-4 k_{motor}^2 t_D) \nonumber \]

Curiosamente, ninguno de estos criterios depende de la pendiente de la carretera (θ). Sin embargo, durante el análisis, se asumió que θ es constante. Para la mayoría de las carreteras, este no es el caso; θ es en realidad una función de la posición del vehículo. Para agregar este nivel adicional de detalle, es necesario revisar el sistema original de ODEs:

\[\frac{d v}{d t}=\frac{k_{\text {motor}} K_{c}\left(v_{\text {set}}, v\right)\left|k_{\text {motor}} x_{1}\right| k_{\text {motor}} C_{\text {offset}}}{k_{\text {motor}} l_{D}+\pi u r} \nonumber \]

\[\frac{d x_{1}}{d t}=v_{set}-v \nonumber \]

\[\frac{d s}{d t}=v \nonumber \]

\[\theta=f(s) \nonumber \]

Desafortunadamente para cualquier camino normal, la pendiente no es una función simple (o incluso explicar) de posición (es). Esto evita un análisis analítico en profundidad de la estabilidad. Sin embargo, para una carretera muy lisa con cambios de pendiente muy graduales, la estabilidad del controlador no debería verse afectada.

Ejemplo de Vehículo Eléctrico

Simulando el sistema también para que se examinen otras propiedades del controlador. En esta sección se presentan los resultados de la simulación de un vehículo eléctrico ficticio específico.

Parámetros

Para el vehículo eléctrico ficticio simulado en este análisis, se utilizaron los siguientes parámetros. Estos parámetros se basan aproximadamente en los parámetros que uno esperaría ver en un automóvil eléctrico típico.

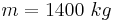
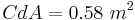
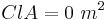
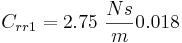
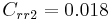
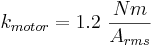
Parcelas de locus radicular

Usando los parámetros anteriores, se construyeron Gráficas de Locus Raíz del sistema para explorar numéricamente la estabilidad. Se utilizaron las siguientes constantes de controlador al construir las gráficas:

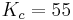
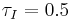
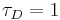
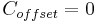
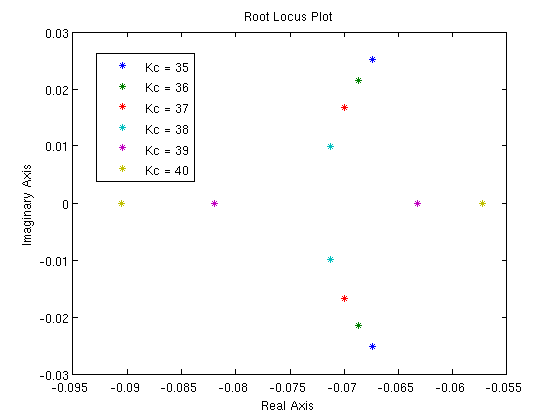
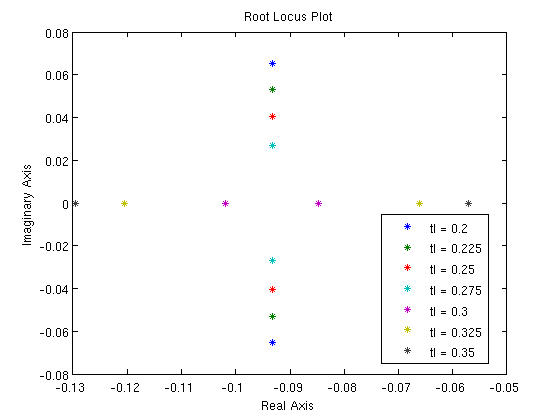
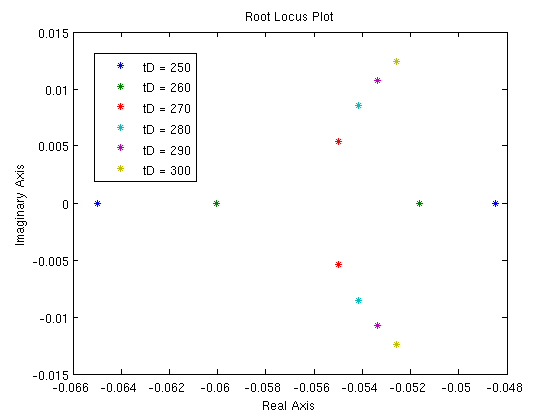
Estas gráficas de Locus Raíz muestran que el controlador con dichas constantes es estable y no oscila.

Retrato de Fase

También se construyó un retrato de fase del sistema con los siguientes parámetros:

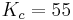
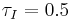
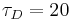
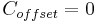
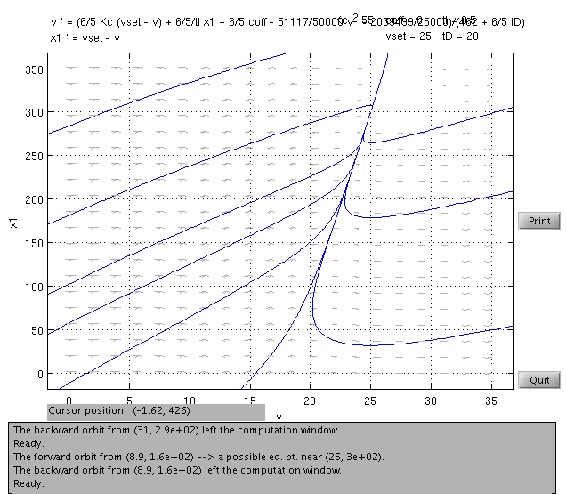
El retrato de fase muestra que el sistema es estable y no oscila, como predijeron las parcelas de Locus Raíz.

Simulación de conducción en terreno nivelado

El vehículo fue simulado a partir de 10 m/s y acelerando a 25 m/s vía control de crucero en terreno llano (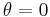). Para esta simulación se utilizaron las siguientes constantes:

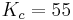
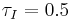
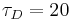
\[C_{o f f s e t}=146 \approx \frac{\alpha v_{s e t}^{2}+\beta v_{s e t}+\gamma(\theta=0)}{k_{m o t o r}} \nonumber \]

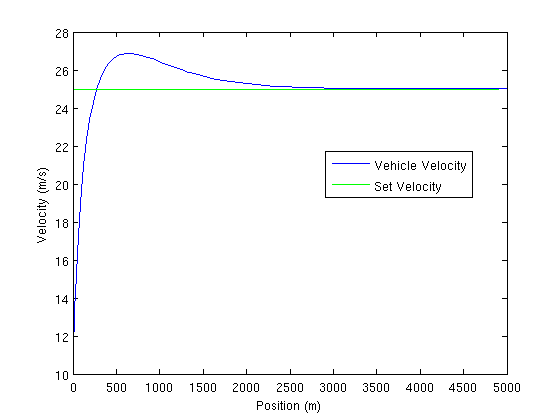
Curiosamente, esta gráfica muestra la oscilación, a pesar de las gráficas de Locus Raíz y diagramas de fase Es importante recordar, sin embargo, que la gráfica del Locus Raíz y los métodos de estabilidad implican linealizar el sistema. Es posible que el sistema linealizado no sea una buena aproximación del sistema.

También es importante recordar que este ejemplo en particular implica un gran cambio de punto de ajuste, que puede inducir oscilaciones en ciertos sistemas.

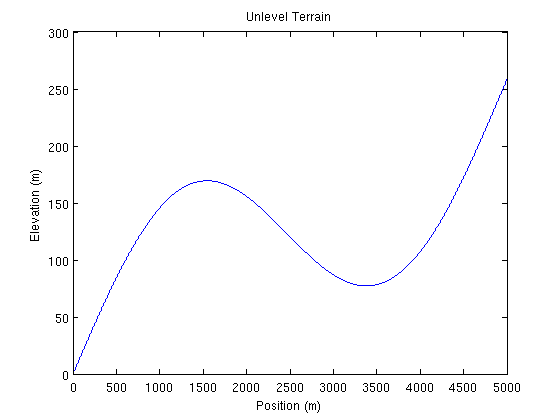
Simulación de conducción en terrenos no nivelados

Para explorar cómo se comporta el controlador en una carretera con pendiente distinta de cero, se construyó una ruta con cerros a partir de la siguiente ecuación, donde h es elevación y s es posición. :

\[h=100 \sin \left(\frac{s}{250 \pi}\right)+\frac{s}{2000} \nonumber \]

El vehículo fue simulado manejando dicha carretera comenzando con las siguientes condiciones iniciales y constantes del controlador:

Condiciones Iniciales

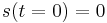
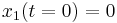
Constantes del controlador

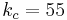
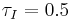
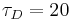
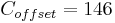
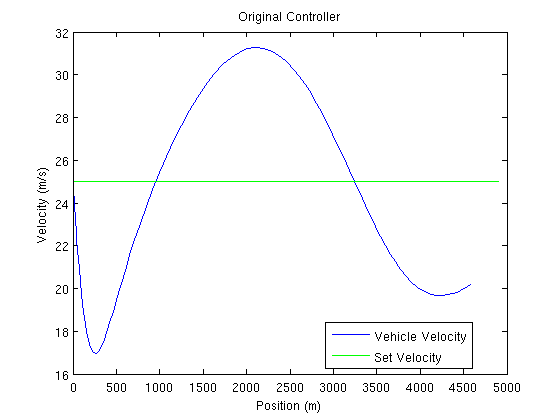
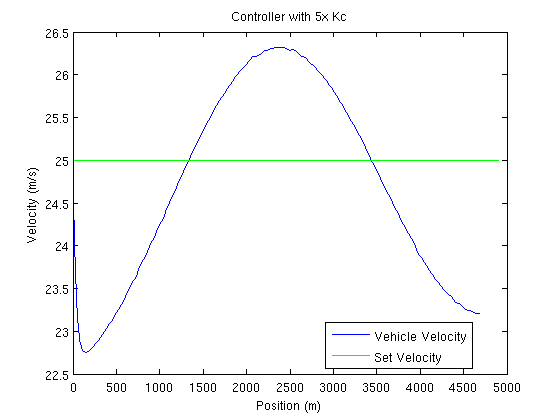
La sintonización del controlador de corriente es inadecuada para esta carretera. Existen variaciones grandes en la velocidad. Para reducir esta variación, la ganancia propartional K _c se incrementó en un factor de 5. A continuación se presentan los resultados:

Usando Optimization Toolbox en MATLAB, el controlador se optimizó minimizando la suma de los errores (diferencia entre la velocidad del vehículo y la velocidad establecida) en este segmento particular de carretera. A continuación se muestran las constantes optimizadas del controlador y una gráfica del perfil de velocidad:

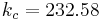
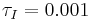
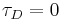
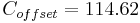
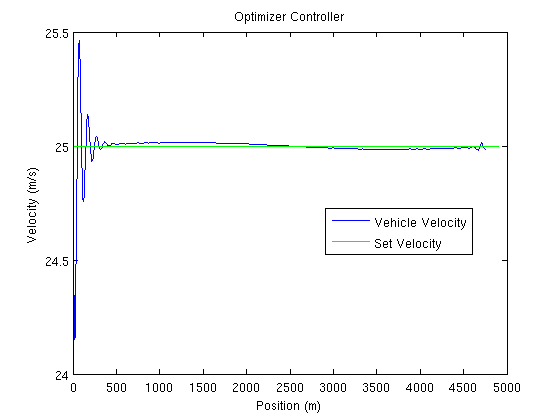
Este ejemplo muestra el poder de la optimización y el control predictivo del modelo.

Resumen

Este ejemplo demuestra lo siguiente:

1. Modelado de un sistema de ingeniería simple y no química.
2. Desarrollar un controlador PID para dicho sistema dinámico físico.
3. Manipular dicho sistema para desarrollar un sistema de ecuaciones diferenciales.
4. Encontrar punto (s) fijo (s) para dicho sistema.
5. Linealizar dicho sistema de ecuaciones diferenciales.
6. Encontrar los valores propios de dicho sistema linealizado.
7. Construir parcelas de Locus Raíz para dicho sistema linealizado.
8. Construir un retrato de fase para dicho sistema dinámico.
9. Simular dicho sistema dinámico bajo diversas condiciones.
10. Demostrar la idea de control predictivo del modelo optimizando dicho controlador bajo un escenario específico.