6.9: Control de Glucosa en Sangre en Pacientes Diabéticos

Última actualización
Guardar como PDF

Page ID: 85623

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Antecedentes de por qué el control de insulina es importante para los pacientes diabéticos

La diabetes mellitus es una enfermedad del sistema endocrino donde el cuerpo no puede controlar los niveles de glucosa en sangre. Hay dos clasificaciones generales de la diabetes:

Tipo I (también conocida como diabetes juvenil)

La predisposición genética y/o un ataque autoinmune destruye las células T del páncreas
El cuerpo no puede producir insulina para regular la glucosa en sangre

Tipo II

La forma más común de diabetes y ha alcanzado el estado epidémico en Estados Unidos
Generalmente causado por el estilo de vida
La obesidad reduce la capacidad de respuesta del cuerpo a la insulina

El tratamiento para ambos tipos de diabetes puede incluir ejercicio, dieta, medicamentos orales o inyecciones de insulina. La mayoría de los diabéticos dependientes de insulina siguen un plan de manejo que requiere pruebas frecuentes de los niveles de glucosa en sangre y luego la inyección de una dosis prescrita de insulina basada en el nivel de glucosa en sangre. Sin embargo, la desventaja de este método de tratamiento es que no existe un control predictivo. Si los niveles de glucosa en sangre están bajando y se administra insulina, puede ocurrir un episodio hipoglucémico. Los recientes avances biomédicos han dado como resultado dispositivos de monitoreo continuo de glucosa en sangre, así como bombas de insulina. El monitoreo continuo permite un control más fino de la glucosa en sangre y puede ayudar a predecir las fluctuaciones en el nivel de glucosa en sangre. Las bombas de insulina reemplazan la necesidad de administrar inyecciones de insulina inyectando automáticamente una dosis prescrita, sin embargo, requiere la entrada del nivel de glucosa en sangre del paciente. En el futuro, las bombas de insulina y los monitores continuos de glucosa en sangre pueden integrarse formando un sistema de control de circuito cerrado que puede reemplazar el propio sistema de control defectuoso del cuerpo.

Figura 1: Esquema de Control de Infusión de Insulina

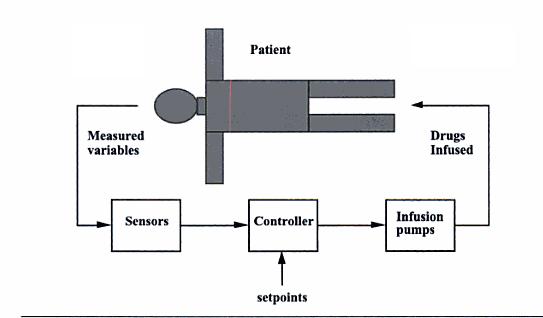
Modelo matemático para un sistema de administración de insulina de circuito cerrado

El siguiente conjunto de ecuaciones diferenciales se conoce como el “modelo mínimo” de Bergman:

\[\frac{d G}{d t}=-p_{1} G-X\left(G-G_{b}\right)+\frac{G_{m e a l}}{V_{1}} \nonumber \]

\[\frac{d X}{d t}=-p_{2} X+p_{3} I \nonumber \]

\[\frac{d I}{d t}=-n\left(I+I_{b}\right)+\frac{U}{V_{1}} \nonumber \]

donde:

G = variable de desviación para la concentración de glucosa en sangre
X = variable de desviación para la concentración de insulina en un compartimento “remoto”
I = variable de desviación para la concentración de insulina en sangre
G _comida = un aporte de alteración de la comida en la glucosa
U = la velocidad de infusión de insulina de manipulación
G _b = valor en estado estacionario de la concentración de glucosa en sangre
I _b = valor en estado estacionario de la concentración de insulina en sangre

Los parámetros sanguíneos incluyen p ₁, p ₂, p ₃, n, V ₁ (volumen sanguíneo). Estos son específicos del espécimen de sangre y deben estar predeterminados.

Se puede utilizar un modelo de espacio de estado lineal para expresar las ecuaciones de Bergman vistas arriba. La forma general para un modelo de espacio de estado se puede ver a continuación:

\ [\ left [\ begin {array} {c}
\ dot {x} _ {1}\
\\ vdots\
\ dot {x} _ {n}
\ end {array}\ right] =\ left [\ begin {array} {ccc}
a_ {11} &\ cdots & a_ {1 n}\
\ vdots &\ ddots &\ vdots\\
a_ {n} &\ cdots & a_ { n n}
\ end {array}\ derecha]\ left [\ begin {array} {c}
x_ {1}\
\ vdots\\
x_ {n}
\ end {array}\ right] +\ left [\ begin {array} {ccc}
b_ {11} &\ cdots & b_ {1 m}\
\ vdots &\ ddots &\ vdots\\
b_ {n 1} &\ cdots & b_ {n m}
\ end {array}\ derecha]\ izquierda [\ begin {array} {c}
u_ {1}\
\ vdots\\
u_ {m}
\ end {array}\ derecha]\ nonumber\]

\ [\ left [\ begin {array} {c}
y_ {1}\\
\ vdots\\
y_ {r}
\ end {array}\ right] =\ left [\ begin {array} {ccc}
c_ {11} &\ cdots & c_ {1 n}\\ vdots &
\ ddots &\ vdots &\ vdots\\
c_ {r 1} &\ cdots &\ c_ {r n}
\ end {array}\ derecha]\ left [\ begin {array} {c}
x_ {1}\\
\ vdots\\
x_ {n}
\ end {array}\ right] +\ left [\ begin {array} {ccc}
d_ {11} &\ cdots & d_ {1 m}\\
\ vdots &\ ddots &\ vdots\\
d_ {r 1} &\ cdots & d_ {r m}
\ end {array}\ right]\ left [\ begin {array} {c}
u_ {1}\
\ vdots\\
u_ {m}
\ end {array}\ derecha]\ nonumber\]

En general:

\[\dot{x}=A x+B u \nonumber \]

\[y=C x+D u \nonumber \]

donde:

x = estados
u = entradas
y = salidas

\ [A=\ left [\ begin {array} {ccc}
-p_ {1} & -G_ {b} & 0\\
0 & -P_ {2} & P_ {3}\\
0 & 0 & -n
\ end {array}\ derecha]\ nonumber\]

\ [B=\ izquierda [\ begin {array} {ll}
0 &\ frac {1} {V_ {1}}\\
0 & 0\
\ frac {1} {V_ {1}} & 0
\ end {array}\ derecha]\ nonumber\]

\ [C=\ left [\ begin {array} {lll}
1 & 0 & 0
\ end {array}\ right]\ nonumber\]

\ [D=\ izquierda [\ begin {array} {l}
0\\
0
\ end {array}\ derecha]\ nonumber\]

Usando esta fórmula general, podemos deconstruir las ecuaciones de Bergman como un modelo lineal de espacio de estado. La primera entrada es la infusión de insulina y la segunda entrada representa la alteración de la glucosa de la comida.

Primera entrada:

\ [\ left [\ begin {array} {c}
\ dot {G}
\\ dot {X}\
\ dot {I}
\ end {array}\ right] =\ left [\ begin {array} {ccc}
-p_ {1} & -G_ {b} &
0\\ 0 & -P_ {2} & P_ {3}\\
0 & -n
\ end matriz}\ derecha]\ left [\ begin {array} {c}
G\\
X\\
I
\ end {array}\ right] +\ left [\ begin {array} {cc}
0 &\ frac {1} {V_ {1}}\\
0 & 0\
\ frac {1} {V_ {1}} & 0
\ end {array}\ derecha]\ izquierda [\ begin {array} l }
u_ {1}\\
u_ {2}
\ end {array}\ derecha]\ nonumber\]

donde

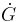$\ punto {G}$ = concentración diferencial de glucosa en sangre
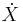$\ punto {X}$ = concentración diferencial de insulina en un compartimento “remoto”
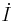$\ punto {I}$ = concentración diferencial de insulina en sangre

Segunda entrada:

\ [y=\ left [\ begin {array} {lll}
1 & 0 & 0
\ end {array}\ right] G+\ left [\ begin {array} {ll}
0 & 0
\ end {array}\ right]\ left [\ begin {array} {l}
u_ {1}\\
u_ {2}
\ end {array}\ derecha]\ nonumber\]

donde

\ [\ left [\ begin {array} {l}
u_ {1}\\
u_ {2}
\ end {array}\ right] =\ left [\ begin {array} {c}
U-U_ {b}\\
G_ {m e a l} -0
\ end {array}\ right]\ nonumber\]

Ejemplo de conjunto de parámetros

Gb = 4.5 mmol/litro
Ib = 4.5 MU/litro
V1 = 12 litros
p1 = 0/min
p2 = 0.025/min
p3 = 0.0000013 MU/Litro
n = 5/54 min-1

Es importante realizar un seguimiento de las unidades al usar estos parámetros. Las concentraciones enumeradas anteriormente están en mmol/litro, pero la alteración de la glucosa tiene unidades de gramos. Por lo tanto, es necesario que apliquemos un factor de conversión de 5.5556 mmol/gramos al término de la _comida G. Usando estas variables se puede resolver para los estados de equilibrio, y calcular la velocidad de infusión basal de insulina (Ub) tal que sea igual a 16.1667 mU/min. Para estos parámetros, el modelo de espacio de estado resultante es

\ [A=\ left [\ begin {array} {ccc}
0 & -4.5 & 0\\
0 & -0.025 & 0.000013\\
0 & 0 &\ frac {-5} {54}
\ end {array}\ derecha]\ nonumber\]

\ [B=\ left [\ begin {array} {cc}
0 & 0.4630\\
0 & 0\\
\ frac {1} {12} & 0
\ end {array}\ derecha]\ nonumber\]

Es práctica común en Estados Unidos describir la concentración de glucosa en unidades de mg/decilitro a diferencia de mmol/litro. Para ello, las unidades se convertirán de mmol/litro a mg/decilitro. El peso molecular de la glucosa es de 180g/mol, y por lo tanto uno es necesario multiplicar el estado de glucosa (mmol/litro) por 18, de manera que la salida de glucosa medida obtenida sea en unidades de mg/decilitro. La siguiente relación estado-salida manejará eso:

\ [C=\ left [\ begin {array} {lll}
18 & 0 & 0
\ end {array}\ right]\ nonumber\]

\ [D=\ left [\ begin {array} {ll}
0 & 0
\ end {array}\ derecha]\ nonumber\]

A través de las transformadas de Laplace se encontrará que la función de transferencia de procesos es:

\[G_{p}(s)=\frac{-3.79}{(40 s+1)(10.8 s+1) s} \nonumber \]

La función de transferencia de perturbaciones debido a la cancelación de polos/cero es simplemente:

\[G_{d}(s)=\frac{8.334}{s} \nonumber \]

Sin embargo, en realidad la glucosa no ingresa directamente al torrente sanguíneo. Hay un “tiempo de retraso” asociado con el procesamiento de la glucosa en el intestino. Primero debe procesarse aquí antes de ingresar a la sangre. Sin embargo, se puede modelar como una función de primer orden, con una constante de tiempo de 20 minutos. Esto modifica la ecuación anterior para la función de transferencia de perturbaciones para incluir el retraso en el intestino de tal manera que:

\[G_{d}(s)=\frac{8.334}{s(20 s+1)} \nonumber \]

Desempeño de control deseado

La concentración de glucosa en estado estacionario de 4.5 mmol/litro corresponde a la concentración de glucosa de 81 mg/decilitro. Un paciente diabético, para mantenerse saludable, debe mantener su concentración de glucosa en sangre por encima de 70 mg\ decilitro. Si la concentración de glucosa en sangre cae por debajo de 70 mg/decilitro es probable que el paciente se desmaye, ya que este es un síntoma muy típico de hipoglucemia a corto plazo. La velocidad de infusión de insulina (entrada manipulada) no puede caer por debajo de 0, y esta restricción debe establecerse en simulaciones. Se pueden utilizar numerosas estrategias de control diferentes. La ecuación dada para la función de proceso anterior se puede simplificar hasta la siguiente forma y se puede usar un controlador PD o PID.

\[G_{p}(s)=\frac{k_{p}}{\left(\tau_{p}+1\right) s} \nonumber \]

Un diabético sabrá cuándo está consumiendo una comida, y por lo tanto cuándo su concentración de glucosa en sangre puede subir. Por lo tanto, se puede desear un sistema de control de alimentación directa.

Referencias

Bechette, B. W. Control de Procesos: Modelado, Diseño y Simulación New Jersey: Prentice Hall, 2003. pp 81-83, 694-697.

Colaboradores y Atribuciones

Escrito por: Robbert Appel, Jessica Rilly, Jordan Talia