7.5: Laplace transforma

Última actualización
Guardar como PDF

Page ID: 85392

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Introducción

Laplace Transformada se utiliza frecuentemente en la determinación de soluciones de una amplia clase de ecuaciones differenciales parciales. Al igual que otras transformaciones, las transformaciones de Laplace se utilizan para determinar soluciones particulares. Al resolver ecuaciones diferenciales parciales, las soluciones generales son difíciles, si no imposibles, de obtener. Así, las técnicas de transformación a veces ofrecen una herramienta útil para lograr soluciones particulares. La transformada de Laplace está estrechamente relacionada con la transformada compleja de Fourier, por lo que la fórmula integral de Fourier se puede utilizar para definir la transformada de Laplace y su inversa [3]. Las transformaciones integrales son una de las muchas herramientas que son muy útiles para resolver ecuaciones diferenciales lineales [1]. Una transformación integral es una relación de la forma:

\[F(s)=\int_{a}^{b} K(s, t) f(t) d t \nonumber \]

donde$K(s, t)$ está el núcleo de la transformación

La relación dada anteriormente transforma la función f en otra función F, que se llama la transformada de f. La idea general al usar una transformación integral para resolver una ecuación diferencial es la siguiente:

Usar la relación para transformar un problema para una función desconocida f en un problema más simple para F
Resuelve este problema más sencillo para encontrar F
Recuperar la función deseada f de su transformada F

Se sabe que varias transformaciones integrales son útiles en las matemáticas aplicadas, pero en este capítulo solo consideramos la transformación de Laplace. Esta transformación se define de la siguiente manera Let f (t) be given for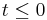 $\ leq 0$ . Entonces la transformada de Laplace de f, que denotaremos por 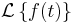$mathcal {L}\ izquierda\ {f (t)\ derecha\}$ , se define por la ecuación:

\[\mathcal{L}\{f(t)\}=\int_{0}^{\infty} e^{-s t} f(t) d t \nonumber \]

Siempre que esta integral impropia converja. La transformación de Laplace hace uso del núcleo K (s, t) = e ⁻ (st). Dado que las soluciones de ecuaciones diferenciales lineales con coeficientes constantes se basan en la función exponencial, la transformada de Laplace es particularmente útil para tales ecuaciones.

Tabla 1 - Tabla de Transformadas de Laplace

capaz 5 3 Un solo lado Laplace Transforms.jpg

Problemas de ejemplo

Funciones elementales usando transformaciones de Laplace

Ejemplo 1. Dado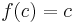 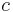$(c) =c\,\!$ , $\,\!$ es una constante

\[\\mathcal{L}[c] =\int_0^{\infty}e^{-st} c\,dt \,\! \nonumber \]

$=\ izquierda [{-\ frac {c e^ {-st}} {s}}\ derecha] _ {0} ^ {\ infty}$

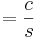
$=\ frac {c} {s}$

Ejemplo 2. Dado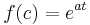 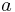$f (c) =e^ {at}\,\!$ , $a\,\!$ es una constante

\[\\mathcal{L}[e^{at}]=\int_0^{\infty}e^{-st} e^{at}\,dt\,\! \nonumber \]

$=\ izquierda [{-\ frac {e^ {- (s-a) t}} {(s-a)}}\ derecha] _ {0} ^ {\ infty}$

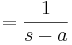$=\ frac {1} {s-a}$ , donde $s\ ge a\,\!$

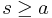
Ejemplo 3. Dado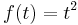 $f (t) =t^ {2}\,\!$ , Entonces

\[\mathcal{L}\left[t^{2}\right]=\int_{0}^{\infty} e^{-s t} t^{2} d t \nonumber \]

Integración por rendimientos de piezas

\[=\left[-\frac{t^{2} e^{-s t}}{s}\right]_{0}^{\infty}+\int_{0}^{\infty} \frac{e^{-s t}}{s} 2 t d t \nonumber \]

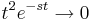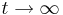Ya que $t^ {2} e^ {-st}\ a 0\,\!$ como $t\ a {\ infty}\,\!$ , tenemos

\[\\mathcal{L}[t^{2}]={\frac{2}{s}} \left [ {-\frac{e^{-st}}{s}}t \right ]_{0}^{\infty}+{\frac{2}{s}} \int_0^{\infty} {\frac{e^{-st}}{s}} \,dt \,\! \nonumber \]

\[ \begin{align*} \mathcal{L}\left[t^{2}\right]=\frac{2}{s}\left[-\frac{e^{-s t}}{s} t\right]_{0}^{\infty}+\frac{2}{s} \int_{0}^{\infty} \frac{e^{-s t}}{s} d t \\[4pt] &= \frac{2}{s^{3}} \end{align*} \nonumber \]

Ejemplo 4. Dado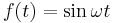 $f (t) =\ sin\ omega t\,\!$ . Entonces

\[F(s)=\mathcal{L}[\sin \omega t]=\int_{0}^{\infty} e^{-s t} \sin \omega t d t \nonumber \]

$=\ izquierda [- {\ frac {e^ {-st}} {s}}\ sin\ omega t\ derecha] _ {0} ^ {\ infty} +\ int_0^ {\ infty} {\ infty} {\ frac {e^ {-st}} {s}}\ omega\ cos\ omega t\, dt\,\!$

$= {\ frac {\ omega} {s}}\ izquierda [- {\ frac {e^ {-st}} {s}}\ cos\ omega t\ derecha] _ {0} ^ {\ infty} - {\ frac {\ omega} {s}}\ int_0^ {\ infty} {\ frac {e^ {-st}} {s}\ omega\ sin\ omega t\, dt\,\!$

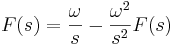
$F (s) = {\ frac {\ omega} {s}} - {\ frac {\ omega^ {2}} {s^ {2}} F (s)\,\!$

Así, resolviendo para$F(s)$, obtenemos

\[\mathcal{L}[\sin \omega t]=\frac{\omega}{\left(s^{2}+\omega^{2}\right)} \nonumber \]

Ejemplo en clase usando transformaciones de Laplace

Resolviendo una ecuación diferencial:

\[\frac{d y(t)}{d t}=-a y(t) \nonumber \]

Reordenando la ecuación a un lado, tenemos:

\[\frac{d y(t)}{d t}+a y(t)=0 \nonumber \]

A continuación, tomamos la transformación de Laplace

\[\left(s y(s)-y_{o}\right)+a y(s)=0 \nonumber \]

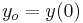donde $(s) = L [y (t)]\,\!$ y $y_o=y (0)\,\!$ Resolviendo para y (s), encontramos:

\[y(s)=\frac{y_{o}}{s+a} \nonumber \]

\[y(t)=\mathcal{L}^{-1}\{y(s)\}=\mathcal{L}^{-1}\left\{\frac{y_{o}}{s+a}\right\}=y_{o} e^{-a t} \nonumber \]

Referencias

William E. Boyce, Ecuaciones diferenciales elementales y problemas de valor límite (2005) Capítulo 6 pp 307-440.
Dr. Ali Muqaibel, EE207 Señales y Sistemas (2009) < http://tinyurl.com/ycq46qn >
Tyn Myint-U, Ecuaciones Diferenciales Parciales para Científicos e Ingenieros (2005) pp 337 -341.

Colaboradores y Atribuciones

Escrito por: Paul Rhee, Eric Chuang y David Mui