10.1: Encontrar puntos fijos en ODEs y modelos booleanos

Última actualización
Guardar como PDF

Page ID: 85563

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Autores: Nicole Blan, Jessica Nunn, Pamela Anne Roxas, Cynthia Sequerah
Administradores: Matthew Kerry Braxton-Andrew, Josh Katzenstein, Soo Kim, Karen Staubach

Introducción

Los ingenieros pueden obtener una mejor comprensión de los escenarios del mundo real mediante el uso de diversas técnicas de modelado para explicar el comportamiento de un sistema. Dos de estas técnicas son el modelado ODE y el modelado booleano. Una característica importante de un modelo ODE preciso son sus soluciones de punto fijo. Un punto fijo indica dónde se alcanza una condición de estado estacionario o equilibrio. Después de ubicar estos puntos fijos en un sistema, se puede determinar la estabilidad de cada punto fijo (ver Wikis posteriores). Esta información de estabilidad permite a los ingenieros determinar cómo funciona el sistema y sus respuestas a las condiciones futuras. También da información sobre cómo se debe controlar el proceso y les ayuda a elegir el tipo de control que mejor funcionará para lograrlo.

Concepto detrás de la búsqueda de punto fijo

Un punto fijo es una condición especial del sistema donde las variables o salidas medidas no cambian con el tiempo. En ingeniería química, llamamos a esto un estado estacionario. Los puntos fijos pueden ser estables o inestables. Si se introducen perturbaciones en un sistema en estado estacionario, pueden ocurrir dos resultados diferentes:

el sistema vuelve a esas condiciones originales (punto estable)
el sistema se desvía rápidamente de esas condiciones (punto inestable)

Los siguientes artículos wiki discutirán estos diferentes tipos de puntos fijos con más detalle. El foco de este artículo será simplemente encontrar puntos fijos, no clasificarlos. Discutiremos varios métodos para encontrar puntos fijos, dependiendo del tipo de modelo empleado.

Modelo ODE

Cuando un proceso o sistema es modelado por una ODE o un conjunto de ODEs, los puntos fijos se pueden encontrar utilizando diversas técnicas matemáticas, desde calcuaciones manuales básicas hasta programas matemáticos avanzados de computación. Independientemente del método utilizado, el principio básico sigue siendo el mismo: La ODE o conjunto de ODEs se establece en cero y las variables independientes se resuelven para. En los puntos donde las ecuaciones diferenciales son iguales a cero no se produce ningún cambio. Así, las soluciones encontradas al establecer las ODE iguales a cero representan los valores numéricos de variables independientes (es decir, temperatura, presión, concentración) en condiciones de estado estacionario. Si una sola ODE o conjunto de ODEs se vuelve demasiado complicado para resolverse a mano, se puede utilizar un programa matemático como Mathematica para encontrar puntos fijos. La última parte de este artículo se centra en cómo utilizar Mathematica para encontrar puntos fijos de sistemas complicados de ODEs.

Tenga en cuenta que en algunos casos puede que no exista un método analítico para encontrar un punto fijo. Este caso ocurre comúnmente cuando la solución a un punto fijo involucra un polinomio de alto grado u otra función matemática que no tiene una inversa analítica. En estos casos, todavía podemos encontrar puntos fijos numéricamente si tenemos los parámetros.

Modelo booleano

Un Modelo Booleano, como se explica en “Modelos Booleanos”, consiste en una serie de variables con dos estados: Verdadero (1) o Falso (0). Un punto fijo en un modelo booleano es una condición o conjunto de condiciones a las que converge el sistema modelado. Esto se ve más claramente dibujando diagramas de transición de estado.

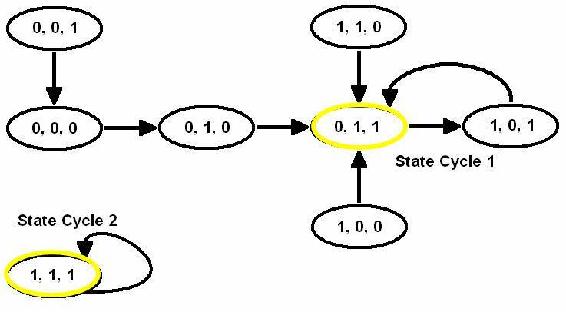
Diagrama de transición de estado a partir de modelos booleanos

Del diagrama de transición de estado anterior, podemos ver que hay dos puntos fijos en este sistema: 0,1,1 y 1,1,1. Comenzando en cualquier estado del diagrama y siguiendo las flechas, eventualmente se alcanzará uno de estos dos estados, lo que indica que el sistema tiende a lograr cualquiera de estos conjuntos de condiciones de operación. Si se introducen ligeras perturbaciones al sistema mientras está operando en uno de estos conjuntos de condiciones, volverá a 0,1,1 o 1,1,1. También se señalan en el diagrama de transición de estado los ciclos de estado. La diferencia entre un ciclo de estado y un punto fijo es que un ciclo de estado se refiere a todo el conjunto de funciones booleanas y puntos de transición que conducen a las condiciones de estado estacionario, mientras que un punto fijo se refiere simplemente al punto en un ciclo de estado donde se alcanzan las condiciones de estado estacionario (tales puntos son indicado por un círculo amarillo en el diagrama).

Encontrar Puntos Fijos: Cuatro Casos Posibles

Existen cuatro escenarios posibles al encontrar los puntos fijos de una ODE o sistema de ODEs:

Un punto fijo
Múltiples puntos fijos
Puntos fijos infinitos
Sin puntos fijos

Un punto fijo

El primer tipo de ODE tiene solo un punto fijo. Un ejemplo de tal ODE se encuentra en el Modelado de una Columna de Destilación. Se utiliza una ODE para modelar el balance energético en la enésima etapa de la columna de destilación:

\[\frac{d T_{n}}{d t}=\frac{1}{M_{W}}\left[L_{n-1} x_{n-1}-W x_{W}\right]\left[T_{n-1}-T_{n}\right]+\frac{q_{r}}{M_{W} c_{p}} \nonumber \]

Que también se puede escribir como:

\[\frac{d T_{n}}{d t}-\frac{1}{M_{W}} \left[ L_{n-1} x_{n-1}-W x_{W}\right]\left[T_{n-2}\right]+\frac{q_{r}}{M_{W} c_{p}}+\frac{1}{M_{W}}\left[L_{n-1} x_{n-1}-W x_{W}\right]\left[-T_{n}\right] \nonumber \]

Si se conocen las condiciones iniciales, es decir, T _{_n} _{_{− 1}}, L _{n − 1, x n} _{− 1}, la ecuación anterior se reduce a:

\[\frac{d T_{n}}{d t}=a+b T_{n} \nonumber \]

donde$a$ y$b$ son constantes ya que ahora se conocen todas las variables.

\[a=\frac{1}{M_{W}}\left[L_{n-1} x_{n-1}-W x_{W}\right]\left[T_{n-1}\right]+\frac{q_{r}}{M_{W} c_{p}} \nonumber \]

\[b=\frac{-1}{M_{W}}\left[L_{n-1} x_{n-1}-W x_{W}\right] \nonumber \]

Mediante el análisis de la ecuación

\[\frac{d T_{n}}{d t}=0=a+b T_{n} \nonumber \]

podemos deducir de inmediato eso en estado estacionario$T_n = - a/b$. Claramente, solo hay un punto fijo en este sistema, solo una temperatura de la columna de destilación que estará en condiciones de estado estacionario. Podemos usar Mathematica para resolver el punto fijo de este sistema y verificar nuestros resultados. En Mathematica, la función Solve [] se puede utilizar para resolver ecuaciones complicadas y sistemas de ecuaciones complicadas. Hay algunas reglas de formato simples que deben seguirse al usar Mathematica:

Escriba su ecuación y deje que el diferencial se llame una variable arbitraria (por ejemplo, T [t])
Escribe Resolver [T [t] ==0, T] y pulsa Mayús+Intro
Esto produce una salida contenida dentro de llaves

Por favor, lea la sección Resolver ODEs con Mathematica para obtener más información sobre sintaxis y funciones.

A continuación se muestra una muestra de cómo se ve el formato en Mathematica:

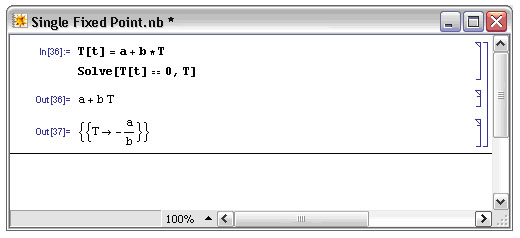
ingle fijo point.jpg

El arce se puede utilizar para visualizar un solo punto fijo. Dondequiera que la gráfica se intersecta, el eje x representa un punto fijo, porque la ODE es igual a cero en ese punto.

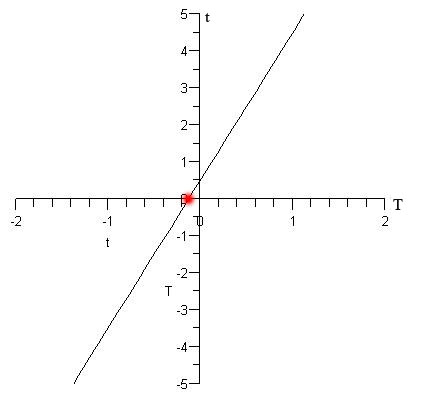
Se utilizó la siguiente sintaxis Maple para trazar la ODE: plot (0.5+4t, t=-2.. 2, T=0.. 5, color=negro);

La constante a = 0.5 y la constante b = 4 en el ejemplo anterior.

El gráfico resultante está abajo, el punto rojo indica en qué T se produce un punto fijo:

ne more.jpg

Resolviendo un solo punto fijo para una ODE y un controlador en Mathematica

Identificar qué tipo de controlador es (P, I, PI, o PID etc.)
Identifica tus ecuaciones de ODE (¿El controlador es una función de la ODE?)

Ejemplo: Resuelve para los puntos fijos dadas las tres ecuaciones diferenciales y los dos controladores (u1 y u2).

\[\left.\frac{d H}{d t}=(1 / A) (F(i n)-F_{out}\right)\right) \nonumber \]

\[\left.\frac{\left.d F_{in} \right)}{d t}=K(v 1)\left(u_{1}\right) \nonumber \]

\[\left.\frac{\left.d F_{out}\right)}{d t}=K_{(v2} \right)\left(u_{2}\right) H \nonumber \]

Donde H es el nivel en el tanque,$F_{in}$ es el flujo de entrada,$F_{out}$ el flujo de salida,$u_1$ y$u_2$ son las señales a las válvulas$v_1$ y$v_2$. $Kv1$y$Kv2$ son ganancias de válvula (se supone que son lineales en este caso, aunque esto no tiene por qué serlo). Tenga en cuenta que el flujo de salida también depende de la profundidad del fluido en el tanque.

A continuación parametriza su modelo a partir de datos experimentales para encontrar valores para las constantes:

A=2.5 metros cuadrados

K_ (v1) =0.046 metros cubo/ (minuto mA)

K_ (v2) =0.017 metros cuadrados/ (minuto mA)

A continuación desea agregar:

Un controlador PID completo para regular Fout a través de FC1 conectado a v2.
Un controlador solo P para regular H a través de LC1 conectado a v1.

Para este sistema se desea mantener el nivel del tanque a 3 metros y el flujo de salida (Fset) a 0.4 m3 /minuto. El siguiente código de Mathematica debería tener el siguiente aspecto:

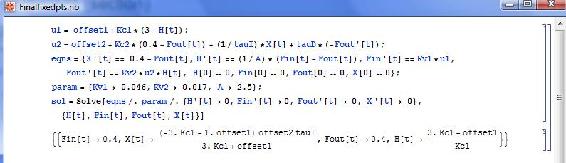
Múltiples Puntos Fijos

Múltiples puntos fijos para una ODE o sistema de ODEs indican que existen varios estados estables para un proceso, lo cual es una situación bastante común en la cinética del reactor y otras aplicaciones. Cuando existen múltiples puntos fijos, las condiciones óptimas de estado estacionario se eligen en función de la estabilidad del punto fijo y las condiciones de operación deseadas del sistema.

A continuación se muestra un ejemplo de un sistema de ODEs con múltiples puntos fijos:

\[\frac{d C_{A}}{d t}=14 C_{A}-2 C_{A}^{2}-C_{A} C_{B} \nonumber \]

\[\frac{d C_{B}}{d t}=16 C_{B}-2 C_{B}^{2}-C_{A} C_{B} \nonumber \]

El sistema anterior de ODEs se puede ingresar en Mathematica con la siguiente sintaxis:

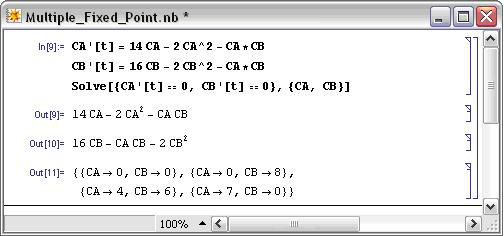
ultiple Fijo Points.jpg

Este sistema en particular tiene cuatro puntos fijos. Maple se puede utilizar para visualizar los puntos fijos usando la siguiente sintaxis:

con (parcelas):

diagrama de campo ([14*x-2*x^2-x*y,16*y-2*y^2-x*y], x=0.. 10, y=0.. 10, campofuerza=log);

La primera línea inicializa el paquete de trazado dentro de Maple que permite trazar campos vectoriales. La segunda línea utiliza el comando “fieldplot” e introduce las dos ODEs que conforman el sistema. Las escalas de los ejes x e y se establecen en un rango de 0 a 10. El comando fieldstrength se utiliza principalmente con fines visuales, de manera que la dirección de las flechas se vuelve más evidente. A continuación se muestra la gráfica resultante:

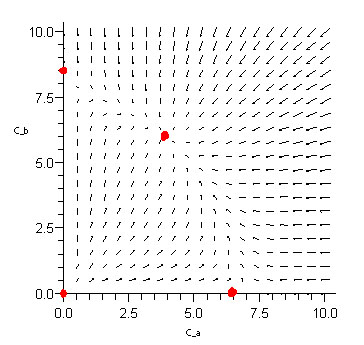
ultiple Puntos Fijos Graph.jpg

Los puntos rojos indican los puntos fijos del sistema. En la parcela, estos puntos son donde convergen o divergen todas las flechas circundantes. Las flechas convergentes indican un punto fijo estable, en este ejemplo el punto en (4,6) es un punto fijo estable. Las flechas divergentes indican un punto fijo inestable, en este ejemplo (0,0), (0,8) y (7,0) son puntos fijos inestables.

Puntos Fijos Infinitos

Un ejemplo de una ODE con puntos fijos infinitos es una ODE oscilante como:

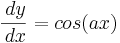
$frac {\, dy} {\, dx} =cos (hacha)$

donde a es una constante.

Usando Mathematica para resolver los puntos fijos mediante el ajuste

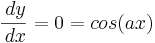
$frac {\, dy} {\, dx} =0=cos (hacha)$

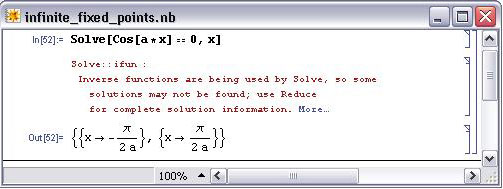
nfinitte fijo points.JPG

Si hace clic en el enlace “Más” en Mathematica básicamente indicará que existen otras soluciones posibles de acuerdo con la sección de Ayuda que se muestra a continuación:

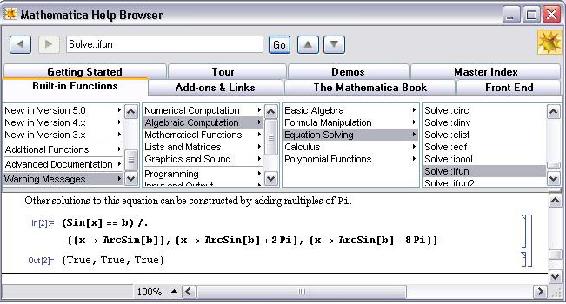
La sintaxis de Maple utilizada para graficar la ecuación diferencial resuelta es:

parcela (cos (3t), t=0.. 10, T=-1.. 1, color=negro);

La constante a = 3 en este caso.

Los puntos fijos infinitos se pueden ver en la gráfica de abajo, donde cada vez que la función cruza el eje x, tenemos un punto fijo:

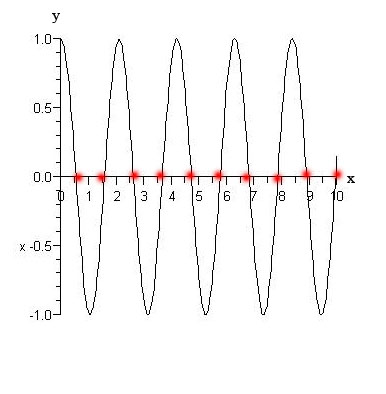
Sin puntos fijos

El cuarto tipo de ODE no contiene puntos fijos. Esto ocurre cuando una determinada variable (como la temperatura o la presión) no tiene ningún efecto sobre un sistema independientemente de cómo cambie. Generalmente, los sistemas con este tipo de comportamiento deben evitarse porque son difíciles de controlar ya que siempre están cambiando.

Esto puede modelarse mediante líneas verticales u horizontales debido a que no se encuentran puntos fijos estableciendo la línea igual a cero. Una ODE se utiliza para modelar una línea mantenida constante a:

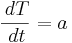
$frac {\, dT} {\, dt} =a$

Donde, a puede ser cualquier constante excepto 0.

Intuitivamente, tratar de encontrar un punto fijo en este sistema no es posible, porque una constante como 3 nunca puede ser igual a cero. Resolver esta ODE no es posible ni siquiera analizando el sistema. Por lo tanto, al ingresar esto en Mathematica, rinde {}. La notación {} significa que no hay puntos fijos dentro del sistema. La siguiente imagen es cómo Mathematica resuelve la ODE.

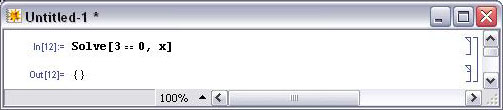
o Fijo Points.jpg

Al usar Maple (versión 10), se puede ver visualmente la falta de puntos fijos usando la siguiente sintaxis:

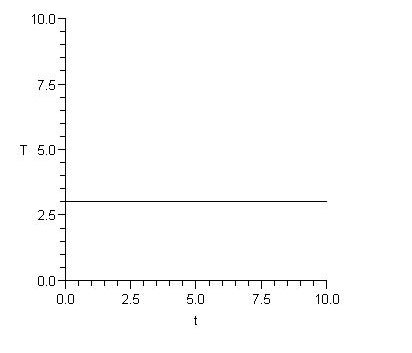
parcela (3, t = 0.. 10, T = 0.. 10, color = negro);

La constante a = 3 en el caso anterior.

Esta imagen muestra que la línea es horizontal y nunca cruza el eje x, lo que indica una falta de puntos fijos.

Resumen

Un punto fijo es una condición del sistema donde las variables o salidas medidas no cambian con el tiempo. Estos puntos pueden ser estables o inestables; consulte Usar valores propios para evaluar la estabilidad para una introducción a un método común para determinar la estabilidad de los puntos fijos.

Existen cuatro casos posibles a la hora de determinar puntos fijos para un sistema descrito por ODEs:

Un punto fijo
Múltiples puntos fijos
Puntos fijos de Infitita
Sin puntos fijos

Existen métodos descritos anteriormente para usar Mathematica o Maple para resolver los puntos fijos en cada caso. Los puntos fijos también se pueden determinar para un modelo booleano.

Conocer los puntos fijos de un sistema es muy importante a la hora de diseñar una arquitectura de control para el sistema. Estas son las condiciones de operación que el sistema exhibirá en estado estacionario. Los controladores pueden tener influencia en los puntos fijos, por lo que se debe realizar un análisis exhaustivo de los puntos fijos utilizando ecuaciones que describan el sistema y los controladores antes de la implementación del esquema de control.

Ejemplo 1: Manipulación de un Sistema de Ecuaciones

Recordemos el sistema de ejemplo de ODEs utilizado en la Sección de Puntos Fijos Múltiples:

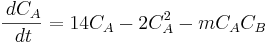
$frac {\, DC_a} {\, dt} = 14c_a-2c_a^2-mc_ac_b$

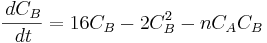
$frac {\, dc_b} {\, dt} = 16c_b-2c_b^2-nc_ac_b$

Encuentra cómo cambian los puntos fijos cuando m = 2 y n = 3.

Solución

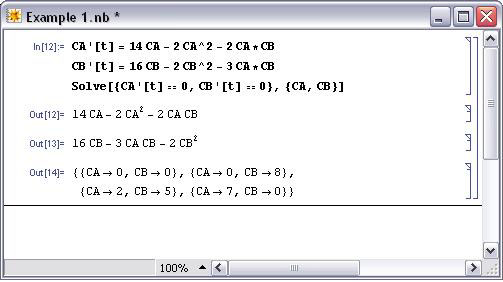
xample 1 problema solution.jpg

Ejemplo 2: Sistema de ODEs

Se le solicita estimar el punto (s) fijo (s) de un intercambiador de calor en su planta. Los puntos fijos corresponden a las temperaturas de sus fluidos del lado del tubo (caliente) y del lado de la carcasa (frío) respectivamente, T _t_, _out y T _s_, _out. Descuidar la pérdida de calor a la zona circundante es decir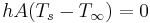 $A (T_ {s} - T_ {\ infty}) =0$ .

Dadas las dos ODE principales utilizadas para modelar un intercambiador de calor, utilice Mathematica para resolver los puntos fijos del sistema en términos de las variables conocidas.

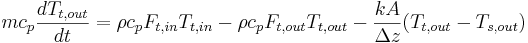$mc_ {p}\ frac {dt_ {t, out}} {dt} =\ rho c_ {p} F_ {t, in} T_ {t, in} -\ rho c_ {p} F_ {t, out} T_ {t, out} -\ frac {kA} {\ Delta z} (T_ {t, out} - T_ {s, out})$ (ecuación 1)

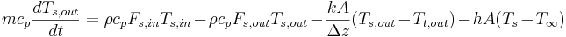$mc_ {p}\ frac {dt_ {s, out}} {dt} =\ rho c_ {p} F_ {s, in} T_ {s, in} -\ rho c_ {p} F_ {s, out} T_ {s, out} -\ frac {kA} {\ Delta z} (T_ {s, out} - T_ {t, out}) - hA (T_ {s} - T_ {\ infty})$ (ecuación 2)

Los valores para m, c _p, ρ, F _t_, _in, F _t_, _out, k, A, δ z y T _t _, _in, f _s_, _in, f _s_, _out, t _s_, _in se dan y fijo.

Consulte el artículo de Wiki sobre HeatExchangeModel para obtener una explicación detallada sobre el significado de las variables y la derivación de las ODE anteriores.

Pista: Agrupar todas las variables conocidas bajo una variable general

Solución

Simplifique las 2 ecuaciones a las ODE a continuación:

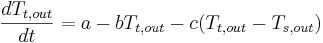$frac {dT_ {t, out}} {dt} =a-bt_ {t, out} -c (T_ {t, out} - T_ {s, out})$ (ecuación 1a)

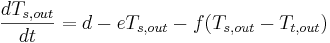$frac {dT_ {s, out}} {dt} =d-ET_ {s, out} -f (T_ {s, out} - T_ {t, out})$ (ecuación 2a)

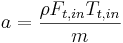
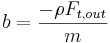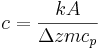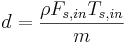
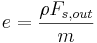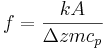
donde $=\ frac {\ rho F_ {t, in} T_ {t, in}} {m}$ $=\ frac {-\ rho F_ {t, fuera}} {m}$ , $=\ frac {kA} {\ Delta zmc_p}$ y $=\ frac {\ rho F_ {s, en} T_ {s, en}} {m}$ $=\ frac {\ rho F_ {s, fuera}} {m}$ , $=\ frac {kA} {\ Delta zmc_p}$

Escriba esta ecuación en Mathematica usando la sintaxis apropiada y use la función Solve [] para encontrar los puntos fijos.

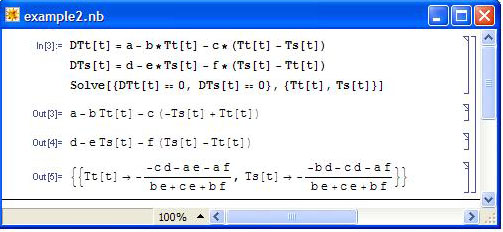
Hemos encontrado nuestro punto fijo. Simplemente conecte las variables definidas anteriormente para a, b, c, d, e, f y obtendrá las temperaturas en términos de los parámetros útiles.

Pregunta de opción múltiple 1

Las soluciones encontradas al establecer la ODE igual a cero representan:

a) Variables independientes no en condiciones de estado estacionario

b) variables dependientes no en condiciones de estado estacionario

c) Variables independientes en condiciones de estado estacionario

d) variables dependientes en condiciones de estado estacionario

Respuesta: C

Pregunta de opción múltiple 2

¿Cuántos puntos fijos hay cuando Mathematica resuelve la siguiente ecuación?

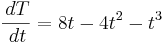
$frac {\, dT} {\, dt} = 8t-4t^2-t^3$

a) ninguno

b) 1

c) 2

d) 3

Respuesta: D

Rincón de Sage

Estabilidad de Puntos Fijos
video.google.com/googleplayer... 80917022362654

diapositivas para esta charla

Referencias

Edwards H., Penney D. (2003), Ecuaciones diferenciales: Computación y Modelado, Tercera Edición. Prentica-Salón. ISBN 0130673374
Strogatz, Steven H. (2001), Dinámica no lineal y caos: con aplicaciones a la física, biología, química e ingeniería, 1a edición. Addison-Wesley. ISBN 0738204536